2. Rappels de Logique
Pour construire une langue (par
exemple le français), on a besoin de 4 choses :
- un alphabet (a, b, ..., z, blanc, virgule, parenthèse ouvrante, ...)
- un procédé de formation des mots, qui est la concaténation
- un dictionnaire, qui permet de savoir que "chat" est français, alors que
"cat" ne l'est pas
- des règles de grammaire, qui permettent de savoir que "chattes" est
français, alors qu'il n'est pas dans le dictionnaire.
Pour construire un système formel, nous
aurons besoin de 4 choses analogues :
- un alphabet, ensemble de symboles pas nécessairement réduit à des
caratères
- un procédé de formation des expressions, pas nécessairement la
concaténation
- un ensemble d'axiomes, c'est-à-dire d'expressions obéissant aux
deux premiers points ci-dessus, et dont on décide arbitrairement qu'ils
appartiennent au système
- des règles de dérivation qui, à partir des axiomes, permettent de produire
des théorèmes (c'est-à-dire des expressions appartenant au système), et
peuvent ensuite s'appliquer aux théorèmes pour en produire d'autres
Considérons le système "peu" :
- alphabet = l'ensemble des trois symboles "p" , "e" , et "u"
- p.f.e. = concaténation
- axiome = upueuu
- règles :
- R1 : si une expression de la forme AeB est un théorème (où "A" désigne
n'importe quelle suite de "u", de "p", et de "e", et B de même), alors
l'expression uAeBu est aussi un théorème
- R2 : si une expression de la forme AeB est un théorème, alors
l'expression AueuB est aussi un théorème
Questions :
- Q1 = uupuueuuuu est-il un théorème?
- Q2 = upuueuuuu ?
- Q3 = upupueuuu ?
 Réponses
:
Réponses
:
- Q1, oui. Preuve? On développe l'arbre :
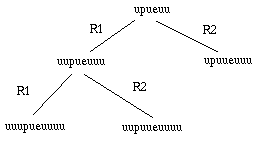
- Q2, non : il y a un nombre impair de "u", ce qui n'est pas possible
- Q3, non : il y a deux "p"
Pour démontrer qu'une expression est un
théorème, nous avons une procédure (développer l'arbre)
infaillible, qui répond en 2n/2, n étant la longueur de la
chaîne, donc en temps fini.
Par contre, pour démontrer qu'une
expression est un non-théorème, il nous faut "tricher". Dans les deux exemples
ci-dessus, nous avons fait de l'arithmétique, que faudrait-il faire sur un autre
exemple?
 Donc les notions de "être un
théorème" et de "être un non-théorème" ne sont pas symétriques.
Notre système "peu" est semi-décidable : nous avons une procédure qui répond
"oui" en temps fini, mais pas de procédure pour répondre "non".
Considérons le système :
Donc les notions de "être un
théorème" et de "être un non-théorème" ne sont pas symétriques.
Notre système "peu" est semi-décidable : nous avons une procédure qui répond
"oui" en temps fini, mais pas de procédure pour répondre "non".
Considérons le système :
- alphabet = l'ensemble des trois symboles "plus " , "egal " , et "un "
- p.f.e. = concaténation
- axiome = un plus un egal un un
- règles :
- R1 : si une expression de la forme A egal B est un théorème (où
"A" désigne n'importe quelle suite de "un ", de "plus ", et de "egal ", et B
de même), alors l'expression un A egal B un est aussi un théorème
- R2 : si une expression de la forme A egal B est un théorème,
alors l'expression A un egal un B est aussi un théorème
Questions :
- Q1 = un un plus un un egal un un un un est-il un théorème?
- Q2 = un plus un un egal un un un un ?
- Q3 = un plus un plus un egal un un un ?
Réponses : oui, non, et
non, car les deux systèmes sont isomorphes.
 Si nous remplaçons "plus " par "+", "egal " par
"=", et "un " par "1", l'axiome s'écrit : 1+1=2 , en base 1 (les chiffres
romains, concaténation = addition).
Si nous remplaçons "plus " par "+", "egal " par
"=", et "un " par "1", l'axiome s'écrit : 1+1=2 , en base 1 (les chiffres
romains, concaténation = addition).
R1 se lit : si A=B, alors 1+A=B+1
R2 :
si A=B, alors A+1=1+B
Q1 : 2+2=4 est un théorème Q2 : 1+2=4 est un
non-théorème Q3 : 1+1+1 ... est-un non-théorème !
Ce que nous venons de manipuler
n'est pas un système formel : le symbole "2" ne fait pas partie de l'alphabet.
Ce que nous venons de manipuler est l'interprétation du système
formel. "1+1+1=3", dans l'interprétation, est vrai, bien que ce
soit un non-théorème.
 Une
interprétation d'un S.F. n'est en général pas équivalente au S.F.,
c'est-à-dire que les notions de "être un théorème" et "être un non-théorème"
d'une part, et de "être vrai" et "être faux" d'autre part, peuvent ne pas se
recouvrir.
Une
interprétation d'un S.F. n'est en général pas équivalente au S.F.,
c'est-à-dire que les notions de "être un théorème" et "être un non-théorème"
d'une part, et de "être vrai" et "être faux" d'autre part, peuvent ne pas se
recouvrir.
Cependant, il ne faut pas rejeter l'interprétation :
souvenez-vous, si vous avez étudié un peu de Géométrie, la première fois qu'on
vous a demandé "démontrer que le triangle ABC est isocèle". Vous avez
soigneusement mesuré les deux cotés, et vous avez dit : "Oui, les deux cotés
sont égaux". Et l'enseignant vous a répondu : "NON! Ce n'est pas parce que c'est
vrai sur la figure que c'est un théorème". Mais vous n'avez pas pour autant
cessé de faire des figures pour résoudre les problèmes, parce qu'elles
guident le raisonnement. Nous y reviendrons.
Considérons un système formel quelconque,
et l'ensemble (qui peut être infini) des expressions qu'on peut engendrer dans
ce système en appliquant le procédé de formation des expressions. Nous pouvons
partitionner cet ensemble en : les expressions qui sont des théorèmes, et celles
qui sont des non-théorèmes. 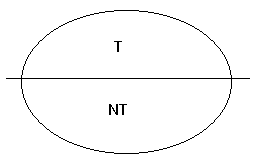
Nous pouvons également partitionner cet
ensemble en : ce qu'une procédure peut démontrer en temps fini, et ce qu'elle ne
peut pas : 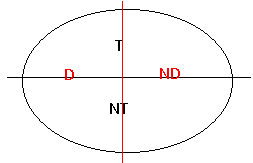
Si la partie ND est
vide, le système est dit décidable. Si la partie TND est vide, il est
semi-décidable. Si aucune partie n'est vide, il est indécidable.
Nous pouvons
par ailleurs partitionner l'ensemble en : les expressions dont l'interprétation
est "vrai", et celles dont l'interprétation est "faux" : 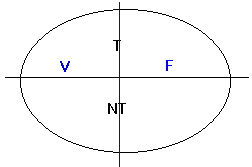
Si la partie TF n'est pas vide, nous dirons
que notre interprétation est sans intérêt. On montre en revanche que la partie
NTV n'est, en général, pas vide.
Lorsqu'une proposition "manifestement vraie"
ne peut être démontrée, on est donc en droit de se demander dans laquelle de ces
zones on se trouve. Un cas célèbre était la conjecture de Fermat, qui a tenu les
mathématiciens en échec pendant trois siècles : il n'existe pas d'entiers
positifs x, y et z, et d'entier n supérieur à 2, tels que
xn+yn=zn .
| alphabet |
distance.<.2km
distance.<.300km
aller.à.pied
prendre.le.train
prendre.l'avion
avoir.le.téléphone
aller.à.l'agence
téléphoner.à.l'agence
acheter.un.billet
durée.>.2.jours
être.fonctionnaire
(
)
non (négation)
^ (et, ou conjonction)
-> (implique)
|
procédé de
formation des
expressions |
expression <= symbole
expression <= ( expression )
expression <= non expression
expression <= expression1 ^ expression2
expression <= expression1 -> expression2
|
| axiomes |
R1 : distance.<.2km -> aller.à.pied
R2 : ((non distance.<.2km) ^ distance.<.300km) ->
prendre.le.train
R3 : (non distance.<.300km) -> prendre.l'avion
R4 : (acheter.un.billet ^ avoir.le.téléphone) ->
téléphoner.à.l'agence
R5 : (acheter.un.billet ^ (non avoir.le.téléphone)) ->
aller.à.l'agence
R6 : prendre.l'avion -> acheter.un.billet
R7 : (durée.>.2.jours ^ être.fonctionnaire) ->
(non prendre.l'avion)
F1 : (non distance.<.300km)
F2 : avoir.le.téléphone
|
règle de
dérivation |
Si A est un théorème, et si
A -> B est un théorème, alors
B est un théorème
Cette règle est connue sous le nom de "modus
ponens" |
Les Ri ont été obtenues de
l'"expert" par le processus de développement incrémental (cf. 3. 1.). C'est
la mémoire à long terme, ou base de connaissances du
système ; on ne les modifiera que si on y détecte une erreur.
Les
Fj représentent un problème qu'on va soumettre au système. C'est sa
mémoire à court terme, ou base de faits.
Ni la
BdC ni la BdF ne sont programmées : elles sont mises telles quelles dans le
système. Le seul programme est le moteur d'inférence, qui réifie
la règle de dérivation :
ça marche
tant que ça marche
ça ne marche pas
boucle sur les Ri
boucle sur les Fj
si Ri est de la forme "Fj -> Fk"
ajouter Fk à la BdF
ça marche
finsi
finboucle
finboucle
fintant
|
Traditionnellement, on représente le système par
la "tête de Mickey" : 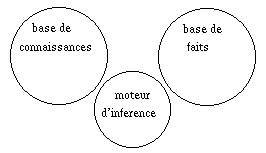
Lançons le système : ça ne marche pas
R1 et F1 : rien
R1 et F2 : rien
R2 et F1 : rien
R2 et F2 : rien
R3 et F1 : F3 (prendre.l'avion) et ça marche
R3 et F2 : rien
R3 et F3 : rien
...
R6 et F3 : F4 (acheter.un.billet) et ça marche
...
R7 et F4 : rien
ça ne marche pas
R1 et F1 : rien
R1 et F2 : rien
R1 et F3 : rien
R1 et F4 : rien
...
R4 et F4 et F2 : F5 (téléphoner.à.l'agence)
 NON! C'est vrai dans
l'interprétation, mais ce n'est pas un théorème du système formel ! Nous n'avons
pas écrit, et encore moins programmé :
NON! C'est vrai dans
l'interprétation, mais ce n'est pas un théorème du système formel ! Nous n'avons
pas écrit, et encore moins programmé :
règle de
dérivation |
Si A est un théorème, et si
B est un théorème, alors
A ^ B est un théorème
|
La distinction entre "et" et "^" n'est pas un
snobisme, pas plus que celle que nous faisons entre "si...alors..." et "->" .
Corrigeons :
ça marche
tant que ça marche
ça ne marche pas
boucle sur les Ri
boucle sur les Fj
si Ri est de la forme "Fj -> Fk"
ajouter Fk à la BdF
ça marche
sinon
boucle sur les Fl
si Ri est de la forme "Fj ^ Fl ->..."
ajouter Fm = (Fj ^ Fl) à la BdF
ça marche
finsi
finboucle
finsi
finboucle
finboucle
fintant
|
Relançons le système : ça ne marche pas
modus ponens avec R3 et F1 : F3 (prendre.l'avion) et ça marche
modus ponens avec R6 et F3 : F4 (acheter.un.billet) et ça marche
ça ne marche pas
règle du "et" avec F4 et F2 : F5 (acheter.un.billet ^ avoir.le.téléphone)
et ça marche
ça ne marche pas
modus ponens avec R4 et F5 : F6 (téléphoner.à.l'agence) et ça marche
ça ne marche pas
arrêt
 NON! C'est vrai en Logique,
mais pas en Informatique ! Notre programme va continuer à produire :
NON! C'est vrai en Logique,
mais pas en Informatique ! Notre programme va continuer à produire : modus ponens avec R3 et F1 : F7 (prendre.l'avion) et ça marche
...
Notre programme ne donne pas la solution en temps fini, car il boucle.
Pour éviter cela, nous marquons les Fj au fur et à mesure que nous
les utilisons :
ça marche
tant que ça marche
ça ne marche pas
boucle sur les Ri
boucle sur les Fj non marqués
si Ri est de la forme "Fj -> Fk"
ajouter Fk à la BdF
marquer Fj
ça marche
sinon
boucle sur les Fl
si Ri est de la forme "Fj ^ Fl ->..."
ajouter Fm = (Fj ^ Fl) à la BdF
marquer Fj
ça marche
finsi
finboucle
finsi
finboucle
finboucle
fintant
|
A présent, le programme est correct, et donne la
réponse en temps fini, quel que soit l'ordre dans lequel nous écrivons
les Ri et les Fj. Nous avons donc réalisé notre objectif :
nous pouvons exprimer nos connaissances sans les programmer.
Reprenons le même système, en
changeant un peu la base de faits :
| axiomes |
R1 : distance.<.2km -> aller.à.pied
R2 : ((non distance.<.2km) ^ distance.<.300km) ->
prendre.le.train
R3 : (non distance.<.300km) -> prendre.l'avion
R4 : (acheter.un.billet ^ avoir.le.téléphone) ->
téléphoner.à.l'agence
R5 : (acheter.un.billet ^ (non avoir.le.téléphone)) ->
aller.à.l'agence
R6 : prendre.l'avion -> acheter.un.billet
R7 : (durée.>.2.jours ^ être.fonctionnaire) ->
(non prendre.l'avion)
F1 : (non distance.<.300km)
F2 : avoir.le.téléphone
F3 : durée.>.2.jours
F4 : être.fonctionnaire
|
Lançons le système : modus ponens avec R3 et F1 : F5 (prendre.l'avion)
modus ponens avec R6 et F5 : F6 (acheter.un.billet)
règle du "et" avec F3 et F4 : F7 (durée.>.2.jours ^ être.fonctionnaire)
règle du "et" avec F4 et F2 : F5 (acheter.un.billet ^ avoir.le.téléphone)
modus ponens avec R4 et F5 : F6 (téléphoner.à.l'agence)
modus ponens avec R7 et F7 : F8 (non prendre.l'avion)
L'"expert" va s'insurger : notre système a déduit, d'une part, qu'il
fallait prendre l'avion (F5), et d'autre part qu'il ne fallait pas
(F8).
Alors, sous réserve d'un stockage des déductions, nous pouvons
interroger le système : Q : pourquoi F5?
R : modus ponens avec R3 et F1
Q : pourquoi F8 ?
R : modus ponens avec R7 et F7
Q : pourquoi F7?
R : ègle du "et" avec F3 et F4
Nous savons à présent que l'erreur provient d'une contradiction entre R3
et R7, que nous montrons à l'expert. Comment corriger? En supprimant R3, et en
le remplaçant par les bons axiomes, ceux qui traitent tous les cas. Où placer
les nouveaux axiomes? N'importe où.
La mise au point ne coute pas $4000,
parce que :
- le système s'explique, et nous permet de trouver rapidement la cause de
l'erreur
- la correction n'a pas à tenir compte du reste de la BdC
Dorénavant, nous appellerons "règles"
les axiomes de type Ri, c'est-à-dire les axiomes qui contiennent
"->", et qui forment la BdC. C'est regrettable, car cela entretient une
confusion avec les règles de dérivation, mais c'est l'usage.
Une règle a une
partie gauche (LHS) et une partie droite (RHS).
La LHS est une conjonction de
prémisses, c'est-à-dire que les prémisses sont reliées par des ^. La partie
droite est une conjonction de conséquents.
En Prolog, la partie droite est à
gauche, et il n'y a qu'un conséquent.
Reprenons notre S.F., avec une nouvelle
base de faits : F1 : distance.=.500km
F2 : avoir.le.téléphone
Il ne se passe rien. Le système ne sait pas, à partir du symbole
distance.=.500km , affirmer
(non distance.<.300km) . Pour
que cela soit possible, il faudrait "casser l'atome" :
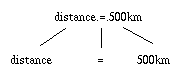
Terminologie :
- distance est un "truc valuable" (ce n'est pas une variable)
- = est un prédicat (une fonction qui renvoie "vrai" ou "faux")
- 500km est une constante
Nous avons quitté le Calcul des
Propositions, ou Logique d'ordre 0, pour une Logique que nous appellerons "0+",
dans laquelle apparaissent des "trucs valuables", des constantes, et des
prédicats. Le prix à payer est de programmer la sémantique des prédicats,
c'est-à-dire d'écrire un programme capable, par exemple, de remplacer "distance
= 500km" par "non distance < 300km". D'où la verrue sur le nez de
Mickey.
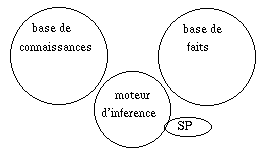
Supposons que le système me "dise"
d'aller à l'agence. Ce serait bien qu'il me dise aussi comment aller à l'agence,
sachant que la distance est de 1,5km. Mais il ne peut pas, parce que "distance"
n'est pas une variable : si j'écrase "distance = 500km" par "distance = 1,5km",
je vais obtenir des résultats contradictoires.
Solution : dupliquer le
système :
| axiomes |
R1 : distance.destination < 2km -> aller.à.pied.destination
R1a : distance.agence < 2km -> aller.à.pied.agence
R2 : ((non distance.destination < 2km)
^ distance.destination < 300km) ->
prendre.le.train.destination
R2a : ((non distance.agence < 2km)
^ distance.agence < 300km) -> prendre.le.train.agence
...
F1 : distance.destination = 500km
F2 : distance.agence = 1,5km
F3 : non avoir.le.téléphone
|
Mais supposons maintenant que je veuille
travailler sur n objets : je ne peux pas "n-pliquer" mon système. Il faut
que je puisse écrire :
R1 : quelle que soit la destination,
distance(destination) < 2km ->
aller.à.pied(destination)
destination devient alors une
variable, et j'ai introduit d'autre part "quelle que soit", qu'on
appelle le quantificateur universel, noté  .
.
Je suis à présent en Calcul des Prédicats
du Premier Ordre, ou "Logique d'Ordre 1". Mon moteur d'inférence va se
compliquer, puisqu'il va devoir chercher, non plus à faire coller un "F" avec la
partie gauche d'un "R", mais chercher quelles valeurs des variables permettent
cet appariement.
Pour définir qu'une relation R est
transitive, il suffit d'écrire :
 R (
R ( x
x  y
y  z (xRy) ^ (yRz) -> (xRz)) -> transitive
(R))
z (xRy) ^ (yRz) -> (xRz)) -> transitive
(R))
Mais on n'a pas le droit! En effet, on fait porter le quantificateur
universel sur "R", une variable de relation, alors qu'on n'a le droit de le
faire porter que sur une variable d'individu.
On passe alors à la Logique
d'Ordre 2... mais ceci est une autre histoire.
Supposons à présent que
j'écrive :
fenêtre.ouverte ^ courant.d'air ->
fermer.la.fenêtre
"fermer.la.fenêtre" est un théorème, qui doit s'entendre :
"il faut fermer la fenêtre". Mais ce qui m'interesserait, c'est qu'un robot
domotique dispose de telles connaissances, et qu'il aille effectivement fermer
la fenêtre avec ses petites mains. "fermer.la.fenêtre" devient alors une
action. Mais si mon robot ferme la fenêtre, il y aura
contradiction entre l'état du monde et sa Base de Faits, qui contiendra encore
"fenêtre.ouverte". Donc, il faut compléter :
fenêtre.ouverte ^ courant.d'air
-> fermer.la.fenêtre ^ non fenêtre.ouverte
Ce qui revient à écrire : A ^
... -> non A ^ ...
Or toute la Logique repose sur l'interdiction d'une
telle formule !
Nous créons donc (dans les années 70), les Logiques non
monotones, dans lesquelles cela n'est plus interdit. (non monotone, par analogie
avec l'Analyse : le nombre de théorèmes n'est plus une fonction non-décroissante
du temps).
 Nous gagnons en puissance
d'expression, mais nous perdons quelque chose de très important : la certitude
de terminer en temps fini. En effet, la même situation peut se reproduire
(quelqu'un ré-ouvre la fenêtre), et il faudra appliquer à nouveau la même règle
aux mêmes faits ; nous ne pouvons donc plus marquer comme au 2.2.2., et donc le
système peut boucler.
Nous gagnons en puissance
d'expression, mais nous perdons quelque chose de très important : la certitude
de terminer en temps fini. En effet, la même situation peut se reproduire
(quelqu'un ré-ouvre la fenêtre), et il faudra appliquer à nouveau la même règle
aux mêmes faits ; nous ne pouvons donc plus marquer comme au 2.2.2., et donc le
système peut boucler.
On remarquera que cette notion de
monotonie/non-monotonie est indépendante de l'Ordre de la Logique considérée
:
 Si je dis à présent à
mon robot :
Si je dis à présent à
mon robot :
oeuf.cru ^ eau.froide -> allumer.le.gaz
Dans 3 minutes, je
pourrai affirmer "non oeuf.cru". Mais pendant ces trois minutes? Donc je vais
programmer mon système pour qu'il ne fasse aucune déduction à ce propos pendant
3mn. On entre dans les Logiques temporelles.
Si je dis maintenant :
non
en.stock(article) ^ besoin(article) -> commander(article)
c'est pareil,
sauf que je ne sais pas quand arrivera le livreur.
 Jusqu'à présent, nous appuyant
sur les S.F., dans lesquels une expression est, ou n'est pas, un théorème, nous
ne nous sommes intéressés qu'au "vrai" et au "faux". Or, dans la vraie vie, les
choses ne sont pas si simples. Il y a des choses dont nous ne savons pas si
elles sont vraies ou fausses. On peut donc souhaiter manipuler les 3 valeurs :
(V ? F).
Jusqu'à présent, nous appuyant
sur les S.F., dans lesquels une expression est, ou n'est pas, un théorème, nous
ne nous sommes intéressés qu'au "vrai" et au "faux". Or, dans la vraie vie, les
choses ne sont pas si simples. Il y a des choses dont nous ne savons pas si
elles sont vraies ou fausses. On peut donc souhaiter manipuler les 3 valeurs :
(V ? F).
Mais cela peut encore sembler trop étroit : on peut avoir besoin
d'une graduation plus fine : (Vrai Probable Inconnu Improbable Faux). Et puis
pourquoi ne pas continuer? On peut considérer l'intervalle continu [-1 +1]. Mais
c'est encore simpliste : à une notion donnée, on peut associer une
certitude, comprise entre -1 et +1, et une
précision, comprise entre 0 et 1. On entre alors dans le domaine
des Logiques floues (fuzzy).
Le
problème devient alors :
Si A -> B avec une certitude CR et une
précision PR,
et si A est connu avec CA et
PA,
on peut en déduire B, mais combien valent CB et
PB?
Jusqu'ici, nous sommes restés "objectifs".
Si à présent nous voulons introduire "l'homme dans la boucle", nous pouvons
envisager des opérateurs tels que "X croit que Y est vrai", "X sait que Y est
vrai", etc. Avec des règles plus ou moins contraignantes. Par exemple, "nul
n'est censé ignorer la loi" s'écrira :  X
X
 A, A -> sait(X A).
A, A -> sait(X A).
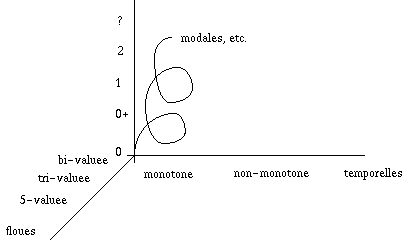 Il n'y a pas une Logique, mais un grand nombre
de Logiques. Lorsque vous décidez de résoudre un problème en faisant appel à des
connaissances, la première chose à faire est de vous situer dans l'espace à 4
dimensions ci-dessus,... et de regarder si le moteur d'inférence correspondant
existe.
Il n'y a pas une Logique, mais un grand nombre
de Logiques. Lorsque vous décidez de résoudre un problème en faisant appel à des
connaissances, la première chose à faire est de vous situer dans l'espace à 4
dimensions ci-dessus,... et de regarder si le moteur d'inférence correspondant
existe.
Dans chaque matière, le TD ne peut
pas avoir lieu avant le cours. La salle C3 contient au maximum 36 étudiants. Le
cours d'Infographie nécessite du matériel audiovisuel, qui ne se trouve que dans
les salles C1 et C2. L'effectif du cours de Probas-Stats est 70. Le cours de
Logique est commun aux deux options. Le cours de Systèmes d'Exploitation a comme
pré-requis la première moitié du cours d'Algo. Mr B. enseigne l'Algo et la
Compil. Madame S. n'est pas là le Mercredi. Monsieur C. vient de loin, il faut
lui grouper ses cours sur une journée. Si on met Probas-Stats et Méthodes
Numériques le même jour, les étudiants déjantent. Si ils n'ont pas cours de 10h
à 16h, ils risquent de ne pas revenir à 16h... Faites moi l'emploi du
temps.
Je viens d'apprendre que Mr A. a eu un accident ; il est en arrêt pour
trois semaines. Aménagez-moi l'emploi du temps.
Dans un tel problème, on distingue :
- des contraintes fortes : la même personne ne peut faire deux cours
simultanément
- des contraintes faibles : il vaut mieux ne pas placer un cours le Vendredi
de 16h à 18h
- une fonction à optimiser : de deux solutions, on choisira celle qui fait
faire le moins d'aller-retours aux enseignants qui effectuent leur recherche
ailleurs que sur le campus
Dans de tels problèmes, on distingue
également :
- les problèmes sur-contraints : n'importe comment, il faudra violer
certaines des contraintes faibles, car il n'y a pas de solution
- les problèmes sous-contraints : on a l'embarras du choix, donc on va
s'attacher à minimiser la fonction coût
- les problèmes qui ont une solution et une seule : montrez m'en un!
On distingue d'autre part :
- les problèmes booléens : chaque variable vaut soit "vrai" soit "faux".
Exemple : l'Anglais habite la maison rouge, l'Allemand boit de la bière, le
Français a un chien, la maison bleue n'est pas à côté de la maison de
l'Italien... qui boit du jus de citron?
- les problèmes en nombres entiers. Exemple : mon sac à dos contient au plus
45kg, une boite de choucroute pèse 1kg et m'apporte 100cal, 15 lipides, 12
glucides, une tablette de chocolat pèse 100g et m'apporte 250cal,... comment
dois-je remplir mon sac pour avoir le maximum d'énergie avec un régime
équilibré?
- les problèmes en nombres "réels". Exemple : calculer la puissance
nécessaire pour le ventilateur, sachant que plus il est gros plus il évacue de
chaleur, mais que plus il est gros plus son moteur chauffe.
- les problèmes non numériques. Exemple : quelle forme donner à la voiture
pour qu'elle séduise un maximum de clients? Nous n'aborderons pas ici ces
problèmes.
Enfin, on peut considérer différents types de contraintes :
- les contraintes unaires : x < 5
- les contraintes binaires : le fil A ne doit pas toucher le fil B
- les contraintes ternaires : aucun obstacle ne doit se trouver sur la
droite reliant la lampe à la cellule photo-élecctrique
- etc : la distance entre A et B doit être inférieure à la distance entre C
et D
Par ailleurs, en ce qui concerne la solution, tout dépend si :
- je veux la solution optimale
- je me contenterai d'une solution approximative dans x minutes
- il me faudra une solution, mais je ne sais pas quand ("anytime
algorithms")
Un problème de satisfaction de
contraintes (CSP) est un quadruplet [X, D, C, f], où
- les Xi sont les variables,
- les Di sont les domaines possibles pour chaque variable,
- les Cj sont les contraintes, et
- f est une fonction à minimiser.
Dans certains cas, f
n'existe pas, on serait déjà bien content de trouver une solution. Nous
n'aborderons pas ici les problèmes d'optimisation multi-critères, dans lesquels
il y a plusieurs fonctions à minimiser.
On appelle affectation,
le fait d'instancier certaines variables Xi par des valeurs
xi (évidemment prises dans les domaines Di). Cette
affectation peut être totale (elle concerne toutes les variables
du problème) ou partielle. Une affectation est
consistante si elle ne viole aucune des contraintes dans
lesquelles interviennent ses variables.
Exemple : 4 personnes, U D C X,
doivent traverser un pont. Le pont ne supporte que deux personnes. Il faut une
lampe pour traverser, et on n'a qu'une lampe. U met 1 minute, D 2, C 5, et X 10.
Si deux personnes traversent ensemble, c'est à la vitesse de la plus
lente.
Il est clair qu'on va faire traverser 2 personnes, en faire revenir 1,
traverser 2, revenir 1, et enfin traverser 2.
On a donc 8 variables : V11,
V12, V2, V31, V32, V4, V51 et V52.
Le domaine est (U D C X)
Aux
contraintes du texte s'ajoute l'évidence : Vij différent de Vik
Je peux
affecter : UDCX /
X à V11 et U à V12 (coût : 10) DC / UX
U à V2 (11) DCU / X
D à V31 et C à V 32 (16) U / DCX
C à V4 (21) UC / DX
C à V51 et U à V52 (26) / UDCX
J'ai une affectation totale, consistante.
Ajoutons une contrainte : le
temps total doit être inférieur à 21. UDCX /
X à V11 et U à V12 (coût : 10) DC / UX
U à V2 (11) DCU / X
D à V31 et C à V 32 (16) U / DCX
C à V4 (21) UC / DX
Cette affectation partielle n'est pas consistante. Je vais donc
backtracker. Au lieu de faire revenir C, je fais revenir X : UDCX /
X à V11 et U à V12 (coût : 10) DC / UX
U à V2 (11) DCU / X
D à V31 et C à V 32 (16) U / DCX
X à V4 (26) UX / DC
Inconsistance, je backtracke. UDCX /
X à V11 et U à V12 (coût : 10) DC / UX
U à V2 (11) DCU / X
D à V31 et C à V 32 (16) U / DCX
D à V4 (18) UD / CX
Et je repars UD / CX
U à V51 et D à V52 (20) / UDCX
Gagné. Mais cette affectation est-elle optimale?
Pour le savoir,
relançons le backtrack
- bien que nous ayons une solution
- évidemment en nous arrêtant dès que nous trouvons une solution pire qu'une
solution que nous avons déjà
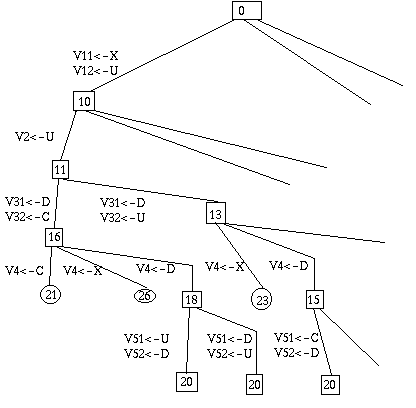
Au bout d'un temps... largement supérieur à
20 minutes, nous allons trouver une solution meilleure, en 17 minutes. Au bout
d'un temps encore plus grand, nous aurons épuisé tous les cas, ce qui nous
permettra de prouver que la solution optimale coûte 17 minutes.
Si, au lieu
de faire développer cet arbre par une machine, nous utilisons notre
intelligence, nous parvenons au raisonnement suivant :
- C'est X qui coûte le plus cher, c'est à lui que je dois m'intéresser en
premier (ce qui ne signifie pas que c'est lui que je doive faire passer en
premier)
- Il faut qu'il passe, ce qui me coûte 10, il ne faut pas qu'il revienne, ce
qui me coûterait 30
- Ensuite, c'est C qui coûte le plus cher, mais s'il passe avec X il ne me
coûte rien!
- Il faut donc qu'ils passent ensemble, et qu'ils ne reviennent pas.
- Donc ils ne peuvent pas faire partie du premier voyage (l'un des deux doit
rapporter la lampe)
- Et pas non plus du dernier (l'un des deux doit avoir rapporté la lampe).
- Donc le premier voyage concerne U et D, et le dernier aussi.
Ce
raisonnement est séduisant (merci), mais est-il généralisable à plusieurs
milliers de variables? Non bien sûr. Toutefois, il fait apparaître deux choses :
- Il semble utile de s'intéresser d'abord aux éléments les plus contraints
- Il n'est peut-être pas nécessaire d'envisager tous les cas.
Le
premier point ci-dessus illustre la notion de (méta)-heuristique
(cf big
rocks).
Le second point introduit la notion de méthode
incomplète.
Une méthode incomplète ne cherche pas à envisager tous
les cas, mais cherche à trouver le plus vite possible une solution acceptable :
arrivé à un noeud de l'arbre,
- on élimine (définitivement ?) certaines branches
- on ordonne les branches à explorer
Il est donc possible qu'on ne
trouve pas la solution optimale ; il est par ailleurs certain que l'on ne pourra
pas prouver que la solution trouvée est optimale. Il est même admissible que la
solution trouvée viole certaines contraintes.
Ces méthodes nécessitent
l'introduction de notions plus fines que la simple consistance :
Un problème
est dit k-consistant si, quelle que soit une affectation
consistante de k-1 variables, et quelle que soit une autre variable
Xk, on peut trouver une affectation consistante pour
Xk.
Un problème est dit noeud-consistant s'il est
1-consistant, c'est-à-dire si on peut affecter n'importe quelle valeur (dans le
domaine, bien sur) à n'importe quelle variable sans violer aucune contrainte. En
d'autres termes, le problème est bien posé.
Ces définitions n'ont pas grand
intérêt a priori. Elles en prennent lorsqu'on progresse, c'est-à-dire lorsqu'on
a déjà proposé une affectation partielle et qu'on considère le sous-problème
restant.
Certaines méthodes incomplètes consistent à donner une première
affectation totale, probablement non consistante, puis à la perturber
astucieusement pour l'améliorer. Supposez par exemple que vous vouliez faire
entrer un maximum de petits pois dans une boîte : vous en mettez autant que vous
pouvez, puis vous secouez la boîte, et vous pouvez alors en rajouter (attention,
cette méthode est inefficace à bord d'un vaisseau spatial).
Nous verrons au
chapitre 8
d'autres méthodes de ce style.
 Chapitre précédent
Chapitre précédent  Chapitre suivant
Chapitre suivant  Table des matières
Table des matières
Attention, ce fichier n'est peut-être plus d'actualité s'il est dans votre cache
; vérifiez la date du copyright, et faites éventuellement un 'reload'.
©
Jean-Marc Fouet, 31-10-1999 
 Réponses
:
Réponses
:

 Donc les notions de "être un
théorème" et de "être un non-théorème" ne sont pas symétriques.
Notre système "peu" est semi-décidable : nous avons une procédure qui répond
"oui" en temps fini, mais pas de procédure pour répondre "non".
Donc les notions de "être un
théorème" et de "être un non-théorème" ne sont pas symétriques.
Notre système "peu" est semi-décidable : nous avons une procédure qui répond
"oui" en temps fini, mais pas de procédure pour répondre "non".
 Si nous remplaçons "plus " par "+", "egal " par
"=", et "un " par "1", l'axiome s'écrit : 1+1=2 , en base 1 (les chiffres
romains, concaténation = addition).
Si nous remplaçons "plus " par "+", "egal " par
"=", et "un " par "1", l'axiome s'écrit : 1+1=2 , en base 1 (les chiffres
romains, concaténation = addition). Une
interprétation d'un S.F. n'est en général pas équivalente au S.F.,
c'est-à-dire que les notions de "être un théorème" et "être un non-théorème"
d'une part, et de "être vrai" et "être faux" d'autre part, peuvent ne pas se
recouvrir.
Une
interprétation d'un S.F. n'est en général pas équivalente au S.F.,
c'est-à-dire que les notions de "être un théorème" et "être un non-théorème"
d'une part, et de "être vrai" et "être faux" d'autre part, peuvent ne pas se
recouvrir.



 NON! C'est vrai dans
l'interprétation, mais ce n'est pas un théorème du système formel ! Nous n'avons
pas écrit, et encore moins programmé :
NON! C'est vrai dans
l'interprétation, mais ce n'est pas un théorème du système formel ! Nous n'avons
pas écrit, et encore moins programmé :
 NON! C'est vrai en Logique,
mais pas en Informatique ! Notre programme va continuer à produire :
NON! C'est vrai en Logique,
mais pas en Informatique ! Notre programme va continuer à produire : 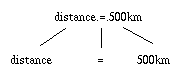

 .
. R (
R ( x
x  y
y  z (xRy) ^ (yRz) -> (xRz)) -> transitive
(R))
z (xRy) ^ (yRz) -> (xRz)) -> transitive
(R))  Nous gagnons en puissance
d'expression, mais nous perdons quelque chose de très important : la certitude
de terminer en temps fini. En effet, la même situation peut se reproduire
(quelqu'un ré-ouvre la fenêtre), et il faudra appliquer à nouveau la même règle
aux mêmes faits ; nous ne pouvons donc plus marquer comme au 2.2.2., et donc le
système peut boucler.
Nous gagnons en puissance
d'expression, mais nous perdons quelque chose de très important : la certitude
de terminer en temps fini. En effet, la même situation peut se reproduire
(quelqu'un ré-ouvre la fenêtre), et il faudra appliquer à nouveau la même règle
aux mêmes faits ; nous ne pouvons donc plus marquer comme au 2.2.2., et donc le
système peut boucler.


 X
X
 A, A -> sait(X A).
A, A -> sait(X A).

 Chapitre précédent
Chapitre précédent  Chapitre suivant
Chapitre suivant  Table des matières
Table des matières