3. Notion de méta-système

Au 2.1.3. , nous avons déploré de devoir "tricher" pour démontrer qu'une expression du S.F. "peu" était un non-théorème. Nous allons à présent formaliser cette tricherie.

3.1. Définition

Nous sommes sortis du S.F. "peu" pour aller faire de l'arithmétique. Or l'arithmétique constitue elle-même un S.F., le S.F "AF" (Arithmétique Formelle), décrit par les axiomes de Peano.

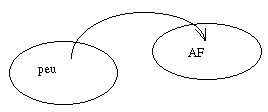
Nous dirons que "AF", qui est le SF dans lequel nous allons pour résoudre les problèmes insolubles dans "peu", est le méta-système de "peu".

3.2. Un méta-théorème

Au 2.1.5., nous avons vu que l'interprétation, bien que non équivalente au S.F., pouvait guider une démonstration. Si par exemple je demande si "uuuuuuuupuuueuuuuuuuuu" est un théorème, vous allez traduire par "8+3=9", et vous dire que c'est probablement un non-théorème, donc qu'il faut chercher une astuce, par exemple en faisant de l'arithmétique. Si par contre je propose : "uuuuupuuuuueuuuuuuuuuu", vous traduisez "5+5=10", et vous vous dites que ça vaut la peine de développer l'arbre jusqu'à profondeur 11.
Formalisons cela, en nous plaçant dans le méta-système AF, et en démontrant le méta-théorème suivant :
une expression est un théorème de "peu" si et seulement si elle est de la forme : ux p uy e ux+y
Dorénavant donc, si on me propose une expression, J'ai donc une procédure qui répond à tout coup : mon système, qui était semi-décidable, est maintenant décidable. De plus, cette procédure est en O(n), au lieu du O(2n/2) du développement de l'arbre. J'ai donc gagné qualitativement et quantitativement!

3.3. Théorèmes de Gödel

Au début du XXème siècle, Hilbert, dans son célèbre "programme", a posé, entre autres, une question que nous pourrions reformuler ainsi : puisque le passage de "peu" à son méta-système "AF" est si fructueux, dans quel système peut-on passer quand on a un problème insoluble dans "AF"?
Kurt Gödel a répondu en 1930 : le méta-système de AF, c'est... AF.

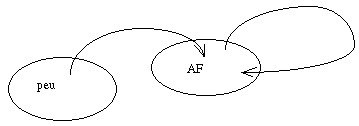
Pour démontrer que AF est son propre méta-système, il associe à chaque symbole un code numérique, et fait ensuite des opérations sur les codes des expressions, nous n'entrerons pas dans les détails. Mais, à peine un an plus tard, ayant poursuivi ses travaux sur cette question, il fait exploser une énorme bombe : puisque AF est son propre méta-système, il existe des expressions dont on ne peut rien dire (théorème ou non-théorème) ou dont on peut dire n'importe quoi ! Nous n'entrerons pas dans les détails, mais donnerons simplement deux pseudo-exemples.
Considérons l'ensemble des entiers positifs que l'on peut écrire en français avec moins de 200 caractères ASCII. Appelons-le E. Cet ensemble n'est pas vide. Exemples :
10 , dix , 10 puissance 10 , le nombre de protons de l'univers , etc.
Mais il est fini. Donc il admet un complémentaire dans N, appelons-le C. Considérons le complémentaire dans N de l'ensemble des entiers positifs que l'on peut écrire en français avec moins de 200 caractères ASCII. Ce complémentaire est infini, donc non vide, donc admet un plus petit élément. Considérons le plus petit élément du complémentaire dans N de l'ensemble des entiers positifs que l'on peut écrire en français avec moins de 200 caractères ASCII.
Il est dans C, puisqu'il en est le plus petit élément. Mais il est dans E, puisque ma phrase ne fait pas 200 caractères !
Ne cherchez pas l'astuce : en comptant les caractères d'une formule arithmétique, je me suis exposé à ce qu'avait démontré Gödel. Une autre?
Cette phrase contient quatre fois la consonne "c". Alors :
Celle-ci contient cinq fois la consonne "c". Euh, pardon :
Celle-ci contient six fois la consonne "c". !!!

Cette découverte est très grave, car elle met fin à 2400 ans de travaux conduits dans l'espoir de formaliser le raisonnement et le discours. Elle est très fructueuse car elle relance la recherche sur d'autres terrains (voir théorie des Topoï).
Chapitre précédent Chapitre suivant Table des matières
Attention, ce fichier n'est peut-être plus d'actualité s'il est dans votre cache; vérifiez la date du copyright, et faites éventuellement un 'reload'
© Jean-Marc Fouet, 25-10-1999