6. Découverte de connaissances
Au 1.2., nous
avons vu comment, à l'aide d'heuristiques (connaissances), on pouvait résoudre
en temps quasi-linéaire un problème dont on avait, par ailleurs, démontré qu'il
était de complexité exponentielle.
 Je
vous ai menti! Le problème que nous avons résolu est "SEND+MORE=MONEY". Le
problème de complexité exponentielle est celui de la cryptarithmétique.
Je
vous ai menti! Le problème que nous avons résolu est "SEND+MORE=MONEY". Le
problème de complexité exponentielle est celui de la cryptarithmétique.
De
même le joueur d'échecs résout-il le problème qu'on lui pose, et non pas
le problème de jouer un coup quelle que soit la situation.
On peut
définir un ensemble :
- en intension, en donnant les propriétés communes à tous ses éléments, ou
- en extension, en énumérant ses éléments
Oui, direz-vous, mais s'il
y a un nombre infini d'éléments? Citez-moi, vous répondrai-je, un ensemble ayant
un nombre infini d'éléments.
Il n'en reste pas moins que notre objectif, dans
ce chapitre "découverte de connaissances", est de passer de l'extensionnel à
l'intentionnel. Simplement, nous aurons la modestie de ne pas dire "tous les x
qui vérifient P vérifient Q ", mais "beaucoup d'x qui...". En d'autres termes,
nous cherchons à élaborer des règles, en admettant qu'elles souffrent des
exceptions... ce qui est le cas de toutes les règles :-)
Considérons le raisonnement
suivant : Jean Blanc a volé mon portefeuille.
Jean Noir a volé le vélo de mon fils.
Donc tous les "Jean" sont des voleurs.
Vous m'accorderez que cette inférence est abusive. En fait, il aurait
fallu dire : tous les "Jean" de couleur sont des voleurs
:-)
L'induction consiste à passer d'une définition
extensionnelle d'un ensemble à sa définition intensionnelle. Ce n'est pas une
inférence valide, dans la mesure où on ne peut pas prouver qu'à
partir de faits vrais elle produit une règle vraie. Et pourtant, elle est bien
utile.
Considérons à présent le raisonnement suivant : Tous les hommes sont mortels.
Socrate est mortel.
Donc Socrate est un homme.
Vous m'accorderez que cette inférence est abusive. En fait, Socrate est le
nom d'un pois rouge (comme tous les pois), qui vient de
décéder.
L'abduction consiste à considérer que, si on observe
l'effet, on peut supposer la présence de la cause. Ce n'est pas non plus une
inférence valide, mais elle aussi est bien utile.
Le problème, dans
l'inférence par induction, est de déterminer quels sont les attributs
pertinents, discriminants (or on ne peut connaitre tous les attributs, cf. 5.4.3.).
Un exemple frappant est celui du tableau de Mendeleiev : avant, on devait
apprendre tout ce qu'on pouvait sur chaque corps pur. Il a l'idée de les
ordonner suivant leur masse atomique (alors que dans la nature, on les trouve
sous forme de molécules). Il remarque alors une "certaine" régularité des
valences électriques. Et l'idée jaillit, de les organiser dans un tableau à deux
dimensions. 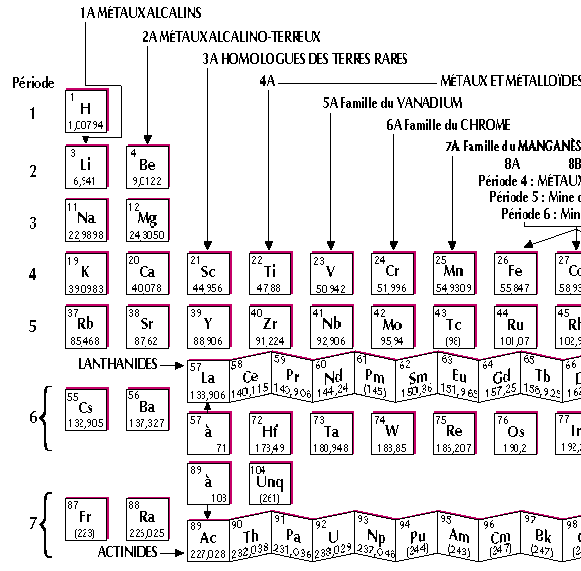
Et dorénavant, on a
beaucoup moins de choses à apprendre : il suffit de regarder dans quelle colonne
est le corps.
Mieux encore (abduction) : Mendeleiev a pu immédiatement
soupçonner certaines mesures d'être fausses, parce que le corps n'était pas dans
la bonne ligne.
Et enfin, le triomphe : il a pu, par déduction, décrire des
corps qui n'avaient jamais encore été observés, pour remplir les cases vides de
son tableau. Il fallut des dizaines années pour les découvrir dans la nature à
l'état de traces.
Un autre moyen de découvrir des connaissances
consiste à remarquer que le domaine sur lequel on travaille "ressemble" à un
autre, et que donc, peut-être, ce qui est connu dans le deuxième peut servir
dans le premier.
Exemple :
Considérons un carré 8*8, et des
rectangles 1*2 :
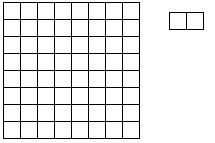
Il est évident que
l'on peut recouvrir le carré avec 32 rectangles. Considérons à présent un
nouveau problème de recouvrement :
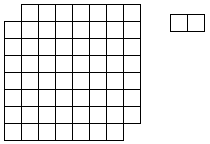
Peut-on encore couvrir, avec 31 rectangles?
L'algorithme consiste à essayer tous les cas, il est terriblement combinatoire.
Mais cette figure nous fait penser à un échiquier et des dominos

Ce qui nous fait penser aux couleurs : les
dominos apportent 31 blancs et 31 noirs, alors que l'échiquier tronqué contient
30 blancs et 32 noirs. Donc : non.
Autre exemple :
Considérons
l'addition dans N. Elle est commutative. Elle a un élément neutre (0).
Etant donné un nombre quelconque supérieur à 2, on peut trouver plein de couples
dont la somme soit ce nombre :  z,
z,  x#0,
x#0, 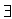 y#0, x+y =z
y#0, x+y =z
Considérons la multiplication. Elle est commutative. Elle a un
élément neutre (1). A-t-on la propriété  z,
z,
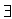 x#1,
x#1, 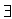 y#1, x*y =z ? Pas toujours. Et on introduit la
notion de nombre premier.
Ma tondeuse autoportée
refuse de démarrer. Plus exactement, je peux la démarrer en tirant sur la
ficelle, mais le démarreur, lui, ne fonctionne pas. Pourtant, si je le branche
directement sur la batterie, il fonctionne. L'an dernier, c'était la machine à
laver qui ne fonctionnait pas, alors que le moteur tournait si je le branchais
directement sur le secteur. Le réparateur m'a expliqué qu'il y a une sécurité
qui empèche de fonctionner si la porte n'est pas fermée, et que c'est cette
sécurité qui était grippée (un petit ressort qui s'était détendu). Sur ma
tondeuse aussi, il y a une sécurité, qui empèche de démarrer si le frein à main
n'est pas mis. Je shunte cette sécurité, et ça démarre.
y#1, x*y =z ? Pas toujours. Et on introduit la
notion de nombre premier.
Ma tondeuse autoportée
refuse de démarrer. Plus exactement, je peux la démarrer en tirant sur la
ficelle, mais le démarreur, lui, ne fonctionne pas. Pourtant, si je le branche
directement sur la batterie, il fonctionne. L'an dernier, c'était la machine à
laver qui ne fonctionnait pas, alors que le moteur tournait si je le branchais
directement sur le secteur. Le réparateur m'a expliqué qu'il y a une sécurité
qui empèche de fonctionner si la porte n'est pas fermée, et que c'est cette
sécurité qui était grippée (un petit ressort qui s'était détendu). Sur ma
tondeuse aussi, il y a une sécurité, qui empèche de démarrer si le frein à main
n'est pas mis. Je shunte cette sécurité, et ça démarre.
Qu'ai-je fait?
- J'ai cherché en mémoire un cas de problème similaire
- J'ai adapté la solution à mon problème d'aujourd'hui
- Puis j'ai mémorisé ce nouveau cas, pour utilisation ultérieure
La
première étape est probablement la plus difficile à automatiser. Elle relève
typiquement de l'analogie évoquée au paragraphe précédent. Elle impose de savoir
calculer une distance entre le problème actuel et les problèmes en
mémoire. Comme pour le raisonnement par induction, cela suppose que l'on sache
discerner les paramètres pertinents (problème avec un moteur électrique, qui
pourtant fonctionne, présence de sécurités) des autres (machine dans la maison
contre machine en plein air, machine usagée contre machine quasi-neuve, machine
utilisé toute l'année contre machine utilisée quand il fait beau...).
Elle
suppose également une représentation hiérarchique (démarreur = sorte de moteur
électrique, etc.) ainsi que nous allons en voir au paragraphe suivant.
Elle
suppose, enfin, que l'on aît correctement énoncé le problème, éventuellement
lors d'un dialogue.
La deuxième étape impose de posséder des opérateurs
de transformation de la solution (la sécurité de la machine à laver est dans la
porte, celle de la tondeuse sous la pédale de frein).
On peut également,
plutot que de transposer la solution (passif), transposer la
résolution (actif).
Enfin, il peut y avoir une étape "2bis", de
réparation de la solution, si celle-ci n'est pas applicable.
La troisième
étape peut ne pas consister simplement à stocker le nouveau cas à côté du
précédent (mémoire plate), mais à les fusionner en un cas plus abstrait (mémoire
hiérarchique) : MOPS, construction bottom-up des scripts.
On peut y stocker
des index positifs (faits pertinents), mais aussi négatifs (faits
différentiels).
Remarque : la méthode s'applique à des problèmes statiques
(frames de Minsky), et à des problèmes dynamiques (scripts de
Schank).
Exemple : Cyrus
Lorsqu'on aborde un domaine
nouveau, on bute sur le vocabulaire : d'une part sur les mots qu'on ne connait
pas, d'autre part sur les mots qu'on connait mais qui n'ont pas ici le même
sens. Dans le premier cas, on va regarder dans le dictionnaire ; dans le
deuxième cas, dès qu'on a pris conscience qu'il y avait un problème, on va
regarder dans le glossaire. Mais, dans les deux cas, on va trouver, dans la
définition, des mots sur lesquels on butera : le dictionnaire est
circulaire!
En fait, ce nouveau domaine ne consiste pas simplement en "mots"
; il comporte une "structure", et c'est cela que nous cherchons à
"comprendre".
On appelle "ontologie" d'un domaine l'ensemble des mots et
structures qui le constituent. Ainsi que nous l'avons vu au 5.4.2., les
langues ne sont pas très appropriées pour transmettre les ontologies. Et si la
cible est une machine, elles sont hors de question, pour de longues années
encore. On préfère donc avoir recours à des langages, comme par exemple les
langages "orientés objet". En représentation externe, on privilégiera une
représentation sous forme de graphes, plus lisible que la représentation interne
sous forme de listes (attributs - valeurs).
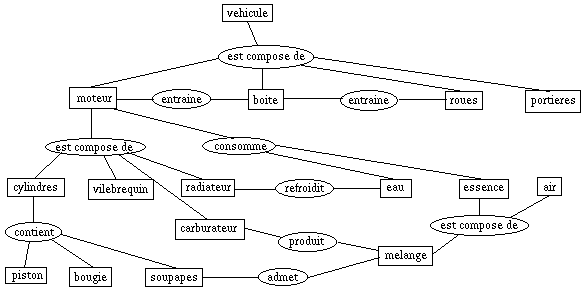
On peut distinguer deux méthodes pour
construire une ontologie : top-down et bottom-up. Dans tous les cas, dans l'état
actuel, il faut procéder incrémentalement, c'est-à-dire par améliorations
successives. Une partie des recherches est axée sur la construction à partir de
textes, et pose donc les problèmes de compréhension automatique de textes et de
schémas.
Le graphe ci-dessus laisse entrevoir la complexité de la tâche. Un
outil extrèmement utile consiste à extraire des sous-graphes, si possible des
arbres, en ne visualisant que certaines relations. Cela permet, souvent de
"faire sauter aux yeux" des relations manquantes (regardez l'air, ci-dessus) ou
des relations surprenantes.
Une autre question qui se pose est celle du
"point de vue" : pour un véhicule, par exemple, le carrossier, le motoriste,
l'acousticien... sont tous intéressés par le moteur, mais à des titres très
divers. Sans parler du fabricant, du vendeur et du réparateur.
 Chapitre précédent
Chapitre précédent  Chapitre suivant
Chapitre suivant  Table des matières
Table des matières
Attention, ce fichier n'est peut-être plus d'actualité s'il est dans votre cache
; vérifiez la date du copyright, et faites éventuellement un 'reload'.
©
Jean-Marc Fouet, 1-11-1999  Je
vous ai menti! Le problème que nous avons résolu est "SEND+MORE=MONEY". Le
problème de complexité exponentielle est celui de la cryptarithmétique.
Je
vous ai menti! Le problème que nous avons résolu est "SEND+MORE=MONEY". Le
problème de complexité exponentielle est celui de la cryptarithmétique.



 z,
z, 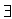 x#0,
x#0, 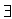 y#0, x+y =z
y#0, x+y =z z,
z,
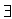 x#1,
x#1, 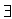 y#1, x*y =z ? Pas toujours. Et on introduit la
notion de nombre premier.
y#1, x*y =z ? Pas toujours. Et on introduit la
notion de nombre premier.

 Chapitre précédent
Chapitre précédent  Chapitre suivant
Chapitre suivant  Table des matières
Table des matières