7. Validation de connaissances

7.1. Problématique

Nous avons déjà eu l'occasion d'insister sur la notion de contexte (5.4.4.) et de "non dit" (5.4.3.). Par exemple, si l'on considère le dimensionnement de roulements à billes, celui qui travaille pour l'automobile a des règles complètement différentes de celui qui travaille pour le spatial, parce que pour le premier il est évident que les roulements baignent dans l'huile, alors que pour le second il est évident qu'ils frottent "à sec". Et même dans le spatial, celui qui s'occupe de la turbo-pompe qui tourne à 40.000 t/mn pendant 8 minutes n'a pas du tout les mêmes règles que celui qui s'occupe d'un satellite qui tourne à 1 t/h pendant 15 ans.
On obtiendra donc des règles parfaitement contradictoires, qui ne seront utilisables que si on précise leur contexte d'utilisation.
Autre exemple : celui qui conçoit une moto vous dira que sur le moyeu de la roue avant il faut mettre un boulon de 13. Or le calcul montre que du 10 serait largement suffisant. L'explication ne relève pas de la Mécanique : c'est simplement que, puisque sur la roue arrière on a besoin d'un boulon de 13, en mettre un aussi sur la roue avant diminue le besoin d'outillage.
On a donc besoin de détecter les contradictions dans les Bases de Connaissances. D'autre part, il serait vain de croire que l'expert pensera à énumérer tous les cas : il faut donc pouvoir détecter des lacunes. Ensuite, il est inévitable qu'il se répète, qu'il donne une règle pour un cas particulier et la même pour le cas général. Cela fera perdre du temps. Il faut donc pouvoir détecter les redondances. Enfin, une erreur peut toujours se glisser, faisant qu'une règle est inapplicable (ses conditions ne peuvent jamais être réunies). Il convient donc de savoir détecter les incompatibilités entre prémisses.

7.2. Validation dynamique

Comme pour les programmes traditionnels, il est indispensable de soumettre un SBC à des jeux d'essai. En d'autres termes, on va fabriquer des Bases de Faits, et faire tourner le système dessus, puis analyser le résultat.
Une technique semi-automatique de fabrication de jeux d'essais consiste à s'intéresser aux extrèmes : décrire une situation dans laquelle la température est la plus basse de celles mentionnées dans les règles, la pression la plus haute possible, etc.
Il est important que l'expert qui a fourni les règles soit tenu à l'écart de la constitution d'au moins une partie des jeux d'essais, car son bon sens l'empècherait d'en construire certains. En d'autres termes, on cherche avant tout à violer les règles qu'il n'a pas données.

7.3. Validation statique

La validation dynamique, bien qu'indispensable, est coûteuse. Il est intéressant, avant de s'y livrer, de vérifier statiquement la BdC, comme on relit un programme avant de le tester. Nous allons donc regarder de quelles méta-connaissances on a besoin pour vérifier une Base de Connaissances.

7.3.1. Hypothèses de travail

Nous faisons l'hypothèse que notre BdC est constituée de règles du Calcul des Prédicats du Premier Ordre (2.3.2.). Chaque prémisse et chaque conséquent est constitué d'un prédicat, éventuellement nié, portant sur des variables et/ou des constantes.

P(?x ?y) ^ non Q(a ?y) ^ R(?x ?z) ^ ...  -> S(?x) ^ T(?x ?y) ^ ...

Nous faisons d'autre part l'hypothèse que les constantes présentes dans les règles, et celles par lesquelles on va instancier les variables, sont des "objets", liés entre eux par des relations, et sur lesquels on peut faire porter des propriétés. Entre autres relations, nous supposons qu'on a un arbre d'héritage : tout objet, sauf un, "est-un" autre objet.
Nous faisons enfin l'hypothèse que les prédicats sont eux-mêmes des objets, sauf quelques prédicats numériques tels qu < , =, etc.
Dans la quasi-totalité des cas, nous traiterons des prédicats à deux places ; la première place sera appelée "sujet" et la seconde "complément".

7.3.2. Typage des variables

Dans plusieurs des méthodes qui seront exposées ci-après, nous ferons référence au "type" des variables. Cette notion est liée à la relation "est-un" mentionnée ci-dessus. Considérons la règle :

est-un(?x véhicule) ^ a-pour-bougie(?x ?y) ^ ...

Pour nous, il est évident que ?y ne peut être instancié que par quelque chose qui "est-un" "bougie". Parce que nous interprètons (2.1.5.) la règle. Mais pour le moteur d'inférence, qui travaille, faut-il le rappeler, au niveau syntaxique du Système Formel, rien de tel. Cependant, nous pouvons construire un outil qui retrouve ce résultat : il suffit qu'il aille explorer le réseau des objets, pour découvrir que tous les objets sur lesquels pointe la relation "a-pour-bougie" ont la propriété d'hériter directement de l'objet "bougies".

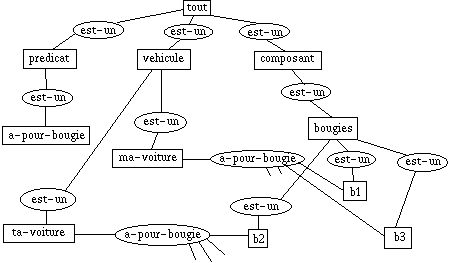
Dans ce qui suit, nous serons amenés à manipuler trois notions de type :

type "strict" : l'objet immédiatement au-dessus dans la relation "est-un"
"plus petit type commun" : l'objet le plus bas dont héritent des objets qui n'ont pas tous le même type strict. Par exemple, si b1 est une bougie et p1 un pneu, leur pptc sera "composant".
type "large" : n'importe lequel des objets au-dessus.

Muni de ces notions, on peut donc automatiquement détecter, de proche en proche, le type strict ou le pptc de chaque variable de la règle (le type strict de chaque constante étant bien entendu immédiatement connu). On s'appuie pour cela sur deux considérations :

le pptc des cibles des relations (compléments)
le pptc des origines des relations (sujets)

Ces ensembles peuvent être mis à jour au fur et à mesure qu'on utilise le système, en étudiant chaque nouvelle Base de Faits

7.3.3. Contrôles locaux

Nous considérons pour l'instant une règle isolée, sans nous préoccuper de ses éventuels conflits avec d'autres règles.

7.3.3.1. Erreur de type

L'algorithme ci-dessus peut arriver à un pptc vide.

a-pour-bougie(?x ?y) ^ est-gonflé-à-la-pression(?y ?z) ^ ...

dénote probablement une faute de frappe sur ?y. En tout cas, la règle ne sera jamais déclenchable.

7.3.3.2. Valeur impossible

Lors de la construction de l'ontologie, on peut associer à certains objets des limitations sur les valeurs possibles de certaines de leurs propriétés ; on peut de même associer directement ces limitations aux objets-propriétés. Ces limitations peuvent être faites soit en intension (intervalles obligatoires ou interdits), soit en extension (listes de valeurs permises ou interdites).
L'algorithme de typage peut alors, parallèlement, tenir à jour cette contrainte, et en détecter des violations, moyennant éventuellement la connaissance de la sémantique des prédicats numériques :

est-un(?x Ferrari) ^ a-pour-couleur(?x ?y) ^ est-un(?z pneu) ^ 
                                         a-pour-couleur (?z ?y)
est-un (?x humain) ^ a-pour-age(?x ?y) ^ >(?y 150)

7.3.3.3. Prédicats incompatibles

On peut également indiquer, lors de l'élaboration, des incompatibilités entre prédicats.

incompatibilité faible : les deux prédicats ne peuvent pas porter sur les mêmes variables.
```
a-pour-père(?x ?y) ^ a-pour-mère(?x ?y)
```
incompatibilité forte : les deux prédicats ne peuvent pas porter sur le même sujet.
```
a-pour-mari(?x ?y) ^ a-pour-femme(?x ?z)
```

7.3.3.4. Prédicats monovalués

Un prédicat est dit monovalué si, pour chaque valeur de son sujet, il y a au plus une valeur du complément. Sinon, le prédicat est dit multivalué.
Exemples : a-pour-taille est monovalué, a-pour-enfants multivalué.
Donc, si un prédicat est monovalué, on ne peut pas le trouver à gauche et à droite d'une règle avec le même sujet.

... ^ taille(?x ?y) ^ ... -> taille(?x ?z)

Remarque importante : ce contrôle n'est possible que si on est en Logique Monotone, ou si le prédicat est marqué comme étant monotone :

position(?x ?y) ^ déplacement (?x ?z) ^ +(?y ^?z ^?t) -> position(?x ?t)

Il manque des règles, ou
le prédicat est supposé affirmé dans la BdF, et il convient de le marquer comme tel

On fait de même pour les prédicats de la partie droite, ce qui permet de détecter qu'il manque des règles, ou que le prédicat est réservé à la solution.

7.3.4.3. Violation de contraintes

Une "bonne" ontologie contient des contraintes : les choses qui doivent toujours être vérifiées, et celles qui sont interdites. Par exemple, l'age d'un humain doit être inférieur à 150, une voiture ne vole pas, etc.
Pour montrer qu'une règle viole une contrainte, une technique consiste à construire une BdF virtuelle : on réifie les variables, en respectant leur type, et en leur associant les propriétés énoncées par la règle. Puis on applique à cette BdF toutes les règles possibles, en vérifiant au passage les contraintes. Lorsque ce processus de saturation s'épuise, on repart en chainage arrière, cherchant les objets qui ont pu produire ceux de la BdF. On alterne ainsi les deux processus, jusqu'à ce qu'une contrainte soit violée ou que plus aucune règle ne s'applique.
Remarquer que ce procédé se complique terriblement lorsque certaines règles sont non monotones ; on est alors obligé de gérer une pile de BdF virtuelles.

7.3.4.4. Méta-vérification

Si les contraintes sont énoncées sous la même forme que les règles, on peut les vérifier avec le même outil.

7.4. Traçabilité

Lorsque le système donne une réponse fausse, ou surprenante, nous avons vu au 2.2.3. que l'on pouvait lui demander d'expliquer son raisonnement. Il va donc nous exhiber une séquence de règles. Parmi celles-ci, il est possible que nous en trouvions une "manifestement fausse". La question est alors : "d'où sort-elle?". La réponse n'est possible que si nous avons pris la précaution d'associer à chaque règle sa source : "NASA report 88-03-156, saisi par JMF le 12/3/97". On ira immédiatement vérifier la source, vérifier que la traduction est correcte.
Mais, avec le développement incrémental, il est possible que la règle en question soit le résultat de modifications successives. Il est fondamentalement important d'enregistrer celles-ci : "modifié par X le Y, pour telle raison". Dès lors, il devient possible de mettre le doigt sur l'origine de l'erreur. Et, par exemple, de se dire : "reprenons tout ce qui a été modifié par X, il a un point de vue complètement différent de notre objectif". Cela, moyennant une certaine discipline et quelques petits logiciels, est relativement facile, et rapporte extrèmement gros.
On peut également envisager des méta-connaissances du style : tel auteur commet fréquemment telle erreur.

7.5. Pourquoi pas?

Une autre question que l'on peut se poser face à un résultat insatisfaisant, est : "pourquoi n'a-t-il pas trouvé telle solution?". Cette question est beaucoup plus délicate, et n'a été abordée, à ma connaissance, que par très peu de chercheurs, dont Brigitte Saffar.

Chapitre précédent

Chapitre suivant