A propos d'intelligence artificielle...
Introduction empruntée à Henri Prade (Les livrets de service Culture UPS
3)
L'usage de l'expression Intelligence Artificielle (on utilisera le plus souvent l'abréviation IA dans la suite) s'est largement répandu dans le public, au fur et à mesure des progrès de la technologie informatique et de sa propagation dans les activités humaines. L'IA fait maintenant partie de notre culture comme en témoigne l'existence de nombreux articles, livres, ou films s'y rapportant plus ou moins directement.
Il est vrai que le terme Intelligence Artificielle a pu causer quelques malentendus, voire déplaire, et peut assurément être interprété de diverses manières. En effet, si chacun peut apprécier les capacités toujours plus grandes des machines pour effectuer des calculs numériques ou des opérations symboliques, ou traiter des documents, l'idée que la machine pourrait détenir ne serait-ce que quelques onces d'intelligence provoque bien naturellement des questions, des craintes et des fantasmes.
Comme le suggère le rapprochement, qui a pu sembler provocateur à certains, des mots "intelligence" et "artificiel", il s'agit de réussir à donner à des machines des capacités leur permettant d'effectuer des tâches ou des activités réputées intelligentes (car jusqu'à présent uniquement réalisées par des humains). Une telle définition reste cependant assez vague car elle ne donne ni une définition de l'intelligence, ni même ne précise la nature des capacités dont il convient de doter la machine. Ainsi, une machine capable de reclasser dans l'ordre croissant des nombres donnés en vrac, ou de résoudre des équations, n'est pas considérée comme intelligente pour autant (même si seulement un petit nombre de mathématiciens savent résoudre les équations considérées !).
Les recherches en IA tendent à rendre la machine capable d'acquérir de l'information, de raisonner sur une situation statique ou dynamique, de résoudre des problèmes combinatoires, de faire un diagnostic, de proposer une décision, un plan d'action, d'expliquer et de communiquer les conclusions qu'elle obtient, de comprendre un texte ou un dialogue en langage naturel, de résumer, d'apprendre, de découvrir. Pour ce faire, la machine doit être munie de méthodes génériques susceptibles de s'adapter à de larges classes de situations.
Même si sur toutes ces questions de grands progrès restent certainement à faire, de nombreux résultats ont déjà été obtenus montrant qu'au moins, dans une certaine mesure, ce programme est réalisable.
Cependant, une machine dotée de l'ensemble des fonctionnalités citées plus haut, ces fonctionnalités ayant atteint leur meilleur niveau d'efficience, serait encore assez loin de posséder les capacités de penser d'un être humain (même si la machine s'avérera bien plus performante sur certains registres de tâches qu'un être humain). On pourra consulter l'opuscule de la même série " Les machines pensent-elles " pour une discussion autour de cette question.
Par ailleurs, l'IA entretient des échanges fructueux avec les sciences
cognitives, car, d'une part elle fournit de nouveaux repères, points
de comparaison pour la compréhension de l'intelligence, et d'autre part
elle peut s'inspirer de ce que l'on sait du fonctionnement du cerveau et de
la façon dont l'homme raisonne, même si rien ne dit que l'IA doive
copier l'intelligence humaine dans toutes ses manières de procéder
(ainsi les avions volent, quoique différemment des oiseaux !). De
plus, puisque la machine doit échanger ses conclusions avec des usagers,
il importe qu'elle puisse s'exprimer en termes cognitivement significatifs pour
eux.
Petite histoire de l'IA
- Années 40-50 : travaux gravitant autour de l'idée de "machines
pensantes" : Warren Mc Culloch et Walter Pitts proposent les premiers
réseaux de neurones artificiels ; Norbert Wiener énonce des
mécanismes de communication et de contrôle pour les machines
comme pour les êtres vivants - la cybernétique- ; Claude Shannon
établit la théorie de l'information ; John von Neuman fonde
l'architecture des calculateurs (qui inspire toujours nos ordinateurs modernes
!); Alan Türing contribue de manière essentielle à la clarification
des fonctions calculables par machine (on lui doit également le fameux
"test de Tûring" qui proposait une façon "objective
de démontrer l'intelligence d'une machine : un homme converse - à
distance et par terminal interposé - avec une machine ; s'il croit
qu'il s'agit d'un autre homme alors la machine est réputée intelligente).
- Été 56 : acte de naissance de l'IA aux rencontres du Darmouth
College (Hanover, New Hampshire, USA ) organisées par John Mc Carthy
et Marvin Minsky. L'expression "Artificial Intelligence" est proposée
par John Mc Carthy.
- 1956 (encore) : Newell et Simon avec J. Cliff Shaw propose le premier programme
informatique capable de démontrer des théorèmes de logique.
A ce premier programme succèdera le célèbre "General
Problem Solver"
- depuis les années 60 ...: développement de programmes capables
de jouer aux échecs [Arthur Samuel et Alex Bernstein] ; Mackhack [Richard
Greenblatt] battait des joueurs expérimentés dès 1960!
Dans les années 70, Hans Berliner et d'autres dotent leurs programmes
de capacités d'évolution dynamique de leur comportement avec
l'évolution du jeu. Les progrès technologiques ont permis à
l'ordinateur d'explorer des combinatoires de plus en plus impressionnantes
et en 1997, Gary Kasparov est battu par "Deep Blue"...
- dans les années 60 et surtout 70, Thomas G. Evans et David Waltz
(pour ne retenir qu'eux) réalisent des programmes permettant de conceptualiser
des figures, d'exprimer des contraintes sur des formes géométriques,
etc.
- dès 1965, les chercheurs s'intéressent au "langage naturel".
Joseph Weizenbau réalise un programme simulant un dialogue qui peut
tromper (pas longtemps) un interlocuteur.
- en 1971, Terry Winograd exploite les possibilités de l'IA pour représenter
des morceaux de phrase pour les "comprendre" (monde des blocs).
- les années 70 et le début des années 80 voient le
développement de nombreux systèmes experts (Dendral en chimie,
Mycin en médecine, Hearsay-II en compréhension de la parole,
Prospector en géologie...).
- les années 80 et début 90 sont les années d'expérimentation
de robots mobiles capables de s'adapter à des environnements non complètement
connus (Rodney Brooks pour les travaux des années 80-90).
Après d'immenses espoirs fondés sur ces techniques, les années
90 ont connu un reflux important de la confiance dans l'exploitation pratique
des recherches réalisées. Les années 2000 montrent un regain
d'intérêt pour ces techniques maintenant maîtrisées
et donnant lieu à de multiples dévéloppement dans le domaine
de la gestion des connaissances.
Comme le montre ce bref aperçu historique, l'IA s'est largement développée
tout d'abord aux Etats-Unis, avant, à partir du milieu des années
70, d'intéresser des chercheurs en Europe puis en Asie. Pour ce qui est
de la France, si l'on excepte des pionniers de la cybernétique (Louis
Couffignal, Paul Braffort), et si l'on ne s'en tient qu'à des recherches
se réclamant explicitement de l'IA, les premières équipes
françaises dans ce domaine, furent créées à Paris,
puis à Marseille sous les impulsions respectives de Jacques Pitrat (qui
a en particulier mis en lumière le rôle des métaconnaissances
dans les processus de résolution de problèmes et d'apprentissage),
et d'Alain Colmerauer (père d'un langage de programmation, PROLOG, basé
sur la logique et très utilisé en IA). Des équipes d'IA
devaient ensuite bientôt naitre dans d'autres grands centres : Toulouse,
Grenoble, Nancy, … Aujourd'hui, presque tous les laboratoires d'informatique
comptent des chercheurs en IA.
1. Introduction aux Systèmes à Base de Connaissances
Un système à Base de Connaissances se distingue des systèmes
informatiques classiques par le fait qu'il tente d'exploiter explicitement des
"connaissances" sur un problème à résoudre pour
en faciliter la résolution. Bien entendu, cette approche est particulièrement
importante pour faire face à des problèmes "complexes".
Pour illustrer ce que nous entendons par un système complexe, nous vous
proposons d'explorer cette notion de complexité au travers d'exemples
concrets.
1.1. Illustration de la notion de complexité des algorithmes
et des problèmes
Soit à
écrire un programme qui calcule la somme des n premiers nombres entiers.
Un informaticien écrira : lire n
s <- 0
pour i variant de 1 à n
s <- s + i
finpour
imprimer s
La complexité de cet algorithme est O(n).
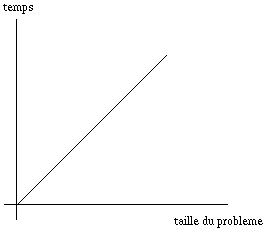
Un mathématicien écrira : lire n
imprimer (n * (n + 1) / 2)
La complexité de cet algorithme est O(1).
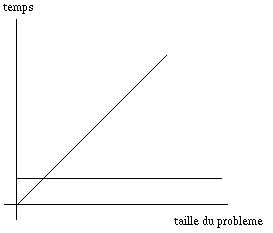
On ne peut pas faire mieux. C'est donc la
complexité de ce problème.
Soit maintenant à écrire un algorithme qui trie un tableau de nombres. Un débutant
écrira une boucle de 1 à n-1, au sein de laquelle il comparera deux cases successives,
en les permutant si elles ne sont pas dans l'ordre. Et il plongera cette boucle
dans une autre de 1 à n. La complexité de son algorithme sera O(n2).
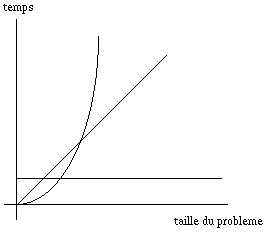
On montre qu'en fait, la complexité du problème est O(n
log(n)). 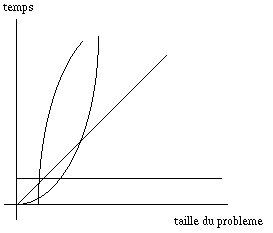
Soit
maintenant à écrire un programme qui joue un coup aux échecs. On développe
l'arbre de tous les coups possibles (alternativement coup ami et coup ennemi),
jusqu'à une profondeur n, puis on calcule une fonction d'évaluation sur
chaque feuille, et on remonte alternativement le max et le min des notes
obtenues. 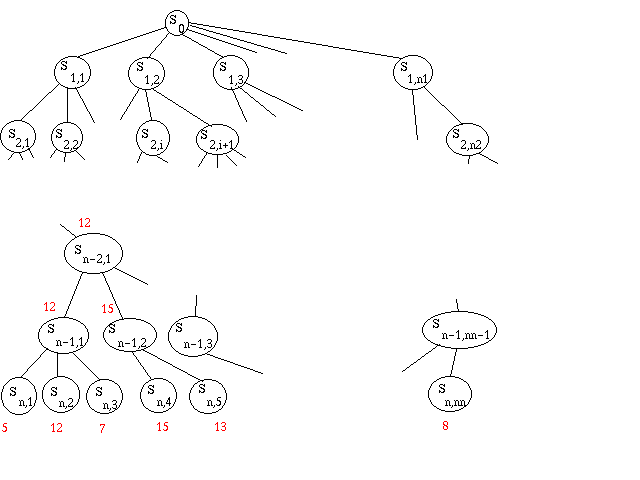
La complexité de cet algorithme est O(pn),
où p est le nombre moyen de coups légaux dans un état donné. 
Pour revenir un peu
sur terre, comparons n2 et 2n, pour n=100, en supposant
une micro-seconde par opération :
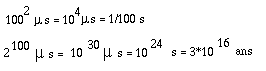
C'est-à-dire à peu près un million de fois l'age
de l'univers ! Inutile de chercher à acheter une machine mille fois ou un
million de fois plus rapide ; il faut abandonner l'espoir de résoudre le
problème.
1.2. Notion d'heuristique
Et pourtant... Je connais, et vous
connaissez aussi, des gens qui résolvent un tel problème en quelques minutes,
alors que leur "hardware" est environ 107 fois moins rapide que celui
d'un ordinateur. Donc, ils n'utilisent pas l'algorithme que nous avons évoqué au
paragraphe précédent. Qu'utilisent-ils? Ce que nous appellerons des
heuristiques, ou plus généralement des connaissances. Mettons les en évidence
sur un petit problème. Soit à résoudre le problème de cryptarithmétique : S E N D
M O R E
---------
M O N E Y
Il s'agit de trouver une bijection entre les lettres et des chiffres (S et
M ne pouvant être nuls) pour que l'addition soit correcte en base 10. Le seul
algorithme que je connaisse consiste à faire 8 boucles imbriquées de 0 à 9 pour
essayer toutes les valeurs possibles pour chacune des lettres : il est
typiquement exponentiel. Mais, grace à mes connaissances, je vais résoudre ce
problème en temps linéaire :
- Je commence par ré-écrire le problème :
D + E = Y + 10r1
r1 + N + R = E + 10r2
r2 + E + O = N + 10r3
r3 + S + M = O + 10r4
r4 = M
S # 0
M # 0
- Je considère l'équation la plus contrainte, r4 = M. Je sais que M ne peut
pas être nul, mais ça ne me suffit pas.
- Je démontre un lemme : une retenue ne peut être égale qu'à 0 ou 1.
- Donc M = 1, et r4 = 1.
- Je propage :
D + E = Y + 10r1
r1 + N + R = E + 10r2
r2 + E + O = N + 10r3
r3 + S + M = O + 10*1
r4 = M
M = 1
r4 = 1
S # 0
M # 0
- Je nettoie :
D + E = Y + 10r1
r1 + N + R = E + 10r2
r2 + E + O = N + 10r3
r3 + S = O + 9
M = 1
S # 0
- Je prends l'équation la plus contrainte, r3 + S = O + 9. r3 + S vaut au
maximum 10, O ne peut pas valoir 1 (valeur déjà prise par M), donc O = 0.
- Je propage et je nettoie :
D + E = Y + 10r1
r1 + N + R = E + 10r2
r2 + E = N + 10r3
r3 + S = 9
O = 0
M = 1
- De deux choses l'une : r3 = 0 et S = 9, ou r3 = 1 et S = 8. Mais si je
commence comme ça, je vais me retrouver avec un processus combinatoire. Donc
je refuse cette solution de facilité. Je regarde l'équation r2 + E = N + 10r3.
- r2 + E vaut au plus 10, et N ne peut valoir 0. Donc r3 = 0, et S = 9.
- Je propage et je nettoie :
D + E = Y + 10r1
r1 + N + R = E + 10r2
r2 + E = N
S = 9
O = 0
M = 1
- Puisque je cherche une bijection, je ne peux pas avoir E = N, donc r2 =1.
D + E = Y + 10r1
r1 + N + R = E + 10
1 + E = N
S = 9
O = 0
M = 1
- Je considère le couple d'équations 1 + E = N et r1 + N + R = E + 10. Je
peux ré-écrire :
r1 + 1 + E + R = E + 10, ou
r1 + R = 9
R ne peut pas valoir 9 (valeur de S), donc R = 8 et r1 = 1.
- Je propage et je nettoie :
D + E = Y + 10
1 + E = N
R = 8
S = 9
O = 0
M = 1
- Arrivé là, je ne vois plus d'astuce. Je vais raisonner, non plus sur le
problème, mais sur moi : si je m'obstine à ne pas vouloir faire de
combinatoire, peut-être ne trouverai-je jamais la solution ; par contre, si
j'accepte de faire un petit peu de combinatoire, je trouverai la solution en
au plus 46 essais (il me reste 4 inconnues, prenant leurs valeurs
dans [2 3 4 5 6 7]).
- Allons y, mais astucieusement. Y + 10 est au moins égal à 12. N et E sont
très fortement liés. De deux choses l'une : soit D < E, soit N < D.
- Premier cas : puisque je veux au moins 12, commençons par les plus grandes
valeurs possibles : N = 7, E = 6, D = 5 ; cela fait D + E = 11, insuffisant ;
inutile d'essayer des valeurs plus petites. La moitié de la combinatoire est
déjà éliminée.
- Reste l'hypothèse D = 7, N = 6, E = 5. Ca marche. Mais c'est limite (12),
donc inutile d'essayer d'autres cas.
J'ai donc résolu en temps
quasi-linéaire un problème pour lequel le seul algorithme connu est exponentiel.
Miracle? Non :
|
algorithme |
heuristiques |
| temps de calcul |
10n |
n + epsilonn |
| taille du programme |
3n |
? |
La taille du "programme " que j'ai utilisé se
mesure probablement en téra-octets. Peut-on écrire, et maintenir, un tel
programme? Non.
1.3. Développement incrémental
Les connaissances que nous
mettons en oeuvre pour résoudre des problèmes sont de deux ordres : les
connaissances "noir sur blanc", qu'on trouve par exemple dans les livres, et les
connaissances "matière grise". Ces dernières ont la particularité d'être
inexprimables, dans la mesure où la personne qui les détient ne sait pas
qu'elle les détient. Si par exemple vous demandez à un bon joueur comment il
a trouvé tel coup génial, il vous répondra probablement : <<Bein, euh...
je ne sais pas ; j'ai regardé l'échiquier, et il m'a semblé qu'il n'y avait rien
d'autre à faire>>.
La situation est donc déséspérée? Non, car ces
connaissances ne sont pas innées, elles ont été acquises. Reste à identifier le
mécanisme d'acquisition. Pour ce faire, comparons le transfert de la
connaissance entre un enseignant et ses étudiants, avec le transfert entre un
"maitre" et son apprenti.
| noir sur blanc |
matière grise |
| peu de temps |
tout son temps |
| structuré |
cas par cas |
| pratiquement pas de retour |
feedback |
| information positive |
information négative |
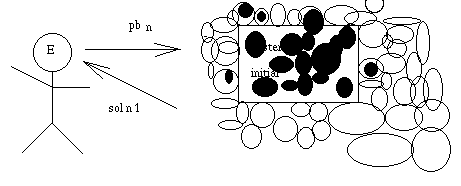
Nous allons donc nous inspirer
de ce processus pour développer notre système. Dans un premier temps,
l'"ingénieur de la connaissance" (bof) discute avec l'"expert". Il construit un
système initial. 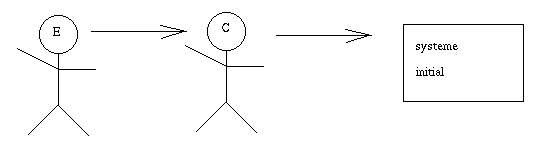
L'"expert" soumet un
premier problème au système, et analyse la solution. 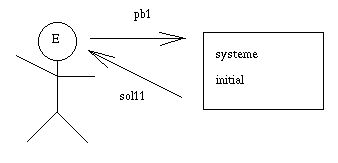
Le "cogniticien" (beurk) modifie le système :
ajout de connaissances, suppression de choses qui avaient été mal
comprises.
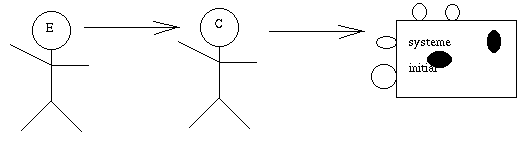
On recommence.
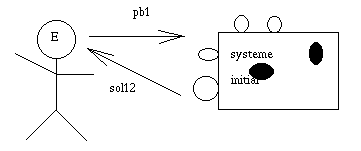
Même ce qui vient d'être ajouté est remis en
question. 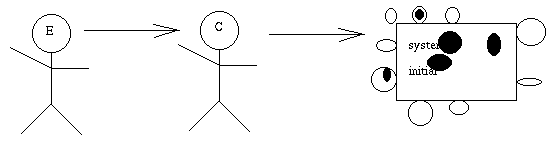
Et on continue ainsi jusqu'à
ce que, en moyenne, la solution à n'importe quel problème soit jugée
acceptable.
Le processus a convergé,
on a capturé la connaissance.
Sauf que ce procédé est impraticable : une
étude commandée en 1972 par le DoD a montré que, s'il fallait $75 pour écrire
une instruction, il en fallait 4000 pour modifier une instruction. Or ici, la
quasi totalité du programme résulte de modifications.
1.4. Représentations déclaratives
Que faire? Rendre les
modifications moins couteuses. D'où vient le coût? Du fait que le programme est
structuré, donc que lorsqu'on veut modifier une instruction il faut prendre
toutes les autres en compte, et répercuter la modification en de nombreux
endroits. Ce qu'il faudrait, ce serait pouvoir exprimer les connaissances de
manière déclarative, c'est-à-dire indépendamment de leur mode d'emploi, pouvoir
dire le "quoi" sans se préoccuper du "comment".
Par analogie avec la
Thermodynamique, un programme classique a une faible entropie, alors qu'on en
veut une très grande ; au lieu d'un cristal, on voudrait un programme
"gazeux".
Il existe un langage qui permet cela, connu depuis 2400 ans, qui
s'appelle la Logique. C'est pour cette raison que nous allons étudier la
Logique, ou plus exactement les Logiques.
 Chapitre suivant
Chapitre suivant  Table des matières
Table des matières
© Jean-Marc Fouet,
Juillet 1999
Attention, ce fichier n'est peut-être plus d'actualité s'il est dans votre cache
; vérifiez la date du copyright, et faites éventuellement un 'reload'.
©
Jean-Marc Fouet, 18-11-1999 





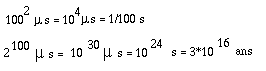




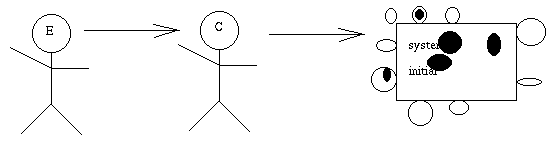

 Chapitre suivant
Chapitre suivant  Table des matières
Table des matières