![]()
|
Sommaire : |
Numérisation
de l'information Le texte L'image fixe Le son et la vidéo La protection contre les erreurs |
![]()
L'information existe sous des formes diverses. Pour la manipuler et, en particulier, la transporter, on est amené à la coder.
| parole
: système : téléphone codeur : microphone décodeur : écouteur transmission : signaux analogiques et numériques |
image fixe : |
données informatiques : |
télévision : |
De nos jours, l'information est souvent présentée dans des documents composites, comme une page Web, où simultanément peuvent être présentés un texte, une image fixe, un clip vidéo,.... . L'information est, en effet, présentée sous forme multimédia. Chaque type d'information possède son système de codage, mais le résultat est le même : une suite de 0 et de 1. Le transport de l'information consiste alors à transmettre des bits, quelque soit la signification du train de bits transmis.
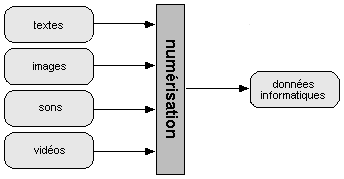
Dans les paragraphes qui suivent, on examinera comment il est possible de numériser chaque média.
![]()
Le premier code relatif au texte est certainement le code Morse, en service bien avant l'utilisation de l'ordinateur. Et pourtant, il s'agit bien d'un code binaire qui aurait pu servir à numériser les textes, puisqu'il est composé de deux symboles seulement : le point et le trait (on pourrait aussi bien dire 0 et 1).
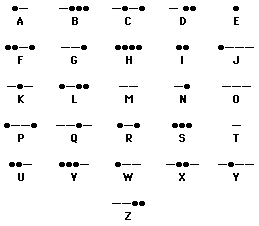
Malheureusement, il souffre de deux inconvénients majeurs :
il est "pauvre" : peu de caractères peuvent être codés ;
il utilise des combinaisons de traits et de points de longueur variable ce qui n'est pas commode, notamment pour la numérisation d'éléments ayant des probabilités d'apparition de même ordre.
Pour ces raisons, il n'a pas été utilisé pour le codage numérique de l'information (apparemment, on n'y a peut-être pas pensé !) ; toutefois, compte tenu de son utilisation passée, il méritait d'être mentionné.
Si on se fixe comme règle de trouver un code permettant de représenter numériquement chaque caractère de manière à obtenir un nombre de bits fixe, il est simple de comprendre qu'avec un code à p positions binairs on pourra représenter 2p caractères. Effectivement, dans le passé, on a utilisé de tels codes, généralement en les définissant par des tables, le code étant divisé en poids faibles et en poids forts :
![]() :
:
code à 5 positions : un de ses représentants est ATI (Alphabet Télégraphique International, utilisé par le Télex)
code à 6 positions : ISO6 (ce code très employé sur les premiers ordinateurs est aujourd'hui abandonné)
code à 7 positions : ASCII : la panacée universelle
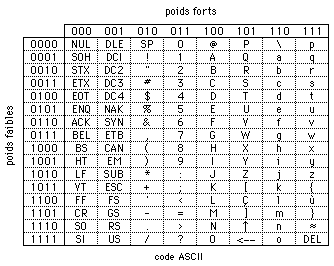
ce code fait apparaître des caractères non imprimables appelés caractères de manœuvre qui provoquent des actions sur des dispositifs informatiques ou qui transportent de l'information de service. Par exemple, FF signifie "passage à la page suivante" ce qui pour une imprimante est une information indispensable.
code à 8 positions : ASCII étendu, EBCDIC
Le code ASCII est un code sur 7 positions ; comme les ordinateurs stockent l'information dans des mots dont la longueur est un multiple de 8 bits (octets), on complète généralement le code ASCII par un "0" en tête pour former un octet. On peut aussi utiliser ce degré de liberté supplémentaire pour définir des alphabets spéciaux ; dans ce cas, on avertit en mettant un "1" en tête à la place du "0" ce qui correspond au code ASCII étendu ; malheureusement, il y a plusieurs codes ASCII étendus car il n'y a pas encore de normalisation imposée ce qui rend difficile mais pas insurmontable le passage d'un document d'une plate-forme à une autre.
Le code EBCDIC est d'emblée un code sur 8 bits ce qui permet d'obtenir 256 caractères représentables contre 128 pour le code ASCII. Il a été utilisé par IBM pour le codage de l'information sur ses machines. Il n'a pas atteint toutefois la popularité du code ASCII.
code à 16 positions : Unicode
Ce code est récent et a été mis en oeuvre pour satisfaire tous les usagers du Web. Il incorpore presque tous les alphabets existants (Arabic, Armenian, Basic Latin, Bengali, Braille, Cherokee, etc....) ; il est compatible avec le code ASCII. Par exemple le caractère latin A est codé 0x41 en ASCII et U+0041 en Unicode ; le caractère monétaire € est codé 0x80 en ASCII étendu et U+20AC en Unicode.
Exercices et tests : QCM14
![]()
L'image numérique est usuellement une image décrite en termes de lignes et chaque ligne en terme de points. Une image VGA de résolution 640x480 signifie que l'image est une matrice de 480 lignes, chaque ligne comportant 640 points ou pixels. Une image est alors représentée par un fichier donnant la liste des points ligne par ligne, colonne par colonne.
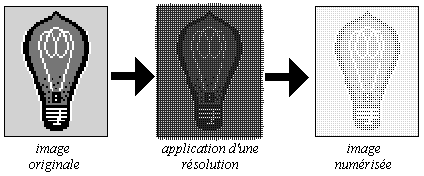
Un pixel est codé suivant la qualité de l'image :
image en noir et blanc (image binaire) : un seul bit suffit pour coder le point (0 pour noir, 1 pour blanc) ;
image en 256 nuances de gris : chaque point est représenté par un octet (8 bits) ;
image en couleur : on montre que la couleur peut être exprimée comme une combinaison linéaire de trois couleurs de base, par exemple Rouge(R), Vert(V), Bleu(B). Ainsi une couleur quelconque x est exprimée comme
x = aR + bV +cB
où a, b, c sont des doses de couleurs de base. Usuellement, une bonne image correspond à des doses allant de 0 à 255. Par suite une image couleur de ce type peut être représentée par 3 matrices (une par couleur de base) dont chacune d'elle possède des éléments sur 8 bits, ce qui au total fait 24 bits par pixel.
On se rend vite compte du volume atteint pour des images importantes et de bonne définition. Une image 640x480 en couleur (24 bits) occupe un volume de 921 600 octets. On est alors amené à utiliser des techniques de compression pour réduire la taille des fichiers d'images. Une des premières techniques est l'emploi de codes de Huffman qui emploie des mots codés de longueur variable : long pour les niveaux de couleur rares, court pour les niveaux de couleur fréquents. Ce type de codage est dit sans perte puisque la compression ne dénature pas l'information. D'autres méthodes permettent d'obtenir des résultats plus performants en terme de réduction de volume ; dans cette catégorie, dite compression avec perte, des détails peu pertinents de l'image disparaissent ; c'est notamment le cas du standard JPEG qui utilise des transformations en cosinus discrets appliquées à des sous-images.
![]()
Les données de type son et vidéo sont à l'origine analogique sous forme de signaux (un ou deux signaux pour le son, 3 signaux pour la vidéo-image). Ces signaux analogiques sont numérisés de la manière suivante :
| 1 - Échantillonnage Le signal est échantillonné : à une fréquence donnée f, on mesure la hauteur du signal. On obtient alors une séquence de mesures. |
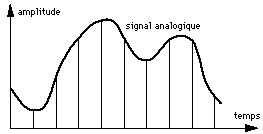 |
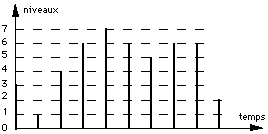 |
2 - Quantification On se fixe une échelle arbitraire de valeurs (usuellement suivant une puissance de 2: 2p valeurs) et on fait correspondre chaque mesure à une valeur dans cette échelle. on est évidemment conduit à faire des approximations ce qui correspond à un bruit dit de quantification |
| 3- Codage Chaque valeur est transformée en sa combinaison binaire, la suite de ces combinaisons étant placée dans un fichier. 011001100110111110101110110010...... |
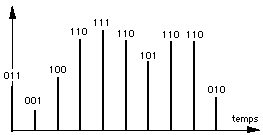 |
Le volume des fichiers obtenus après numérisation dépend crucialement de la fréquence d'échantillonnage f et de la valeur de p (longueur du codage de chaque valeur). La fréquence d'échantillonnage, en particulier, ne peut être choisie arbitrairement. Les résultats en traitement de signal indiquent que la fréquence d'échantillonnage d'un signal doit au moins être le double de la plus grande des fréquences du signal (c'est à dire la plus grande de toutes celles des composantes sinusoïdales - développement de Fourier - composant le signal).
exemple : la parole est transmise usuellement par le réseau téléphonique. Elle correspond à des signaux analogiques dont la fréquence varie entre 300 Hz et 3400 Hz. La plus grand des fréquences est donc 3400 Hz que l'on arrondit à 4000 Hz par précaution. La fréquence d'échantillonnage doit donc être au moins de 8000 Hz. Si l'on choisit cette fréquence d'échantillonnage et si l'on décide de coder sur 8 bits chaque échantillon (cela est suffisant pour le parole), on obtient pour une seconde de parole un volume de 64 000 bits ; une transmission en temps réel de la parole nécessite donc des liaisons à un débit de 64 Kbits/s. C'est notamment le cas du RNIS français (Numéris) qui propose des canaux à 64 Kbits/s.
Comme dans le cas de l'image fixe, mais de manière extrêmement amplifiée, les volumes obtenus sont considérables et il est nécessaire, pour leur stockage comme pour leur transport, de les compresser. Les techniques diffèrent ici, suivant que l'on a un fichier son ou un fichier vidéo.
Pour le son, le système de codage explicité plus haut (codage sur n bits de chaque échantillon) est appelé PCM (Pulse Code Modulation). Il est possible de réduire le volume avec les codages suivants :
La problématique du son (et aussi de la vidéo) est une transmission en "temps réel" ; il est donc nécessaire d'utiliser des systèmes de codage ou codecs performants. Les codecs audio sont décrits par des normes standards de l'ITU dont voici quelques exemples :
codec G.711 : algorithme de codage : PCM ; échantillonnage à 8 KHz, débit nécessité : 64 Kbits/s ;
codec G.722 : algorithme de codage : ADPCM ; échantillonnage à 7 KHz ; débit nécessité : 64 Kbits/s ;
codec G.723 : algorithmes de codage MP-MLQ (MultiPulse Maximum Likelihood Quantization) et ACELP (Agebraic Code-Excited Linear Prediction) ; échantillonnage à 8 KHz ; débit nécessité entre 5,3 et 6,3 Kbits/s ;
Pour la vidéo, divers procédés de codage sont employés dans le but de réduire le volume des fichiers. Le plus connu correspond à la série de normes MPEG. Le principe de compression s'appuie sur trois types d'images :
les images "intra" sont des images peu compressées qui servent de repère (une image intra pour 10 images successives) ;
les images "prédites" sont des images obtenues par codage et compression des différences avec les images intra ou prédites précédentes (une image prédite toutes les trois images) ;
les images "interpolées" sont calculées comme images intermédiaires entre les précédentes.
L'utilisation de vidéos numériques MPEG nécessite la présence d'une carte de décompression dans le micro-ordinateur d'exploitation. Les principaux standards sont MPEG1 (débit nécessité : 1,5 Mbits/s), MPEG2 (débit nécessité : 4 à 10 Mbits/s), MPEG4 (débit nécessité : 64 Kbits/s à 2 Mbits/s).
Exercices et tests : Exercice 15, Exercice 21, Exercice 35, Exercice 40, QCM21
![]()
Lors de la transmission d'un train de bits, des erreurs peuvent se produire, c'est à dire qu'un "1" peut être transformé en un "0" ou réciproquement.
On définit le taux d'erreur par le rapport :
![]()
L'ordre de grandeur du taux d'erreur est de 10-5 à 10-8. Suivant le type d'application, une erreur peut avoir des conséquences importantes et c'est pourquoi il convient souvent de mettre en oeuvre des dispositifs permettant de détecter les erreurs et si possible de les corriger. Il convient de noter à ce sujet que le taux d'erreur dépend de la qualité du support de transmission (notamment son immunité au bruit).
Les statistiques indiquent que 88% des erreurs proviennent d'un seul bit erroné, c'est à dire que ce bit erroné est entouré de bits corrects ; 10% des erreurs proviennent de deux bits adjacents erronés. On voit donc que le problème prioritaire à résoudre est la détection d'un seul bit erroné et, si possible, sa correction automatique.
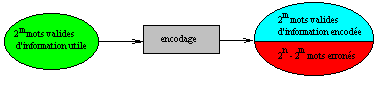
Dans cet ordre d'idées, on utilise des codes détecteurs d'erreurs : l'information utile est encodée de manière à lui ajouter de l'information de contrôle ; le récepteur effectué le décodage et à l'examen de l'information de contrôle, considère que l'information est correcte ou erronée ; dans le dernier cas, une demande de répétition de la transmission est effectuée.
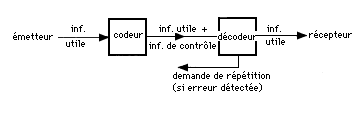
Les codes détecteurs d'erreurs se classent en 2 catégories :
codes en bloc : l'information de contrôle et l'information utile forment un tout consistent. Si le bloc est composé de deux partie distinctes (information utile et information de contrôle) le code est dit systématique.

codes convolutionnels ou récurrents : la détection des erreurs dans un bloc dépend des blocs précédents. Ils ne seront pas étudiés ici.
Une notion importante dans la recherche de codes détecteurs ou correcteurs est celle de distance de Hamming. Considérons une information utile constituée de mots de m bits : on peut donc construire 2m mots distincts au total. Définissons l'information de contrôle sous la forme de r bits déduis de manière unique à partir des m bits utiles . L'information "habillée" en résultant est constituée de n=m+r bits et , compte-tenu de l'unicité de la définition des bits de contrôle, on a au total 2m mots valides de n bits. Cependant, avec n bits, on peut avoir 2n mots différents. La différence 2n-2m indique le nombre de mots erronés.
La distance de Hamming de deux mots : d(m1, m2) est le nombre de bits différents de même rang
exemple : m1 = 10110010 m2 = 10000110 d(m1,m2) = 3
2 mots de code seront d'autant moins confondus que leur distance de Hamming sera plus grande ; on peut définir une distance minimum dmin ; si d(m1, m2) < dmin, alors m2 est une copie erronée de m1.
| mi et mj sont des mots du code ; m'i est une copie erronée de mi |
|
d'où la règle 1 : Pour détecter p erreurs, il faut que dmin > p
|
exemple : détection des erreurs simples : dmin>2
Intéressons-nous maintenant à la correction des erreurs jusqu'à un ordre q ; chaque mot de code et ses copies "admissibles" doivent être dans des sphères non sécantes :
| mi et mj sont des mots du code ; m'i est un mot erroné qui doit être assimilé à mi. |
|
d'où la règle 2 : Pour corriger des erreurs jusqu'à l'ordre q, il faut que dmin > 2q |
exemple : la correction des erreurs simples nécessite dmin > 2
Un code linéaire est un code en bloc systématique (n,m) dans lequel les r = n - m
bits de contrôle dépendent linéairement des m bits d'information. Soit l'information utile
représentée par le vecteur ligne ![]() ; l'information codée
est représentée par le vecteur ligne
; l'information codée
est représentée par le vecteur ligne ![]() avec
avec
| y1 = x1 | y2 = x2 | ...... | ym = xm | ym+1 = a1 | ym+2 = a2 | ..... | y m+r = a r |
où les ai sont les
bits de contrôle, donc ![]() .
.
Le code est alors simplement défini par
la relation matricielle ![]() où G est la matrice génératrice du code. La forme
générale de G est :
où G est la matrice génératrice du code. La forme
générale de G est :

d'où les bits de contrôle : ai = x1g1i + x2g2i+ .... + xmgmi.
exemple : code (6,3) avec
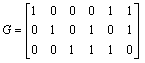
information utile : ![]() donc 8 mots possibles
donc 8 mots possibles
information codée : ![]()
La relation ![]() conduit à
conduit à
a1 = x2 + x3
a2 = x1 + x3
a3 = x1 + x2
Les mots du code sont :
| 000000 | 001110 | 010101 | 011011 |
| 100011 | 101101 | 110110 | 111000 |
On constate que dmin = 3 ce qui permet la correction des erreurs simples et la détection des erreurs doubles
exemple : code (8,7) avec
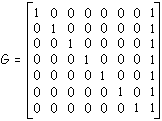
information utile : ![]()
information codée : ![]()
La relation ![]() conduit à a1 = x1 + x2 + x3 + x4
+ x5 + x6 + x7 (modulo 2)
conduit à a1 = x1 + x2 + x3 + x4
+ x5 + x6 + x7 (modulo 2)
a1 est appelé bit de parité : les mots du code ont un nombre pair
de 1.
On pourra ainsi représenter des caractères sur 8 bits avec 7 bits relatifs au code ASCII et le huitième bit étant le bit de parité (que l'on peut placer, bien sûr, où l'on veut ; la coutume est de le placer en tête) :
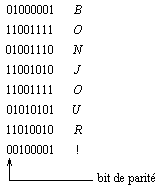
Avec ce système, 2 caractères différant par 1 du code ASCII diffèrent aussi par le bit de parité donc dmin = 2. Ce code ne permet donc que la détection des erreurs simples. On peut améliorer la protection contre les erreurs en effectuant également un contrôle de parité "longitudinal" par opposition au contrôle de parité précédent appelé "vertical" (LRC = Longitudinal Redundancy Check ; VRC = Vertical Redundancy Check) en ajoutant un caractère de contrôle tous les b blocs :
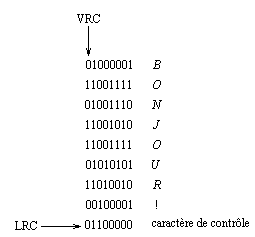
La transmission série des blocs sera donc :
| 01100000 | 00100001 | ------------ | 11001111 | 01000010 | --------> |
| contrôle | ! | O | B |
Avec ce système, deux groupes de blocs différant par 1 bit d'information utile diffèrent aussi par le bit VRC, par le bit LRC et par le bit LRC+VRC. On a donc dmin = 4 ce qui permet la détection des erreurs simples et doubles et la correction des erreurs simples.
Les codes polynômiaux sont des codes linéaires systématiques qui permettent la détection des erreurs. Ils sont très utilisés dans les procédures actuelles de transmission de données. Soit un message de m bits utiles :
![]()
où la numérotation des bits est quelque peu différente de celle utilisée jusqu'à présent (mais traditionnelle dans l'utilisation des codes polynômiaux).. Au message X, on associe le polynôme :
X(z) = x0 + x1 z + x2z2 + .....+ xm-1 zm-1
De tels polynômes peuvent être ajoutés (modulo 2) et multipliés suivant les règles booléennes. Un code polynomial est un code linéaire systématique tel que chaque mot du code est représenté par des polynômes Y(z) multiples d'un polynôme H(z) appelé polynôme générateur :
Y(z) = Q(z).H(z)
Examinons comment on passe de l'information utile (m bits) représentée par un polynôme X(z) à l'information codée (n bits) représentée par le polynôme Y(z). On définira donc un code polynomial (n,m) et on ajoutera à l'information utile r = n-m bits de contrôle. On pose :
X(z) = x0
+ x1 z + x2z2 + .....+ xm-1 zm-1
H(z) = h0 + h1z + h2z2 + ...... + zr polynôme générateur de degré r
Le polynôme zr X(z) est un polynôme de degré m + r - 1 = n - 1. Il comporte n termes dont les r premiers sont nuls. Effectuons la division polynomiale de zr X(z) par H(z) :
zr X(z) = Q(z).H(z) + R(z)
où R(z) est un polynôme de degré r-1, reste de la division. Puisque l'addition modulo 2 est identique à la soustraction modulo 2, on a
Y(z) = Q(z).H(z) = zr X(z) + R(z)
Y(z) est le polynôme associé au mot-code. Il comporte n termes et est de degré n-1.
exemple : code polynomial (7,4), de polynôme générateur H(z) = 1 + z + z3. Une information utile correspond au polynôme X(z) = x0 + x1z + x2z2 + x3z3. La division de zr X(z) par H(z) conduit aux résultats suivants :
Q(z) = x3z3
+ x2z2 +(x1 + x3)z + x0 + x2
+ x3
R(z) = (x1 + x2 + x3)z2 + (x0 + x1
+ x2)z + x0 + x2 + x3
Y(z) = x3z6 + x2z5 + x1z4
+ x0z3 + (x1 + x2 + x3)z2
+ (x0 + x1 + x2)z + x0 + x2 + x3
d'où le mot de code (x3 x2 x1 x0 a2 a1 a0) avec
a2 = x1
+ x2 + x3
a1 = x0 + x1 + x2
a0 = x0 + x2 + x3
d'où la matrice G du code
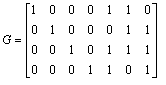
Les principaux codes polynomiaux utilisés en téléinformatique sont :
cas particulier : Un code cyclique est un code polynomial (n,m) tel que son polynôme générateur H(z) divise zn + 1
zn + 1 = H(z)W(z)
où W(z) est un polynôme de degré n. Les codes cycliques possèdent la propriété fondamentale suivante : une permutation circulaire d'un mot du code est un mot du code.
Exercices et tests : Exercice 22, Exercice 23, Exercice 24, Exercice 25, Exercice 26, Exercice 27, Exercice 28, Exercice 29, Exercice 30, Exercice 31, QCM24, QCM25, QCM26, QCM27, QCM28, QCM29, QCM30
![]()