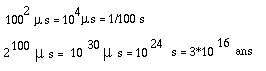1) Systèmes à Base de Connaissances
Un système à Base de Connaissances se distingue des systèmes
informatiques classiques par le fait qu'il tente d'exploiter explicitement des
"connaissances" sur un problème à résoudre pour
en faciliter la résolution. Bien entendu, cette approche est particulièrement
importante pour faire face à des problèmes "complexes".
Pour illustrer ce que nous entendons par un système complexe, nous vous
proposons d'explorer cette notion de complexité au travers d'exemples
concrets.
1.1. Complexité des algorithmes et des problèmes
Soit à
écrire un programme qui calcule la somme des n premiers nombres entiers.
Un informaticien écrira : lire n
s <- 0
pour i variant de 1 à n
s <- s + i
finpour
imprimer s
La complexité de cet algorithme est O(n).
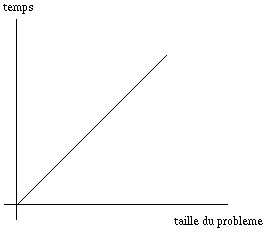
Un mathématicien écrira : lire n
imprimer (n * (n + 1) / 2)
La complexité de cet algorithme est O(1).
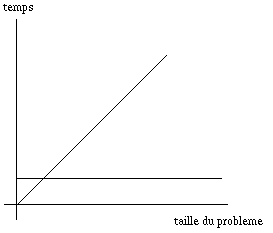
On ne peut pas faire mieux. C'est donc la complexité de ce problème.
Soit maintenant à écrire un algorithme qui trie un tableau de nombres. Un débutant
écrira une boucle de 1 à n-1, au sein de laquelle il comparera deux cases successives,
en les permutant si elles ne sont pas dans l'ordre. Et il plongera cette boucle
dans une autre de 1 à n. La complexité de son algorithme sera O(n2).
On montre qu'en fait, la complexité du problème est O(n log(n)). 
Soit maintenant à écrire un programme qui joue un coup aux échecs. On développe
l'arbre de tous les coups possibles (alternativement coup ami et coup ennemi),
jusqu'à une profondeur n, puis on calcule une fonction d'évaluation sur
chaque feuille, et on remonte alternativement le max et le min des notes obtenues.
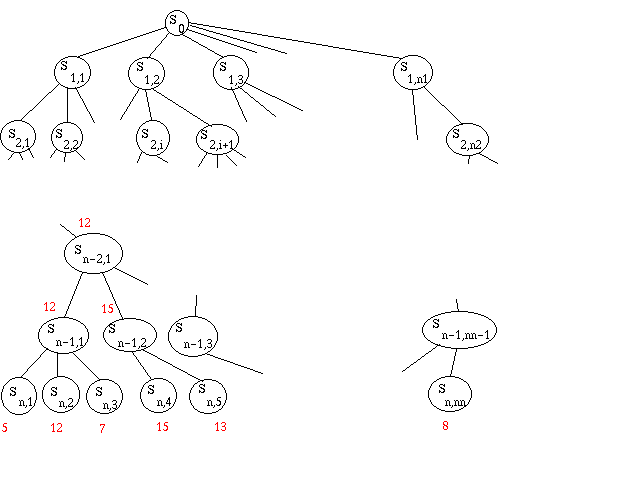
La complexité de cet algorithme est O(pn),
où p est le nombre moyen de coups légaux dans un état donné. 
Pour revenir un peu sur terre, comparons n2 (n au carré) et 2n (2
à la puissance n), pour n=100, en supposant une micro-seconde par
opération :
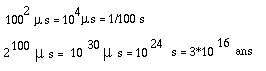
C'est-à-dire à peu près un million de fois l'age de l'univers ! Inutile de chercher
à acheter une machine mille fois ou un million de fois plus rapide ; il faut
abandonner l'espoir de résoudre le problème.
1.2. Notion d'heuristique
Et pourtant... Je connais, et vous connaissez aussi, des gens qui résolvent
un tel problème en quelques minutes, alors que leur "hardware" est environ 107
fois moins rapide que celui d'un ordinateur. Donc, ils n'utilisent pas l'algorithme
que nous avons évoqué au paragraphe précédent. Qu'utilisent-ils? Ce que nous
appellerons des heuristiques, ou plus généralement des connaissances. Mettons
les en évidence sur un petit problème. Soit à résoudre le problème de cryptarithmétique
:
S E N D
M O R E
---------
M O N E Y
Il s'agit de trouver une bijection entre les lettres et des chiffres (S et
M ne pouvant être nuls) pour que l'addition soit correcte en base 10. Le seul
algorithme que je connaisse consiste à faire 8 boucles imbriquées de 0 à 9 pour
essayer toutes les valeurs possibles pour chacune des lettres : il est
typiquement exponentiel. Mais, grace à mes connaissances, je vais résoudre ce
problème en temps linéaire :
- Je commence par ré-écrire le problème :
D + E = Y + 10r1
r1 + N + R = E + 10r2
r2 + E + O = N + 10r3
r3 + S + M = O + 10r4
r4 = M
S # 0
M # 0
- Je considère l'équation la plus contrainte, r4 = M. Je sais que M ne peut
pas être nul, mais ça ne me suffit pas.
- Je démontre un lemme : une retenue ne peut être égale qu'à 0 ou 1.
- Donc M = 1, et r4 = 1.
- Je propage :
D + E = Y + 10r1
r1 + N + R = E + 10r2
r2 + E + O = N + 10r3
r3 + S + M = O + 10*1
r4 = M
M = 1
r4 = 1
S # 0
M # 0
- Je nettoie :
D + E = Y + 10r1
r1 + N + R = E + 10r2
r2 + E + O = N + 10r3
r3 + S = O + 9
M = 1
S # 0
- Je prends l'équation la plus contrainte, r3 + S = O + 9. r3 + S vaut au
maximum 10, O ne peut pas valoir 1 (valeur déjà prise par M), donc O = 0.
- Je propage et je nettoie :
D + E = Y + 10r1
r1 + N + R = E + 10r2
r2 + E = N + 10r3
r3 + S = 9
O = 0
M = 1
- De deux choses l'une : r3 = 0 et S = 9, ou r3 = 1 et S = 8. Mais si je
commence comme ça, je vais me retrouver avec un processus combinatoire. Donc
je refuse cette solution de facilité. Je regarde l'équation r2 + E = N + 10r3.
- r2 + E vaut au plus 10, et N ne peut valoir 0. Donc r3 = 0, et S = 9.
- Je propage et je nettoie :
D + E = Y + 10r1
r1 + N + R = E + 10r2
r2 + E = N
S = 9
O = 0
M = 1
- Puisque je cherche une bijection, je ne peux pas avoir E = N, donc r2 =1.
D + E = Y + 10r1
r1 + N + R = E + 10
1 + E = N
S = 9
O = 0
M = 1
- Je considère le couple d'équations 1 + E = N et r1 + N + R = E + 10. Je
peux ré-écrire :
r1 + 1 + E + R = E + 10, ou
r1 + R = 9
R ne peut pas valoir 9 (valeur de S), donc R = 8 et r1 = 1.
- Je propage et je nettoie :
D + E = Y + 10
1 + E = N
R = 8
S = 9
O = 0
M = 1
- Arrivé là, je ne vois plus d'astuce. Je vais raisonner, non plus sur le
problème, mais sur moi : si je m'obstine à ne pas vouloir faire de
combinatoire, peut-être ne trouverai-je jamais la solution ; par contre, si
j'accepte de faire un petit peu de combinatoire, je trouverai la solution en
au plus 46 essais (il me reste 4 inconnues, prenant leurs valeurs
dans [2 3 4 5 6 7]).
- Allons y, mais astucieusement. Y + 10 est au moins égal à 12. N et E sont
très fortement liés. De deux choses l'une : soit D < E, soit N < D.
- Premier cas : puisque je veux au moins 12, commençons par les plus grandes
valeurs possibles : N = 7, E = 6, D = 5 ; cela fait D + E = 11, insuffisant ;
inutile d'essayer des valeurs plus petites. La moitié de la combinatoire est
déjà éliminée.
- Reste l'hypothèse D = 7, N = 6, E = 5. Ca marche. Mais c'est limite (12),
donc inutile d'essayer d'autres cas.
J'ai donc résolu en temps
quasi-linéaire un problème pour lequel le seul algorithme connu est exponentiel.
Miracle? Non :
|
algorithme |
heuristiques |
| temps de calcul |
10n |
n + epsilonn |
| taille du programme |
3n |
? |
La taille du "programme " que j'ai utilisé se
mesure probablement en téra-octets. Peut-on écrire, et maintenir, un tel
programme? Non.
1.3. Développement incrémental
Les connaissances que nous
mettons en oeuvre pour résoudre des problèmes sont de deux ordres : les
connaissances "noir sur blanc", qu'on trouve par exemple dans les livres, et les
connaissances "matière grise". Ces dernières ont la particularité d'être
inexprimables, dans la mesure où la personne qui les détient ne sait pas
qu'elle les détient. Si par exemple vous demandez à un bon joueur comment il
a trouvé tel coup génial, il vous répondra probablement : <<Bein, euh...
je ne sais pas ; j'ai regardé l'échiquier, et il m'a semblé qu'il n'y avait rien
d'autre à faire>>.
La situation est donc déséspérée? Non, car ces
connaissances ne sont pas innées, elles ont été acquises. Reste à identifier le
mécanisme d'acquisition. Pour ce faire, comparons le transfert de la
connaissance entre un enseignant et ses étudiants, avec le transfert entre un
"maitre" et son apprenti.
| noir sur blanc |
matière grise |
| peu de temps |
tout son temps |
| structuré |
cas par cas |
| pratiquement pas de retour |
feedback |
| information positive |
information négative |
Nous allons donc nous inspirer de ce processus pour développer notre système.
Dans un premier temps, l'"ingénieur de la connaissance" (bof) discute avec l'"expert".
Il construit un système initial. 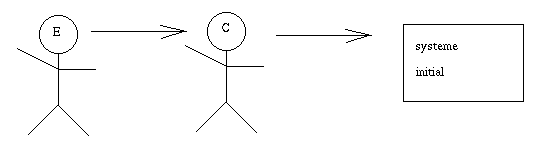
L'"expert" soumet un premier problème au système, et analyse la solution. 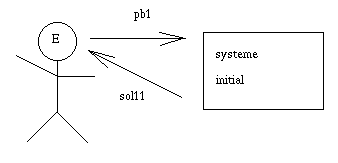
Le "cogniticien" (beurk) modifie le système : ajout de connaissances, suppression
de choses qui avaient été mal comprises.
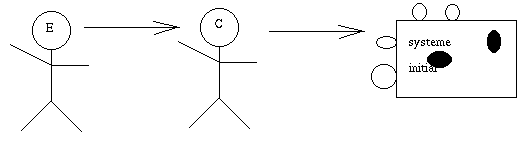
On recommence.
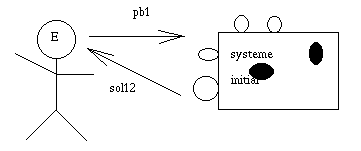
Même ce qui vient d'être ajouté est remis en question. 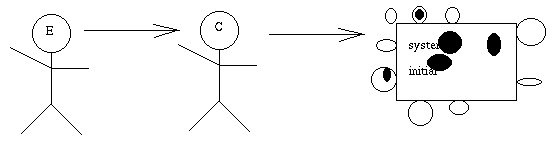
Et on continue ainsi jusqu'à ce que, en moyenne, la solution à n'importe quel
problème soit jugée acceptable.
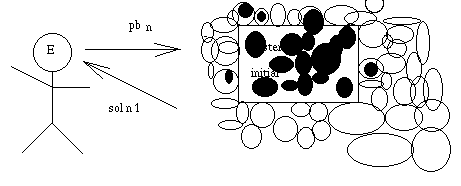
Le processus a convergé, on a capturé la connaissance.
Sauf que ce procédé est impraticable : une étude commandée en 1972 par le DoD
a montré que, s'il fallait $75 pour écrire une instruction, il en fallait 4000
pour modifier une instruction. Or ici, la quasi totalité du programme résulte
de modifications.
EXPLIQUER LA DIFFERENCE DE COÜT ENTRE ECRITURE
ET MODIFICATION D'UNE INSTRUCTION (EN MOYENNE); ILLUSTRER PAR UN EXEMPLE D'APPLICATION
(correction avec illustration)
1.4. Représentations déclaratives
Que faire? Rendre les
modifications moins couteuses. D'où vient le coût? Du fait que le programme est
structuré, donc que lorsqu'on veut modifier une instruction il faut prendre
toutes les autres en compte, et répercuter la modification en de nombreux
endroits. Ce qu'il faudrait, ce serait pouvoir exprimer les connaissances de
manière déclarative, c'est-à-dire indépendamment de leur mode d'emploi, pouvoir
dire le "quoi" sans se préoccuper du "comment".
Par analogie avec la
Thermodynamique, un programme classique a une faible entropie, alors qu'on en
veut une très grande ; au lieu d'un cristal, on voudrait un programme
"gazeux".
Il existe un langage qui permet cela, connu depuis 2400 ans, qui
s'appelle la Logique. C'est pour cette raison que nous allons étudier la
Logique, ou plus exactement les Logiques.