EXEMPLE DETAILLE

Regardons un exemple simple en détail :

Prenons une fonction simple f : x->x² à optimiser sur l'intervalle [0;31] , avec x entier.

1ère étape : Codage des données du problème

Chaque valeur de x peut être codée en base 2 sur 5 bits. Chacun de ces 5 bits correspond donc à un gène et les 5 bits ensemble seront le chromosome de x. Par exemple x=12 sera codé par le chromosome 01100.

Ici la fonction d'adaptation sera f.

2ème étape : Génération d'une population aléatoire

Dans cet exemple on se limite à une population de 4 individus.
Nous tirons aléatoirement les nombres (individus) 13, 24, 8 et 19.

3ème étape : Sélction et croisements (crossover)

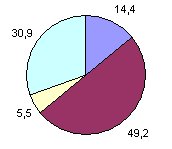
A l'aide de la dernière colonne du tableau 1 nous contruisons la roulette de croisement qui permet de selectionner les individus qui participeront à la reproduction, proportionnellement à leur adaptation.

	Figure 1 : Roulette de croisement

Cette roulette est lancée 4 fois afin de séléctionner les 4 individus qui participeront à la reproduction. Nous sélectionnons les individus numéros 1, 2, 2 et 4.

Pour chacun de ces individus on choisit un partenaire de manière aléatoire ainsi qu'on point de croisement des gènes.

Il ne reste alors plus qu'à effectuer les croisements en question en échangeant les parties gauche et droite des chromosomes de chaques partenaires.

Le résultat de cette étape est résumé dans le tableau suivant :

Nous observons :

• Total d'adaptation : 1754
• Moyenne d'adaptation : 439
• Maximum d'adaptation : 729

La population après une génération est globalement plus adaptée que ses géniteurs avec quelques individus très forts (625 et 729 d'adaptation).

4ème étape : On recommence avec la génération obtenue, et ce jusqu'à ce qu'on atteigne une condition fixée par l'utilisateur (nombre maximum de générations, adaptation satisfaisante,...).

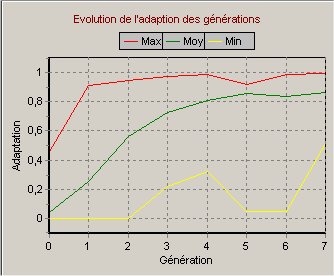
Voici un graphique des résultats obtenus sur 7 générations, avec un population de 50 individus :

	Figure 2 : Evolution de l'adaptation des générations. On a pris la fonction d'adaption F(x)=f(x)/31² afin de normaliser les résultats sur [0;1]

Raffinements de la méthode :

1. Lors de l'étape de croisement on peut décider si les partenaires se croiseront effectivement ou pas en introduisant une probabilité de croisement (en général comprise entre 0.6 et 0.8).
2. Afin de diversifier le patrimoine génétique de notre population on introduit des mutations de gènes : A chaque croisement on décide de manière aléatoire, pour chaque gène, s'il va être inversé. La probabilité de mutation est fixée par l'utilisateur (faible, de l'ordre de 0.01 mais variable selon les problèmes). Cela permet d'éviter une stagnation de la population vers un état "moyen".