Échantillonnage basse discrépance et bruit bleu en informatique graphique














David Coeurjolly









                 

Contexte

Synthèse d'image : simulation transport lumineux

[Kaj86] $$\mathcal{I}(\vx) = L_e(\vx) + \int_\mathcal{H} \rho(\vp, \vx) \mathcal{I}(\vp) d\vp$$

Approximation numérique

Estimateurs de Monte-Carlo

$$\int_D f(x)dx \approx \frac{1}{n} \sum_{i=0}^{n} f(x_i)$$

Estimateurs de Monte-Carlo

$$\int_D f(x)dx \approx \frac{1}{n} \sum_{i=0}^{n} f(x_i)$$

Estimateurs de Monte-Carlo

$$\int_D f(x)dx \approx \frac{1}{n} \sum_{i=0}^{n} f(x_i)$$

Echantillonnage n-D

De nombreuses stratégies

  • de construction de chemins (bidirectionnelle, gradient domain...)
  • d'échantillonnage (adaptatives, importance sampling, multiple importance sampling...)
  • de corrélation de l'échantillonnage d'un pixel à un autre
  • de post-filtrage/reconstruction...
  • ...

Besoin de processus ponctuels efficaces

Erreur, Biais, Variance

$\mathcal{I} = \int_\Omega fdx$

$\mathcal{I}_n = \frac{1}{n}\sum f(x_i), \quad \{x_i\}\in \Omega$

$$ \Delta := | \mathcal{I} -\mathcal{I}_n | $$

$$ \langle \Delta\rangle := \mathcal{I} - \langle \mathcal{I}_n \rangle $$

$$ \text{Var}(\mathcal{I}_n) := \langle \mathcal{I}_n^2 \rangle - \langle \mathcal{I}_n \rangle^2 $$

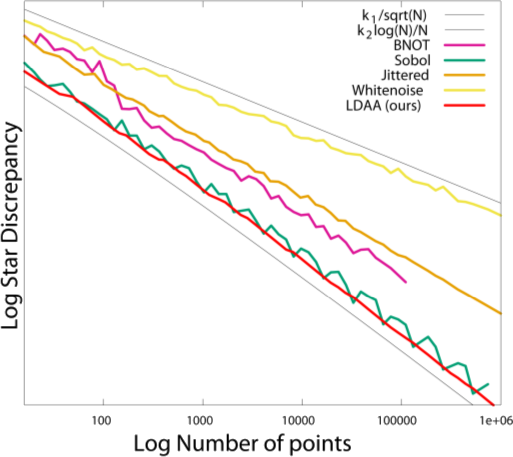
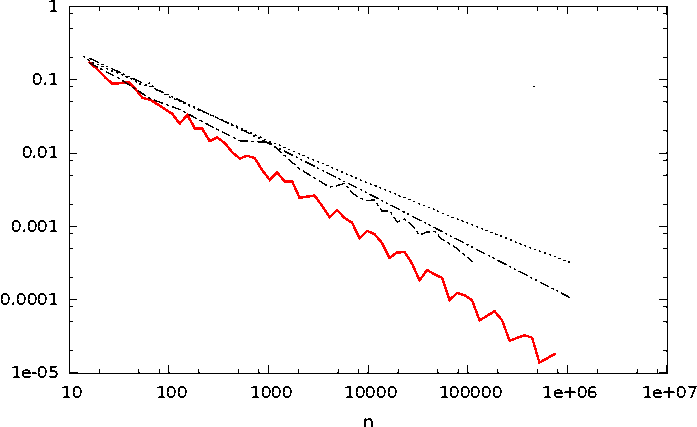
Vitesse de convergence

Quatres grandes familles


[Shi91]
(Processus de Poisson, Poisson stratifié,...)

[Hal64]                 [HH64]                 [Sob67]
(Hammersley, Halton, Sobol,...)

[Coo96]                 [Bri07]                 [MF92]
(Tirage uniforme da, Halton, Sobol,...)

[GBO+12]              [CYK+12]                [Fat11]
(Formulation énergétique, )

Quelques vitesses de convergence

$n$ échantillons dans $[0,1)^d$

$$ Var(I_n) = O\left(\frac{\sigma_f^2}{{n}}\right) $$

$$ \Delta = O\left(\frac{ \log(n)^{d-1}}{n}\right) $$

$$ Var(I_n) = O\left(\frac{1}{n\sqrt[d]{n}} \right) $$

Aliasing et corrélation

Aliasing et corrélation

Aliasing et corrélation

Bilan

Processus ponctuels :

  • Uniformes dans $[0,1)^d$
  • Borne asypmtotique sur l'erreur ou la variance de l'estimateur de MC / QMC
  • Très souvent corrélation dans la position des échantillons

Contexte rendu d'images :

  • Plutôt faible nombre de dimensions (~30/40)
  • Peu de structures (aliasing)
  • Faible erreur à peu d'échantillons
  • Echantillonneur rapide et progressif

Outils d'évaluation

Discrépance

Mesure d'uniformité d'une distribution de points $P_n$

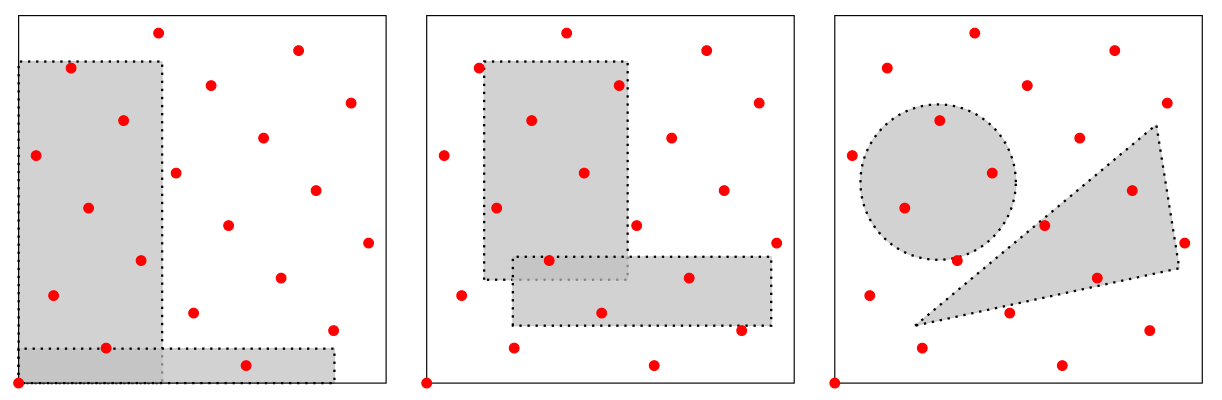
Star
discrepancy		 Extreme discrepancy Isotropic discrepancy
$\mathcal{D}_*(P_n) := \sup_{\vv \in [0, 1)^d} \left| v_1 \cdots v_d - \alpha( P_n, \vv ) \right| $
$$ \Delta \leq \mathcal{D}_*(P_n)V(f) $$

$f$ à variation bornée au sens de Hardy & Krause

Discrépance

Un échantillonneur est dit basse discrépance si sa discrépance décroit en $O\left(\frac{\log(n)^{d-1}}{n}\right)$.

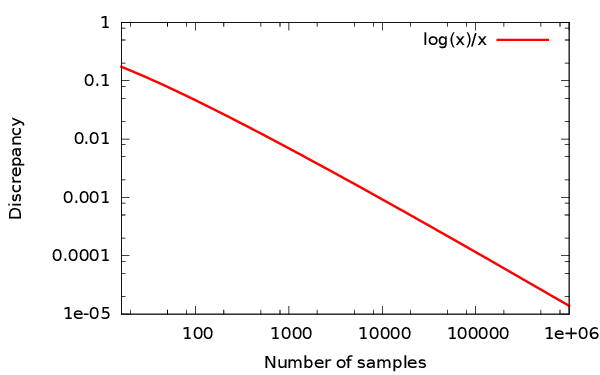
$$ \Delta = O\left(\frac{ \log(n)^{d-1}}{n}\right) $$

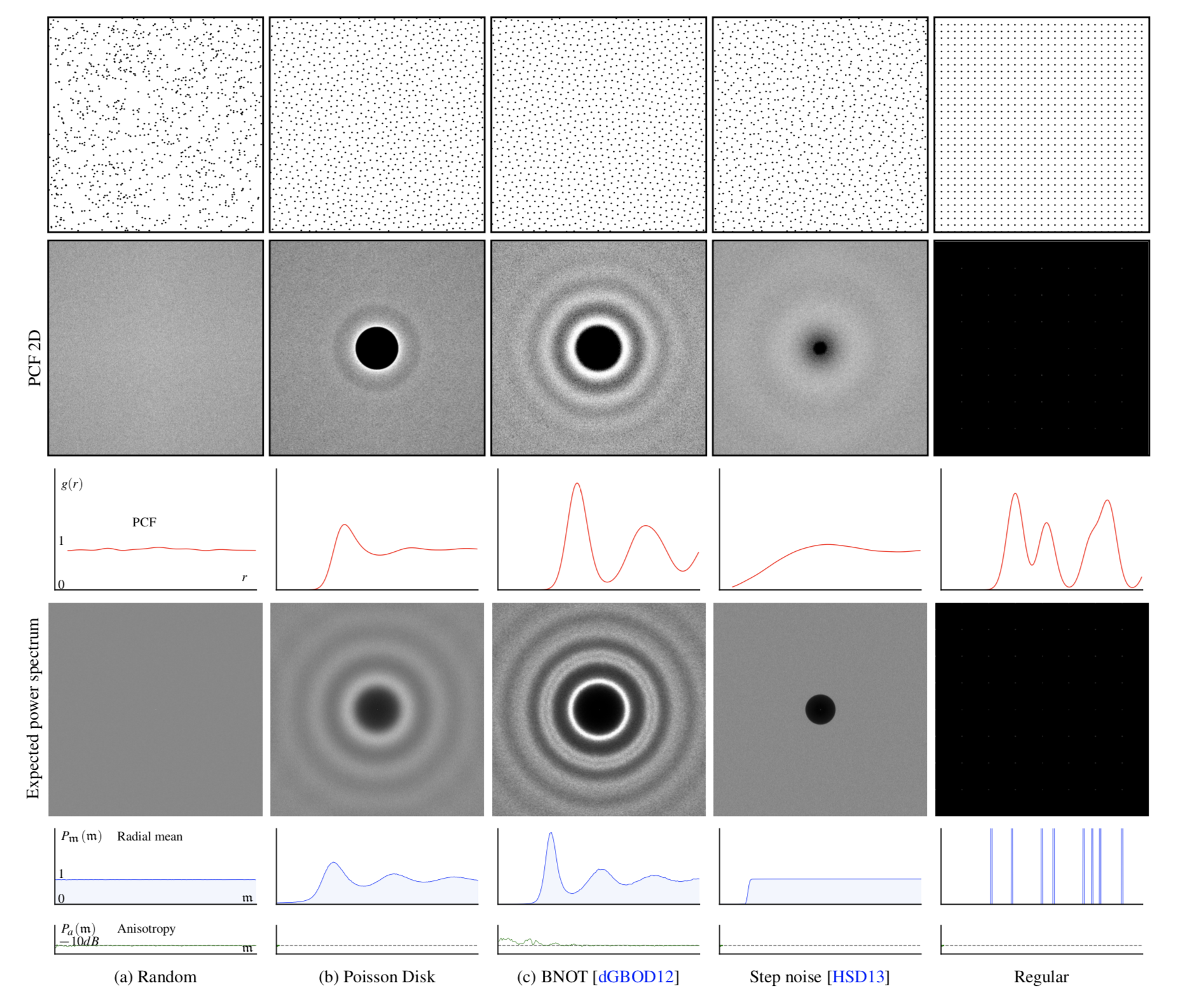
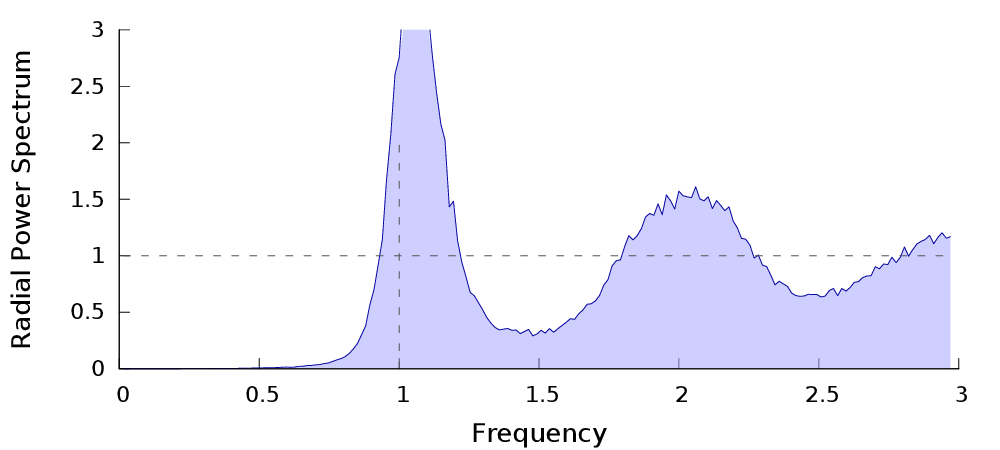
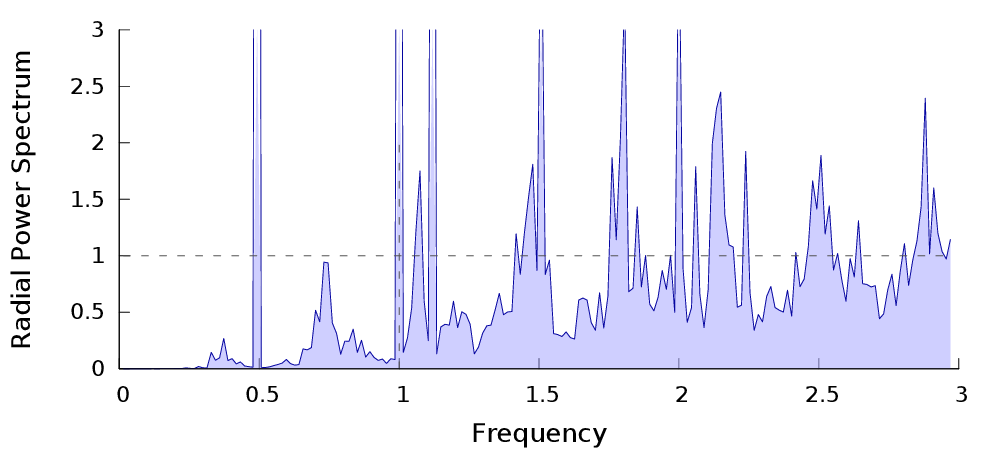
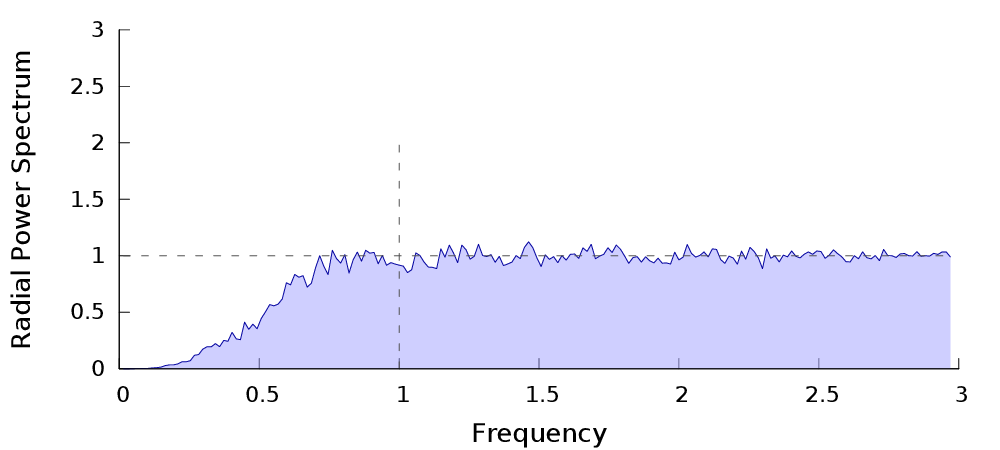
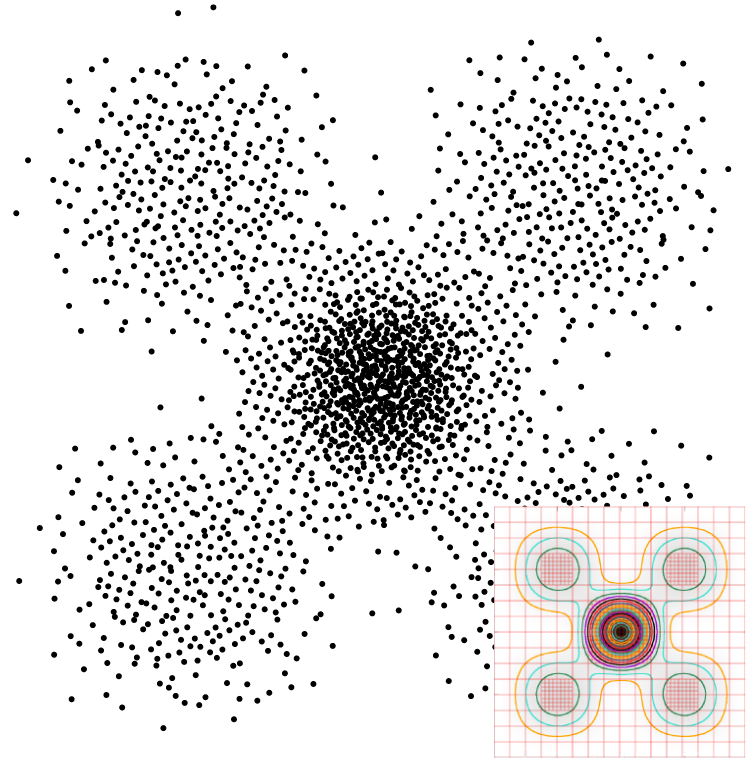
Caractéristiques fréquentielles

$P_n$ Spectre de puissance Radial

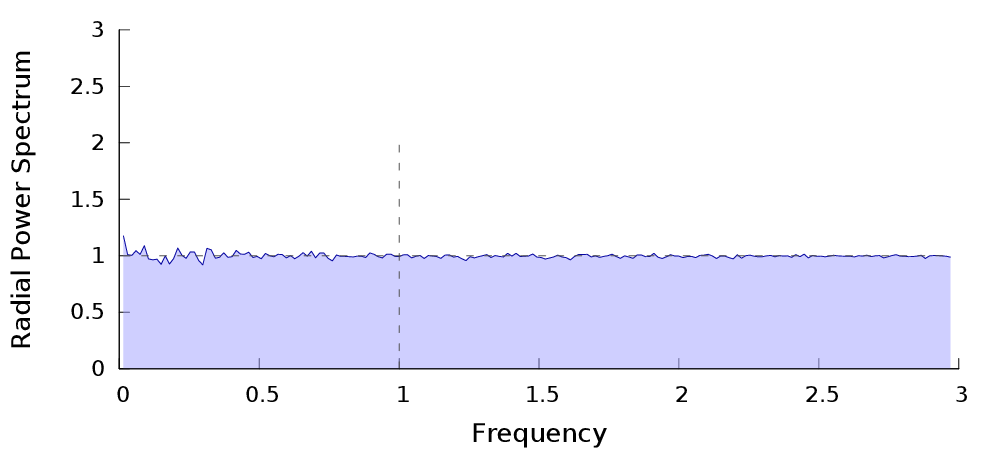
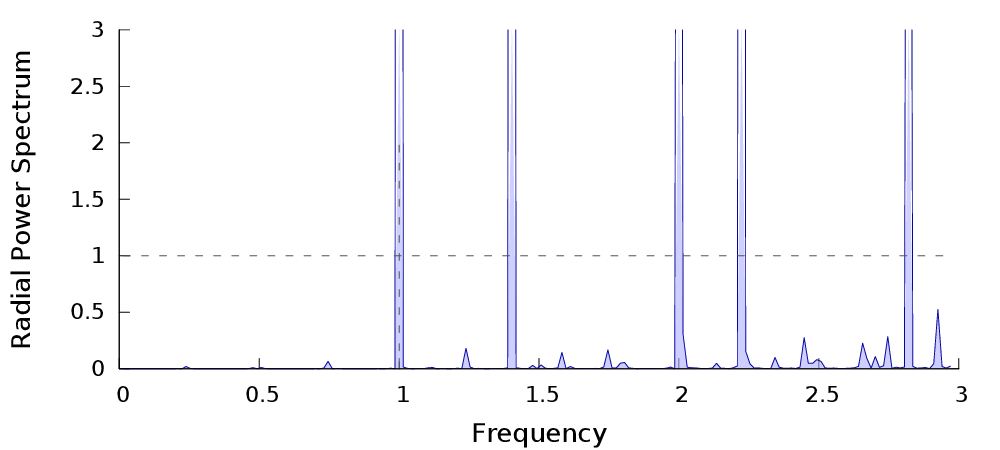
Caractéristiques fréquentielles

Les pics fréquentiels provoquent des artefacts visuels.
$sin(x^2 + y^2)$

Analyse

$$S(x) = \frac{1}{n}\sum_{k=1}^n \alpha_k \delta(x-x_k)\quad \text{et son $m$-ième coefficient de Fourier}\quad \mathbf{S}_m = \frac{1}{n}\sum_{k=1}^n \alpha_k e^{-i2\pi m x_k}\,,$$ nous avons $$\mathcal{I}_n=\int_0^1 f(x)S(x)dx = \int_\mathbb{R} \mathcal{F}_f(v)\mathcal{F}_S(v)dv =\sum_{m=-\infty}^{\infty} \mathbf{f}_m^* \mathbf{S}_m$$

Si $S(x)$ est une réalisation d'un processus ponctuel :

$$\langle \Delta \rangle = \mathbf{f}_{0}^*(1 - \langle \mathbf{S}_0\rangle) - \sum_{m\in\mathbb{Z}, m\neq 0} \mathbf{f}_m^*\langle \mathbf{S}_m\rangle$$ $$Var({I}_n) = \mathbf{f}_0^*\mathbf{f}_0 Var(\mathbf{S}_0) + \sum_{m\in\mathbb{Z}, m\neq 0}\mathbf{f}_m^*\mathbf{f}_m\langle \mathbf{S}_m^*\mathbf{S}_m\rangle + \sum_{m \in \mathbb{Z}}\sum_{l \in \mathbb{Z}, l\neq m} \mathbf{f}_m^*\mathbf{f}_l\langle \mathbf{S}_m^*\mathbf{S}_l\rangle$$

$\langle \Delta \rangle = \mathbf{f}_{0}^* - \sum_{m\in\mathbb{Z}, m\neq 0} \mathbf{f}_m^*\langle \mathbf{S}_m\rangle$
$\langle \Delta \rangle = 0$ si processus de Poisson ou non biaisé

$Var({I}_n) =\sum_{m\in\mathbb{Z}}\mathbf{f}_m^*\mathbf{f}_m\langle \mathbf{S}_m^*\mathbf{S}_m\rangle$

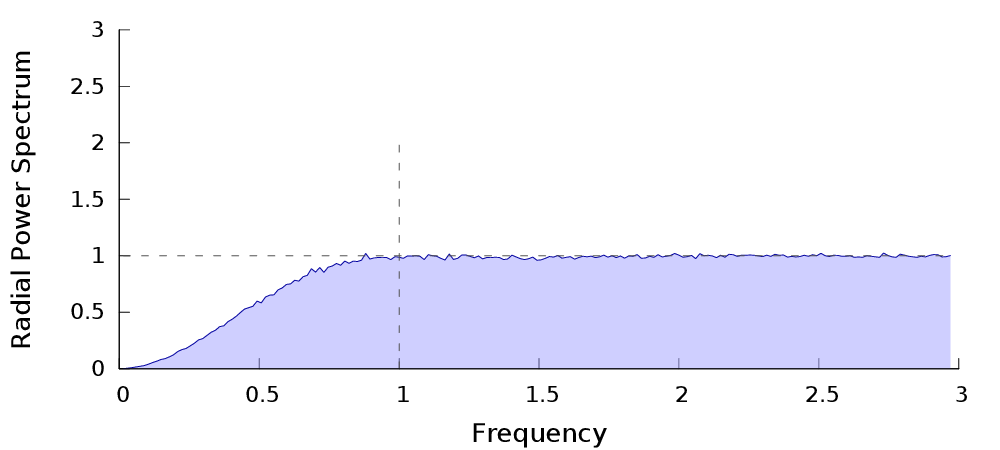
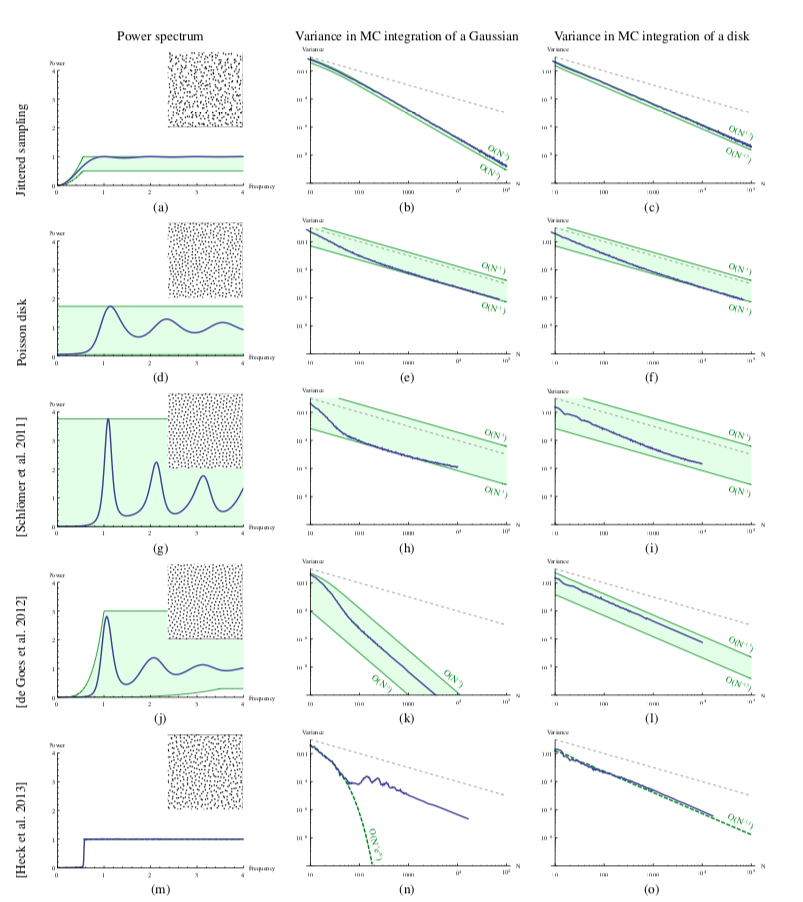
Caractéristiques fréquentielles

$Var({I}_n) =\sum_{m\in\mathbb{Z}}\mathbf{f}_m^*\mathbf{f}_m\langle \mathbf{S}_m^*\mathbf{S}_m\rangle$

Caractéristiques fréquentielles

$Var({I}_n) =\sum_{m\in\mathbb{Z}}\mathbf{f}_m^*\mathbf{f}_m\langle \mathbf{S}_m^*\mathbf{S}_m\rangle$

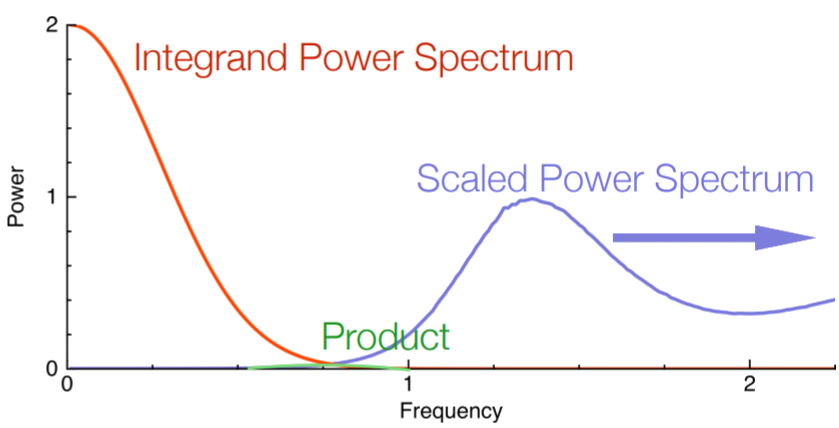
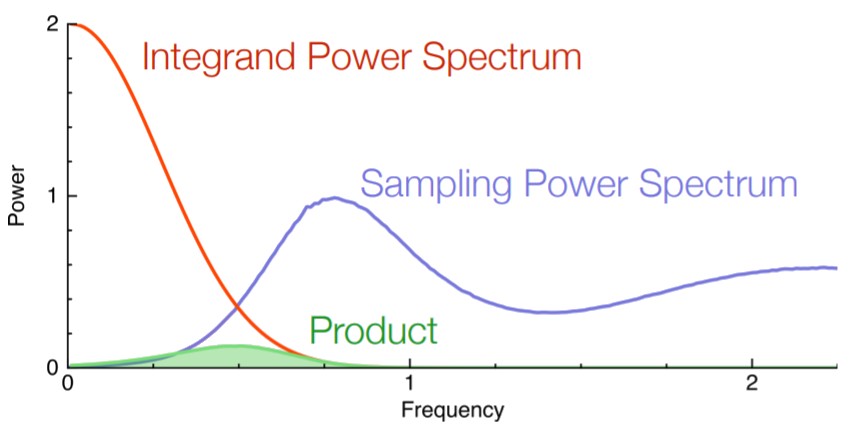
Contrôler la réduction de variance = contrôler les fréquences basses du processus ponctuel






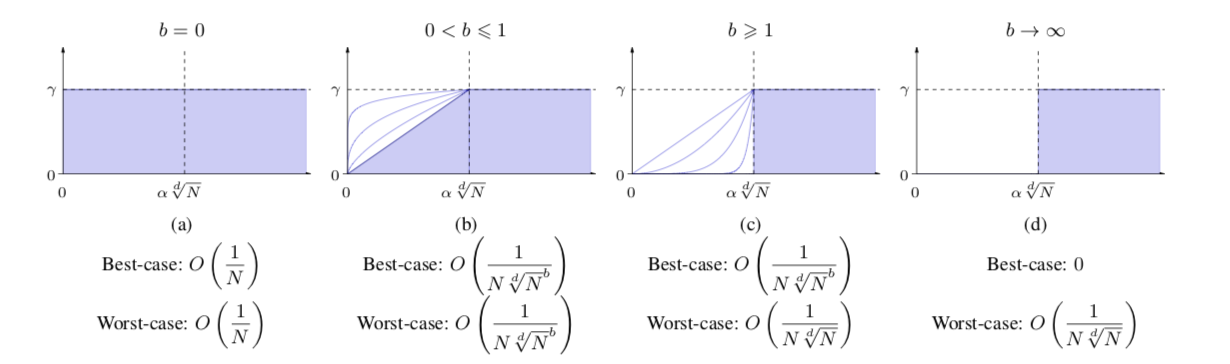
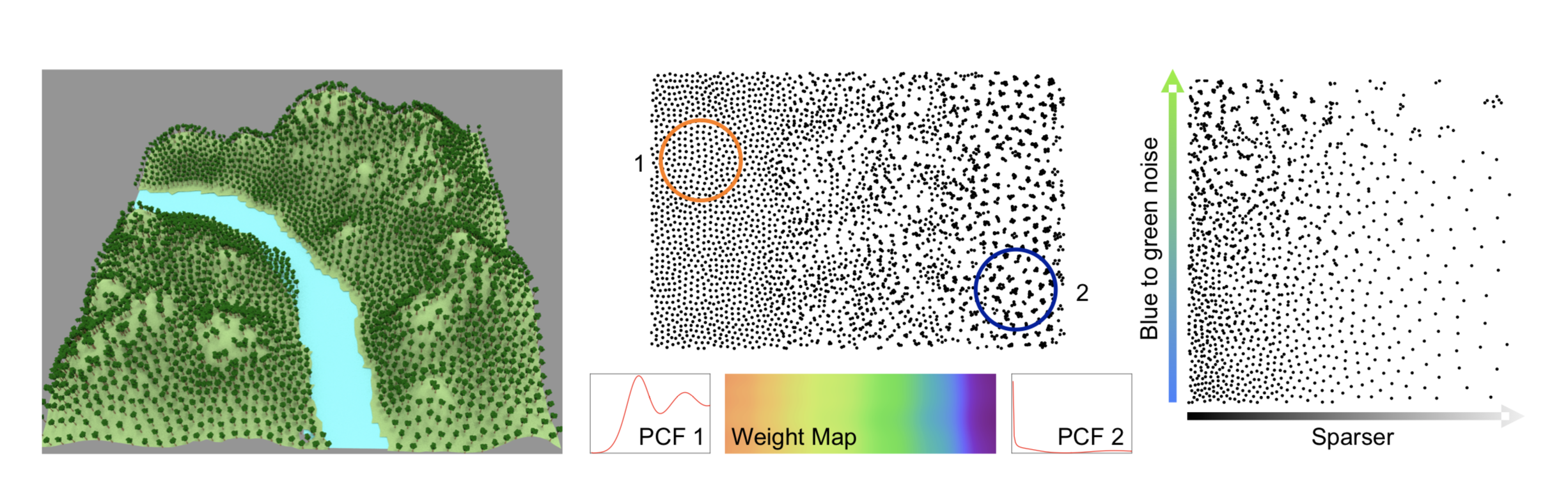
Caractéristiques spatiales





Processus ponctuels stochastiques (Pair Correlation Function, Analyse différentielle, ...)

Ce que l'on cherche

Processus ponctuels :

  • Uniformes dans $[0,1)^d$
  • Borne asypmtotique sur l'erreur ou la variance de l'estimateur de MC / QMC

Contexte rendu d'images :

  • Plutôt faible dimension de l'estimateur (~30/40)
  • Peu de structures (aliasing) et donc corrélation des échantillons
  • Faible erreur à peu d'échantillons
  • Echantillonneur rapide et progressif
LDS + BN

Polyhex





[WPC+14] Florent Wachtel, Adrien Pilleboue, David Coeurjolly, Katherine Breeden, Gurprit Singh, Gaël Cathelin, Fernando de Goes, Mathieu Desbrun, Victor Ostromoukhov. Fast Tile-Based Adaptive Sampling with User-Specified Fourier Spectra. ACM Transactions on Graphics (Proceedings of SIGGRAPH), 33(4):56:1-56:11, August 2014.

Système de pavage apériodique avec précalculs

  • Très grande vitesse de génération d'échantillons bruit bleu (+ 1 million de points par seconde)
  • Contrôle local de densité

...mais...

  • Uniquement 2D
  • Tables pré-calculées de grande dimension

  • 2D
  • Très rapide
  • Distribution bruit bleu quasi-parfaite
  • Pour des densités non-uniformes



  • 2D uniquement
  • Système de tuiles nécessitant une très grande table annexe

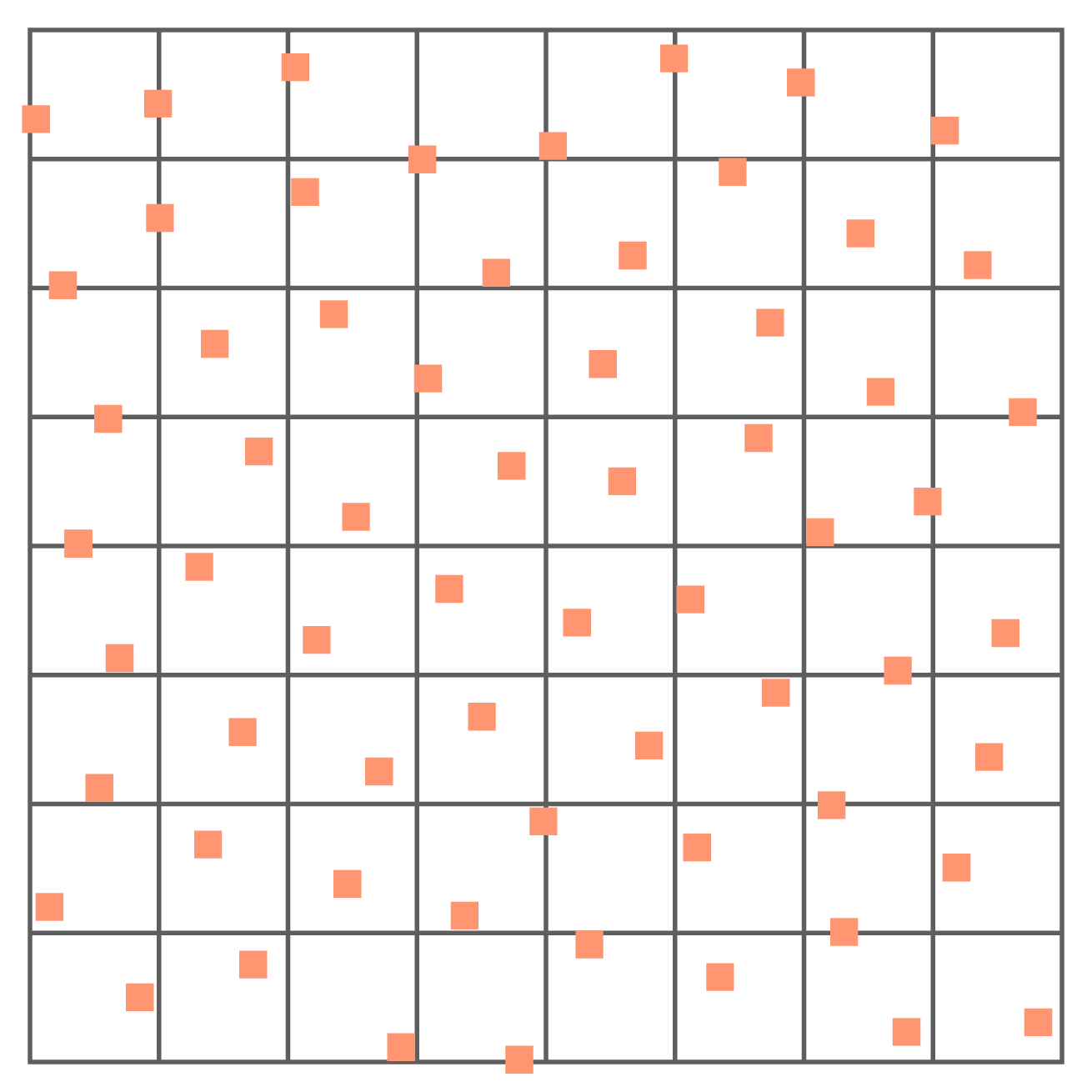
Low Discrepancy Blue Noise

Bruit bleu basse discrépance 2-D

      
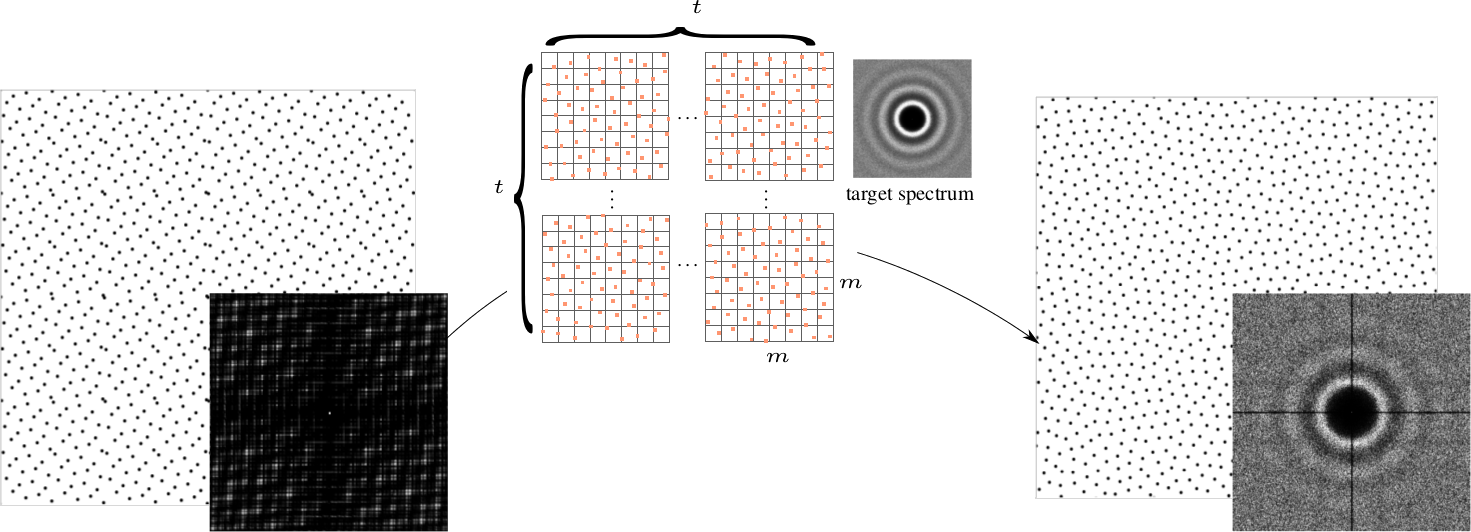
[APC+16] Ahmed A., Perrier H., Coeurjolly D., Ostromoukhov V., Guo J., Dongming Y., Hui H., Deussen O.. Low discrepancy blue noise sampling. ACM Transactions on Graphics (Proceedings of ACM SIGGRAPH Asia 2016), 2016.

Notre méthode

Notre méthode

Notre méthode

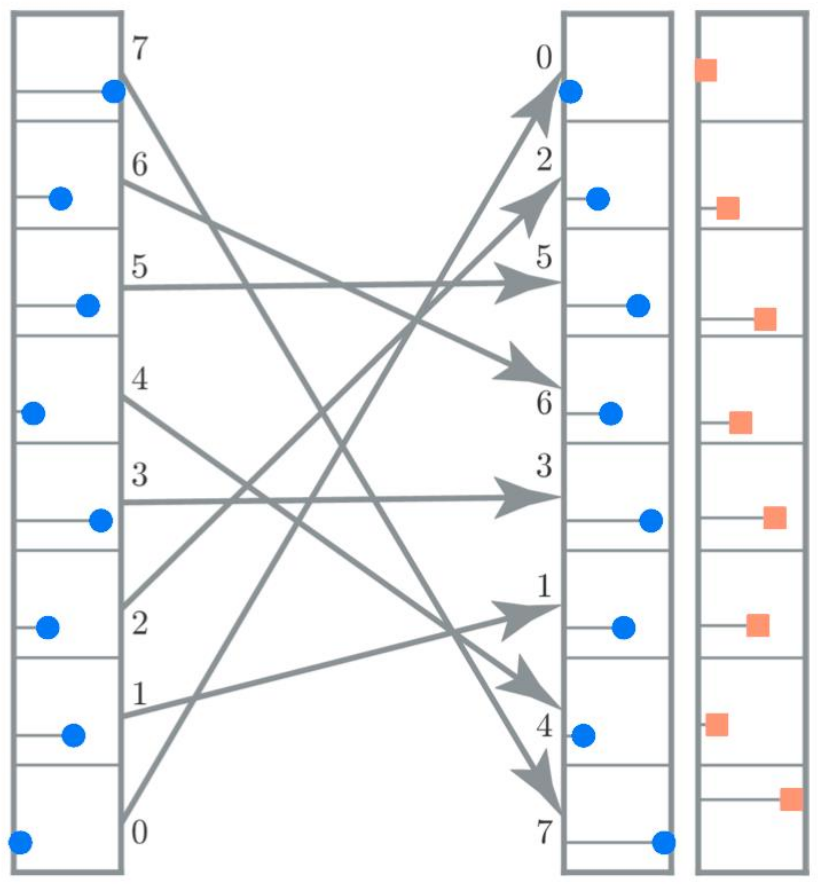
On calcule les permutations de taille $m$ à partir d'un ensemble de taille $t^2$. On les stocke ensuite dans une LUT pour générer des ensemble de taille $n$.

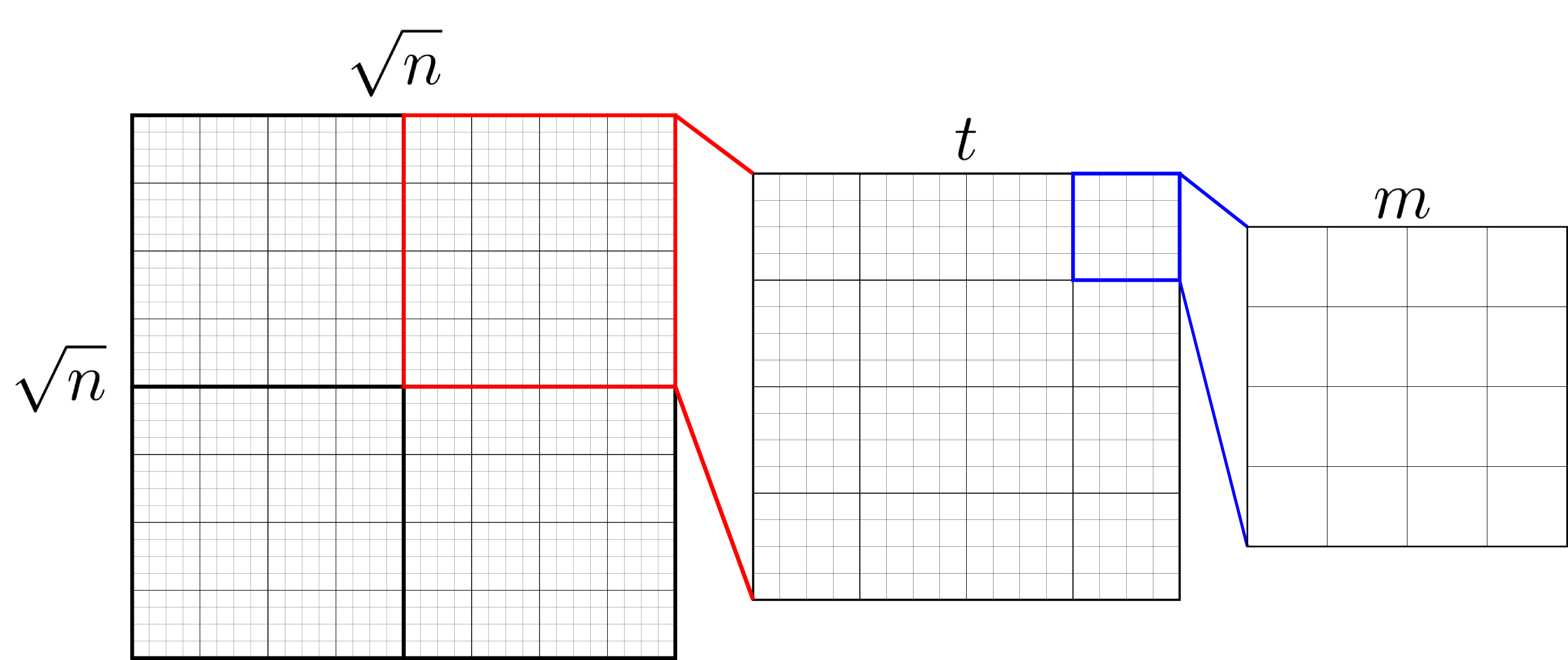
$$ \lbrace X + \phi(Y - Y\%m + L_X), \\ Y + \phi(X - X\%m + L_Y) \rbrace $$

Notre méthode

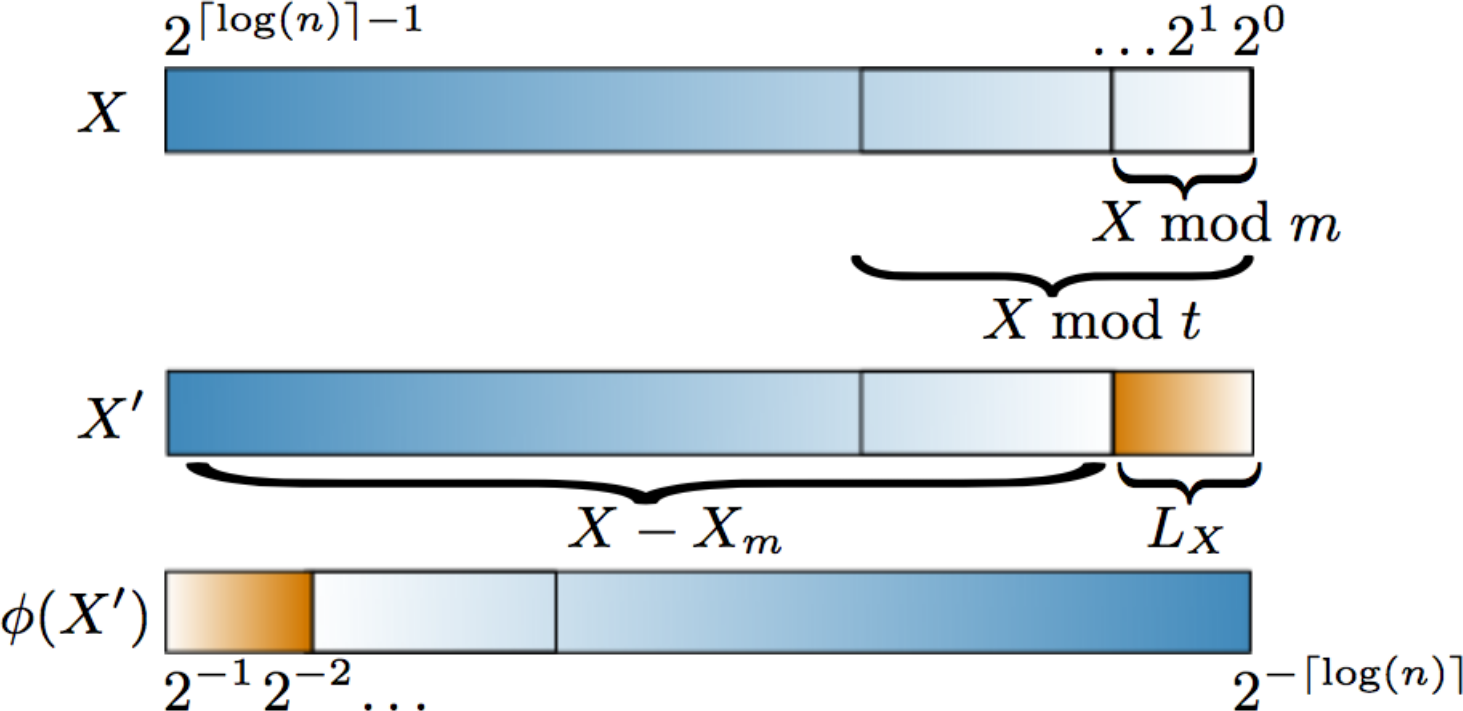
$$ \lbrace X + \phi(Y - Y\%m + L_X), \\ Y + \phi(X - X\%m + L_Y) \rbrace $$
Si $t$ est trop petit p/r à $n$, les permutations vont se répéter et les caractéristiques fréquentielles de l'ensemble de point vont se dégrader. Si $m$ est trop petit p/r à $t$, le spectre sera mal préservé.

Notre méthode

Résultats

BNOT [GBO+12] Sobol [Sob67]
Owen's Scrambling [Owe95] LDBN ($m=16$, $t=128$)

Résultats

BNOT [GBO+12] LDBN ($m=16$, $t=128$)
Step [HSD13] LDBN ($m=16$, $t=128$)

Résultats

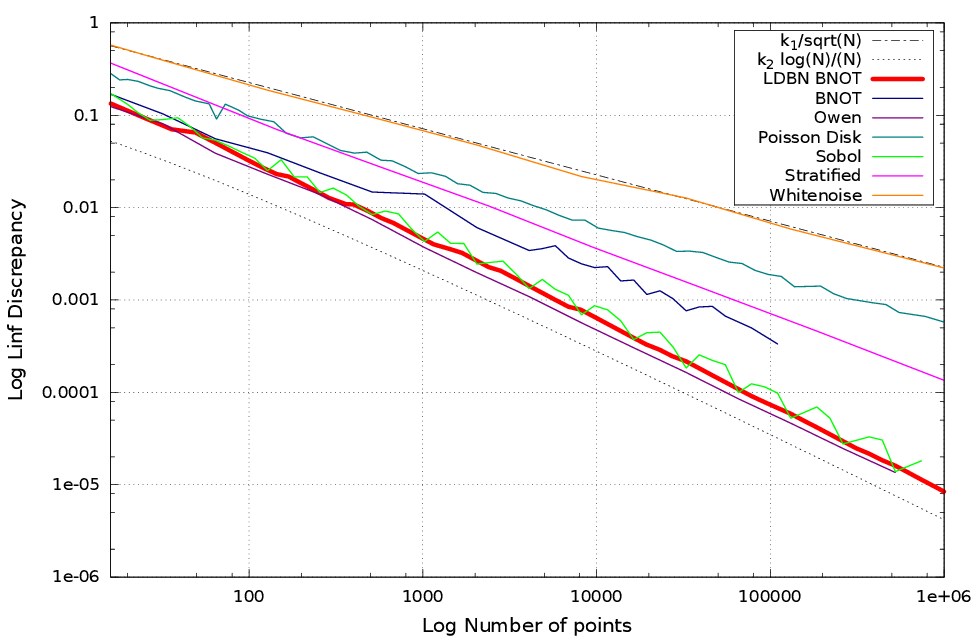
Résultats

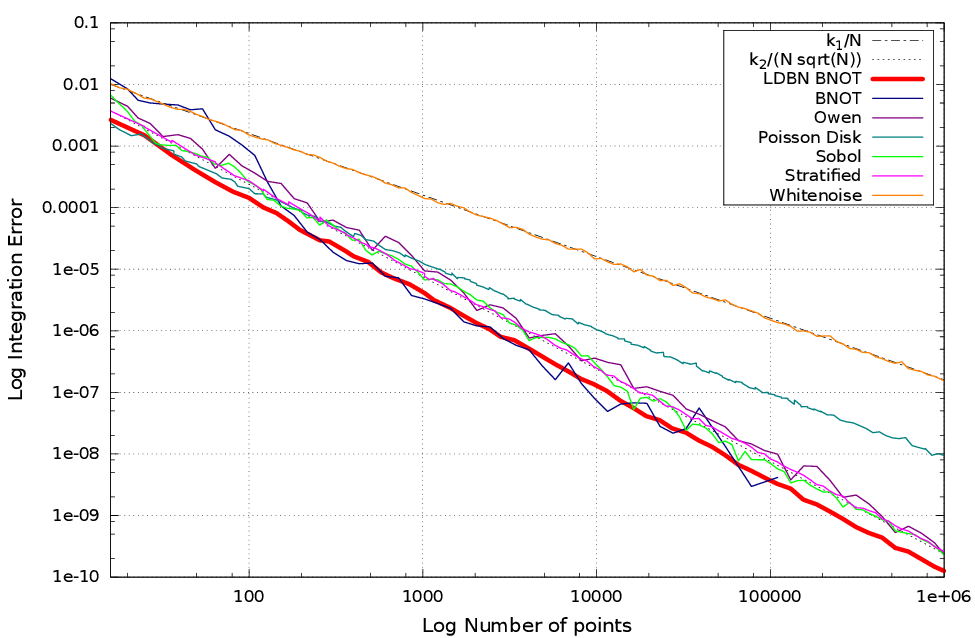
Résultats

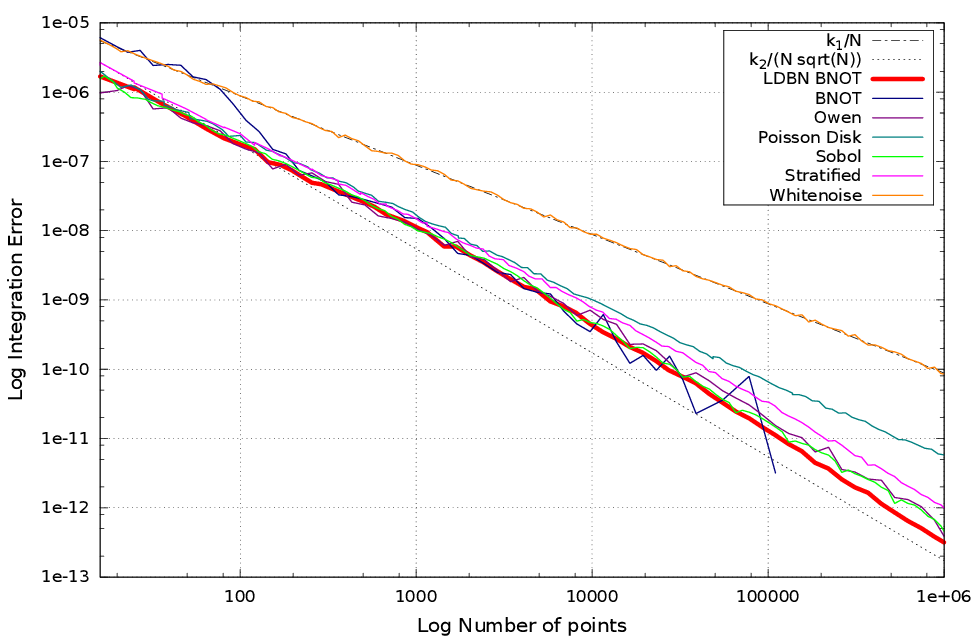
Résultats

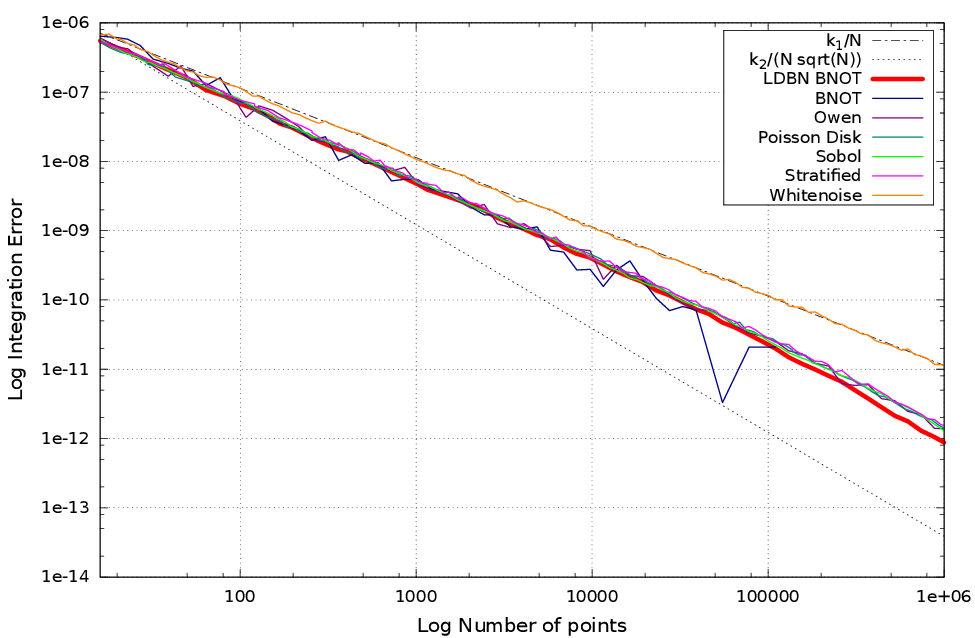
Résultats

BNOT [GBO+12] Sobol [Sob67] Owen's Scrambling [Owe95] LDBN ($m=16$, $t=128$)

  • 2D
  • Très rapide
  • Très bonne distribution bruit bleu
  • Propriétés de basse discrépance



  • 2D uniquement
  • Notion d'ensemble basse-discrépance mais pas de séquence

Sequences with Low-Discrepancy Blue-Noise 2-D Projections

Principe

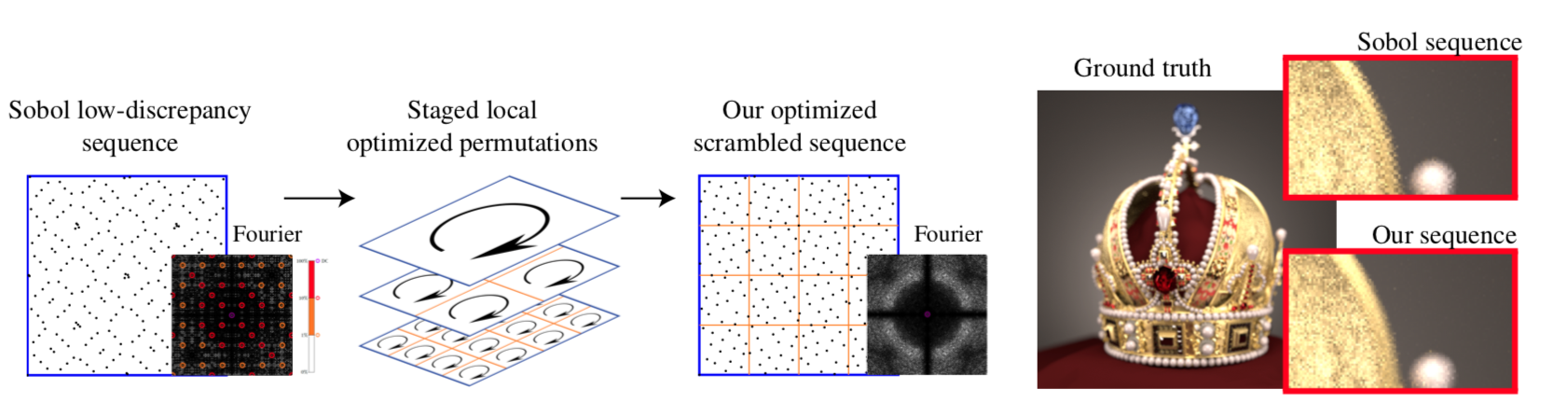
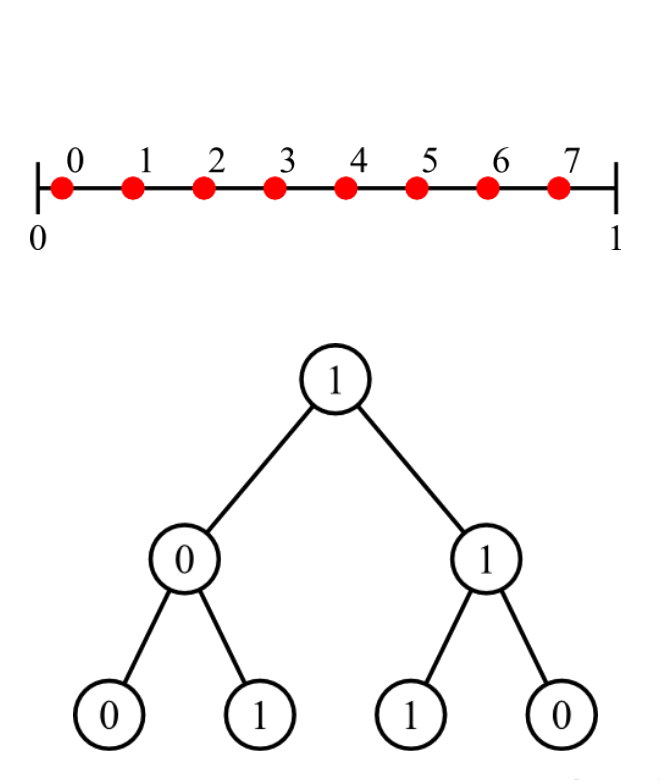
[PC+18] Hélène Perrier, David Coeurjolly, Feng Xie, Matt Pharr, Pat Hanrahan, Victor Ostromoukhov. Sequences with Low-Discrepancy Blue-Noise 2-D Projections. Computer Graphics Forum (Proceedings of Eurographics), 37(2), 2018.

Owen's scrambling [Owe95]

Owen's scrambling [Owe95]

Owen's scrambling [Owe95]

Owen's scrambling [Owe95]

Owen's scrambling [Owe95]

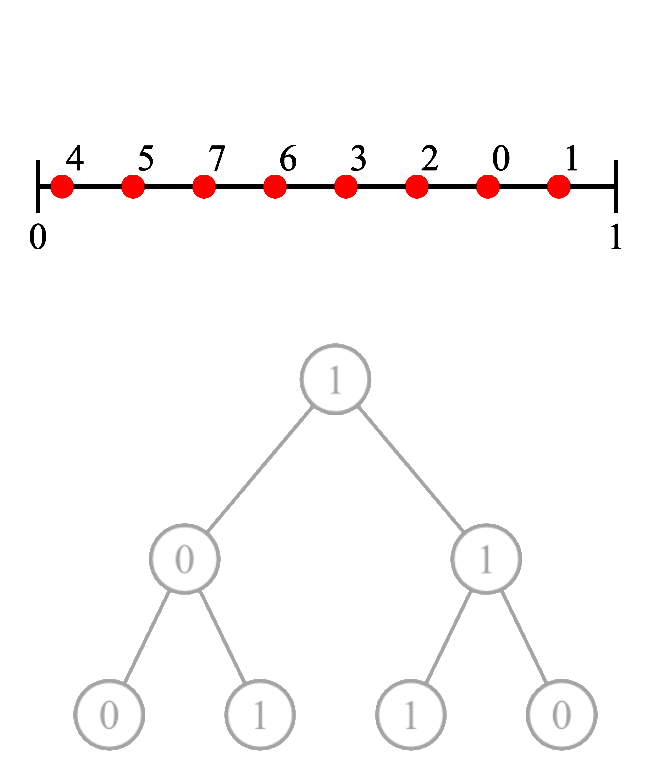
Owen's scrambling [Owe95]







Niveau 1, 2-D, $K=4$

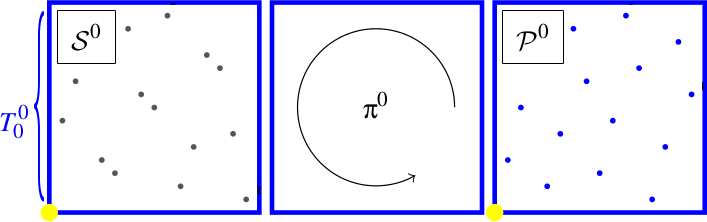
On génère $K^d=16$ points à partir de Sobol. On note cet ensemble $\mathcal{S_0}$.

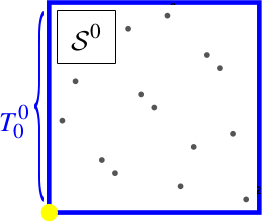
Et on les mélange en utilisant un Owen scrambling pour leur donner un spectre bruit bleu. On note le nouvel ensemble $\mathcal{P_0}$.

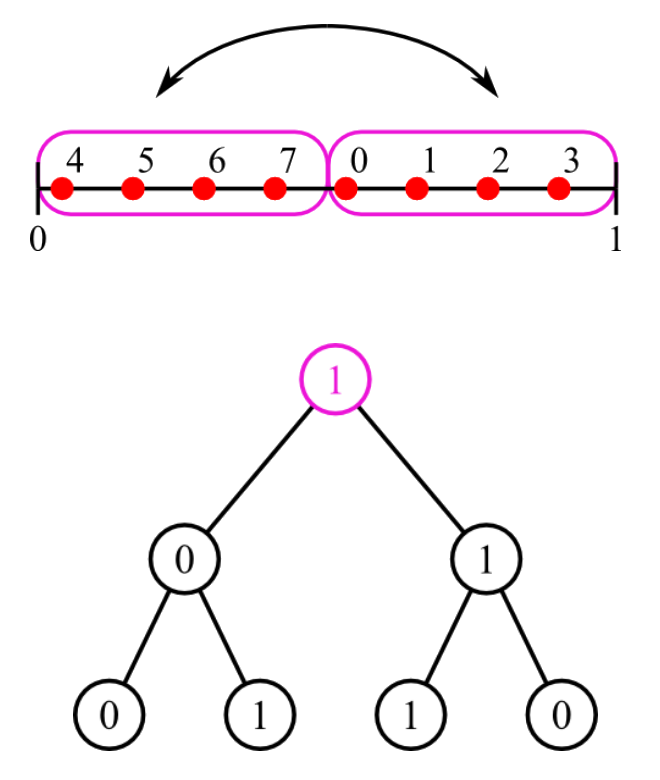
Niveau 2, 2-D, $K=4$

On génère $K^{2d}=256$ points à partir de Sobol. On note cet ensemble $\mathcal{S_1}$.

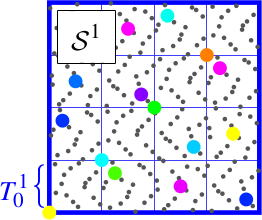
On commence par appliquer un scrambling global sur cet ensemble pour reconstruire $\mathcal{P_0}$. On note le nouvel ensemble $\mathcal{Q_1}$.

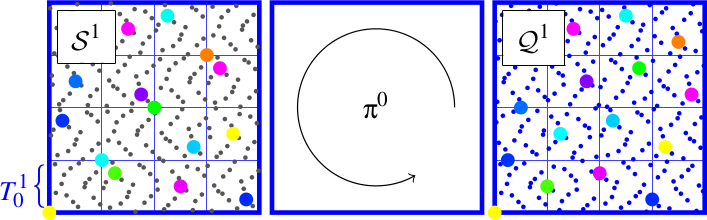
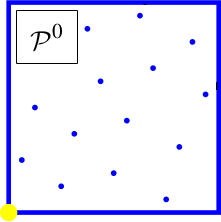
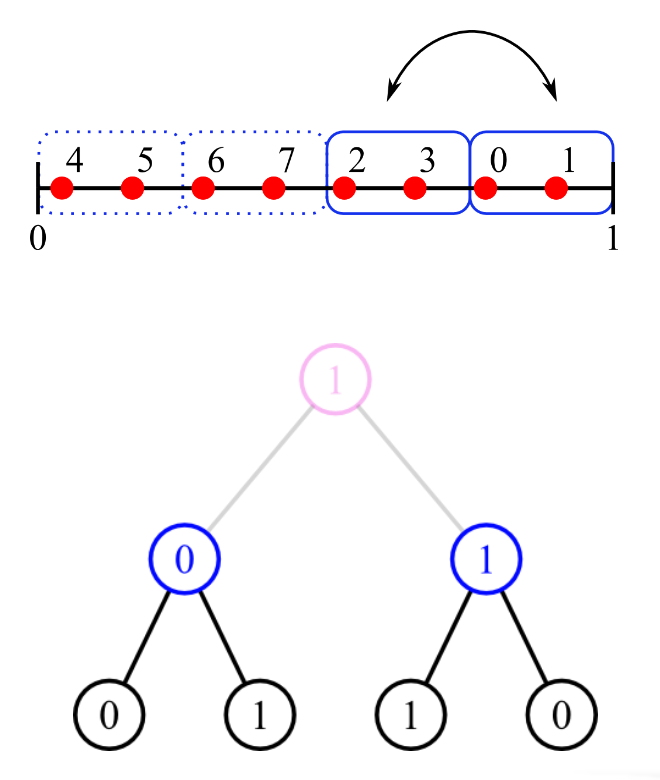
Niveau 2, 2-D, $K=4$

Ensuite, on scramble les points dans chaque tuile $\mathcal{T_1^{i}}$ de $\mathcal{Q_1}$ pour obtenir un spectre globalement bruit bleu.

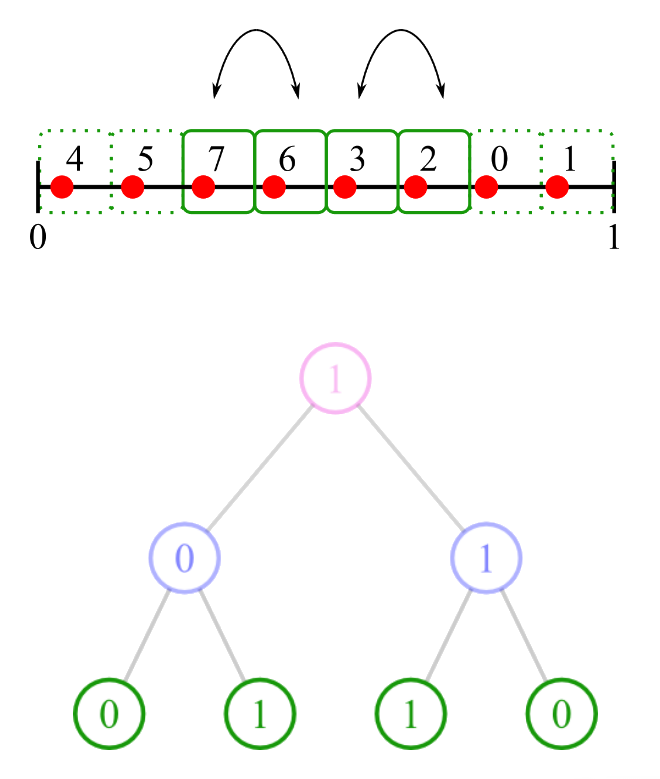
Et ainsi de suite ...

Garanties

Quand $d = 2$, si $\mathcal{Q}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$, $\mathcal{P}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$

Si l'ensemble initial est dyadique en base $K$ (et donc est basse discrépance), notre ensemble de permutations locales préserve la dyadicité de cet ensemble (et donc la basse discrépance).

Garanties

Quand $d = 2$, si $\mathcal{Q}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$, $\mathcal{P}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$

Si l'ensemble initial est dyadique en base $K$ (et donc est basse discrépance), notre ensemble de permutations locales préserve la dyadicité de cet ensemble (et donc la basse discrépance).

Quand $d = 2$, si $\mathcal{S}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$, $\mathcal{Q}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$

Si l'ensemble initial est dyadique en base $K$ (et donc est basse discrépance), notre permutation globale préserve la dyadicité de cet ensemble (et donc la basse discrépance).

Garanties

Quand $d = 2$, si $\mathcal{S}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$, $\mathcal{P}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$

Si l'ensemble initial est dyadique en base $K$ (et donc est basse discrépance), notre permutation préserve la dyadicité de l'ensemble (et donc la basse discrépance).

Pipeline final

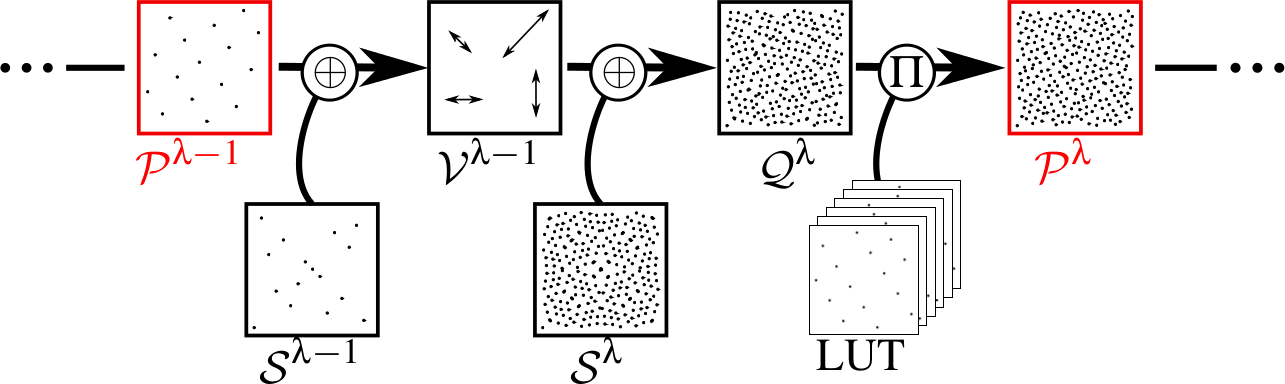
n-D

n-D obtenu par scrambling indépendant de projections 2D.

Adaptatif

Résultats

BNOT [GBO+12] Owen's Scrambling [Owe95]
LDBN MultiProj

Résultats

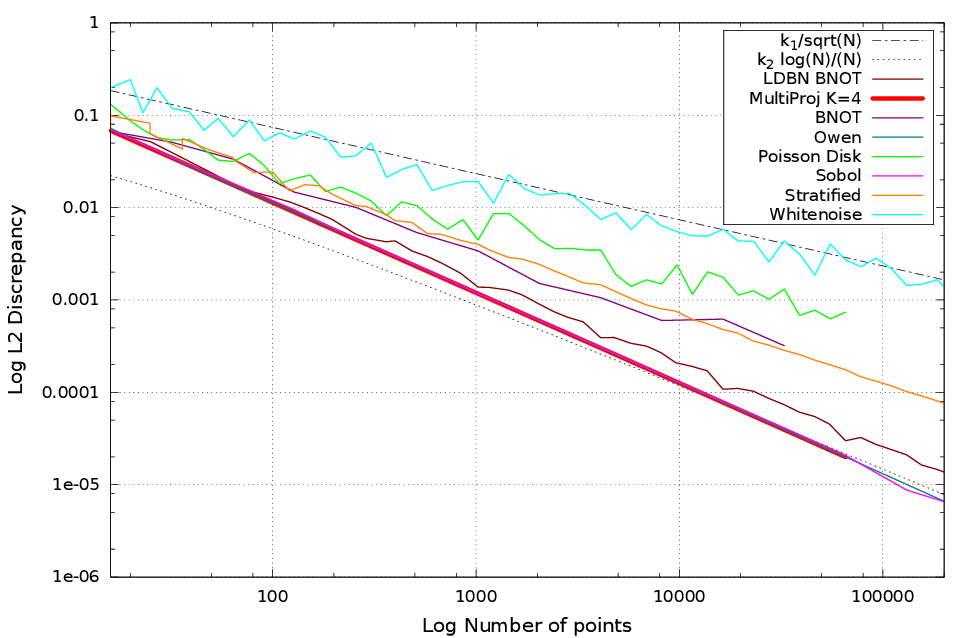
Résultats

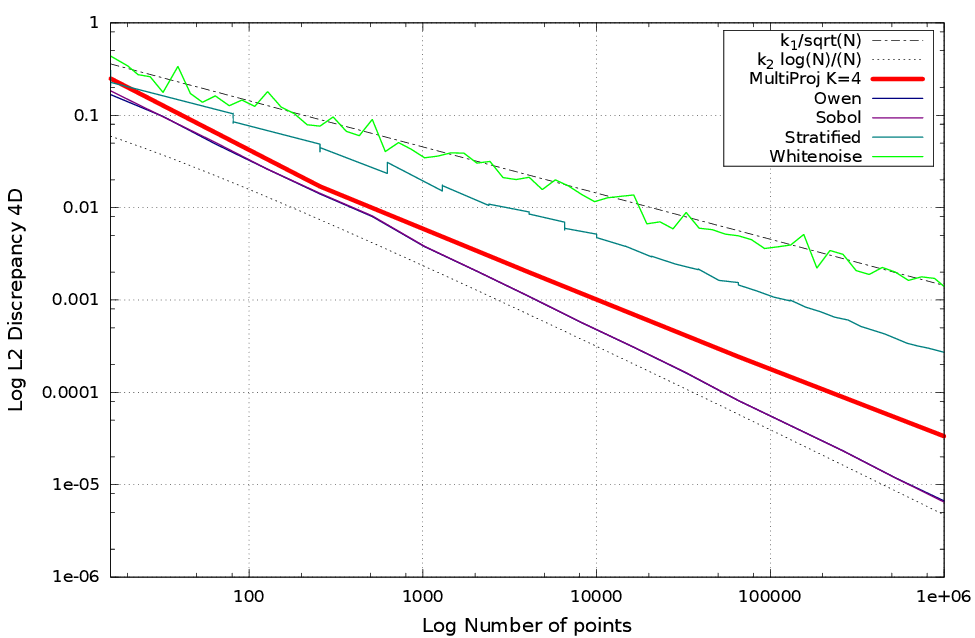
Résultats

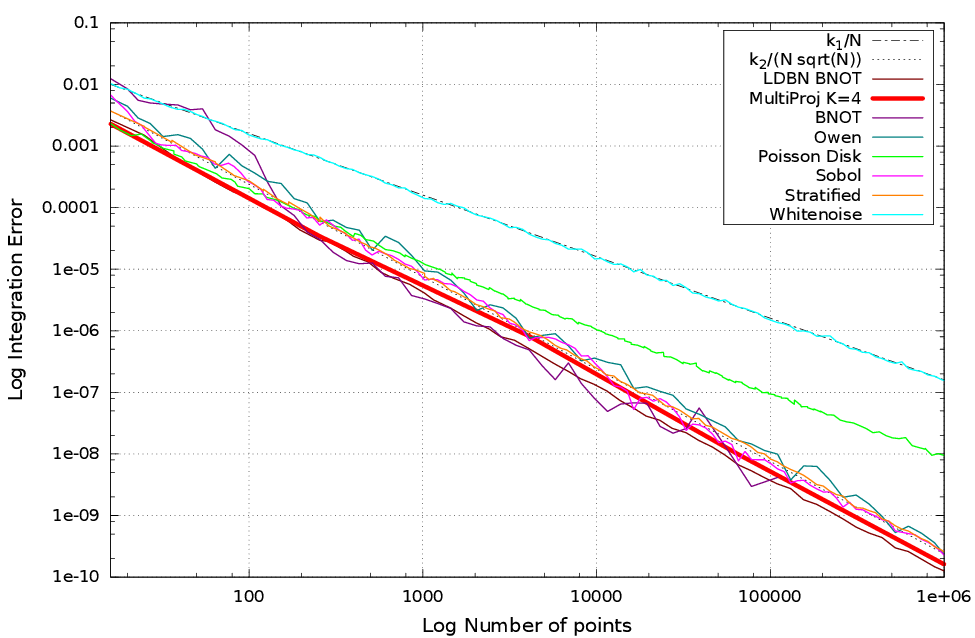
Résultats

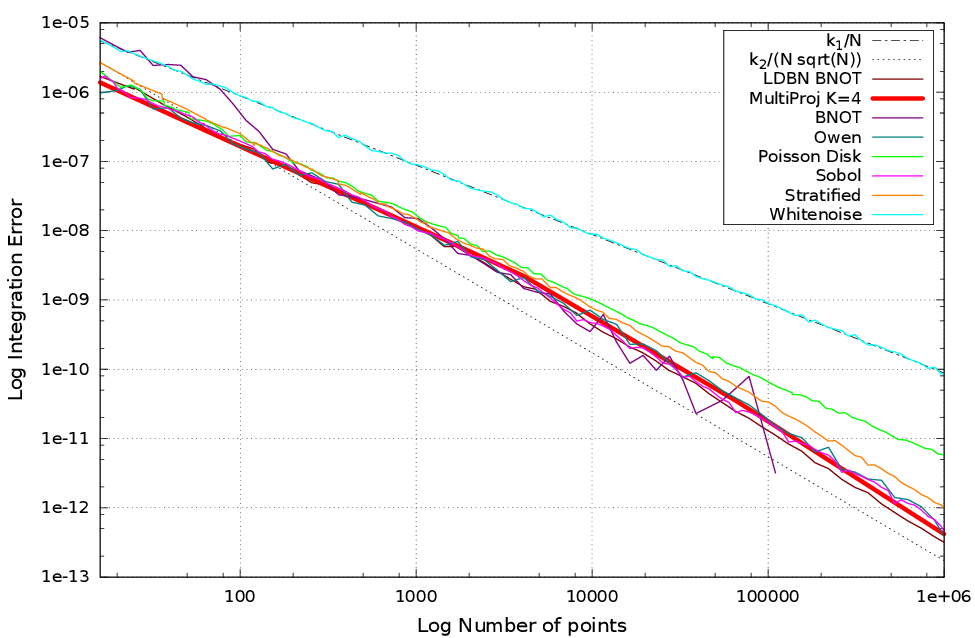
Résultats

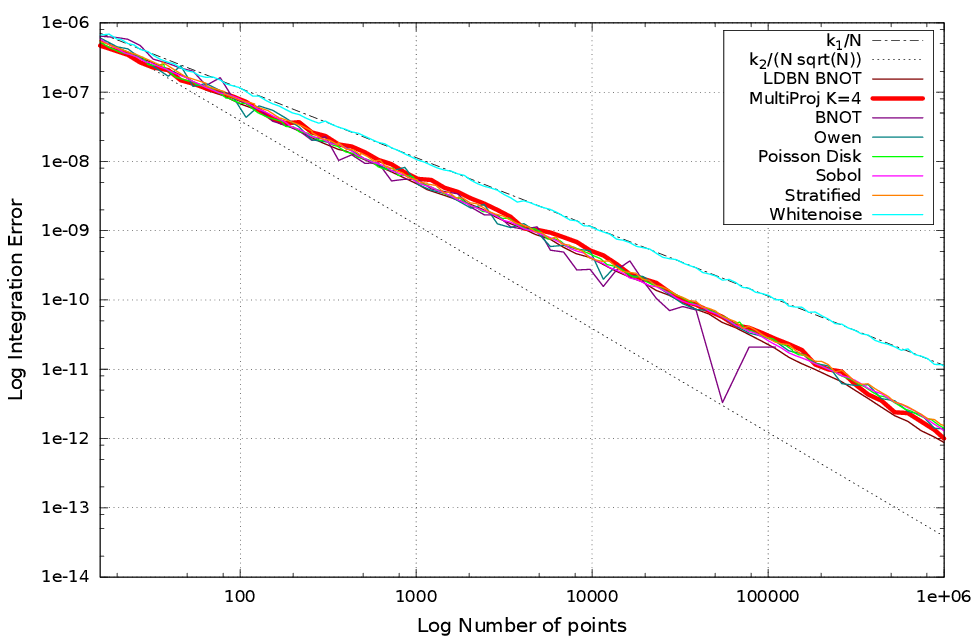
Résultats

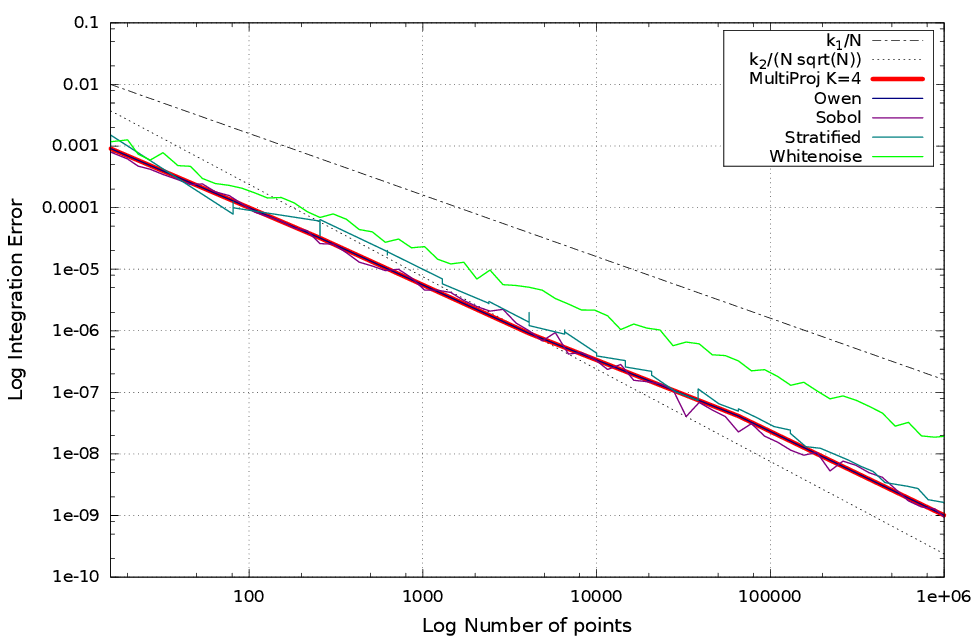
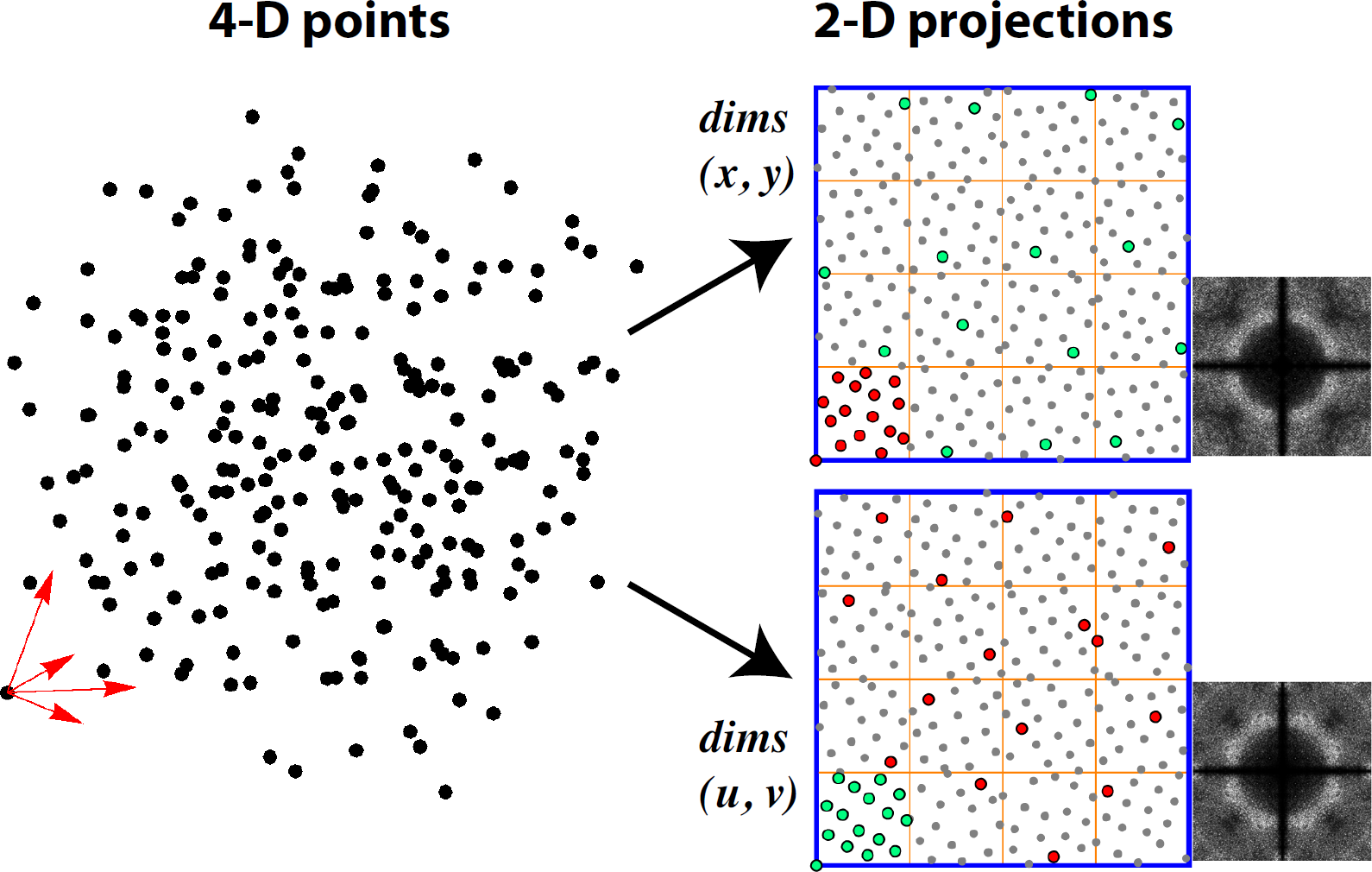
n-D

En fonction de $K$ on peut optimiser un certain nombre de dimensions.

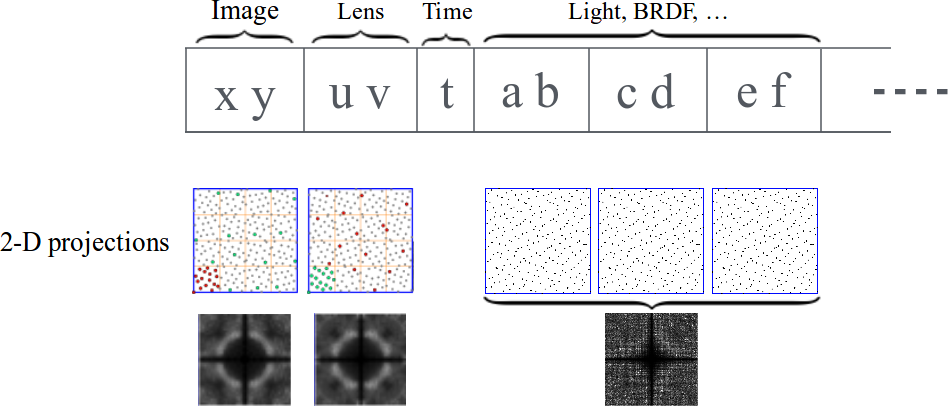
Résultats


Echantillons 4-D, 16 samples per pixel.
Stratified (MSE:0.0022) Sobol [Sob67] (MSE:0.0018) Owen's Scrambling [Owe95] (MSE:0.0017) MultiProj K=8 (MSE:0.0018)

Résultats


Echantillons 10-D, 16 samples per pixel.
Stratified (MSE:0.0017) Sobol [Sob67] (MSE:0.0015) Owen's Scrambling [Owe95] (MSE:0.0016) MultiProj K=8 (MSE:0.0013)

  • n-D
  • Très rapide, adaptative
  • Distribution bruit bleu par paires de dimension
  • Séquence
  • Basse discrépance dans les projections 2D uniquement
  • Bonne discrépance observée en n-D



  • Forcer le coté séquence et LDS dégrade le spectre (moins bien que LDBN par exemple)
  • Toujours un ensemble de permutations optimisées

Conclusion & perspectives

Conclusion

Combiner bruit bleu et basse discrépance est possible sans perte de qualité

En 2-D:
  • Bruit bleu
  • Basse discrépance
  • Rapide
    (4000 fois plus rapide que BNOT)[GBO+12]
En $d$-D:
  • Intérêt des projections
  • Bruit bleu et basse discrépance
  • Adaptatif
  • Sequentiel

... mais cela reste compliqué (pré-calculs, moins bonne qualité si séquentiel...)

Outils

  • Test d'unformité via mesure de discrépance (LDS)
  • Analyse fréquentielle
  • Analyse spatiale (stochastic point process)

Perspectives

  • Transport optimal comme mesure d'uniformité (fonctionne aussi sur des densités)
  • Exploitation du terme croisé intégrande/echantillonnage dans l'analyse spectrale (multiple importance sampling, cas non stationnaire...)
  • Caractère "bruit bleu" pas nécessaire en dimension $d$
  • ... mais critique dans les projcetions.
  • Corrélation des échantillons utilisés dans les estimateurs Monte-Carlo "pixels" dans le plan image

Le framework UTK !
Agrégation de tous les échantillonneurs et outils développés lors de cette thèse.

https://utk-team.github.io/utk/index.html