Laplace-Beltrami on Digital Surfaces
David Coeurjolly
CNRS, Université de Lyon



Material Sciences Applications



3SR Lab and CEN/CNRM - GAME URA 1357/Météo-France - CNRS
Up to $2048^3$
Laplace-Beltrami Operator
Digitization model
Given $\Shape \subset \R^d$, its digitization at gridstep $h$ is $$\DigF{\Shape}{h} = \left(\frac{1}{h} \cdot \Shape\right) \cap \Z^d$$

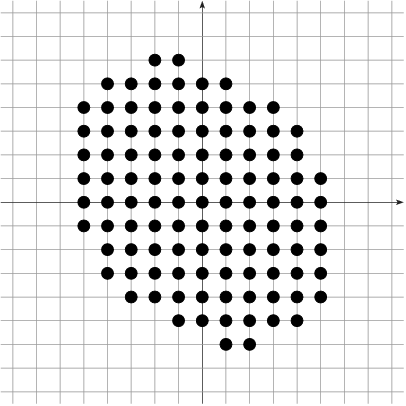

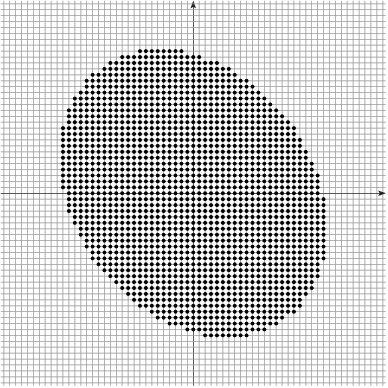
Example: $h^2|\DigF{\Shape}{h}|$ converges to the measure of $\Shape$ as $h\rightarrow 0$
[Gauss, Dirichlet, Huxley...]
Multigrid convergence of a local estimator
Given a digitization process $\AnyDig$, a local discrete geometric
estimator $\hat{E}$ of some geometric quantity $E$ is multigrid
convergent for the family of shapes $\Shapes$ if and only if, for any $\Shape
\in \Shapes$, there exists a grid step $h_\Shape>0$ such that the
estimate $\hat{E}(\AnyDig_{\Shape}(h),\hat{\vx},h)$ is defined for all
$\hat{\vx} \in \Bd{\Body{\AnyDig_{\Shape}(h)}{h}}$ with $0< h< h_\Shape$, and for
any $\vx \in \dS$,
$$
\forall \hat{\vx} \in \Bd{\Body{\AnyDig_{\Shape}(h)}{h}} \text{ with } \| \hat{\vx} -\vx\|_\infty
\le h, \quad\quad \color{myred}{|
\hat{E}(\AnyDig_{\Shape}(h),\hat{\vx},h) - E(\Shape,\vx) | \le \tau_{\Shape,\vx}(h)},
$$
where $\tau_{\Shape,\vx}: \R^{+} \setminus\{0\} \rightarrow \R^+$ has null limit at
$0$. The convergence is uniform for
$\Shape$ when every $\tau_{\Shape,\vx}$ is bounded from above by a function
$\tau_\Shape$ independent of $\vx \in \Bd{\Shape}$ with null limit at $0$.
Digital/Continuous mapping
-
The Hausdorff between $\partial \Shape$ and $\partial_h\Shape$ is
bounded by $\sqrt{d}h/2$
- For $d=2$, there exists an homeomorphism between $\partial X$ and $\partial_h X$
- For $d\geq 3$, no homeomorphism ☹, but
- Projection operator $\xi:\,\partial_h\Shape\rightarrow\partial \Shape$ is surjective
- Area of non-injective parts of $\xi$ the tends to zero
Digitization as an Hausdorff sampling of the continuous object
Can we estimate some differential properties (normal vectors, curvature, Laplace-Beltrami...) on digital surfaces with multigrid convergence properties ?
Motivations
\[ \Delta u = \nabla\cdot\nabla u \]
Key operator for many geometry processing tasks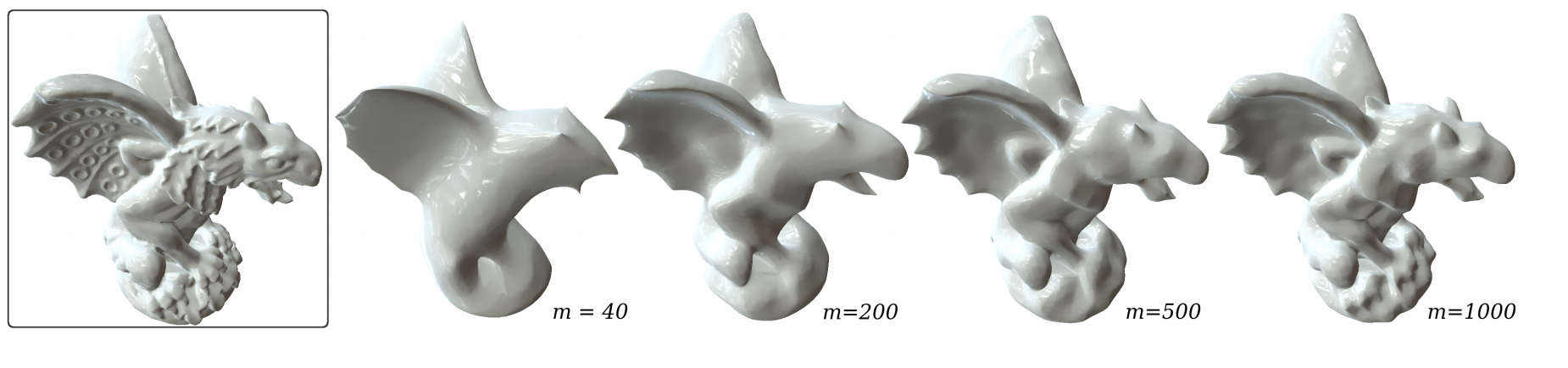

Discretization of the Laplace-Beltrami operator
Many discretization scheme for triangular meshes, polygonal
meshes, point clouds... | 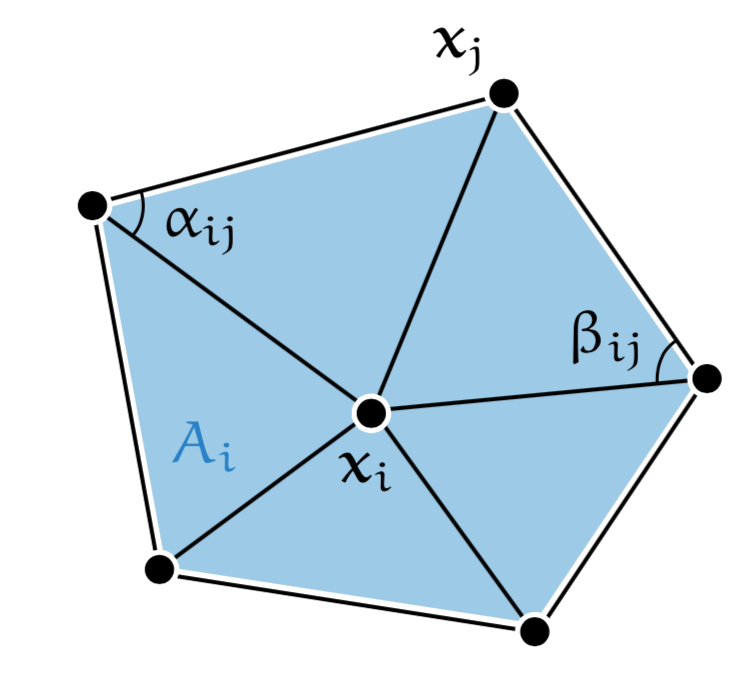 |
| SYM | LOC | LIN | POS | PSD | $C^2$-CON | |
|---|---|---|---|---|---|---|
| Mean Value | x | $\checkmark$ | $\checkmark$ | $\checkmark$ | x | x |
| Intrinsic Del | $\checkmark$ | x | $\checkmark$ | $\checkmark$ | $\checkmark$ | x |
| Combinatorial | $\checkmark$ | $\checkmark$ | x | $\checkmark$ | $\checkmark$ | x |
| Cotan | x | $\checkmark$ | $\checkmark$ | x | $\checkmark$ | x |
| Polygonal Lap. | x | $\checkmark$ | $\checkmark$ | x | $\checkmark$ | x |
| Convolutional | x | x | ? | $\checkmark$ | ? | $\checkmark$ |
| $r-$local | $\checkmark$ | x | ? | $\checkmark$ | ? | $\checkmark$ |
(update of "Discrete Laplace operators: No free lunch" [Wardetzky et al., 2007])
Strong consistency of the operator: $\quad\text{lim}_{\varepsilon \rightarrow 0} || \Delta_\varepsilon v - \Delta v ||_{L^\infty} = \text{lim}_{\varepsilon \rightarrow 0} \,\, \text{sup}_{x \in \partial M} | (\Delta_\varepsilon v) (x) - (\Delta v) (x) | = 0,\quad \forall v\in C^2(\partial M).$
What about Digital Surfaces ?
- No Laplace-Beltrami operator with strong consistency property exists on digital surfaces
- Anisotropic nature of digital surfaces may lead to geometrical inconsistencies


Heat equation based Laplace-Beltrami operator on meshes
$\Delta g(x,t) = \frac{\partial }{\partial t} g(x,t), u=g(•,0)\quad\rightarrow \quad $ $\Delta g(x,t) = \text{lim}_{t\rightarrow 0} \frac{1}{t}\int_{\partial M} p(t,x,y)(u(y)-u(x)) dy$
$$(\mathcal{L}_t\, u)(x) \EqDef \frac{1}{t (4 \pi t)^{\frac{d}{2}}} \int_{y \in \partial M} e^{- \frac{ ||y - x||^2 }{4 t}} (u(y) - u(x))dy,$$
As $t\rightarrow 0$, $(\mathcal{L}_t\,
u)$ converges to $\Delta\,u$.
$$(\mathcal{L}_{MESH}\, u)(p) \EqDef \frac{1}{4 \pi t^2} \sum_{f\in F} \frac{A_f}{3} \sum_{q \in V(f)} e^{- \frac{||p-q||^2}{4t}}\left(u(q) - u(p)\right)$$
If the mesh is a nice triangulation of a smooth
manifold, $(\mathcal{L}_{MESH}\, u)$ converges to $(\mathcal{L}_t\,
u)$
($t\approx$ 1/density).
Convolution based Laplace-Beltrami operator on Digital Surfaces
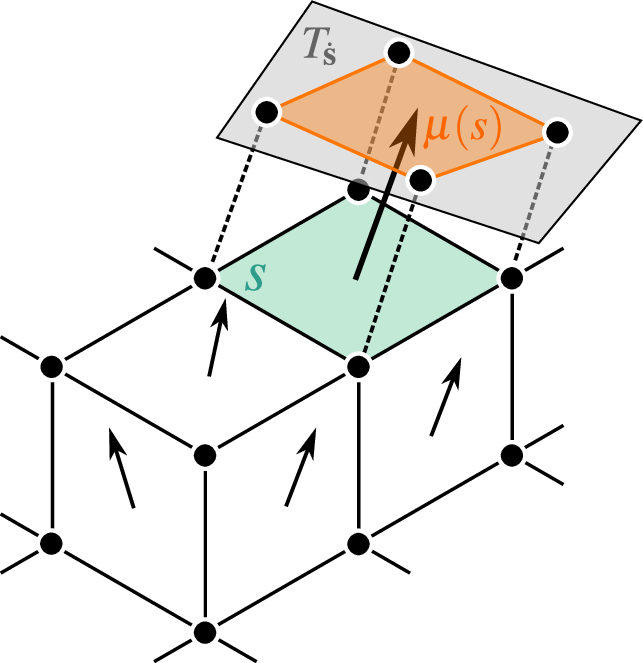
$$(L_h\, \tilde u)({\mathbf{s}}) \EqDef \frac{1}{t_h(4 \pi t_h)^{\frac{d}{2}}} {\color{mygreen}\sum_{\mathbf{r}\in S}} e^{- \frac{||{\mathbf{r}} - {\mathbf{s}}||^2}{4t_h}} [\tilde u({{\mathbf{r}}}) - \tilde u({{\mathbf{s}}})]{\color{myred} \mu(\mathbf{r})}$$
As $h\rightarrow 0$, $(L_h\, \tilde{u})$ converges to $\Delta\,u$.
($\tilde{u}$ is the extension of $u$ from $M$ to $\mathbb{R}^3$
along the normal vectors)
Measure of a surface element $\quad\mu(s)\EqDef \vn_s \cdot \vn_s^e$
Convolution based Laplace-Beltrami operator on Digital Surfaces
$$(L_h\, \tilde u)({\mathbf{s}}) \EqDef \frac{1}{t_h(4 \pi t_h)^{\frac{d}{2}}} {\color{mygreen}\sum_{\mathbf{r}\in S}} e^{- \frac{||{\mathbf{r}} - {\mathbf{s}}||^2}{4t_h}} [\tilde u({{\mathbf{r}}}) - \tilde u({{\mathbf{s}}})]{\color{myred} \mu(\mathbf{r})}$$
As $h\rightarrow 0$, $(L_h\, \tilde{u})$ converges to $\Delta\,u$.
($\tilde{u}$ is the extension of $u$ from $M$ to $\mathbb{R}^3$
along the normal vectors)
Sketch of the proof
Sketch of the proof
Sketch of the proof
Let $\mathbf{s} \in \partial_h M$, a function $u\in C^2(\partial M)$ and its extension $\tilde{u}$. For $t_h = h^{\alpha}$, $0 < \alpha \leq \frac{2}{2 + d}$ and $h \leq h_{max}$ with $h_{max}$ the minimum between $\text{Diam}(\partial M)$, $K_3(d, \alpha, \text{Diam}(\partial M))$ and $R / \sqrt{d+1}$, we have \begin{aligned}\\ | (\mathcal{L}_t u)(\xi({s})) - (\mathcal{L}_t \tilde{u})({s}) | \leq \text{Area}(\partial M) \,||\nabla u||_\infty \left[ K_1(d) h^{1 - \alpha(1 + \frac{d}{2})} + K_2(d) h^{2 - \alpha \frac{3 + d}{2}} \right] \end{aligned} with \[ K_1(d) \EqDef \frac{\sqrt{d+1}}{ 2^{d - 1} e \pi^{\frac{d}{2}}} \text{ and } K_2(d) \EqDef \frac{3 (d+1)}{ 2^{d + \frac{5}{2}} \sqrt{e} \pi^{\frac{d}{2}}} . \]
Technical proof using the regularity of $u$ and Hausdorff distance between $\partial M$ and $\partial_h M$.
Sketch of the proof
Sketch of the proof
Let $ M $ be a compact domain whose boundary has positive reach $R$. For $h \leq \frac{R}{\sqrt{d+1}}$,
the digital integral is multigrid convergent toward the integral over $\partial M $.
More precisely, for any measurable function $f : \mathbb{R}^{d+1} \rightarrow \mathbb{R}$, one gets
$$
\,\\ \Bigg| \int_{\partial M } f(x)dx - \text{DI}_h(f,{ M }_{h},\hat{\mathbf{n}}) \Bigg|
\leq 2^{d + 3} (d+1)^{\frac{3}{2}} \ Area (\partial M ) \Big( \text{Lip}(f) \sqrt{d + 1} \ h \\
\phantom{dfqfijeiofjqzdjiqjziieqioj} + ||f||_\infty \cdot {\color{mygreen}||\hat{\mathbf{n}} - \mathbf{n}||_{est}}\Big),
$$
($\text{DI}_h(f,{ M }_{h},\hat{\mathbf{n}})\approx$ summation of $f$
evaluated at
each surfel $s$ and weighted by $\mu(s)$)
Remaining steps: We set $f(x) \EqDef \frac{1}{t_h (4 \pi t_h)^{\frac{d}{2}}} e^{- \frac{||{x} - {s}||^2}{4t_h}}(\tilde u({x}) - \tilde u({s}))$ and we derive bounds for $\text{Lip}(f)$ and $||f||_\infty$.
Main result
Let $\mathbf{s}$ be a surfel in $\partial_h M$, a function $u \in C^2(\partial M)$ and its extension $\tilde u$. Let $t_h = h^\alpha$ and let the convergence speed of the normal estimator be in $O(h^\beta)$. Let $h_0$ be the minimum between $\text{Diam}(\partial M)$, $R / \sqrt{d+1}$ and $K_3(d, \alpha, \text{Diam}(\partial M))$. For $0 < h \leq h_0$ we have
$$\\ \,\\ \lim\limits_{h \rightarrow 0} |{(\Delta u)(\xi({s})) - (L \tilde{u})({s})}| = 0 $$
if $0 < \alpha < \min\left( \frac{2}{d + 2}, \frac{2 \beta}{d + 1} \right)$.
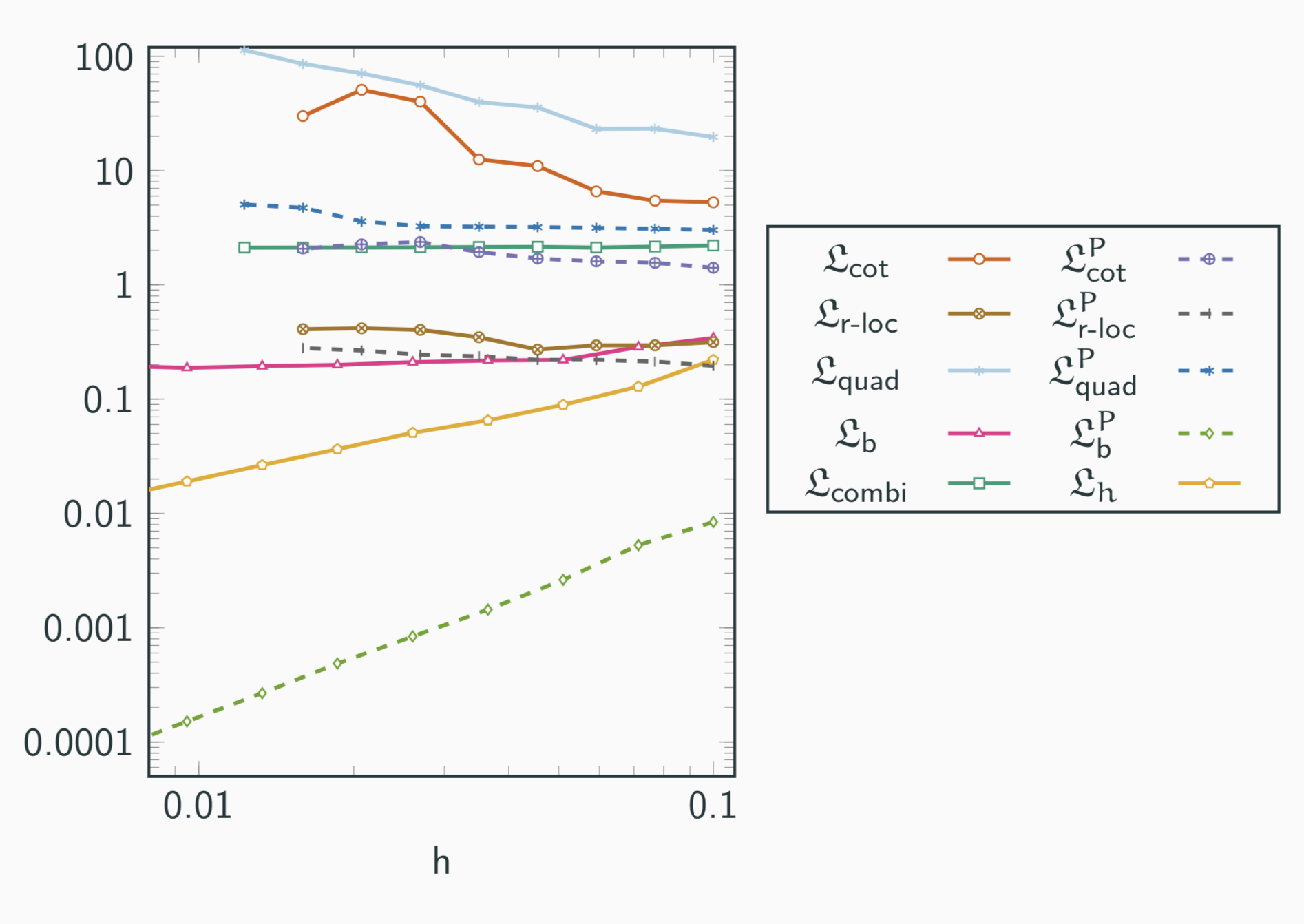




In summary
- Strong consistency thanks to a multigrid convergent normal vector field
- Discrete operator is not as sparse as the cotangent one
- Efficient implementation (convolutions on compact support)