Point Sampling in Monte Carlo Rendering














David Coeurjolly









Context

Image rendering: simulate light transport

[Kaj76] $$\mathcal{I}(\vx) = L_e(\vx) + \int_\mathcal{H} \rho(\vp, \vx) \mathcal{I}(\vp) d\vp$$

Numerical approximation

Monte Carlo Estimation

$$\int_D f(x)dx \approx \frac{1}{n} \sum_{i=0}^{n} f(x_i)$$

Monte Carlo Estimation

$$\int_D f(x)dx \approx \frac{1}{n} \sum_{i=0}^{n} f(x_i)$$

Monte Carlo Estimation

$$\int_D f(x)dx \approx \frac{1}{n} \sum_{i=0}^{n} f(x_i)$$

Material Design


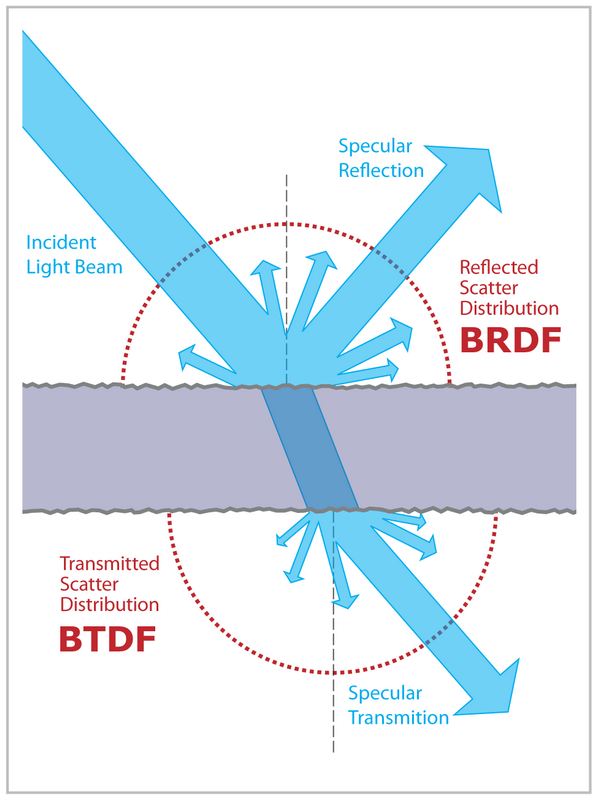
We need samples in n-D

Many strategies

  • for path construction (bidirectional, gradient domain...)
  • to sample the n-D space (adaptive, importance sampling, multiple importance sampling...)
  • to correlate samples from one pixel to a neighboring one
  • to post-filter/reconstruct the final image
  • ...

We need fast samplers

Error, Bias, Variance

$\mathcal{I} = \int_\Omega fdx$

$\mathcal{I}_n = \frac{1}{n}\sum f(x_i), \quad \{x_i\}\in \Omega$

$$ \Delta := | \mathcal{I} -\mathcal{I}_n | $$

$$ \langle \Delta\rangle := \mathcal{I} - \langle \mathcal{I}_n \rangle $$

$$ \text{Var}(\mathcal{I}_n) := \langle \mathcal{I}_n^2 \rangle - \langle \mathcal{I}_n \rangle^2 $$

Convergence speed

1spp
2spp
4spp
8spp
16spp
32spp
64spp
128spp
256spp
full

Four main classes


[Shi91]
(Poisson process, stratified Poisson,...)

[Hal64]                 [HH64]                 [Sob67]
(Hammersley, Halton, Sobol,...)

[Coo96]                 [Bri07]                 [MF92]
(Sampling with proximity constraints)

[GBO+12]              [CYK+12]                [Fat11]
(Energy based formulations)

Whitenoise / Poisson process

$$ Var(I_n) = O\left(\frac{\sigma_f^2}{{n}}\right) $$

Poisson disk / Dart throwing

Higher quality for low sample counts but... $$ Var(I_n) = O\left(\frac{1}{{n}}\right) $$ {demo}

van der Corput 1d Sequences (whiteboard)

Low discrepancy sequences / Halton

E.g.: $x(n)=(g_{{b_{1}}}(n),\dots ,g_{{b_{s}}}(n))$ in dimension $s$ and $b_1,\ldots,b_{s-1}$ arbitrary coprime integers
$g_{b}(n)=\sum _{{k=0}}^{{L-1}}d_{k}(n)b^{{-k-1}}.$ (b-ary representation of the positive integer expressed in fractional part)

$$ \Delta = O\left(\frac{ \log(n)^{d-1}}{n}\right) $$ {demo}

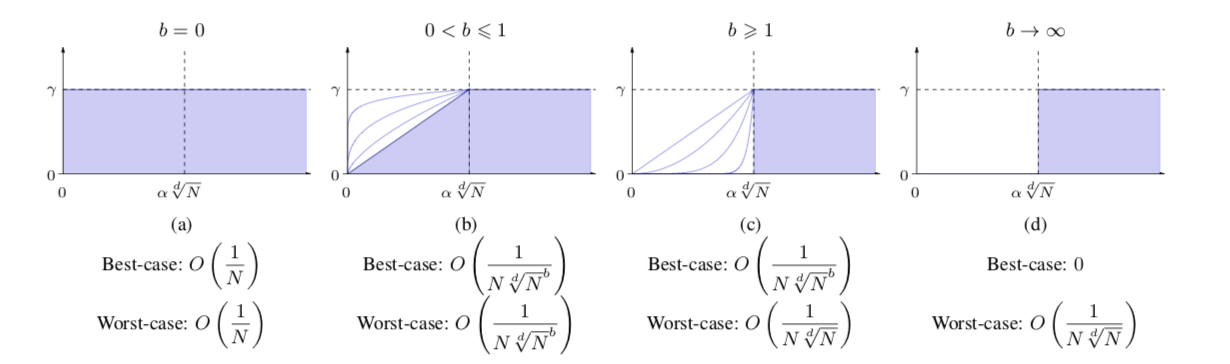
Few convergence speeds

$n$ samples dans $[0,1)^d$


$$ Var(I_n) = O\left(\frac{\sigma_f^2}{{n}}\right) $$


$$ \Delta = O\left(\frac{ \log(n)^{d-1}}{n}\right) $$


$$ Var(I_n) = O\left(\frac{1}{n\sqrt[d]{n}} \right) $$

Aliasing and error structure

Aliasing and error structure

Aliasing and error structure

Wrap-up

Sampling process:

  • Uniform in $[0,1)^d$
  • With asymptotic bounds on the variance reduction for MC / QMC
  • Stochastic processes but with correlation between samples

Image rendering context:

  • Reatively limited number of dimensions (~30/40)
  • As few as possible structure (aliasing)
  • As efficient as possible even for low sample count
  • Fast and progressive sampler

Evaluation tools

Discrepancy

Evaluate the uniformity of a point set $P_n$

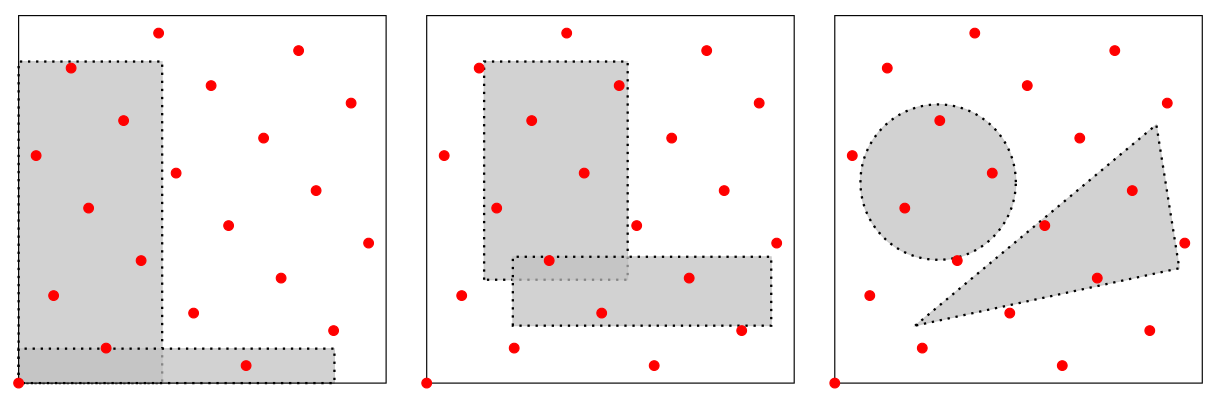
Star
discrepancy		 Extreme discrepancy Isotropic discrepancy
$\mathcal{D}_*(P_n) := \sup_{\vv \in [0, 1)^d} \left| v_1 \cdots v_d - \alpha( P_n, \vv ) \right| $
$$ \Delta \leq \mathcal{D}_*(P_n)V(f) $$

$f$ is an Hardy & Krause bounded variation function.

Discrepancy

A sampler is low discrepancy if its discrepancy is in $O\left(\frac{\log(n)^{d-1}}{n}\right)$.

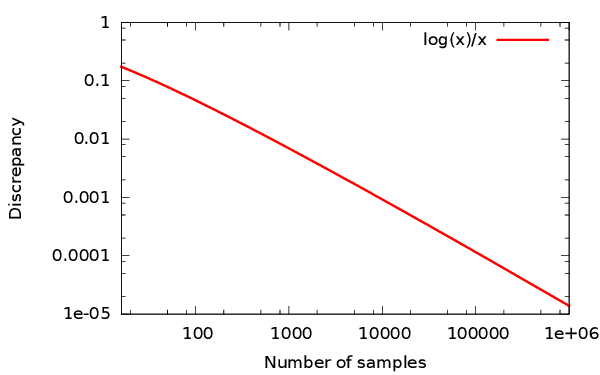
$$ \Delta = O\left(\frac{ \log(n)^{d-1}}{n}\right) $$ (for finite HK-BV integrand compared to $O(1/\sqrt{n})$ for Poisson sampler)

QMC sampler examples

Given $i\in\mathbb{N}$, $$ i = (\ldots a_2a_1a_0)_2$$ $$\phi(i) = (.a_0a_1a_2\ldots)_2 = \sum_k a_k 2^{-(k+1)} \in [0,1)$$

E.g. $i=11 = (1011)_2$, $\phi(i)=(.1101)_2 = \frac{1}{2} + \frac{1}{4} + \frac{1}{16} = 0.8125 \in[0,1)$

$$ \left\{\left( \phi(i), \frac{i}{n}\right )\right\}\in [0,1)^2$$
Representation of the index $i$ on coprime bases $\{b_j\}$, invert the digits and reinterpret as fractions to generate a sample in $[0,1)^s$

arithmetic on $\mathbb{Z}/p\mathbb{Z}$...

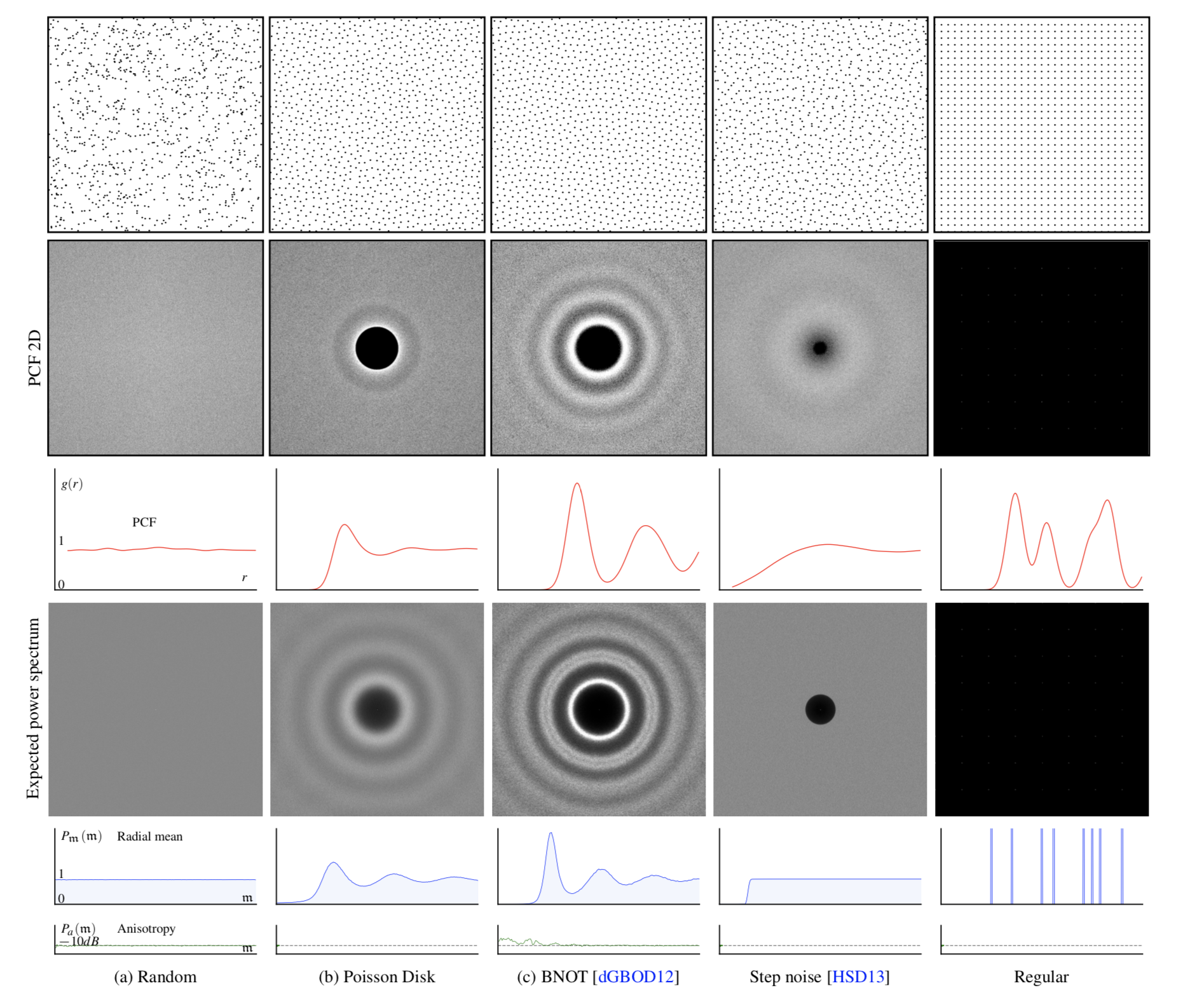
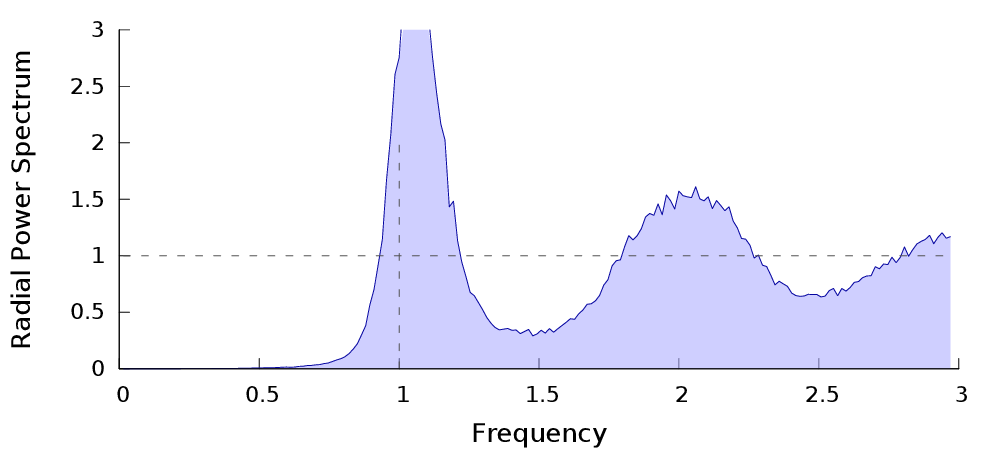
Spectral Analysis

$P_n$ Power spectrum Radial Power Spectrum

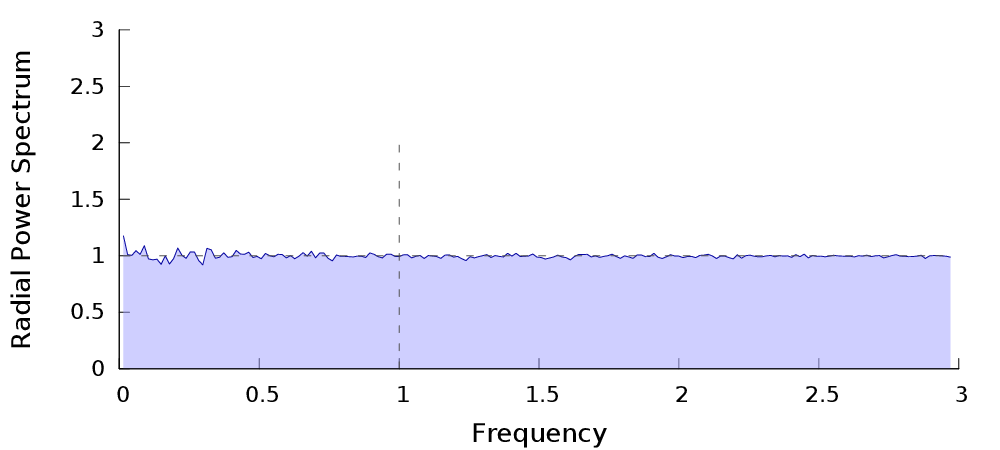
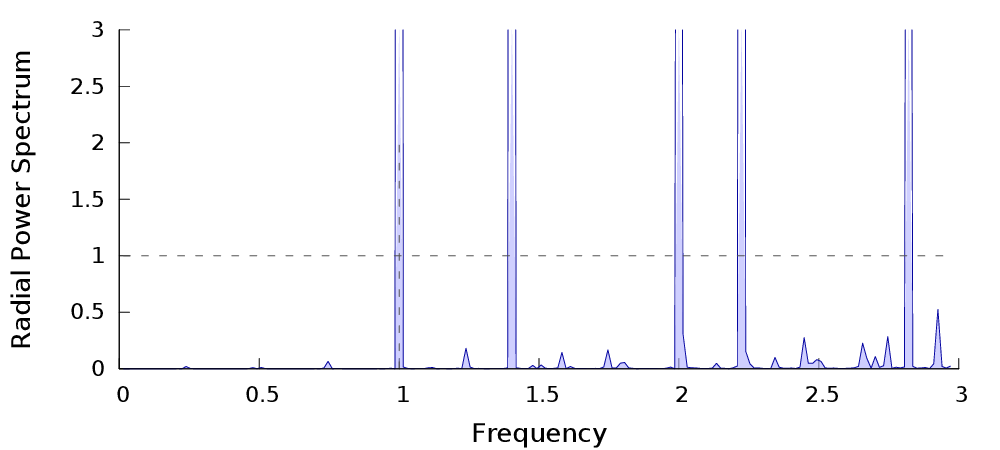
Spectral Analysis

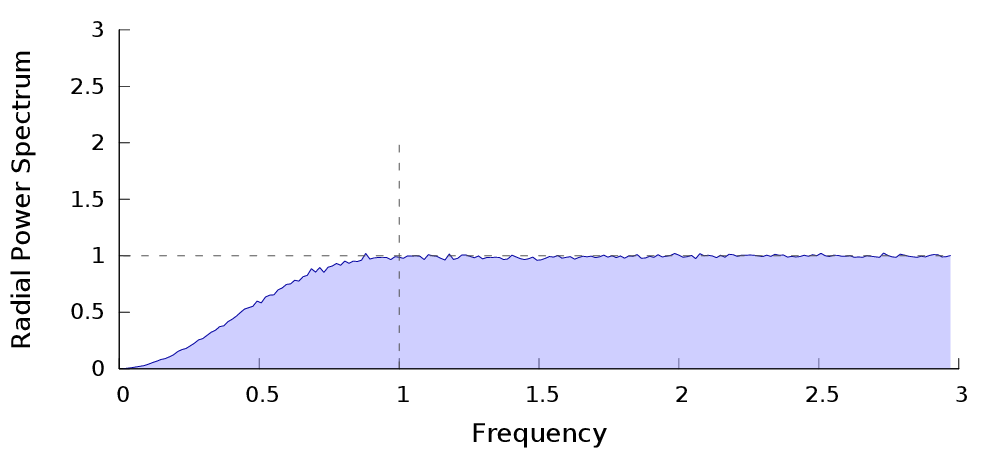Spectral peaks are harmful for MC but also for signal reconstruction
$sin(x^2 + y^2)$

Analysis

$$S(x) = \frac{1}{n}\sum_{k=1}^n \alpha_k \delta(x-x_k)\quad \text{and its $m$-th Fourier series coefficient}\quad \mathbf{S}_m = \frac{1}{n}\sum_{k=1}^n \alpha_k e^{-i2\pi m x_k}\,,$$ we have $$\mathcal{I}_n=\int_0^1 f(x)S(x)dx = \int_\mathbb{R} \mathcal{F}_f(v)\mathcal{F}_S(v)dv =\sum_{m=-\infty}^{\infty} \mathbf{f}_m^* \mathbf{S}_m$$

If $S(x)$ is a stochastic point process:


$$\langle \Delta \rangle = \mathbf{f}_{0}^*(1 - \langle \mathbf{S}_0\rangle) - \sum_{m\in\mathbb{Z}, m\neq 0} \mathbf{f}_m^*\langle \mathbf{S}_m\rangle$$ $$Var({I}_n) = \mathbf{f}_0^*\mathbf{f}_0 Var(\mathbf{S}_0) + \sum_{m\in\mathbb{Z}, m\neq 0}\mathbf{f}_m^*\mathbf{f}_m\langle \mathbf{S}_m^*\mathbf{S}_m\rangle + \sum_{m \in \mathbb{Z}}\sum_{l \in \mathbb{Z}, l\neq m} \mathbf{f}_m^*\mathbf{f}_l\langle \mathbf{S}_m^*\mathbf{S}_l\rangle$$

$\langle \Delta \rangle = \mathbf{f}_{0}^* - \sum_{m\in\mathbb{Z}, m\neq 0} \mathbf{f}_m^*\langle \mathbf{S}_m\rangle$
$\langle \Delta \rangle = 0$ for Poisson process (or any unbiased sampler)

$Var({I}_n) =\sum_{m\in\mathbb{Z}}\mathbf{f}_m^*\mathbf{f}_m\langle \mathbf{S}_m^*\mathbf{S}_m\rangle$

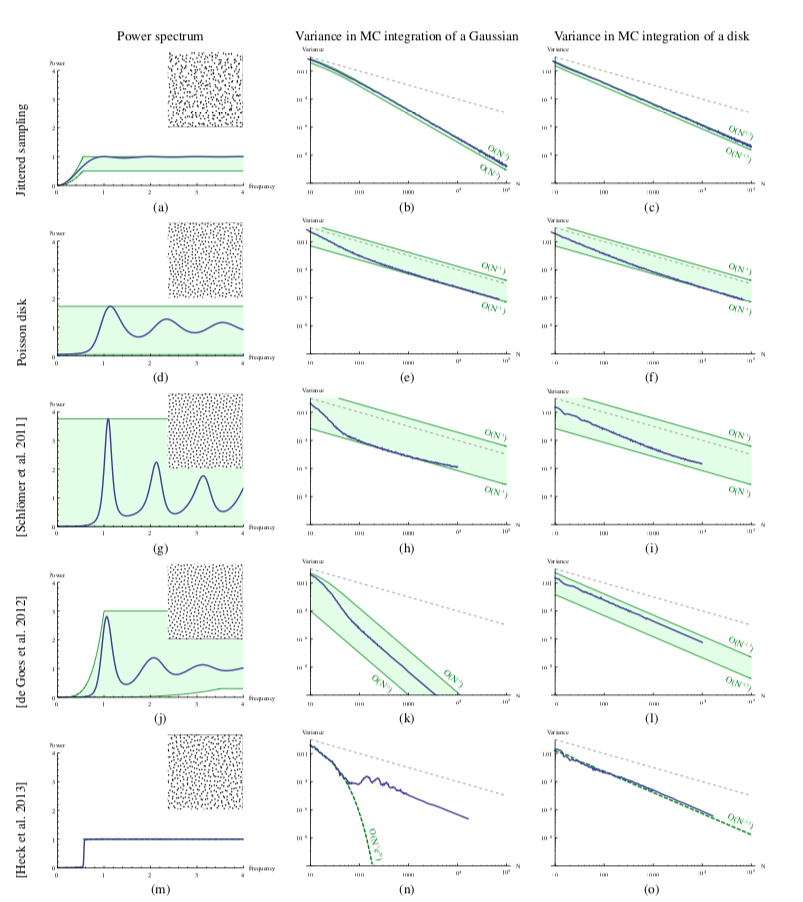
Spectral Analysis

$Var({I}_n) =\sum_{m\in\mathbb{Z}}\mathbf{f}_m^*\mathbf{f}_m\langle \mathbf{S}_m^*\mathbf{S}_m\rangle$

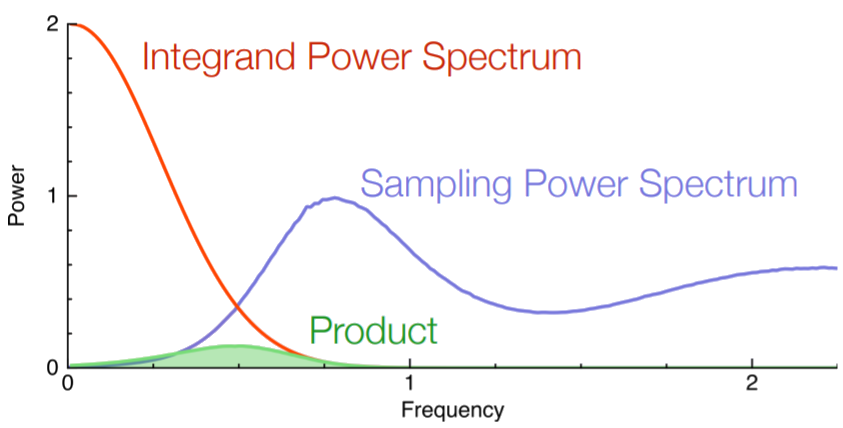
Spectral Analysis

$Var({I}_n) =\sum_{m\in\mathbb{Z}}\mathbf{f}_m^*\mathbf{f}_m\langle \mathbf{S}_m^*\mathbf{S}_m\rangle$

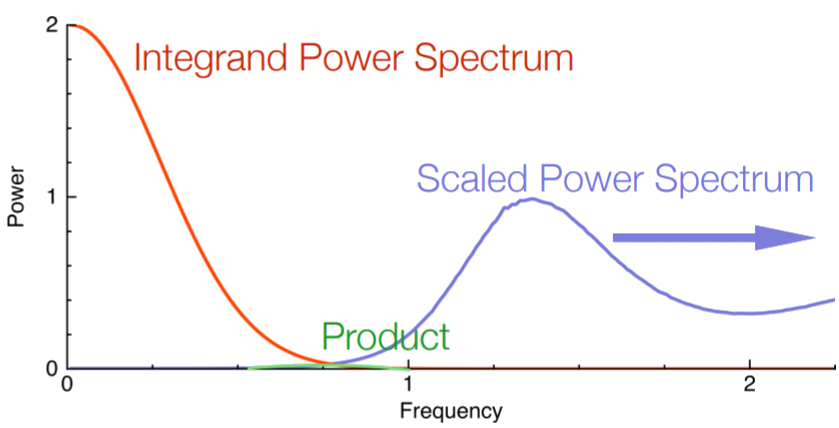
High variance reduction = low energy in the low frequency domain of the sampler






Optimal Transport



Distance between a discrete measure (point pattern = set of Diracs) and a measur (e.g. Uniform measure).

$\Rightarrow$ cf SOT

Related characterizations



Pair Correlation Function, Differential Analysis...

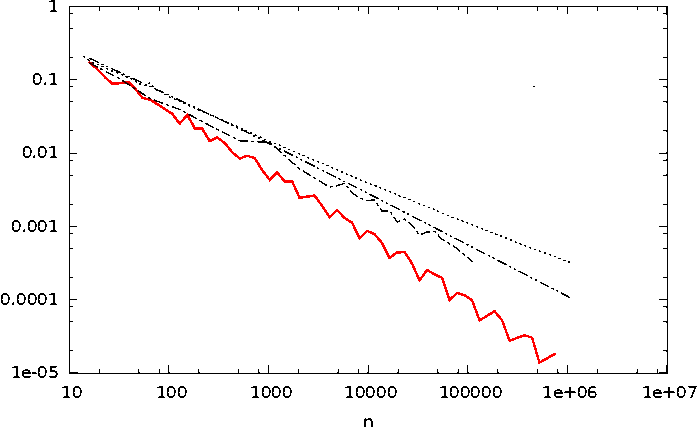
Few convergence speeds

$n$ samples dans $[0,1)^d$


$$ Var(I_n) = O\left(\frac{\sigma_f^2}{{n}}\right) $$


$$ \Delta^2 = O\left(\frac{ \log(n)^{2(d-1)}}{n^2}\right) $$


$$ Var(I_n) = O\left(\frac{1}{n\sqrt[d]{n}} \right) $$

The Ideal Sampler in CG

  • Uniform in $[0,1)^d$
  • With highest asymptotic variance reduction in MC / QMC integration

For rendering:

  • Rather limited number of dimensions (~30/40)
  • No structure or patterns (for aliasing issues)
  • Low error for low sample counts
  • Fast sampler and progressivity

LDS + BN



https://utk-team.github.io/utk/index.html

Polyhex





[WPC+14] Florent Wachtel, Adrien Pilleboue, David Coeurjolly, Katherine Breeden, Gurprit Singh, Gaël Cathelin, Fernando de Goes, Mathieu Desbrun, Victor Ostromoukhov. Fast Tile-Based Adaptive Sampling with User-Specified Fourier Spectra. ACM Transactions on Graphics (Proceedings of SIGGRAPH), 33(4):56:1-56:11, August 2014.

Aperiodic tile-based system

  • Precomputed samples in a hierarchical tiling system for fast blue noise sampling (+ 1 million samples/sec)
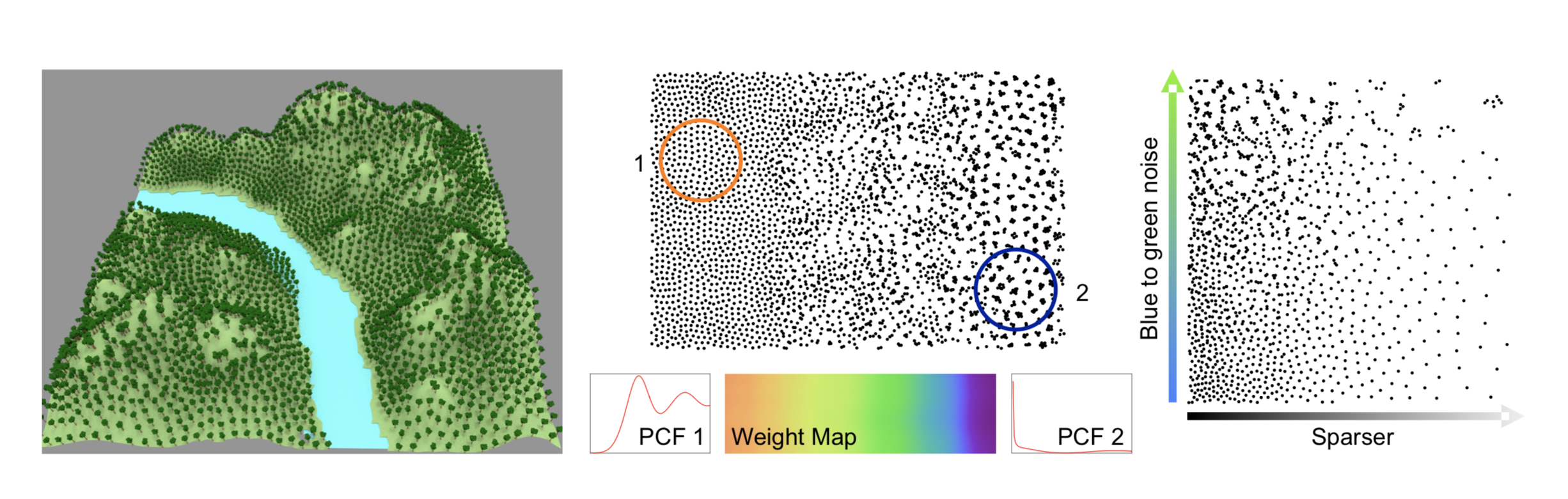
  • Local density control

  • 2D
  • Extremely fast
  • High quality blue noise
  • Adaptive sampling



  • 2D only
  • Huge precomputed LUT

Low Discrepancy Blue Noise

Low discrepancy Blue Noise in 2D

      
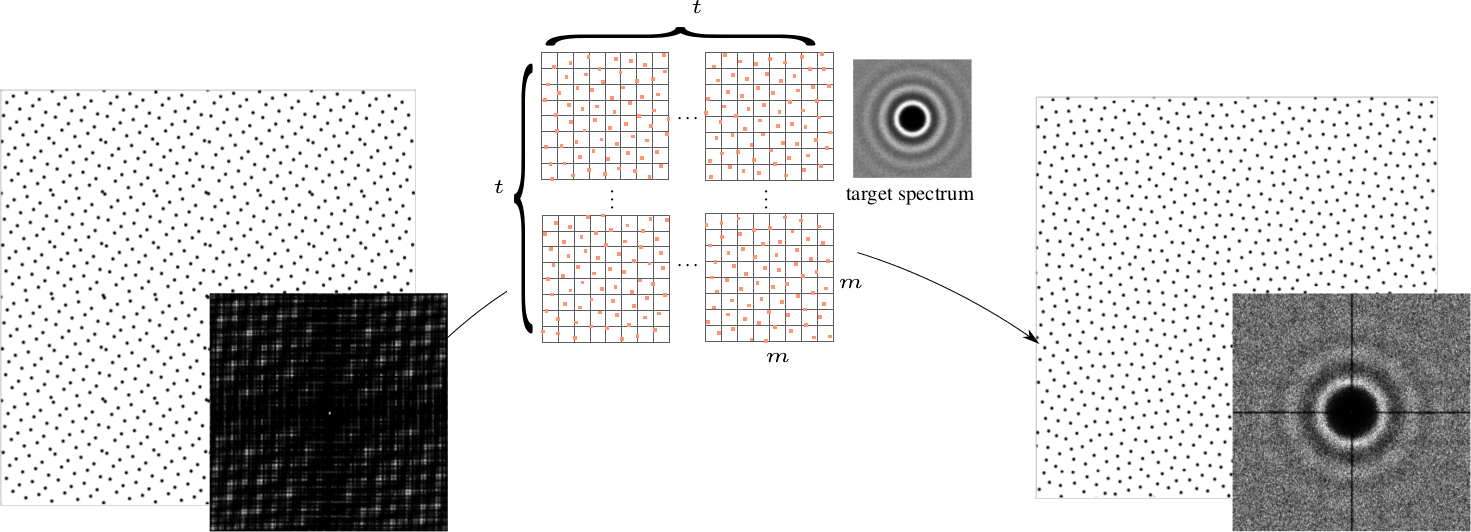
[APC+16] Ahmed A., Perrier H., Coeurjolly D., Ostromoukhov V., Guo J., Dongming Y., Hui H., Deussen O.. Low discrepancy blue noise sampling. ACM Transactions on Graphics (Proceedings of ACM SIGGRAPH Asia 2016), 2016.

The method

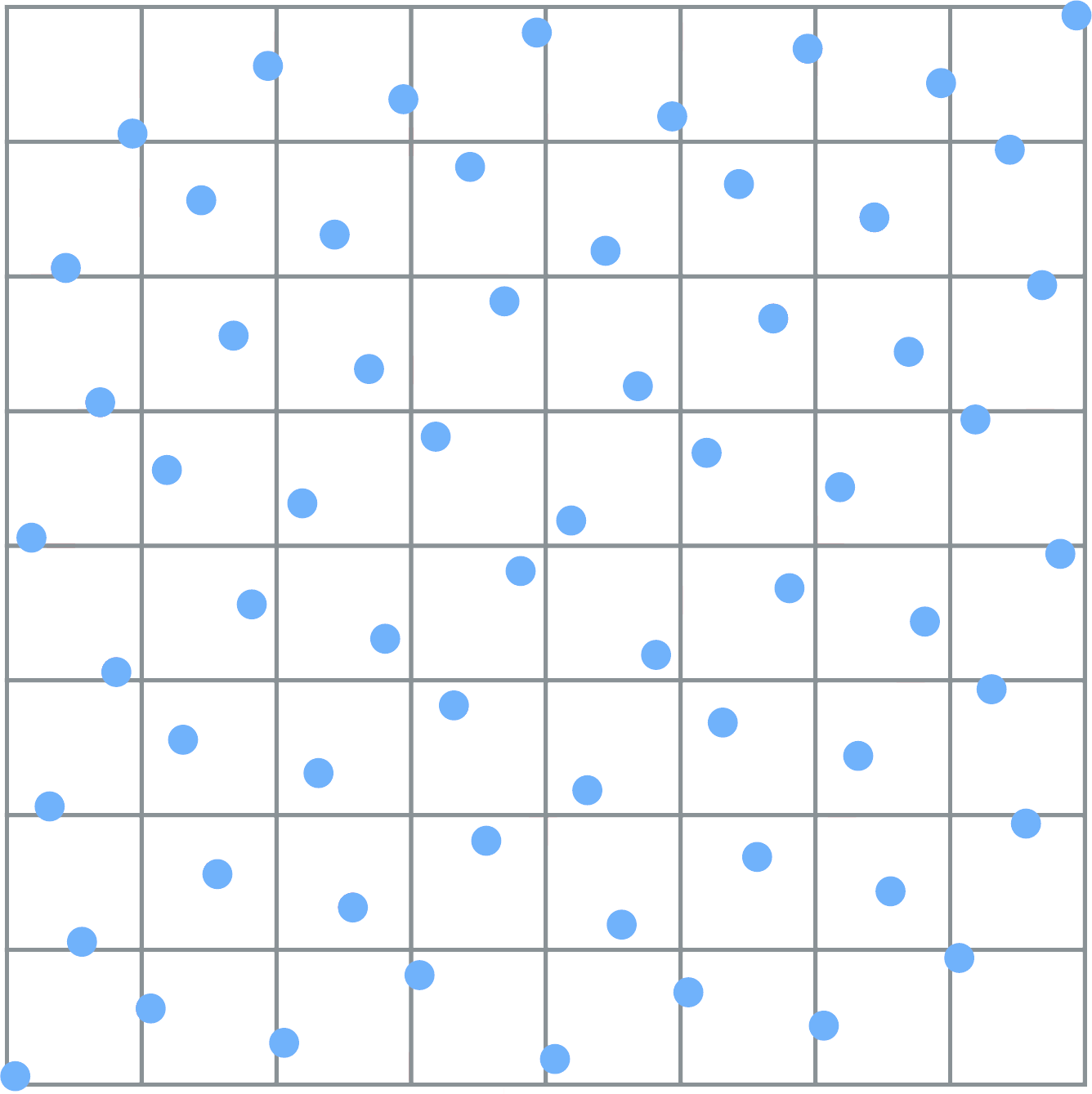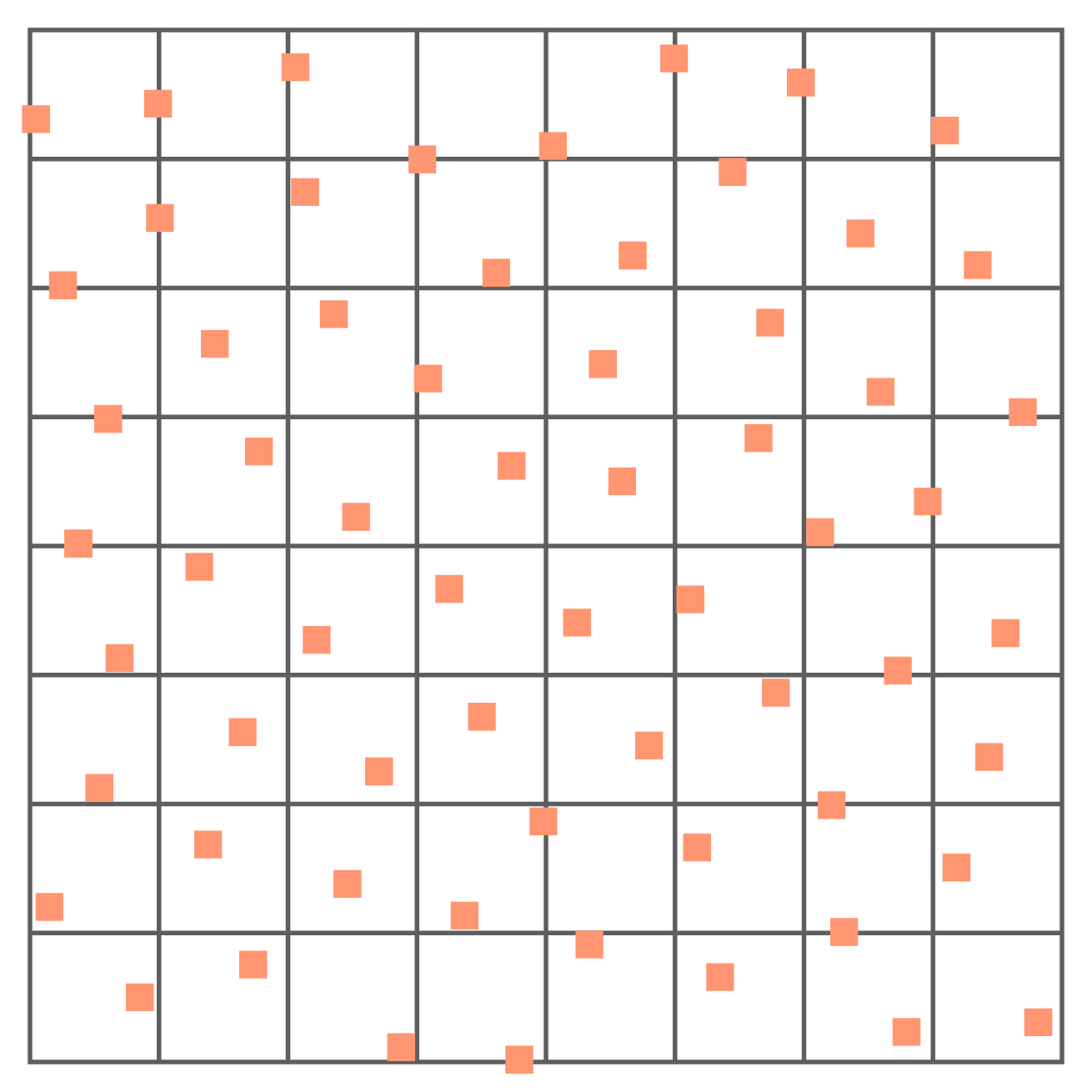The method

The method

On calcule les permutations de taille $m$ à partir d'un ensemble de taille $t^2$. On les stocke ensuite dans une LUT pour générer des ensembles de taille $n$.

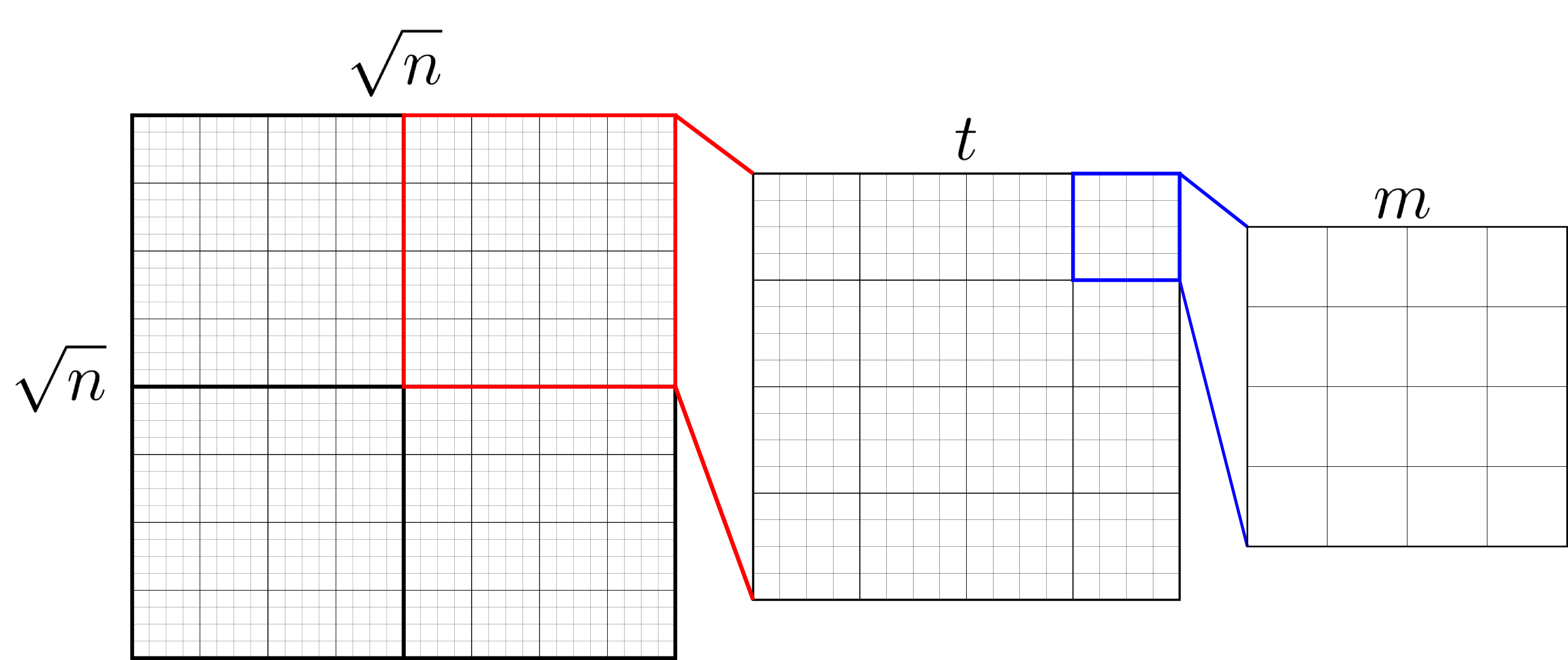
$$ \lbrace X + \phi(Y - Y\%m + L_X), \\ Y + \phi(X - X\%m + L_Y) \rbrace $$

The method

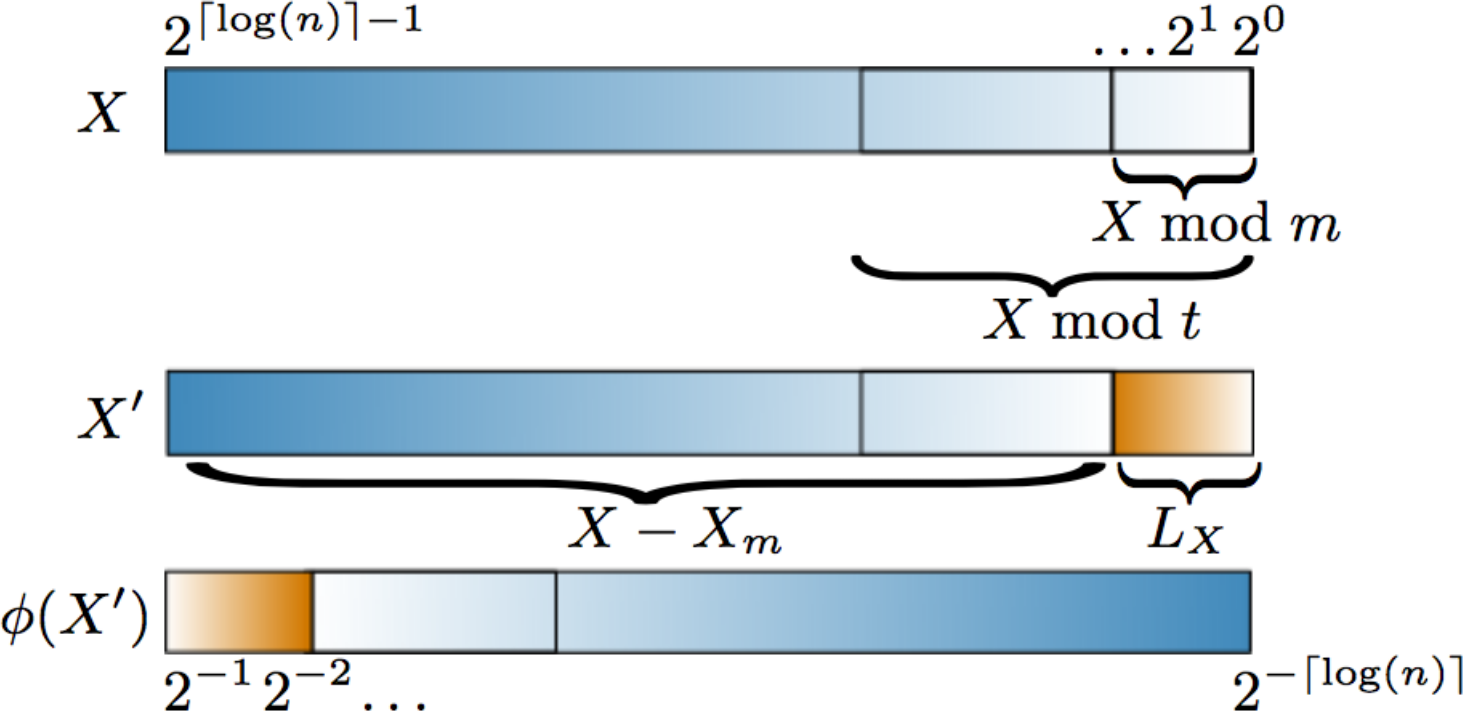
$$ \lbrace X + \phi(Y - Y\%m + L_X), \\ Y + \phi(X - X\%m + L_Y) \rbrace $$
Si $t$ est trop petit p/r à $n$, les permutations vont se répéter et les caractéristiques fréquentielles de l'ensemble de points vont se dégrader. Si $m$ est trop petit p/r à $t$, le spectre sera mal préservé.

The method

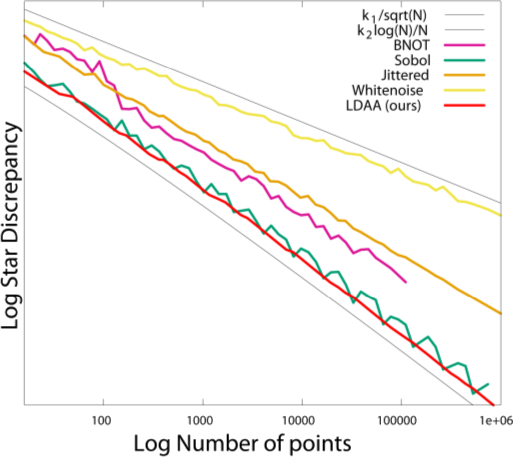
Results

BNOT [GBO+12] Sobol [Sob67]
Owen's Scrambling [Owe95] LDBN ($m=16$, $t=128$)

Results

BNOT [GBO+12] LDBN ($m=16$, $t=128$)
Step [HSD13] LDBN ($m=16$, $t=128$)

Results

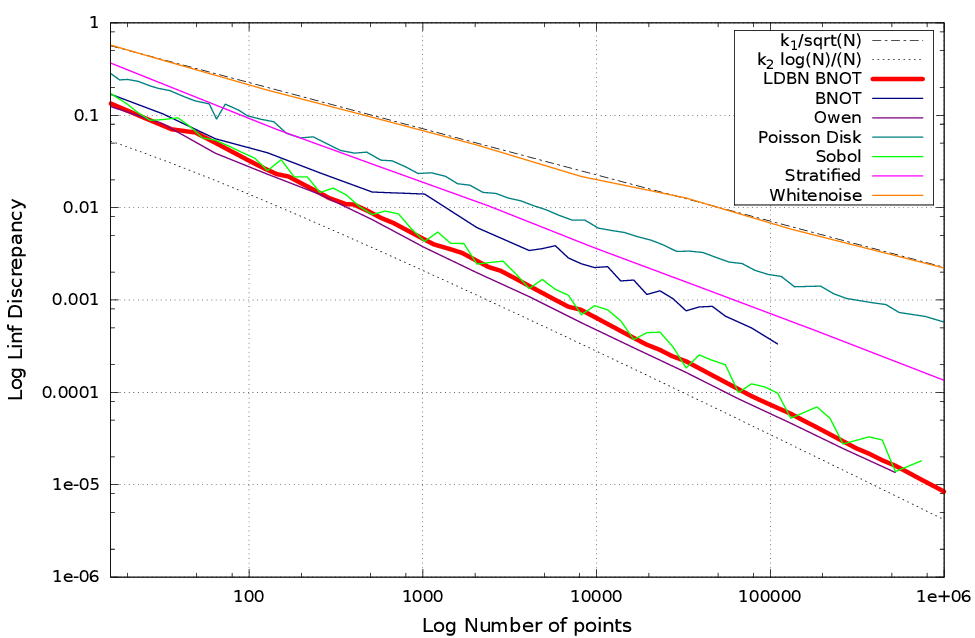
Results

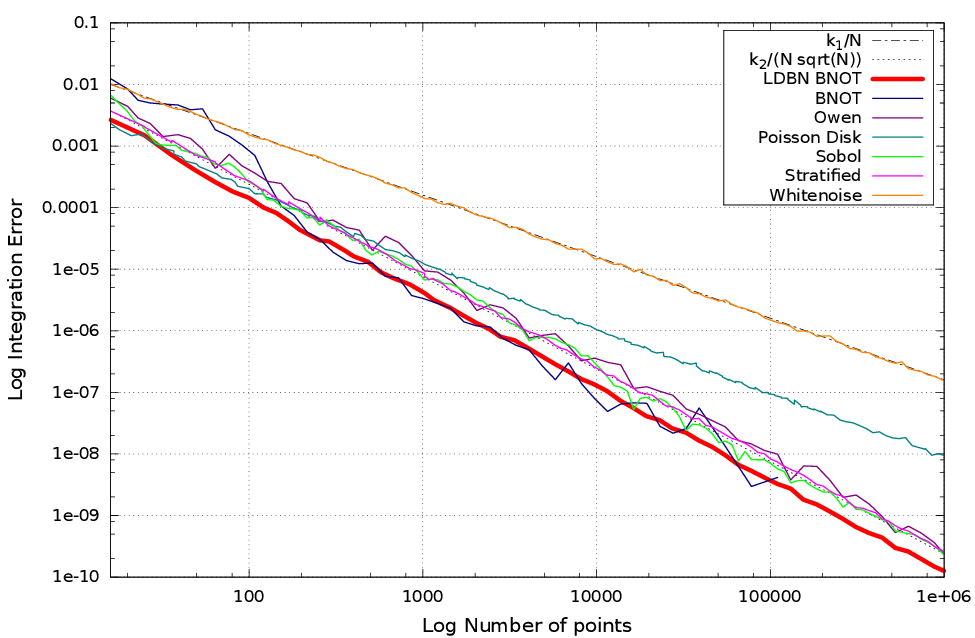
Results

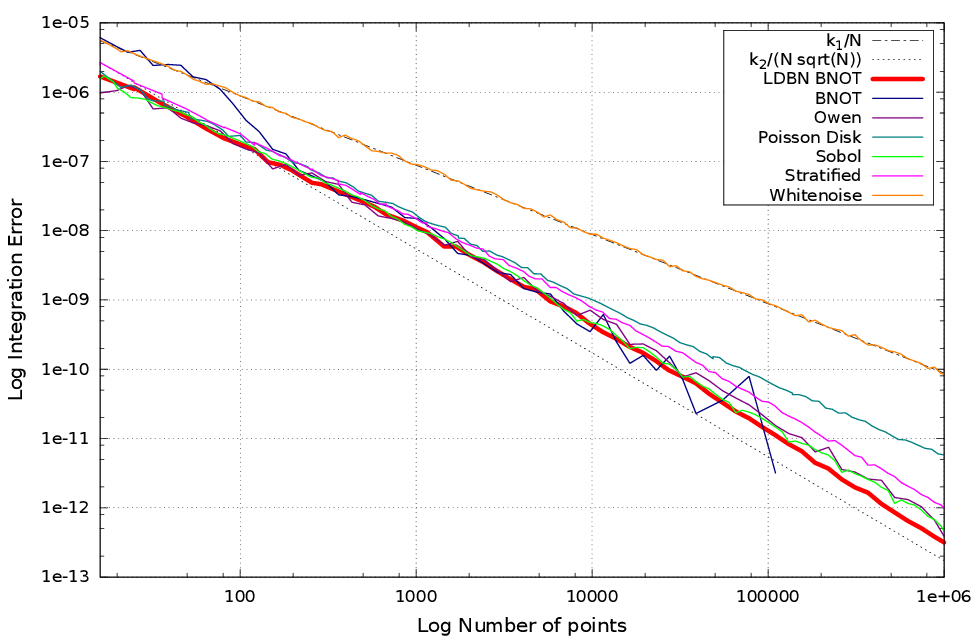
Results

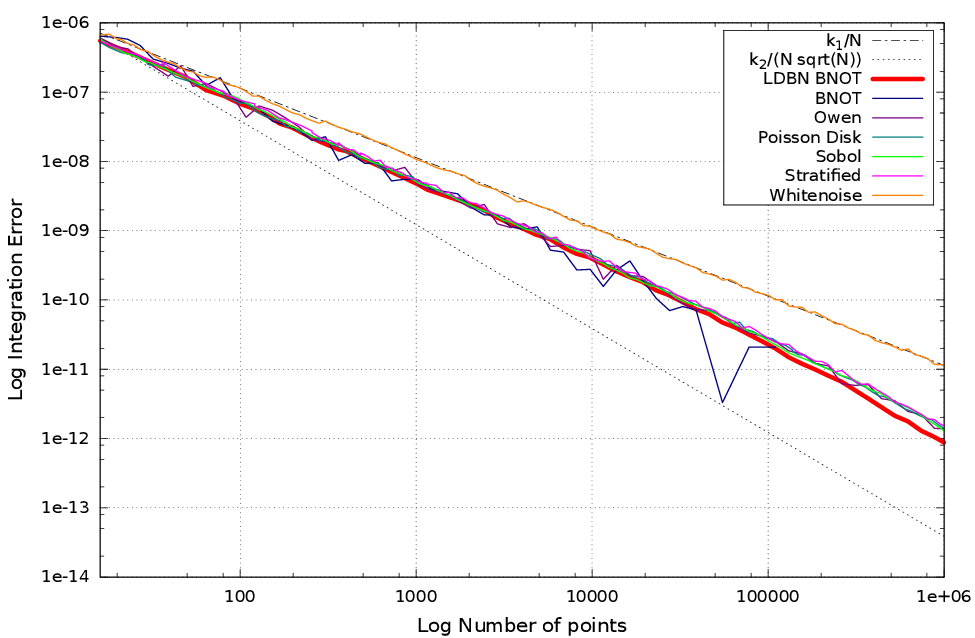
Results

BNOT [GBO+12] Sobol [Sob67] Owen's Scrambling [Owe95] LDBN ($m=16$, $t=128$)

  • 2D
  • Extremely fast
  • Very good blue noise distribution
  • Low discrepancy point set



  • 2D ony
  • Not a sequence

Sequences with Low-Discrepancy Blue-Noise 2-D Projections

Main idea

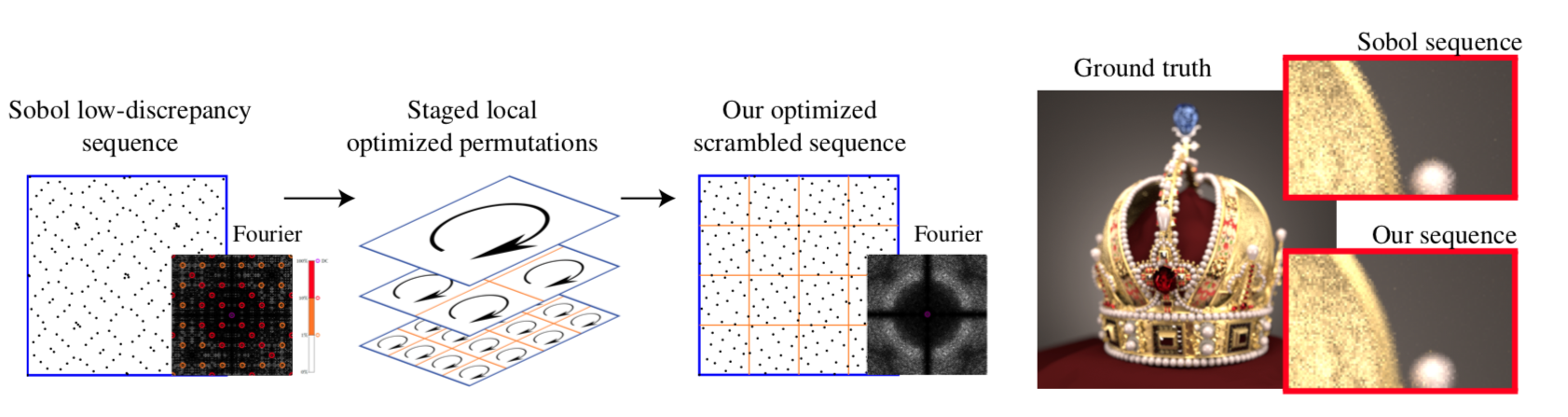
[PC+18] Hélène Perrier, David Coeurjolly, Feng Xie, Matt Pharr, Pat Hanrahan, Victor Ostromoukhov. Sequences with Low-Discrepancy Blue-Noise 2-D Projections. Computer Graphics Forum (Proceedings of Eurographics), 37(2), 2018.

Owen's scrambling [Owe95]

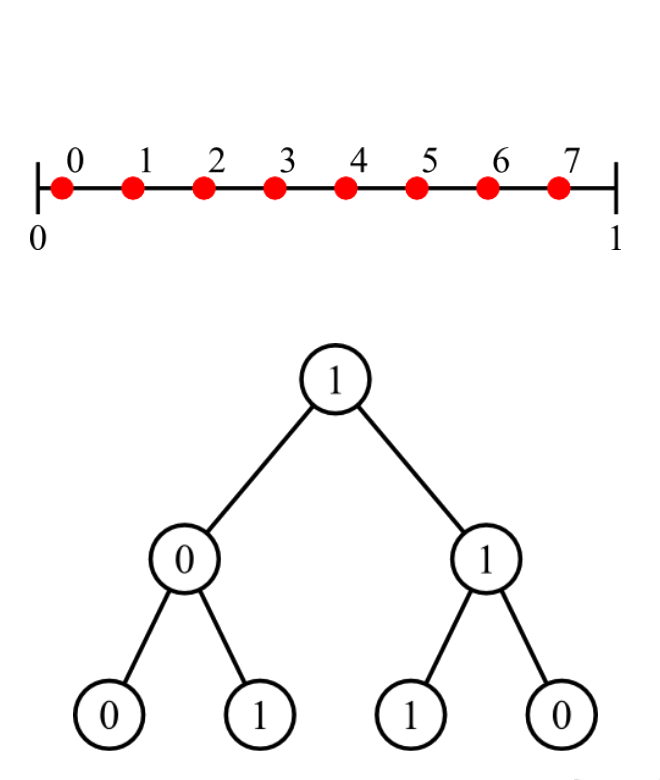
Owen's scrambling [Owe95]

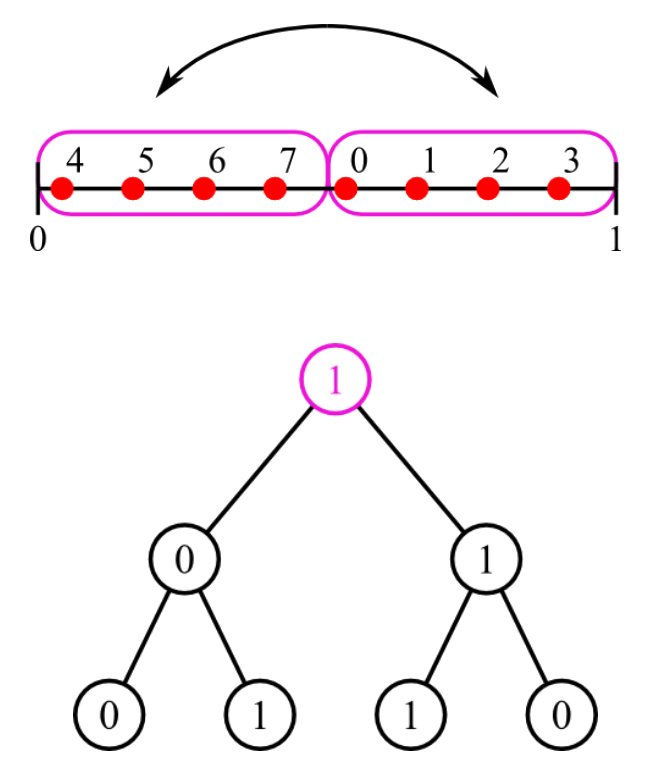
Owen's scrambling [Owe95]

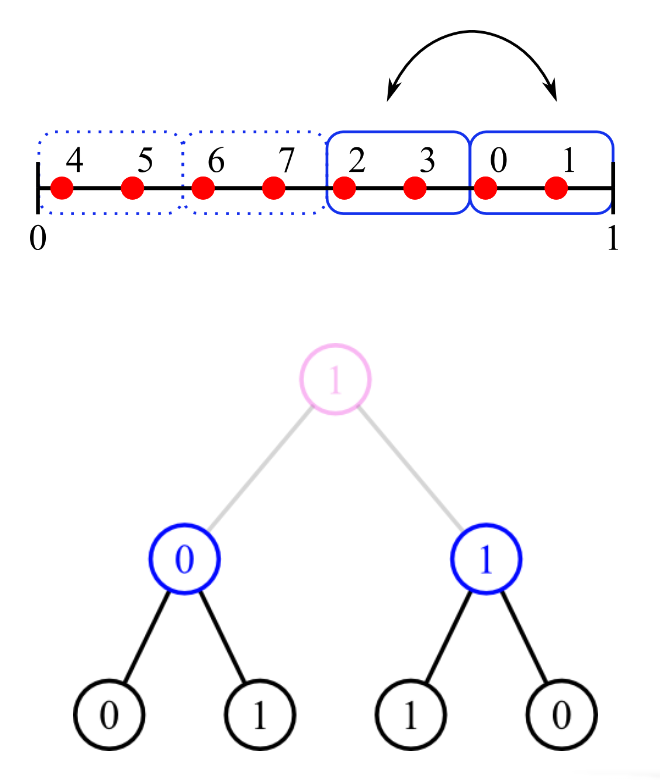
Owen's scrambling [Owe95]

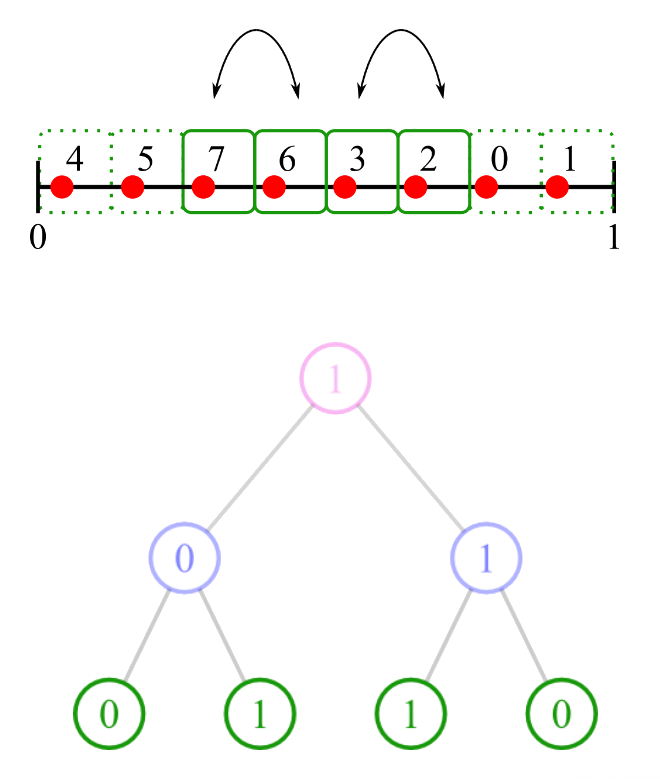
Owen's scrambling [Owe95]

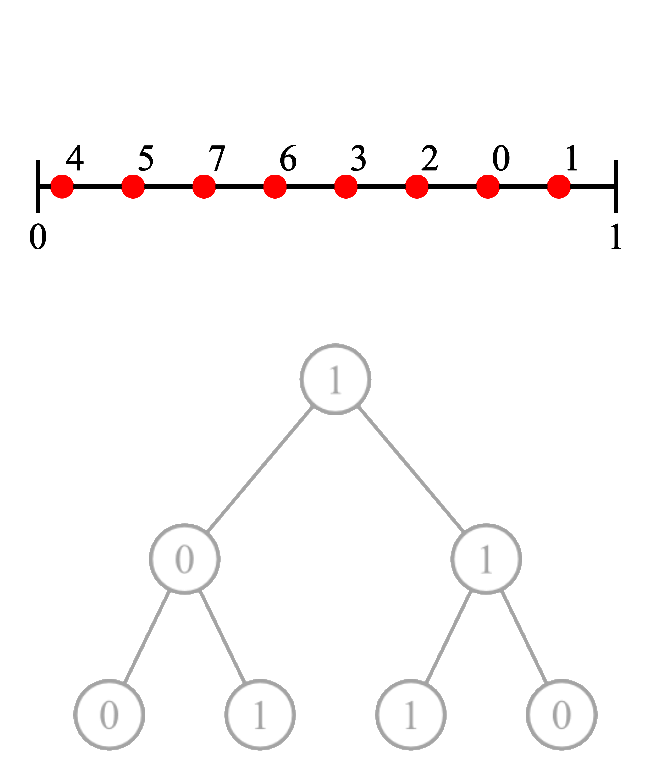
Owen's scrambling [Owe95]







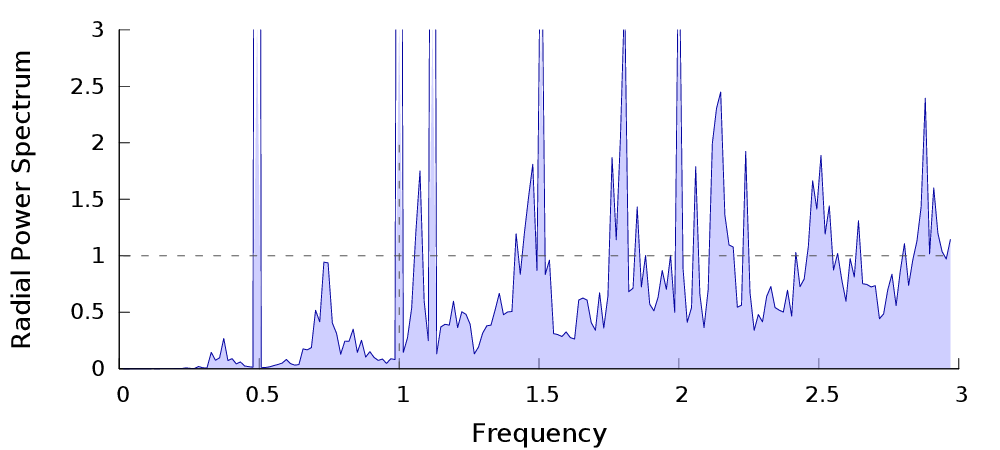
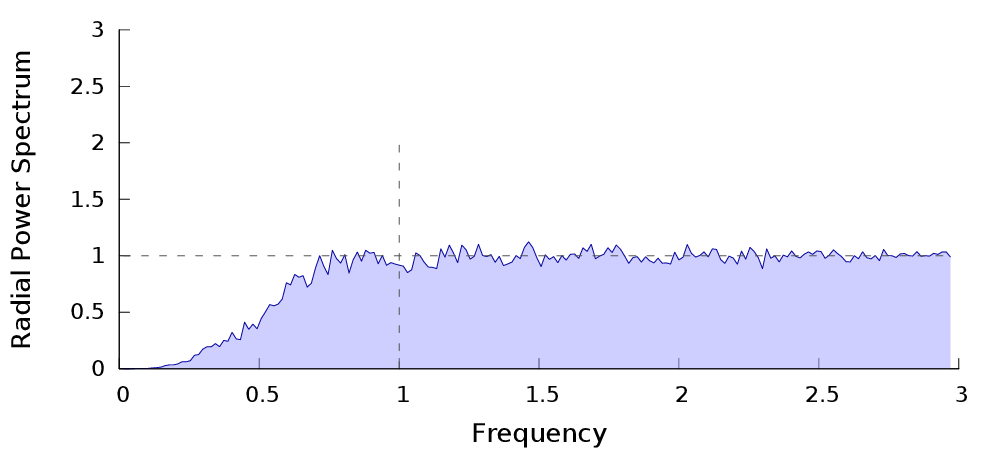
Niveau 1, 2-D, $K=4$

On génère $K^d=16$ points à partir de Sobol. On note cet ensemble $\mathcal{S_0}$.

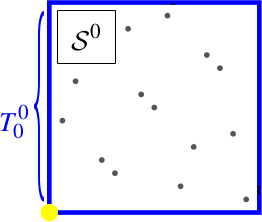
Et on les mélange en utilisant un Owen scrambling pour leur donner un spectre bruit bleu. On note le nouvel ensemble $\mathcal{P_0}$.

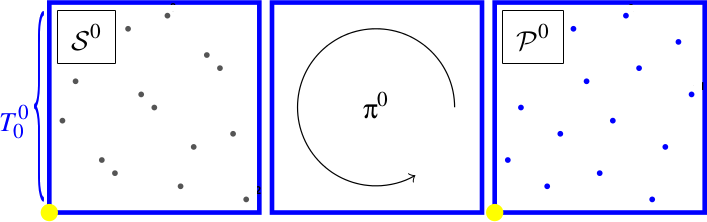
Niveau 2, 2-D, $K=4$

On génère $K^{2d}=256$ points à partir de Sobol. On note cet ensemble $\mathcal{S_1}$.

On commence par appliquer un scrambling global sur cet ensemble pour reconstruire $\mathcal{P_0}$. On note le nouvel ensemble $\mathcal{Q_1}$.

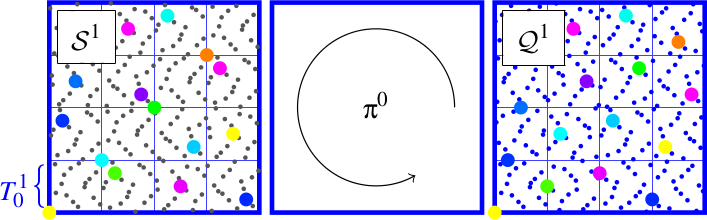
Niveau 2, 2-D, $K=4$

Ensuite, on scramble les points dans chaque tuile $\mathcal{T_1^{i}}$ de $\mathcal{Q_1}$ pour obtenir un spectre globalement bruit bleu.

Et ainsi de suite ...

Garanties

Quand $d = 2$, si $\mathcal{Q}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$, $\mathcal{P}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$

Si l'ensemble initial est dyadique en base $K$ (et donc est basse discrépance), notre ensemble de permutations locales préserve la dyadicité de cet ensemble (et donc la basse discrépance).

Garanties

Quand $d = 2$, si $\mathcal{Q}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$, $\mathcal{P}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$

Si l'ensemble initial est dyadique en base $K$ (et donc est basse discrépance), notre ensemble de permutations locales préserve la dyadicité de cet ensemble (et donc la basse discrépance).

Quand $d = 2$, si $\mathcal{S}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$, $\mathcal{Q}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$

Si l'ensemble initial est dyadique en base $K$ (et donc est basse discrépance), notre permutation globale préserve la dyadicité de cet ensemble (et donc la basse discrépance).

Garanties

Quand $d = 2$, si $\mathcal{S}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$, $\mathcal{P}^\lambda$ est un $(t, \lambda+1, 2)$-net en base $K$

Si l'ensemble initial est dyadique en base $K$ (et donc est basse discrépance), notre permutation préserve la dyadicité de l'ensemble (et donc la basse discrépance).

Pipeline final

n-D

n-D obtenu par scrambling indépendant de projections 2D.

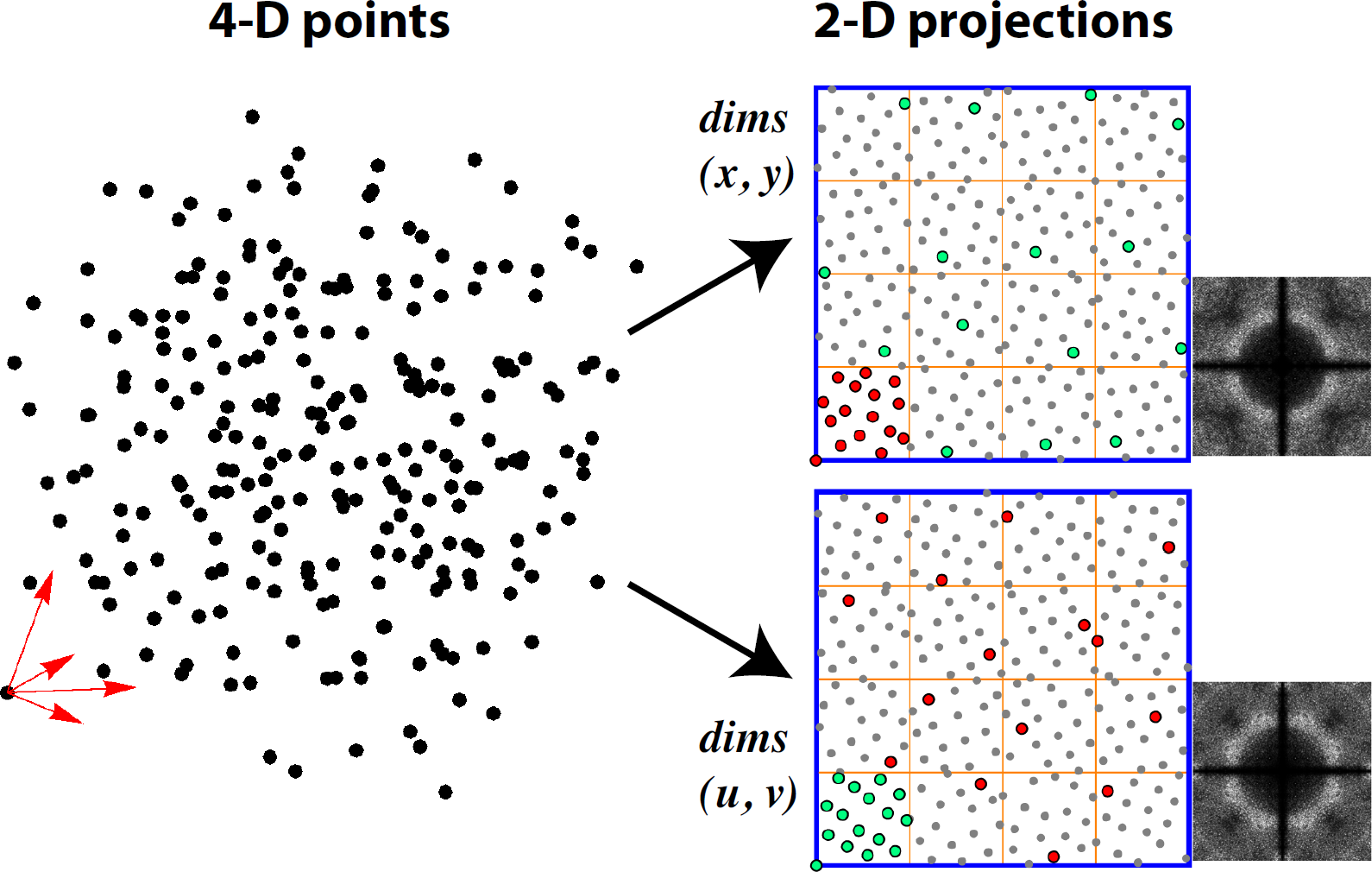
Adaptative sampling

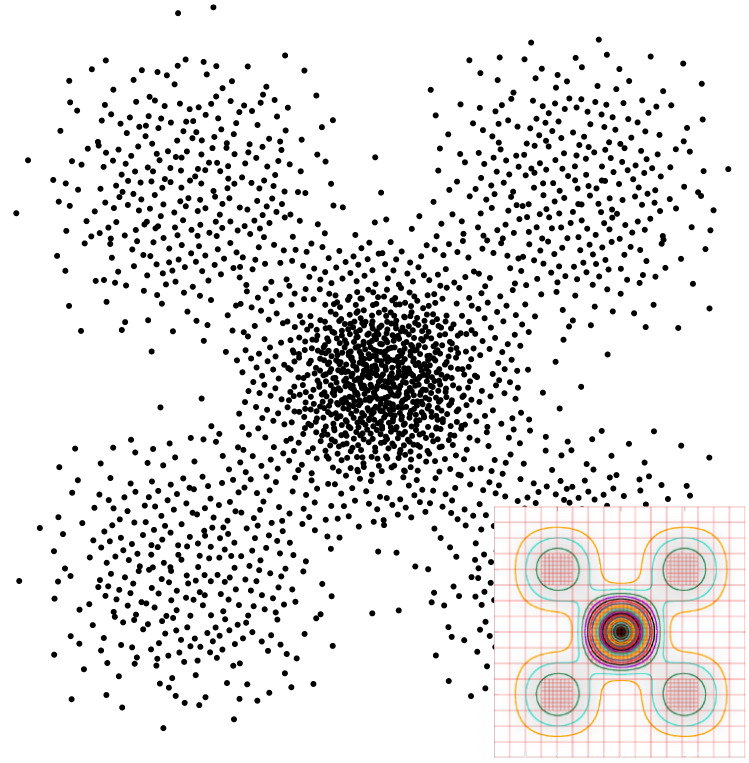
Results

BNOT [GBO+12] Owen's Scrambling [Owe95]
LDBN MultiProj

Results

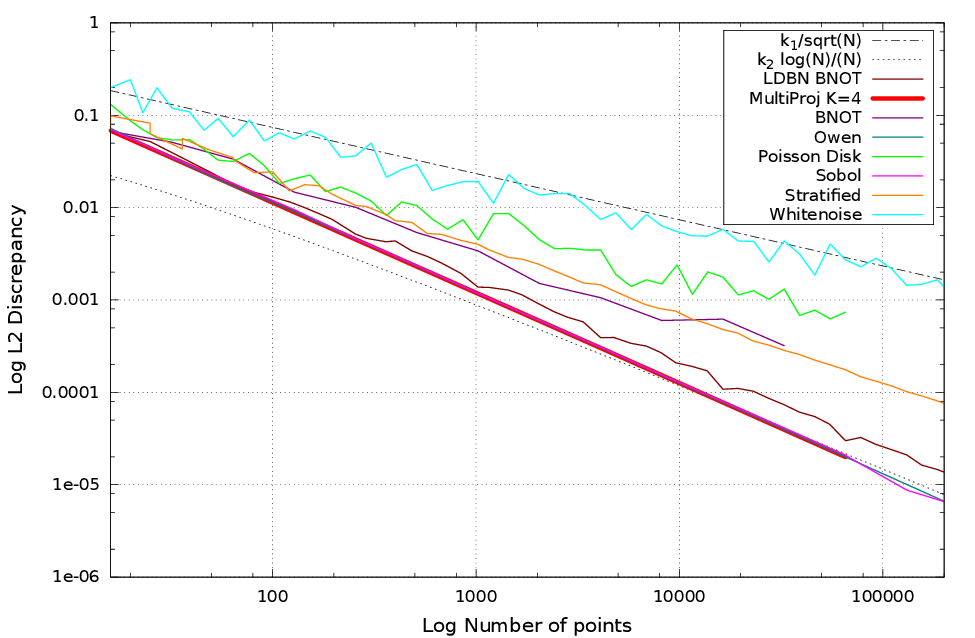
Results

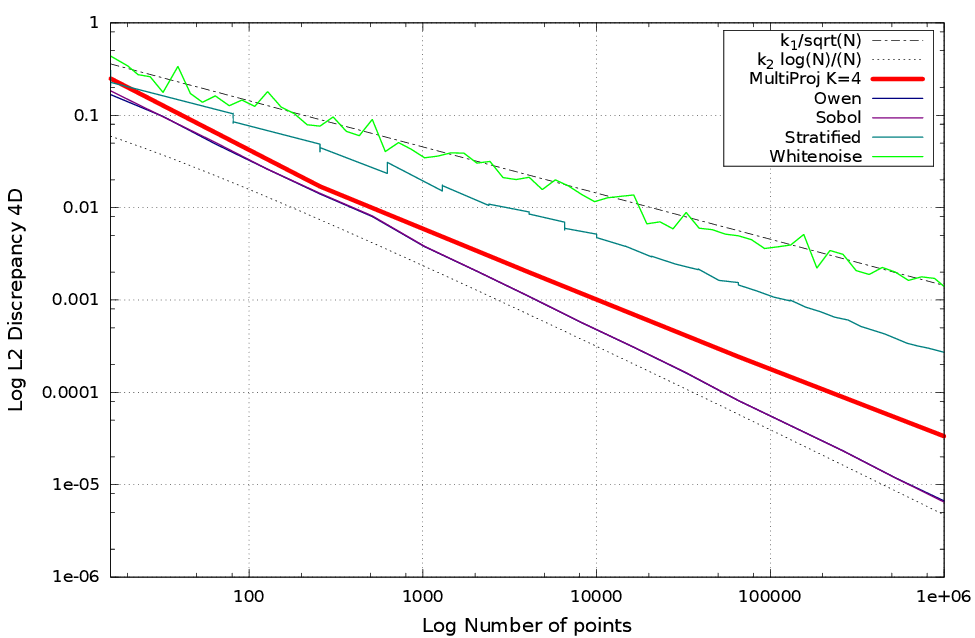
Results

Results

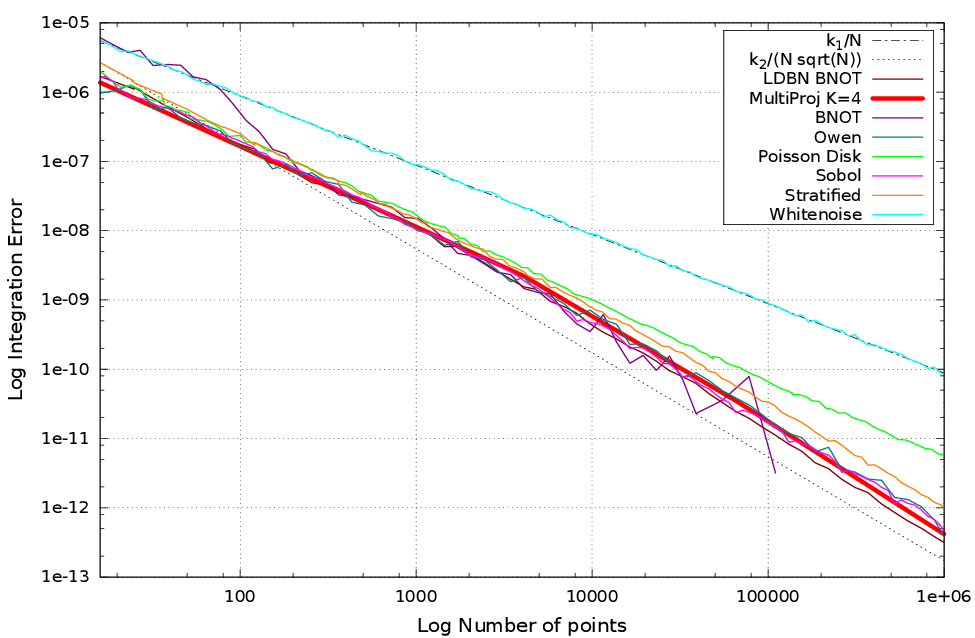
Results

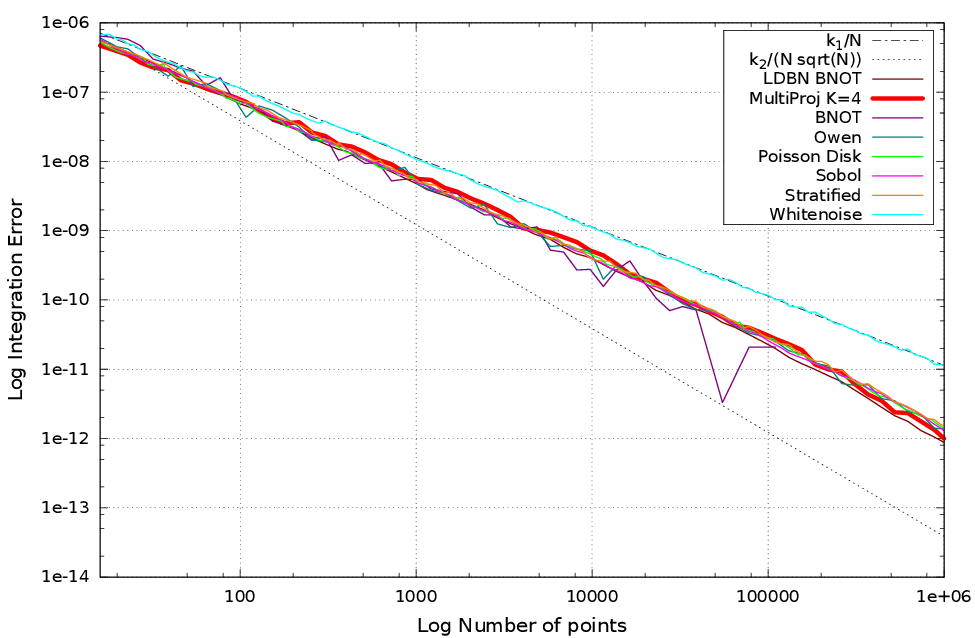
Results

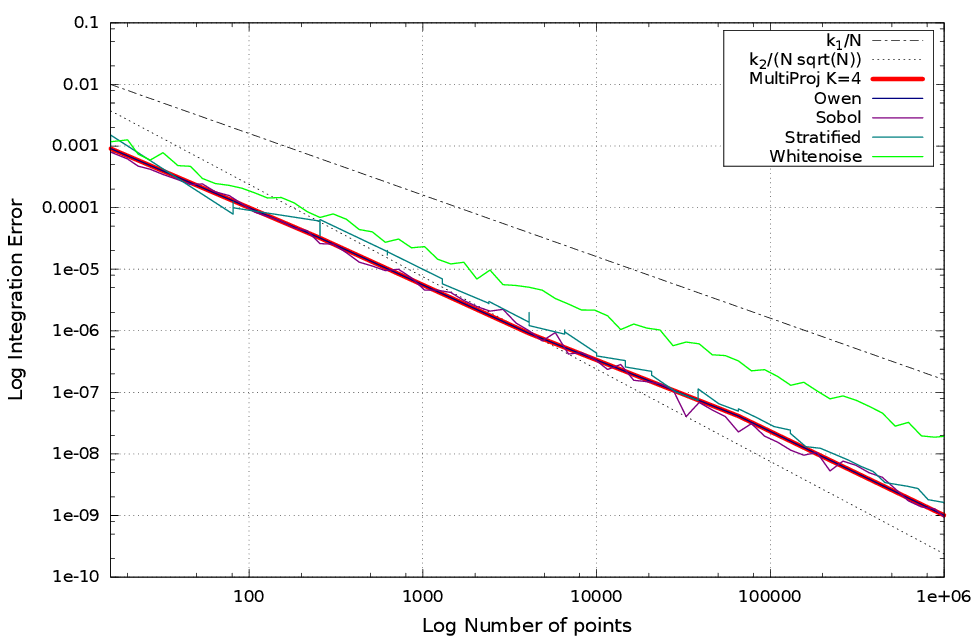
n-D

En fonction de $K$ on peut optimiser un certain nombre de dimensions.

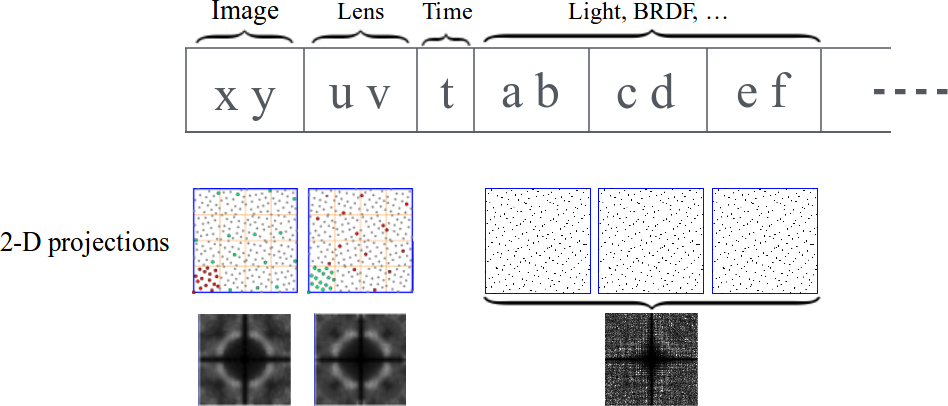
Results


Echantillons 4-D, 16 samples per pixel.
Stratified (MSE:0.0022) Sobol [Sob67] (MSE:0.0018) Owen's Scrambling [Owe95] (MSE:0.0017) MultiProj K=8 (MSE:0.0018)

Results


Echantillons 10-D, 16 samples per pixel.
Stratified (MSE:0.0017) Sobol [Sob67] (MSE:0.0015) Owen's Scrambling [Owe95] (MSE:0.0016) MultiProj K=8 (MSE:0.0013)

  • n-D
  • Fast, adaptive
  • Blue Noise Discribution for pairs of dimensions
  • Sequence
  • Low discrepancy in 2D projections only
  • Good discrepancy in nD



  • Tradeoff between being Low Discrepancy and Spectrum quality
  • Still have some permutations to precompute offline

Sliced Optimal Transport Sampling

Advanced topics

Sampling non-uniform densities

General idea

Objective: sample a 2D joint density function $p(x,y)$

Compute marginal density: $$p(x) = \int p(x,y)dy$$ Conditional density function: $$p(y|x)=\frac{p(x,y)}{p(x)}$$ Idea: estimate the marginal in one direction, sample $y$ according to this 1D marginal pdf

Options:

  • compute an area-preserving parametrization of $p(x,y)$
  • compute the analytical marginals when possible
  • estimate them using tabulated approaches

Example: sampling of a triangle

  $\Rightarrow$  

$$ s = (1-\sqrt{u_1}) A + u_2\sqrt{u_1} B + \sqrt{u_1}(1-u_2) C$$
with $u_1$, $u_2$ unform samples in $[0,1)$

Sampling non-square domains

Change of variables + unitary det of the Jacobian $\Rightarrow$ Area0 preserving mapping

Classical domains in rendering

$$x=cos(2\pi u_2)\sqrt{1-u_1^2}\\ y=sin(2\pi u_2)\sqrt{1-u_1^2}\\ z=u_1$$

But also

  • Disk
  • Cosine-weighted hemisphere
  • Cone
  • Camera ray
  • Piecewise-constant 2D distributions

Further reading

Metropolis, Markov chain,...

Sample $p(x)$ by just probing the function (no marginal nor integration)

Sketch of the algorithm:

  • Draw sample $x_0$ in $\Omega$
  • while I'm done
    • Compute the mutation of $x_i$ to construct $x'$
    • Evaluate the "acceptance" of $x'$, $a=accept(x_i,x')$
    • if $(U(0,1) < a)$ then $x_{i+1} = x' $
    • Record $x_{i+1}$

Key ingredients

  • Mutation strategy: $T(a\rightarrow b)$ the PDF to mutate $a$ to $b$ (e.g. random walk $b= (a+ \alpha u)$ mod 1, $u\in\mathcal{U}(0,1)$)
  • Acceptance strategy: $accept(x,x')= min\left(1,\frac{p(x')T(x'\rightarrow x)}{p(x)T(x\rightarrow x')}\right)$
  • + many tricks to avoid start-up bias
  • may converge to a sampling of $p(x)$

Bayesian approaches, Markov Chain Monte Carlo, density estimation...

Variance reduction tricks: Importance Sampling

Estimate $\int f(x)dx$ using $$ I_n= \frac{1}{n}\sum \frac{f(s_i)}{p(s_i)}$$ with a distribution $p(x)$ as close as possible to $f(x)$.

(weighting of the sample contributions w.r.t. estimate distribution $p$)

Ideal example: $p(x) := cf(x)$, then $Var(I_n)=0$

Importance sampling may increase the variance but there are many situations / technical ways to estimate $p(x)$ that improve the convergence

Variance reduction tricks: Multiple Importance Sampling

Estimate product of functions $\int f(x)g(x)dx$.

Questions:

  • same sampling strategy for both? e.g. $h(x):=f(x)g(x)$
  • Different strategies for $f$ and $g$ but how to weight them?

$$ I_n= \frac{1}{n_f}\sum_{n_f} \frac{f(s_i)g(s_i)w_f(s_i)}{p_f(s_i)} + \frac{1}{n_g}\sum_{n_g} \frac{f(s'_i)g(s'_i)w_g(s'_i)}{p_g(s'_i)}$$

For instance using the balance heuristic: $$ w_\bullet(x) := \frac{n_\bullet p_\bullet(x)}{\sum_i n_ip_i(x)} $$

or the power heuristic: $$ w_\bullet(x) := \frac{(n_\bullet p_\bullet(x))^\beta}{\sum_i (n_ip_i(x))\beta} $$




Variance reduction tricks: Control Variate

Instead of estimating $I=\int_\Omega f(x)dx$ using M.C., we estimate $$ I= \int_\Omega f(x) -\alpha h(x)dx + \alpha H$$ where $h(x)$ is the control variate
(and $H=\int_\Omega h(x)dx$ and $\alpha$ the strength of the control)

Then, $\langle I^*_n\rangle=\langle I_n - \alpha H\rangle + \alpha H$
choosing an optimal coefficient $\alpha=Cov(\langle I_n\rangle,\langle H_n\rangle) / Var(H_n)$,
we have
$$Var( I^*_n) = Var( I_n) (1 - Corr(\langle I_n\rangle,\langle H_n\rangle)^2)$$

Example:

  • $ I=\int_0^1 f(x)dx$, with $f(x)=\frac{1}{1+x}$
  • $ I_n= \frac{1}{n}\sum f(s_i)$,
  • sample $g(x)=1+x$ with $\int_0^1 g(x)dx=\frac{3}{2}$
  • $I_n = \frac{1}{n} \sum f(s_i) + c g(s_i) - c\frac{3}{2}$

$n=1500$, variance reduction from 0.01947 to 0.0006