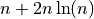Computational Geometry: Basic structures, Convex Hulls and Randomized Algorithms§
| author: | David Coeurjolly |
|---|
| author: | David Coeurjolly |
|---|
Objects
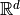
Geometrical problems
Theoretical questions
Idea
Example
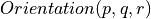 |
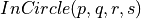 |
Cross product
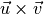 ‘norm’ is the signed area of the parallelogram
‘norm’ is the signed area of the parallelogram 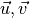 . Obviously,
. Obviously, 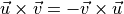
Orientation predicate = sign of the determinant
 {+, 0, - } output
{+, 0, - } output
Sometimes, Orientation is defined as the sign of the determinant of the following matrix
Problem
Given 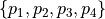 , decide if
, decide if ![[p_1p_2]](_images/math/358a10463d2de93a572c52aa8eb9f555f4ae8605.png) intersects
intersects ![[p_3p_4]](_images/math/bb354ab7190a0c55bc153fbd5ca8b5eb603700ce.png)
Algorithm
Simple reject case: if bounding box of ![[p_1p_2]](_images/math/358a10463d2de93a572c52aa8eb9f555f4ae8605.png) does not intersect the bounding box of
does not intersect the bounding box of ![[p_3p_4]](_images/math/bb354ab7190a0c55bc153fbd5ca8b5eb603700ce.png)
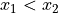 on point coordinates
on point coordinatesSegments intersects if each segment intersects the straight line defined by the other one
![[p_1p_2]](_images/math/358a10463d2de93a572c52aa8eb9f555f4ae8605.png) intersects
intersects 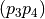 iff
iff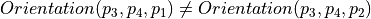
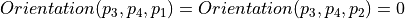 (aligned segments)
(aligned segments)Orientation predicate implementation
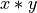 must be representable), exact computations for integer built-in types (int, long int, …)
must be representable), exact computations for integer built-in types (int, long int, …) uncertainty
uncertainty<CF Robustness CGAL>
 Error control, filtered predicates, formal rewritting, interval computations …
Error control, filtered predicates, formal rewritting, interval computations …
Step 1
Given a set of point  in
in 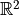 ,
,
Implementation
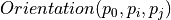 induces an polar order on points
induces an polar order on points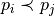
Step 1 is in 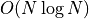
Step 2
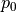 is necessarily a point in the convex hull (we assume
is necessarily a point in the convex hull (we assume 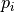 are sorted)
are sorted)Algo
Push(p0) to S
Push(p1) to S
Push(p2) to S
For i from 3 to N
While the angle (head(S / {head(S)}) , head(S), p_i) is convex
Pop(S);
Push(p_i) to S;
Step 2 is in 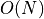
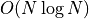 algorithm
algorithmIdea Recursive approach with decimation principle
function QuickHull(Set S, Point pLeft, Point pRight)
{
if S == {pLeft, pRight} return edge [pLeft,pRight]
pH = FurthestPoint(S, pLeft, pRight)
S1 = points of S on the left of vector [pLeft,pH]
S2 = points of S on the right of vector [pH,pRight]
return QuickHull(S1,pLeft,pH) + QuickHull(S2,pH,pRight)
}
//starting from two points on the convex hull (details skipped but not tricks here)
QuickHull is in 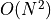 (but really fast)
(but really fast)
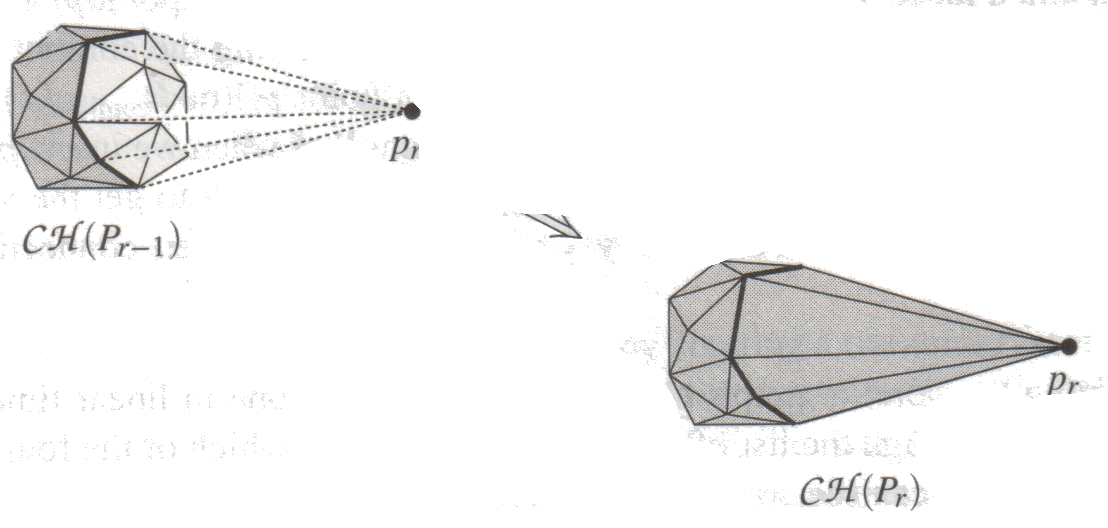
Problem we want to update CH(S + {p}) from CH(S)
|
|
Supporting lines can be extracted in 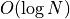 with Orientation predicate
with Orientation predicate
 incremental convex hull in
incremental convex hull in 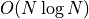
Problem Decide if a straight line intersect a convex polygon
<Cf board>
Problem settings Let 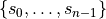 be a simple polygonal chain (no self-intersection)
be a simple polygonal chain (no self-intersection)
Solution Melkman’s algorithm
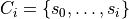 and
and 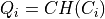
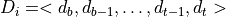 stores the sequence of points in
stores the sequence of points in 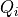 (with
(with 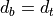 )
)
//Init
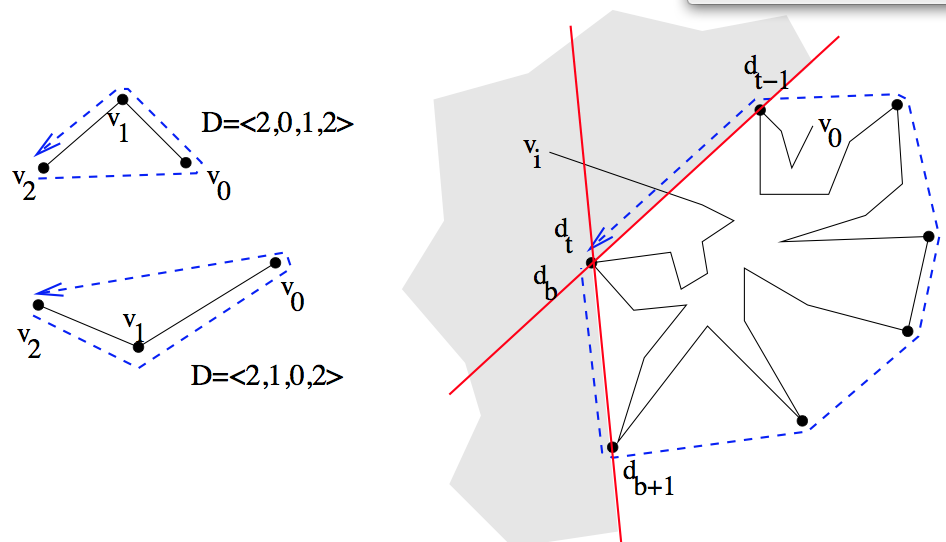
if Orientation(v0,v1,v2) then D=<v2,v0,v1,v2> else D=<v2,v1,v0,v2>
i = 3;
while (i<N)
{
//Simple case, no update required
while (Orientation(d_{t-1},d_t,vi)) and Orientation(d_b,d_{b+1}, vi))
i++;
//Ok, vi is exterior to Q_i, we restore the convexity
repeat
pop(d_t)
until Orientation(d_{t-1},d_t,vi);
push(vi);
repeat
remove(d_b)
until Orientation(vi,d_b,d_{b+1});
insert(vi);
}
//Done
Thanks to the simplicity of the polygonal chain, correctness can be demonstrated with  complexity
complexity
Given a set S pf N points in space
Dimension 2 CH(S) has O(N) vertices/edges
Dimension 3
any convex polytope with n vertices has
(proof: convex polytope  planar graph
planar graph 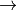 Euler’s formula
Euler’s formula 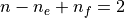 and
and 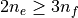 )
)
 complexity of CH(S) in 3-space is O(N)
complexity of CH(S) in 3-space is O(N)
Dimension d
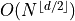
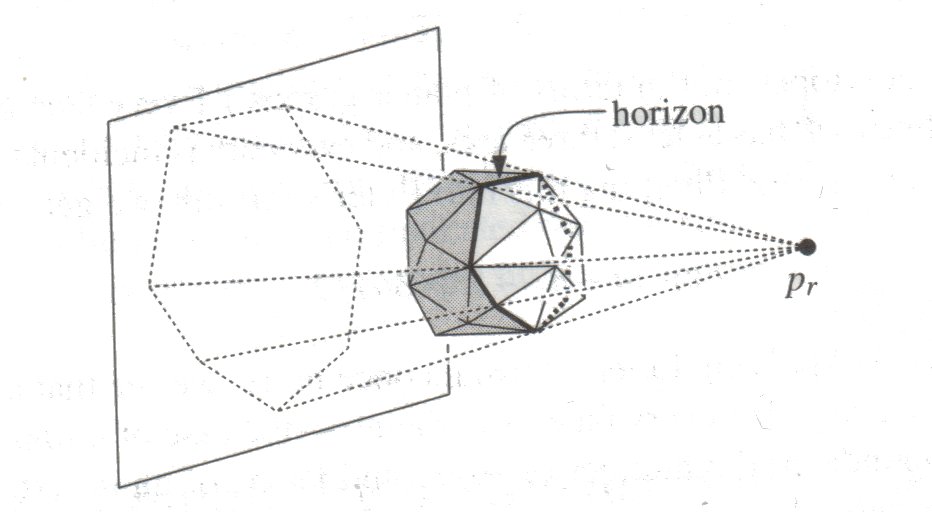
Visibility based approaches
Extract visibility horizon and update the convex hull
|
|
Idea
Computational cost proportional to the output size.
Dim 2
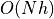
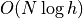
Dim 3
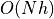
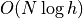
Dim d
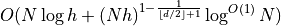
Simple construction
Idea
For some algorithms, randomized algorithm can be defined with expected computational cost
E.g. “the expected computational cost of algorithm A is O(N)”
Keep in mind that
Why?
Idea
Given a set of segments 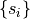 , we construct a binary tree partitioning the space such that each segment splits the space by its associated line
, we construct a binary tree partitioning the space such that each segment splits the space by its associated line 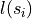
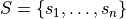
function 2DBSP(S)
{
if (Card(S) <= 1)
Create a tree T consisting of a single leaf node containing S
else
{
//We split along l(s1) (first element of S)
S+ = { s\cap l(s1)+, s in S);
S- = { s\cap l(s1)-, s in S);
T+ = 2DBSP(S+)
T- = 2DBSP(S-)
Create a tree T with root node v (S(v)={s in S, s subset l(s1)})
and sub-trees T+ and T-
}
return T;
}
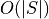 new segments (called fragments)
new segments (called fragments)function Random2DBSP(S)
{
Generate random permutation S'=s1, ..., sn of the set S
return 2DBSP(S')
}
Nice, but does it help to bound the number of fragments ?
Main result
Thm.
The expected number of fragments generated by Random2DBSP is 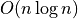
(instead of 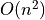 with naive approach)
with naive approach)
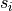
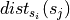 the number of segments intersecting
the number of segments intersecting 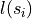 in between
in between 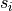 and
and 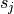
(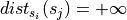 if
if 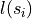 does not intersect
does not intersect 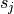 )
)
Let us define 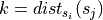 and let
and let 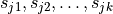 be such segments between
be such segments between 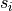 and
and 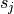 .
.
Question what is the probability that 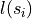 cut
cut 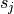 ?
?
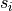 must be before
must be before 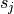 is the random sequence. Moreover,
is the random sequence. Moreover, 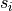 must be before all segments
must be before all segments 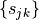
By uniformity hypothesis on the random permutation
Some segments 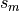 may exist such that
may exist such that 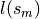 shield
shield 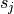 from
from 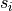 . Hence, we do not have an equality in the Expectation expression:
. Hence, we do not have an equality in the Expectation expression:
 By linearity of expectation, the expected number of segments is
By linearity of expectation, the expected number of segments is