Computational Geometry: Spatial Data Structures, Voronoi Diagram and Delaunay Triangulation§
| author: | David Coeurjolly |
|---|
| author: | David Coeurjolly |
|---|
Problem setting
Dimension 1
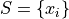
![[l,r]](_images/math/0c22d761d4ce4969404ed8545cd118deff48cb8b.png) , returns
, returns 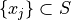 with
with ![x_j\in[l,r]](_images/math/f89b51e9658c6e4e8177cc7dd5c1e233bbd5cbf1.png)

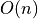 storage and
storage and 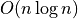 construction time, then
construction time, then 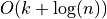 per query (
per query (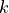 is number of reported points)
is number of reported points)
Idea
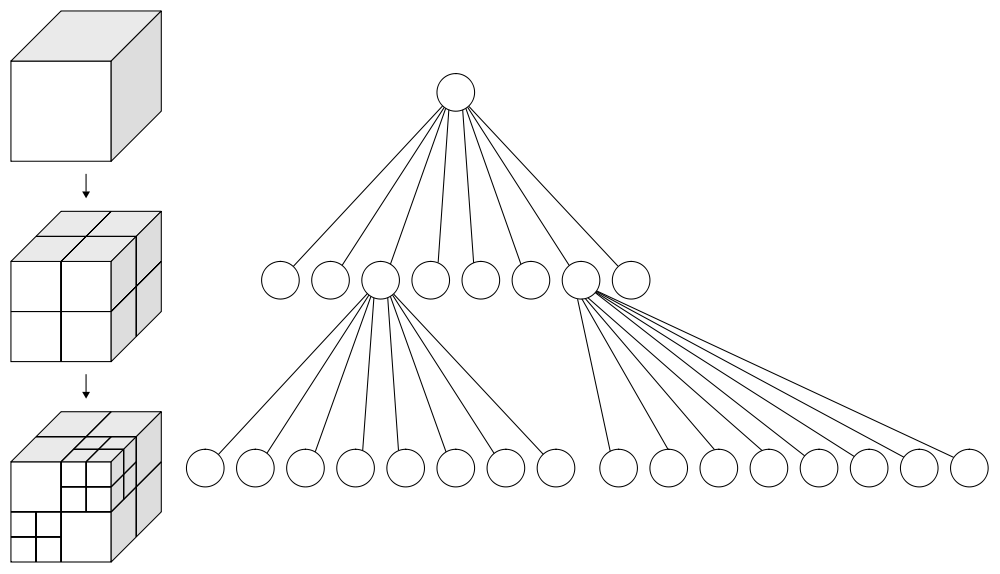
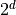 -ary tree
-ary tree depth depending in the min distance between two points
depth depending in the min distance between two points could be unbalanced
could be unbalanced fast bottom-up/top-down construction algorithms
fast bottom-up/top-down construction algorithms
|
|
Idea
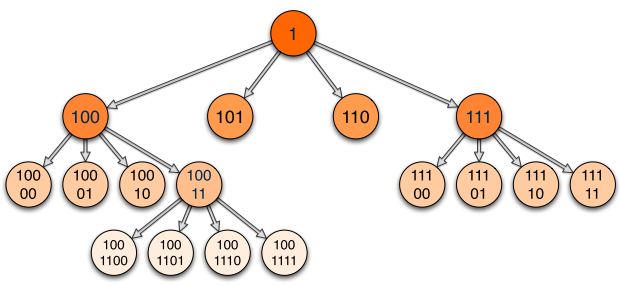
 Binary encoding (Morton codes) and implicit hierarchical structure
Binary encoding (Morton codes) and implicit hierarchical structure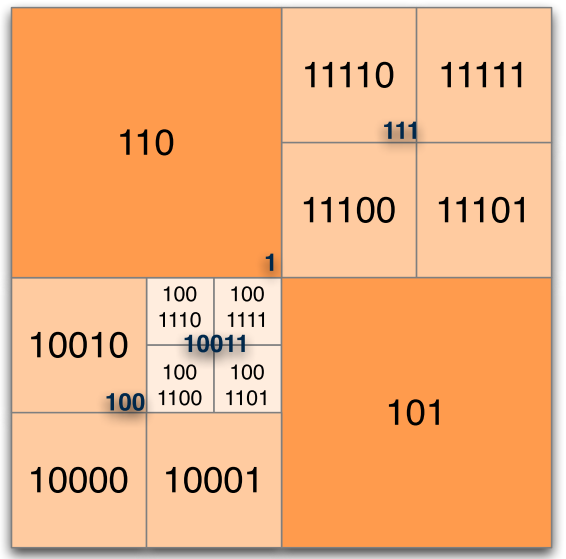
|
|
Ctd.
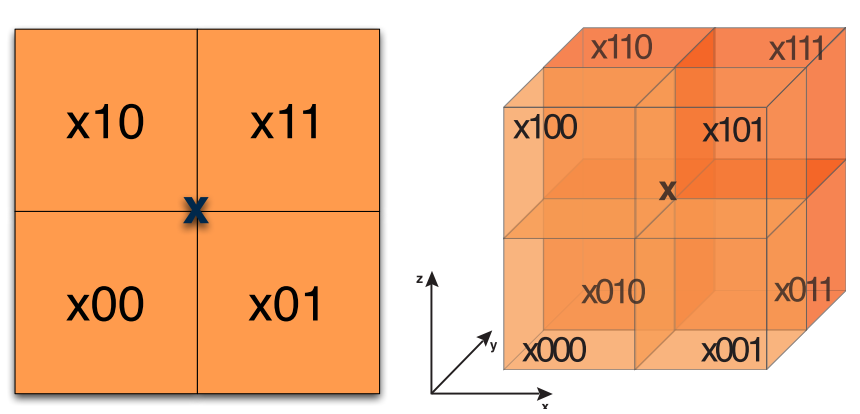
At construction, when we increase the depths, we just add 2 bits (2D) or 3 bits (3D) suffixes
One datum = one binary code
Localizing a point = bit code interleaving on binary representation of point coordinates
Final encoding: hash map on binary morton codes
… but
Description
Pseudo-code in 2D:
BuildKdTree(S, depth)
if |S|=1
return a leaf containing this point
if depth is even
Let l be the vertical line with median x-coordinate
Split S w.r.t. l -> S1 and S2
if depth is odd
Let l be the horizontal line with median y-coordinate
Split S w.r.t. l -> S1 and S2
SubTree1 = BuildKdTree(S1,depth + 1)
SubTree2 = BuildKdTree(S2,depth + 1)
return Tree(l , SubTree1, SubTree2)
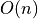
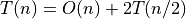
 KdTree construction in
KdTree construction in 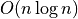 ,
, 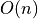 storage
storage
Example <Cf board>
Random algorithm
QuickSelect(A, k)
Pick a pivot element p randomly from A
Split A into LESS and GREATER sets
L = number of elements in the LESS array
if (L == k-1)
return p;
if (L > k-1)
return QuickSelect(LESS, k)
if (L < k-1)
return QuickSelect(GREATER, k - L - 1)
 randomized O(n) expected time to get the k-rank element
randomized O(n) expected time to get the k-rank element
Deterministic algorithm
QuickSelect(A, k)
Group the array into n/5 groups of size 5
Find the median of each group //Let M be the set of medians
p = QuickSelect(M,k) // median of the medians
Split A into LESS and GREATER sets
L = number of elements in the LESS array
if (L == k-1)
return p;
if (L > k-1)
return QuickSelect(LESS, k)
if (L < k-1)
return QuickSelect(GREATER, k - L - 1)
 Deterministic O(n) time to get the k-rank element (details skipped but I encourage you to have a look!)
Deterministic O(n) time to get the k-rank element (details skipped but I encourage you to have a look!)
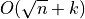
Algo
RangeQueryKdTree(node, Range)
//Stop
if node is a leaf
return the p point in node if p in Range
//left child
if region(leftChild(node)) is fully contained in Range
return all points in the subtree leftChild(node) //(A)
else
if region(leftChild(node)) intersects Range
return RangeQueryKdTree( leftChild(node) , Range)
//right child
if region(rightChild(node)) is fully contained in Range
return all points in the subtree rightChild(node) //(B)
else
if region(rightChild(node)) intersects Range
return RangeQueryKdTree( rightChild(node) , Range)
Hints
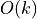
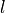 (left/right interval in Range)
(left/right interval in Range)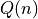 be the number of such regions in a kdTree with n vertex whose root is a vertical line
be the number of such regions in a kdTree with n vertex whose root is a vertical lineObs1 If 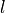 is vertical and the constraint of the root is vertical,
is vertical and the constraint of the root is vertical, 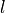 only crosses one of the root children regions
only crosses one of the root children regions
Obs2 If 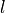 is vertical and the constraint of the root is horizontal,
is vertical and the constraint of the root is horizontal, 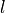 crosses both root children regions
crosses both root children regions
 two step recurrence (sub-trees of depth 2 have n/4 points)
two step recurrence (sub-trees of depth 2 have n/4 points)

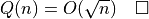
Thm.
Range tree structure in dimension d with 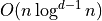 storage constructed in
storage constructed in 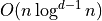 can answer to hyperrectangular range queries in
can answer to hyperrectangular range queries in 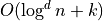 .
.
(Some images from Olivier Devillers, INRIA Sophia-Antipolis)
Setting Given a set of sites 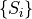 , answer to closest site queries
, answer to closest site queries
Setting Given a set of sites 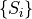 , answer to closest site queries
, answer to closest site queries
Setting Given a set of sites 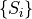 , answer to closest site queries
, answer to closest site queries
Setting Given a set of sites 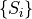 , answer to closest site queries
, answer to closest site queries
Setting Given a set of sites 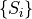 , answer to closest site queries
, answer to closest site queries
Find closest site <=> point location in a Voronoi diagram
Key Property for Delaunay triangle/edges Empty circle property
Remember the 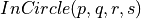 predicate ?
predicate ?
true if  lies inside the circumscribing circle of the triangle
lies inside the circumscribing circle of the triangle 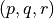
Triangulation where smallest angle is maximal
true for all angles in lexicographic order
Many deeper properties
Widely used for surface reconstruction and finite element computations for example
Local Delaunay tests
Given a triangle T(a,b,c) and adjacent triangles T(a,b,p), T2(a,c,q) and T3(b,c,r), T is locally delaunay if 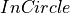 predicates (a,b,c,p) (a,b,c,q) and (a,b,c,r) fails
predicates (a,b,c,p) (a,b,c,q) and (a,b,c,r) fails
Main result
Thm.
Everywhere locally Delaunay 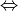 Globally Delaunay
Globally Delaunay
Naive Algorithm
Start from any valid triangulation
While there is an invalid triangle w.r.t. empty circle property, perform edge flipping
 the algorithm stops and produces a correct Delaunay triangulation
the algorithm stops and produces a correct Delaunay triangulation
Idea
SubProblems
returns the triangle T containing p
locally triangulate the one-ring of T + p
maintain Delaunay property
Straightforward analysis
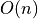
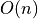

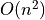
Main Idea
Localize the point using sequence of displacement in the triangulation
We are looking for better expected computational cost
Idea
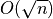 for uniform point distributions
for uniform point distributions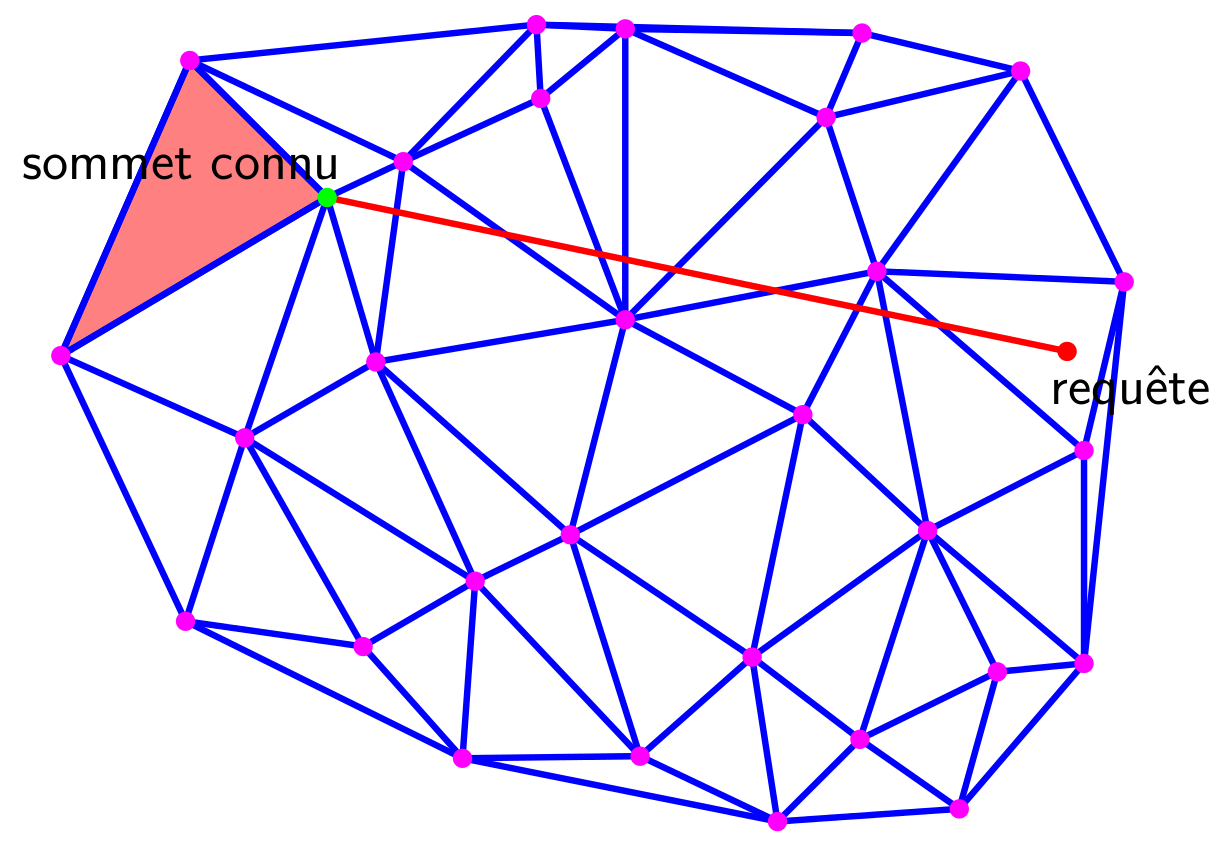
|

|
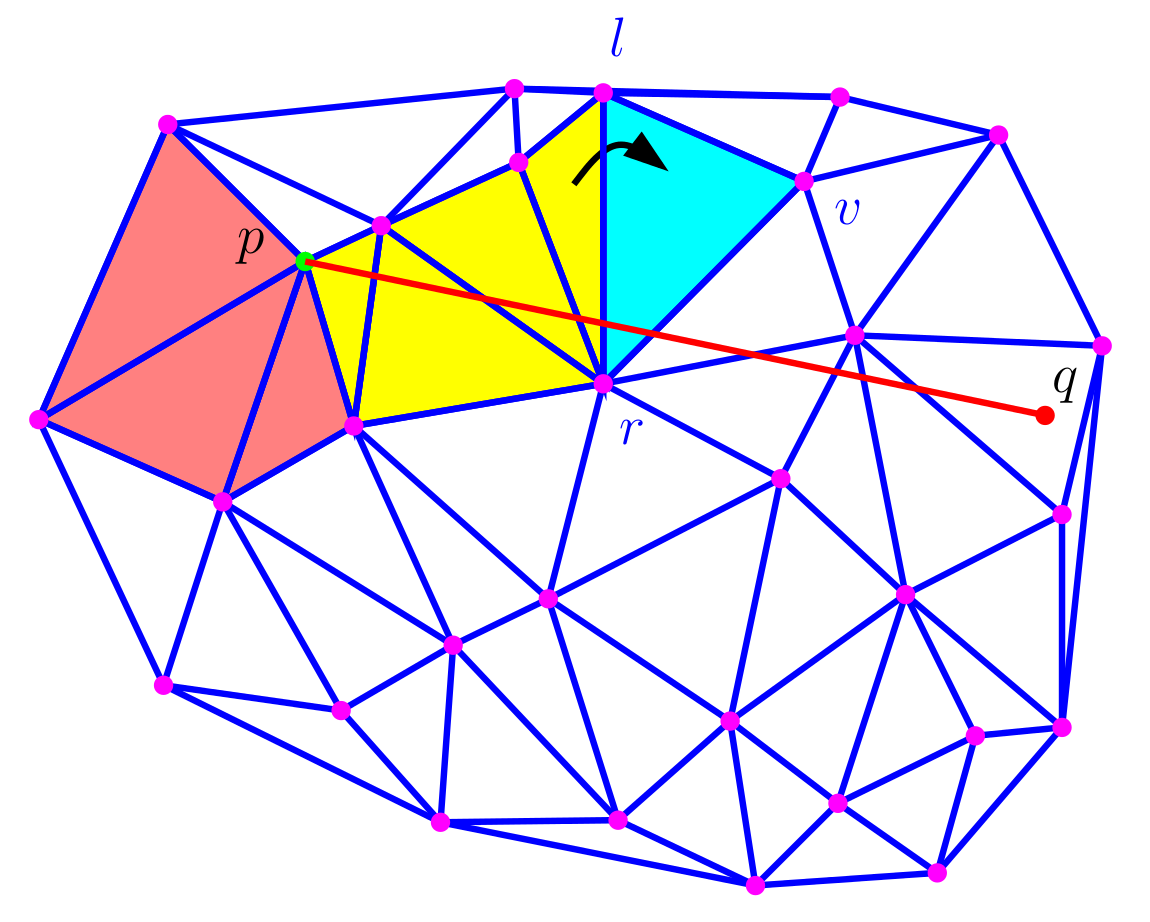
|
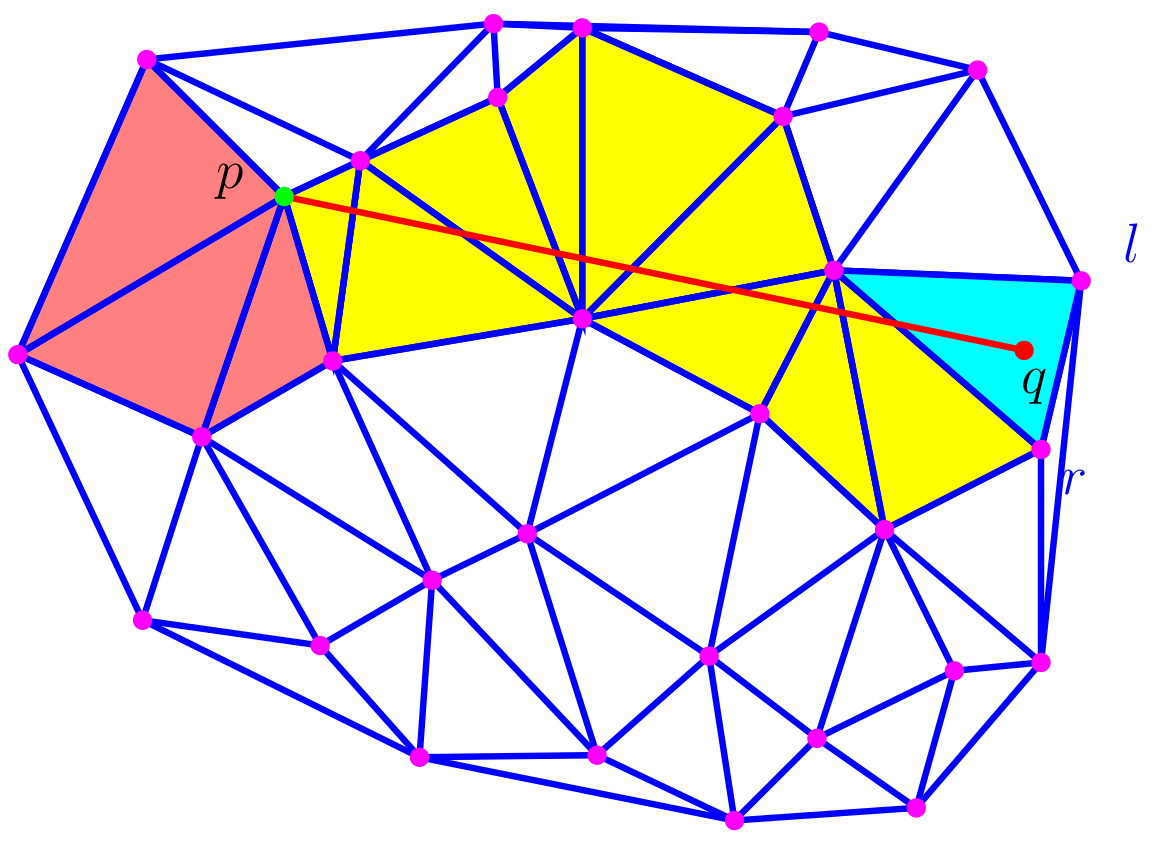
|
Important bad orientation predicates may lead to cycles in the walk…
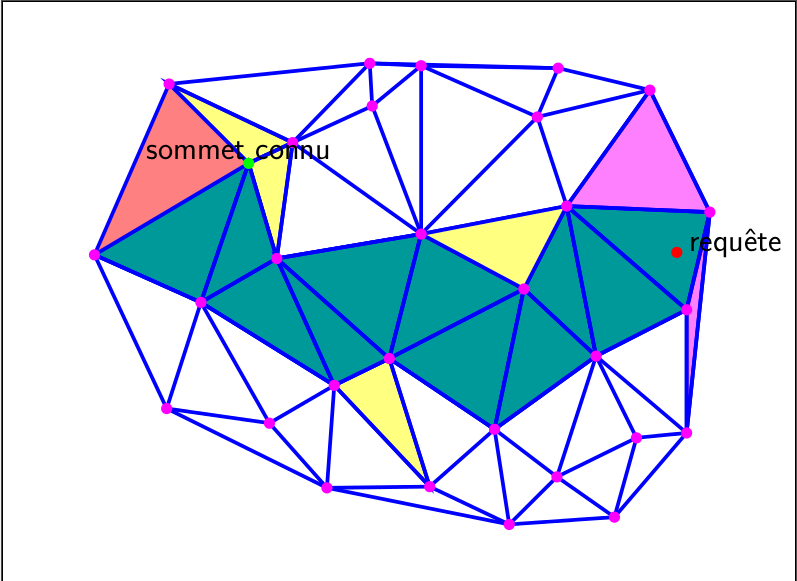
Visibility walk
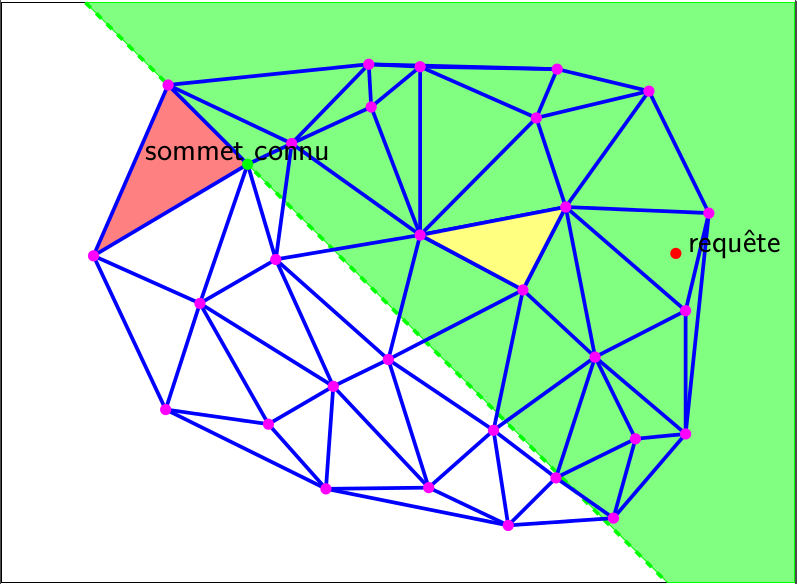
|
|
Jump & Walk
Hierarchical structure
…
Delaunay Triangulation can be obtained in 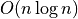 (
(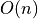 storage)
storage)
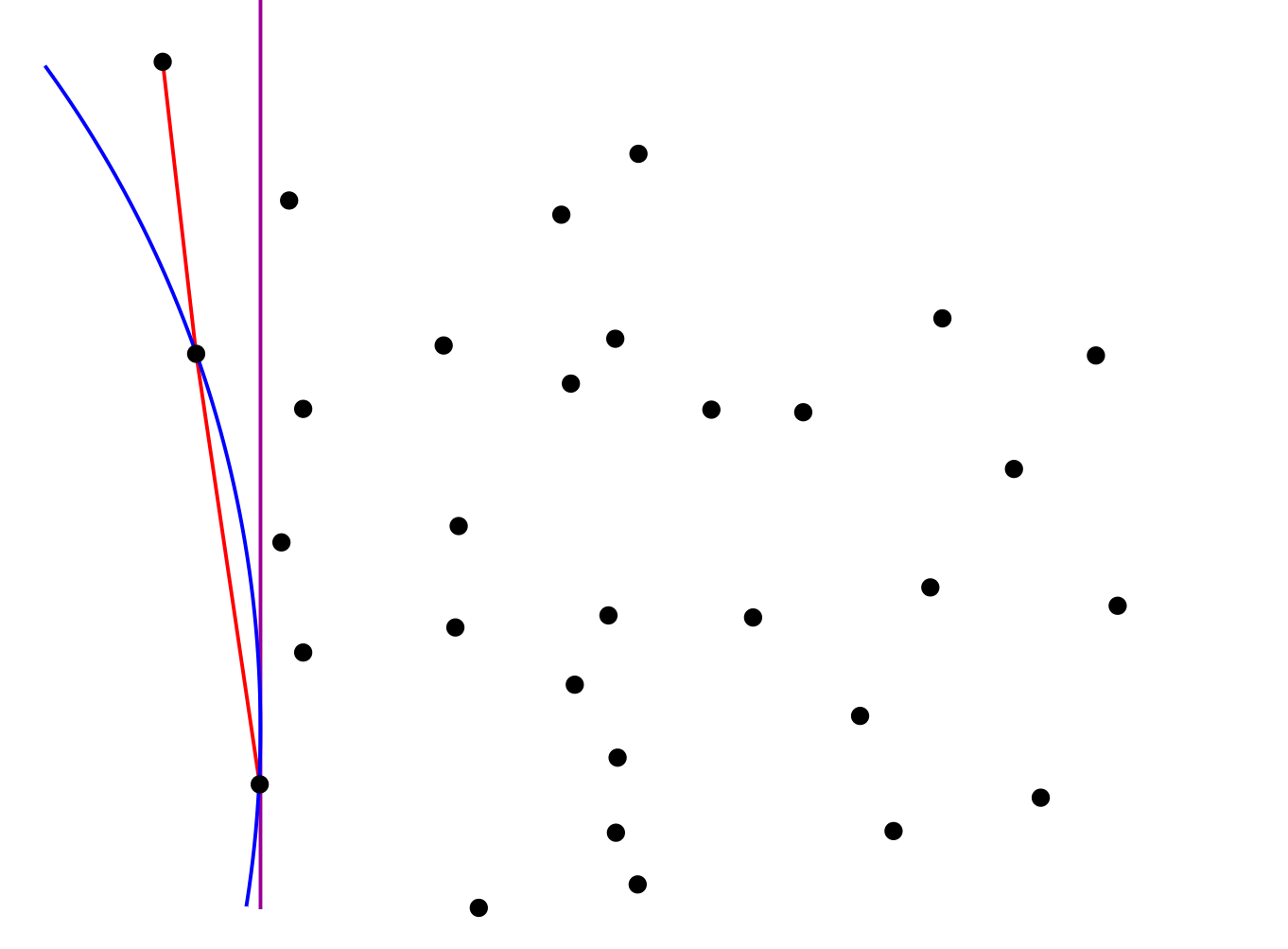
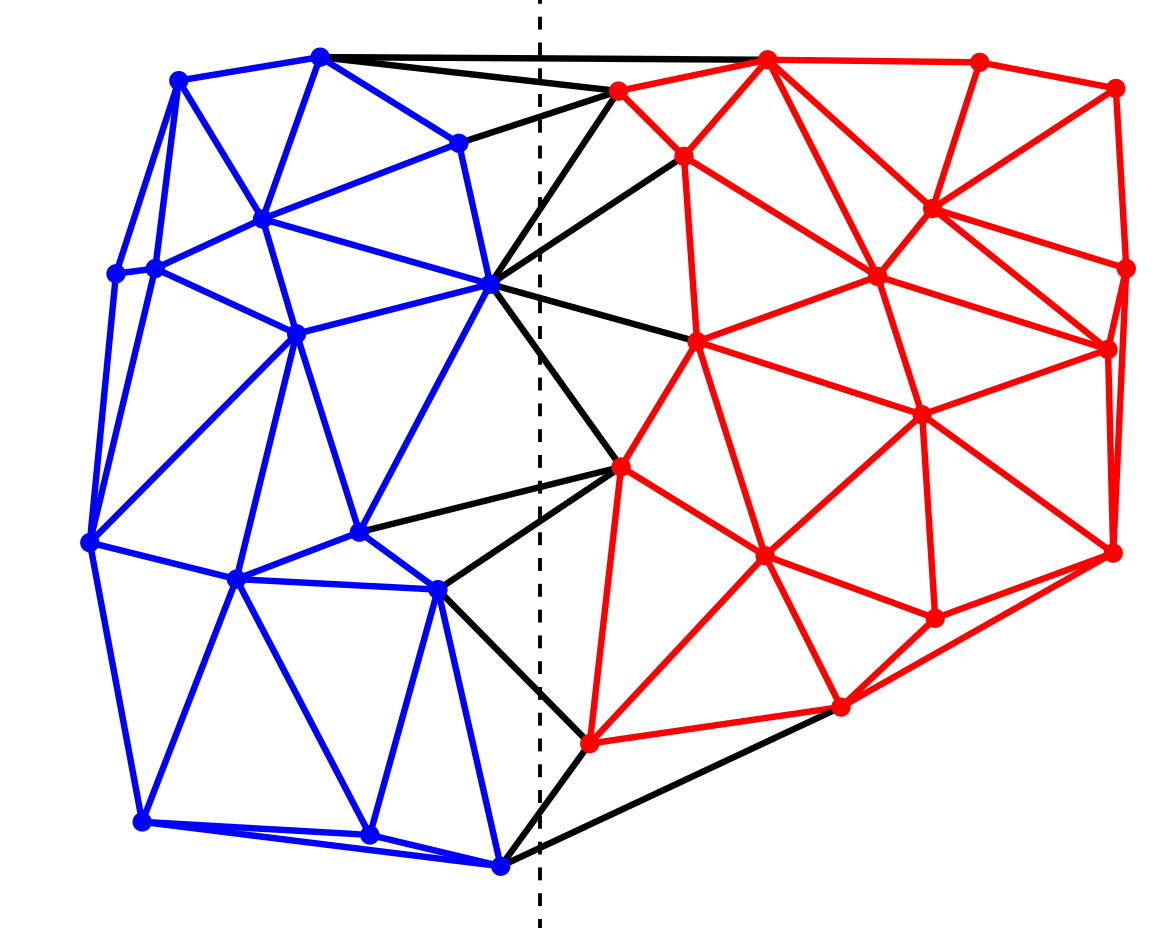
Idea

|
|
|
|
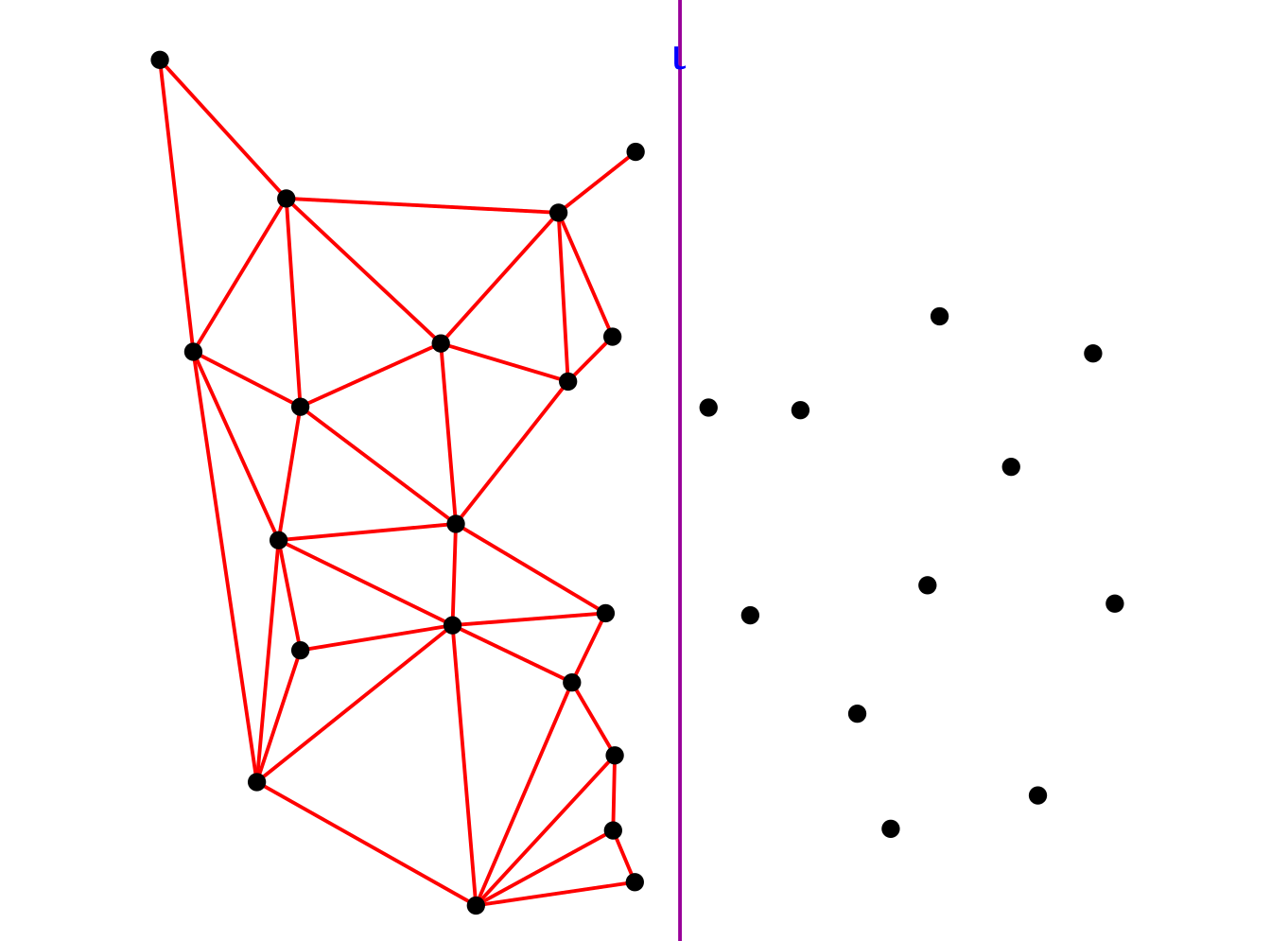
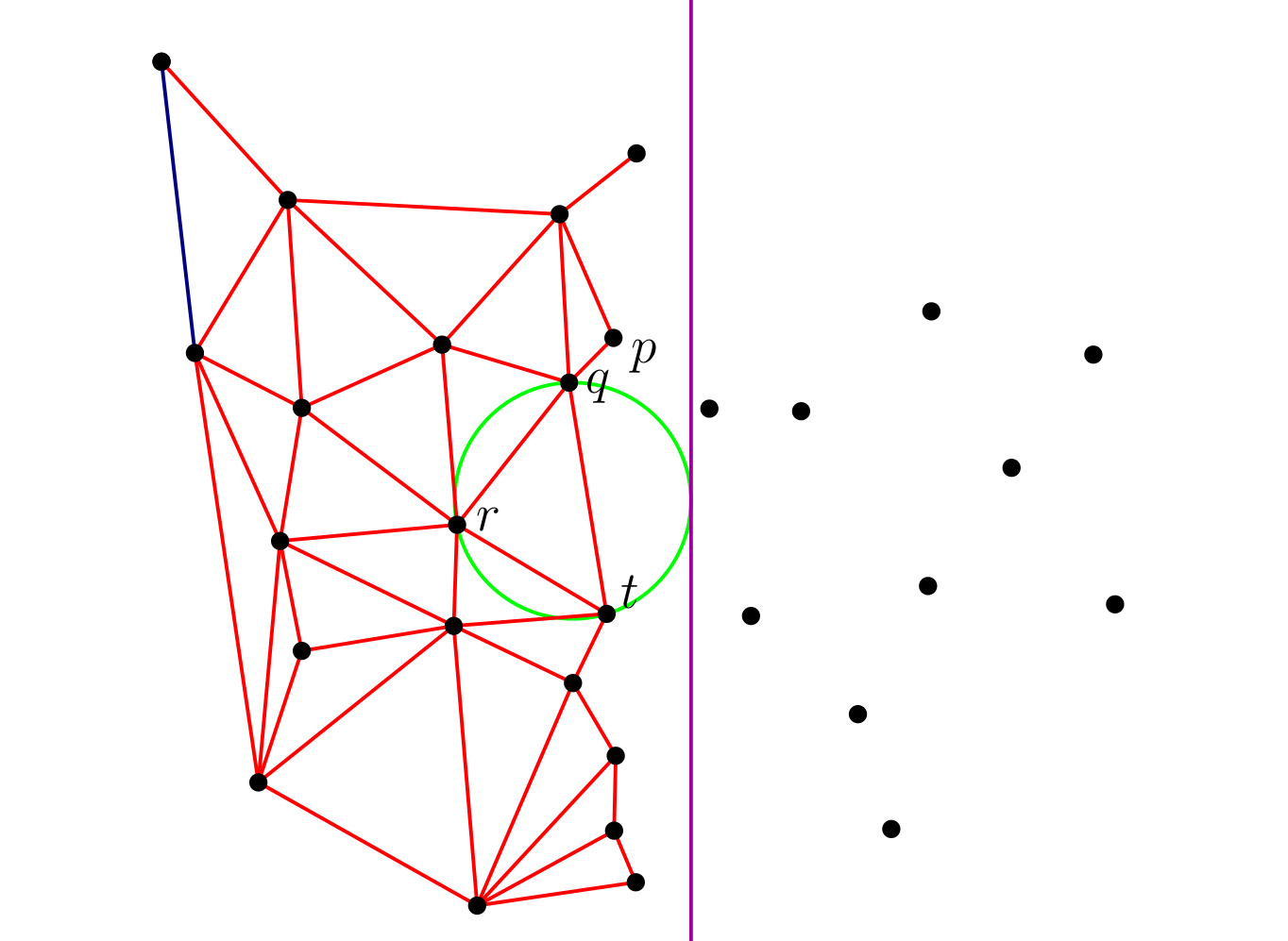
Idea
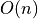
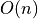

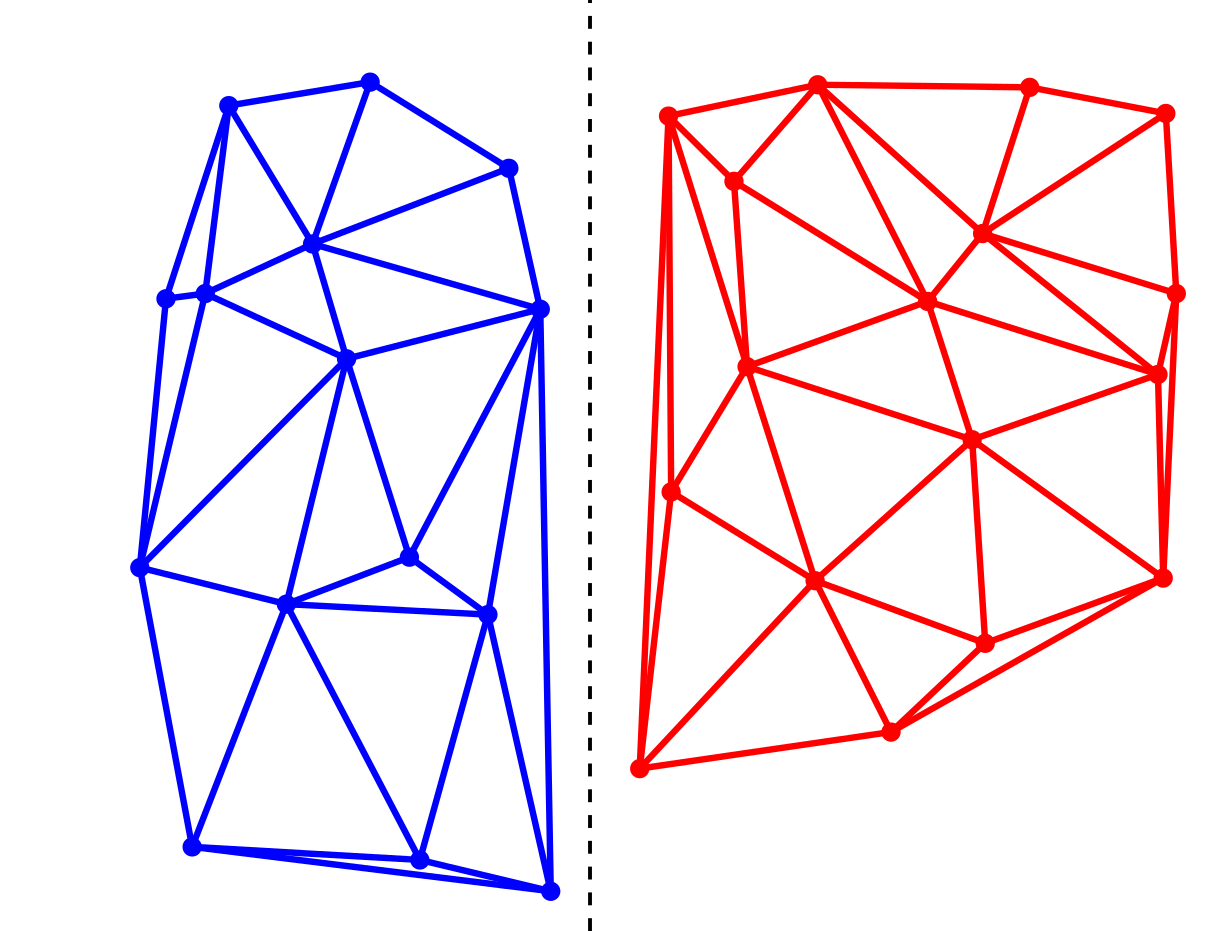
|
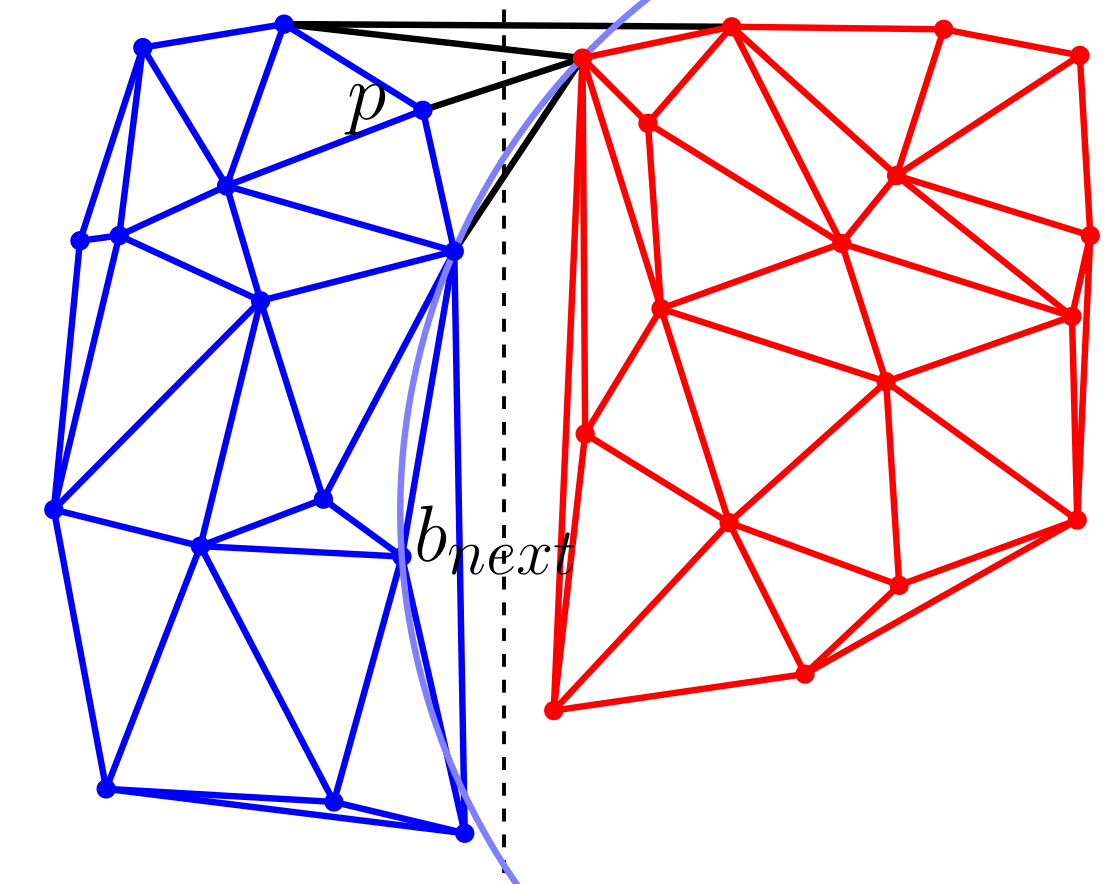
|
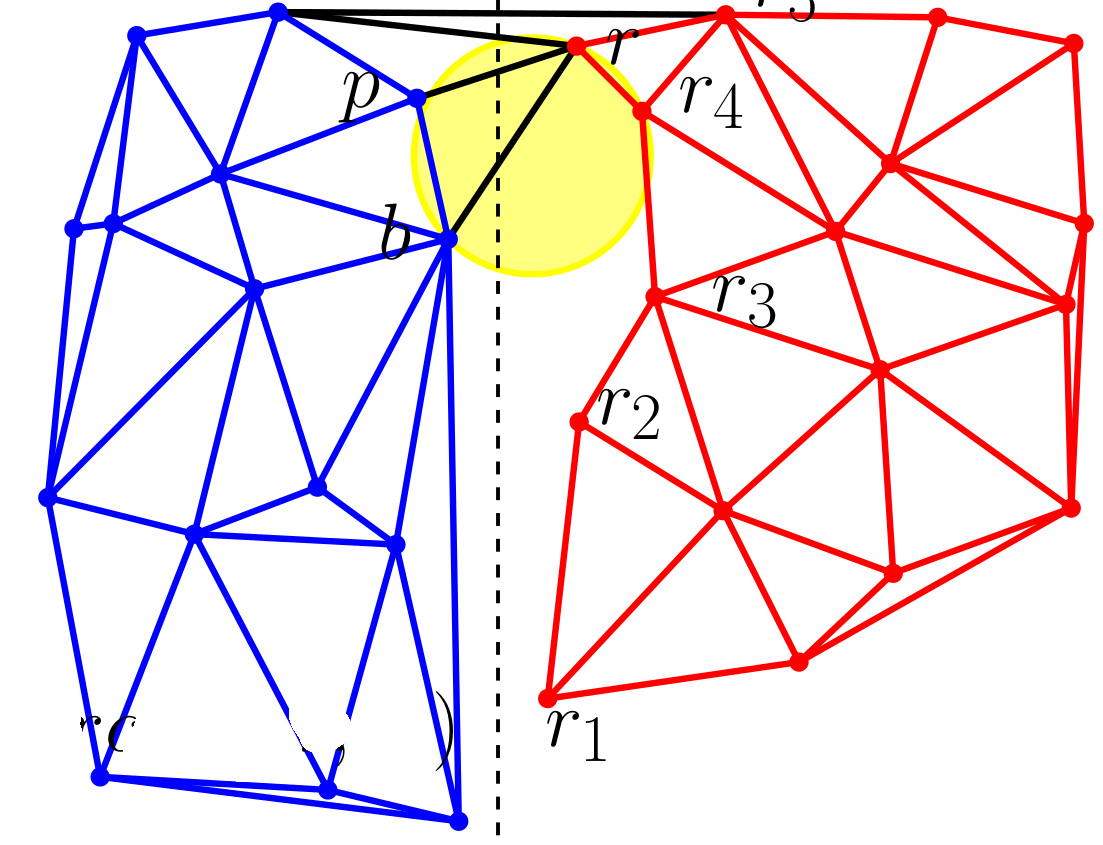
|
|
Idea
Delaunay triangulation has the same structure as the convex hull of projected points to a paraboloid
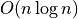 for 3D convex hull
for 3D convex hull 
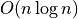 for 2D Delaunay triangulation
for 2D Delaunay triangulation