Computational Geometry: Digital Delaunay Triangulation and Applications§
| author: | David Coeurjolly |
|---|
| author: | David Coeurjolly |
|---|
Input
local consistency of points
![[0,N]^d](_images/math/3950b2b1cd998a687b8fad7f54f86ca1536694f9.png)
specific integer based structures
Let’s start with good news
… and the bad ones
 perturbation can be done
perturbation can be doneQuestions
Can we expect better bounds for Delaunay structure?
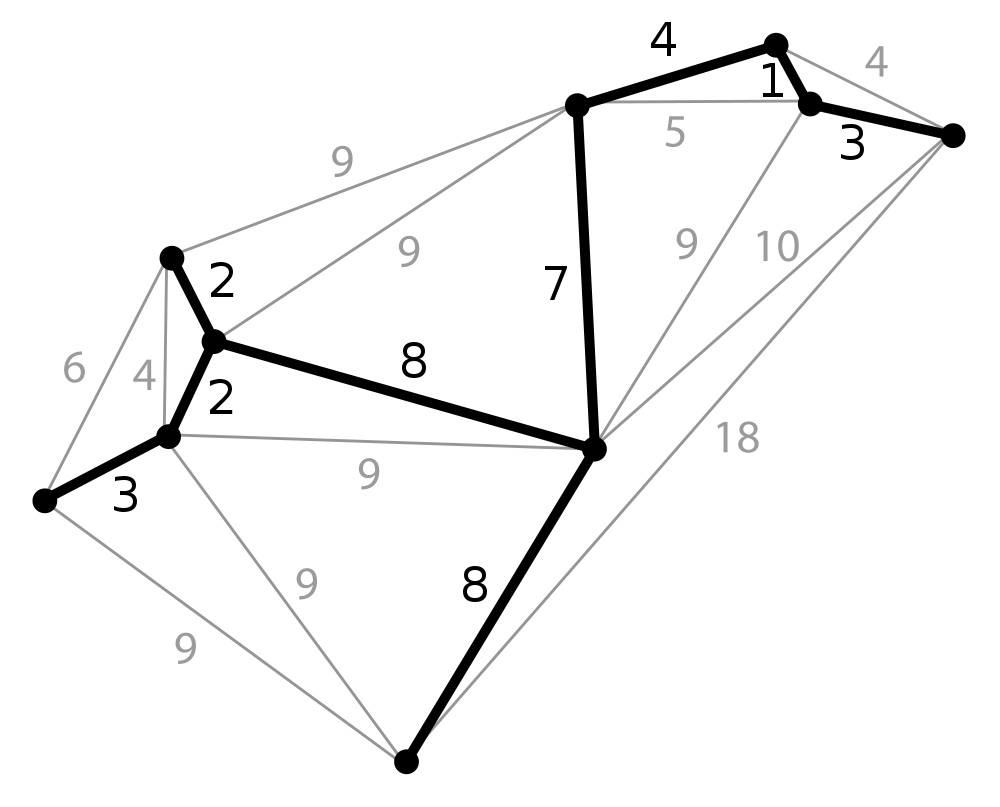
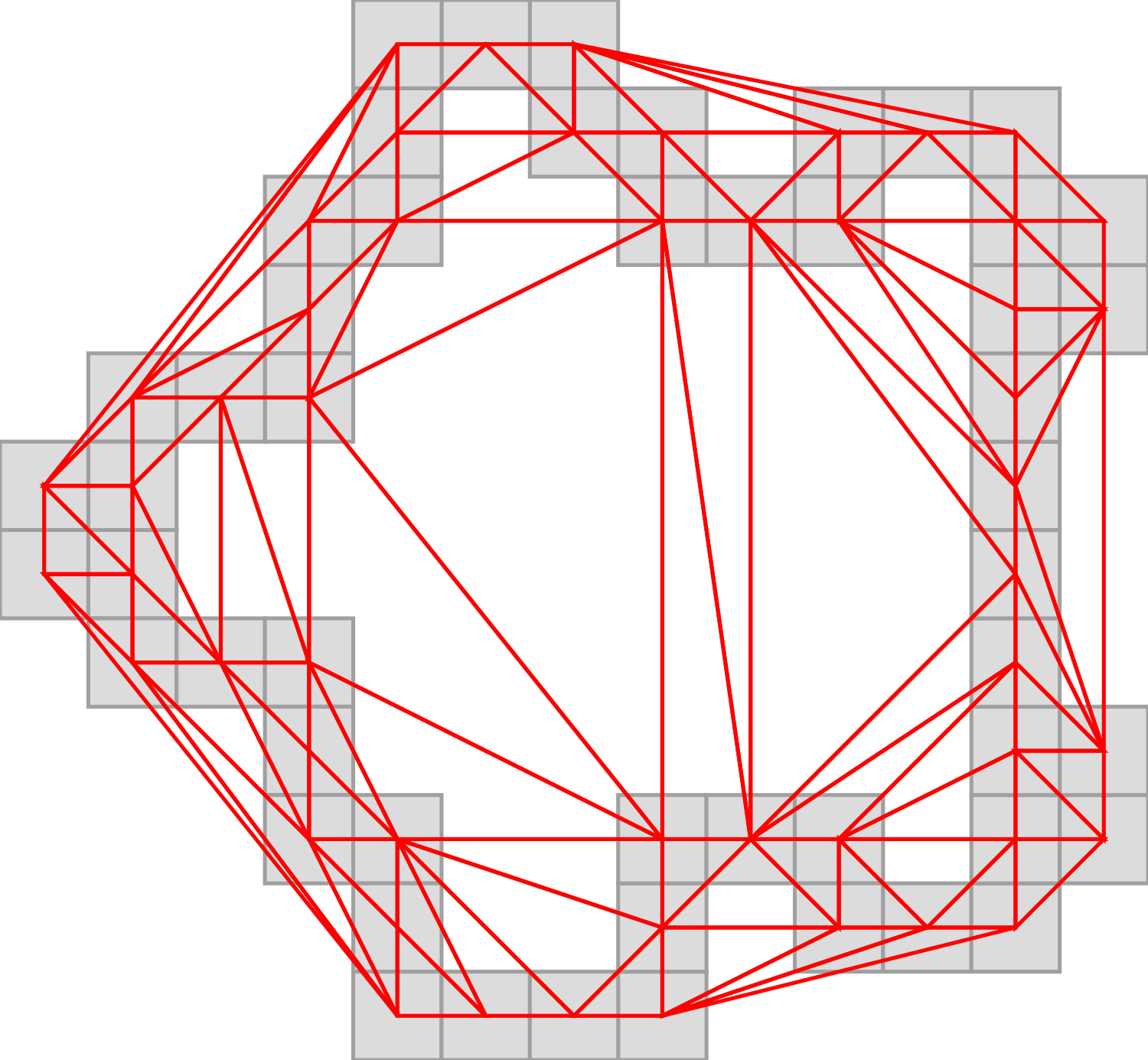
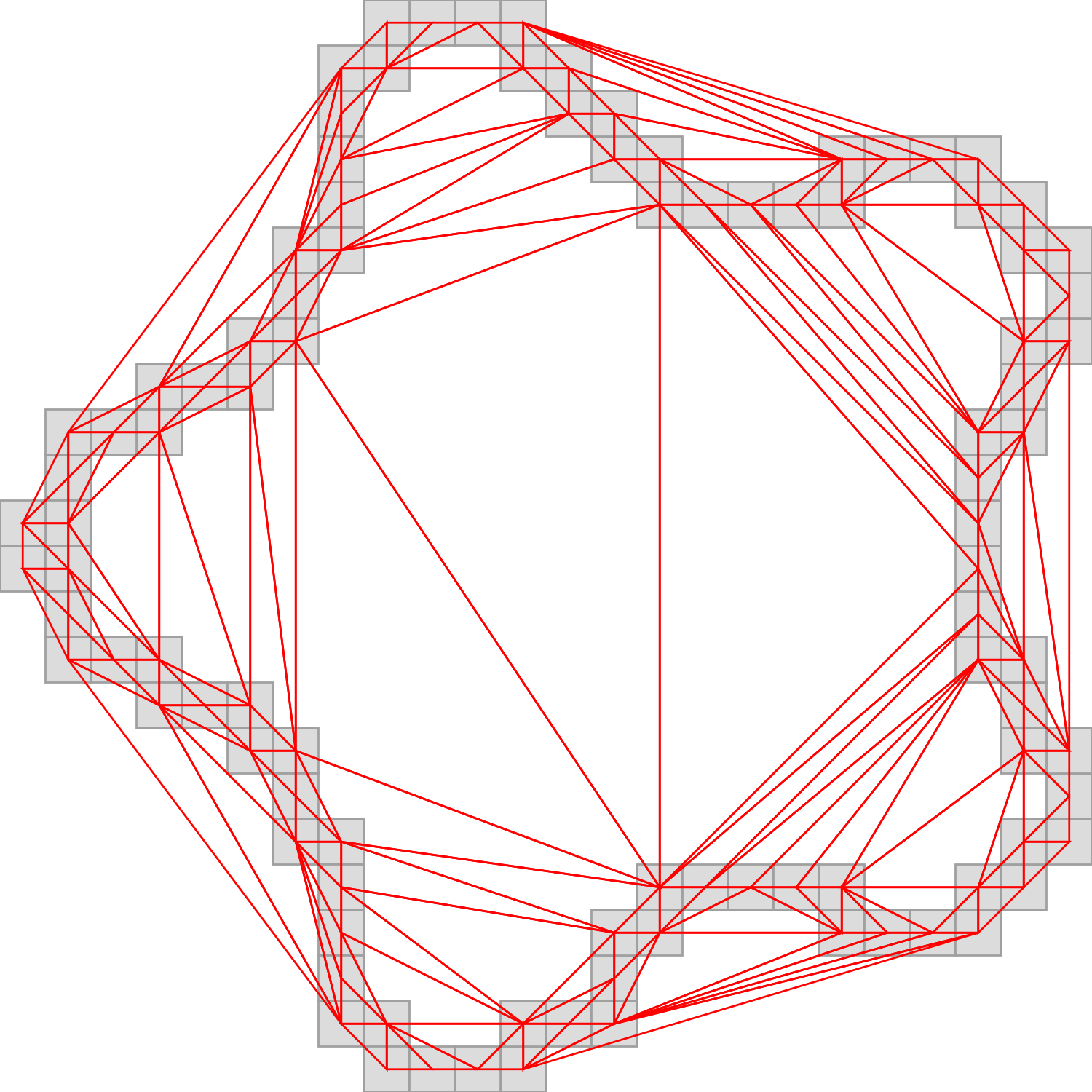
Delaunay triangulation from minimum spanning tree
Thm. [Devillers]
If the Euclidean Minimum Spanning Tree of the input point set,
the whole triangulation can be constructed in expected time 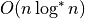
(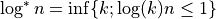 hence for
hence for 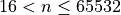 ,
, 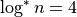 ,
, 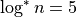 for
for 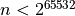 )
)
Why?
Main observation
Thm.
The polyline defined from digital contour points is a Delaunay spanning graph with maximal degree 2
Thm.
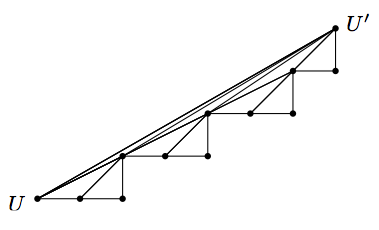
Expected time for Delaunay construction for digital contour is in 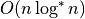
|
|

|
Observation
For digital straight segment patterns, can we recover the Delaunay structure from arthimetic properties?
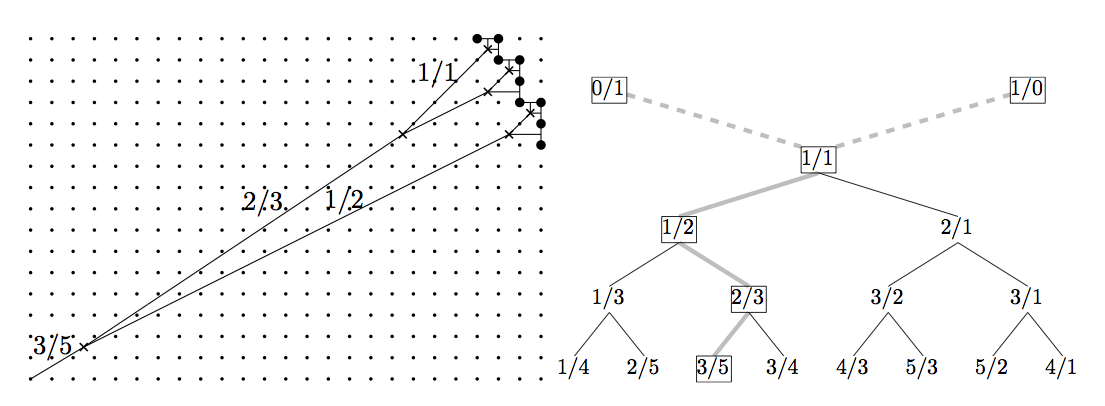
 Yes! [Roussillon, Lachaud]
Yes! [Roussillon, Lachaud]
Setting
 domain
domainMain Result
Thm. [Chan]
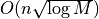 expected randomized time for Delaunay Triangulation construction
expected randomized time for Delaunay Triangulation construction
Key Data Structure: Van Emde Boas Tree
 !!
!!Settings
Set 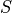 with
with 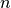 points sampling/approximating a smooth 2-manifold C can I reconstruct a discrete manifold M such that
points sampling/approximating a smooth 2-manifold C can I reconstruct a discrete manifold M such that
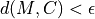 for some metric d (e.g. Haussdorff)
for some metric d (e.g. Haussdorff)Variants
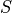 has good sampling properties
has good sampling properties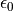 (e.g. at least
(e.g. at least 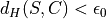 ), then for samplings with
), then for samplings with
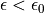 Algorithm A produces a discrete structure
homeomorphic to C
Algorithm A produces a discrete structure
homeomorphic to CSampling Definition
Def.
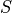 is an
is an  -sampling of
-sampling of 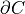 if
if
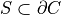 and
and 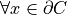 ,
, 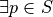 such that
such that 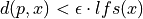 .
.
with lfs(x) being the local feature size at x: 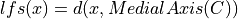
 -samples are on
-samples are on 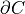
 is be used to control the number of samples and its
distribution.
is be used to control the number of samples and its
distribution.Question what does 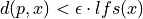 mean?
mean?
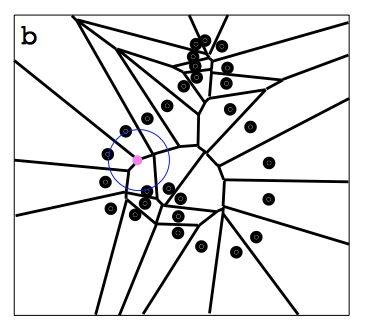
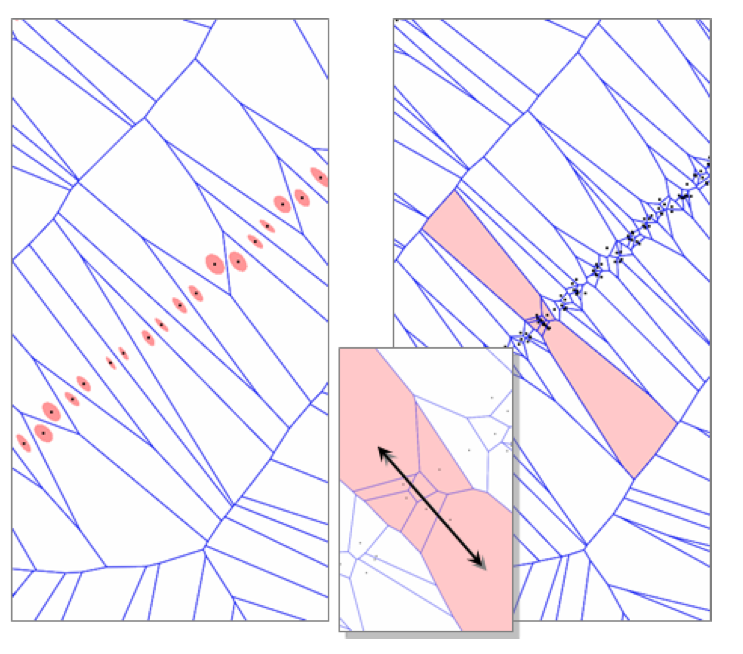
Compute the Voronoi Diagram of  |
|
Compute the Voronoi Diagram of 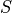 |

|
| Extract the poles and polar balls | 
|
pole of a sample s: pair of power diagram vertices farthest from s on either the inside or outside of the “object”.
Compute the Voronoi Diagram of 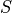 |

|
| Extract the poles and polar balls | 
|
| Compute the Power Diagram of such poles | 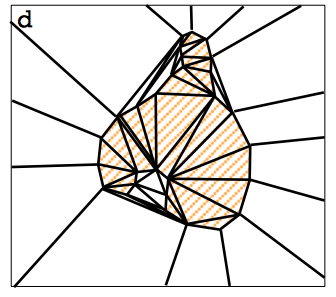
|
Compute the Voronoi Diagram of  |

|
| Extract the poles and construct | 
|
| Compute the Power Diagram of such poles | 
|
| Extract the power crust | 
|
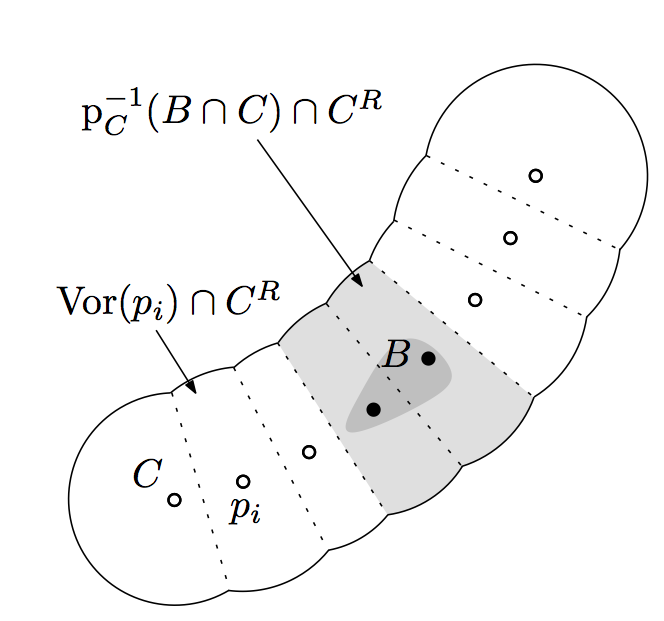
Thm.
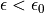
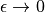
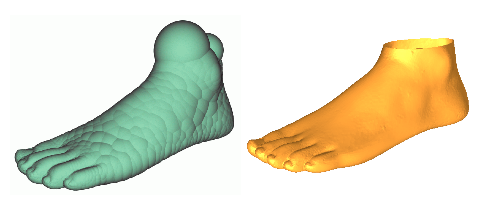
|

|
Side-product of Power Crust
Thm.
Direction 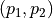 from poles
from poles 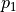 and
and
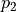 at a sample s is a convergent
(w.r.t.
at a sample s is a convergent
(w.r.t.  ) estimation of the normal
direction at s
) estimation of the normal
direction at s
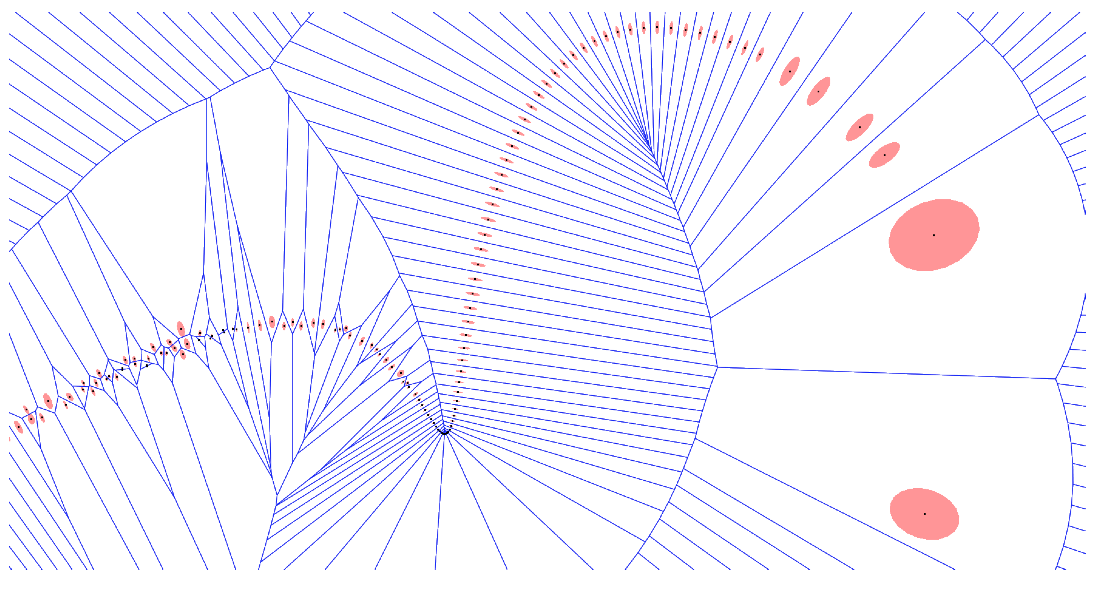
…but very sensitive to noise or sampling conditions
keep in mind that in theorems, 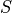 samples C exactly
samples C exactly
Alternative solutions: use Voronoi cell covariance matrix [Alliez]
Idea
Covariance matrix is still a key tool but it is evaluated on r-offest of the input set
Thm.
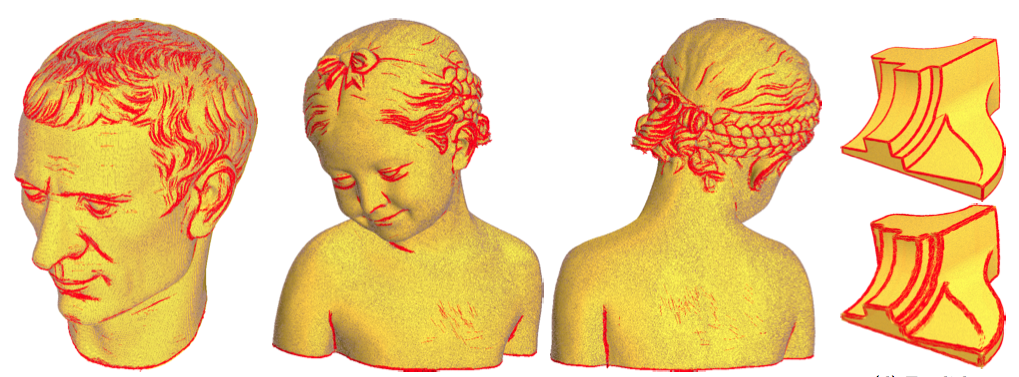
Eigenvalues/Eigenvectors of the covariance matrix at a point are related to principal curvature/principal curvature direction
Convergence results exist with Haussdorff hypothesis on the point set
Robust tool for feature extraction
Idea
Estimate
from
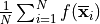 |
|
Many fields
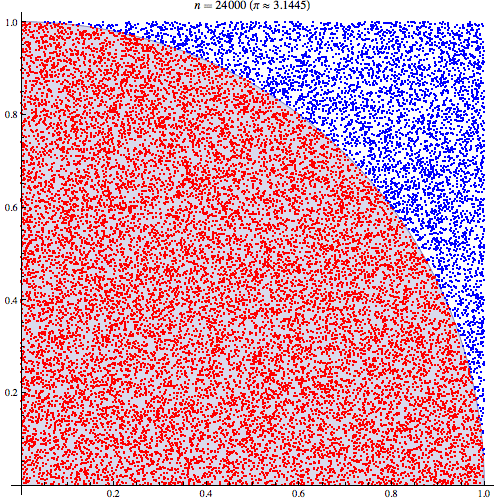
Variance in the Monte-Carlo Integration process (uniform sampling)
Integration error :
Spectral properties
Uniform sampling
Jittered/Stratified sampling

Poisson Disk

Low discrepancy sequences Quasi-Monte-Carlo approaches

Tiled based approaches

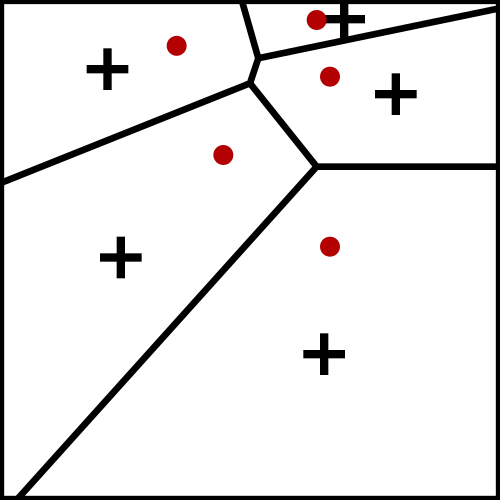
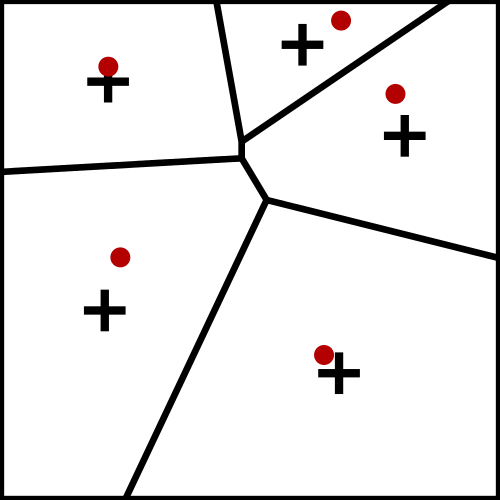
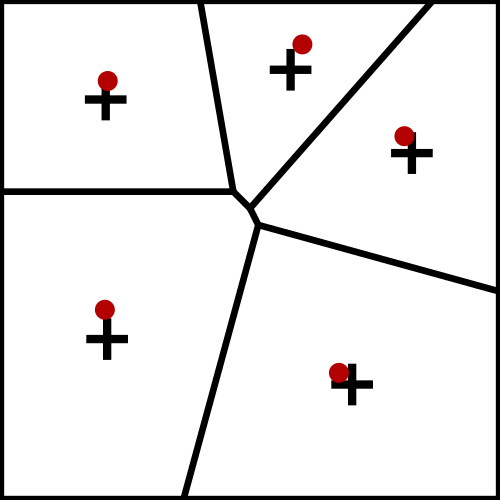
Description Iterative algorithm
Generate N points using uniform sampling
Compute its Voronoi diagram V
while (not(stability))
{
For each cell
Compute its centroid
Move site to the centroid
}
|
|
|
|
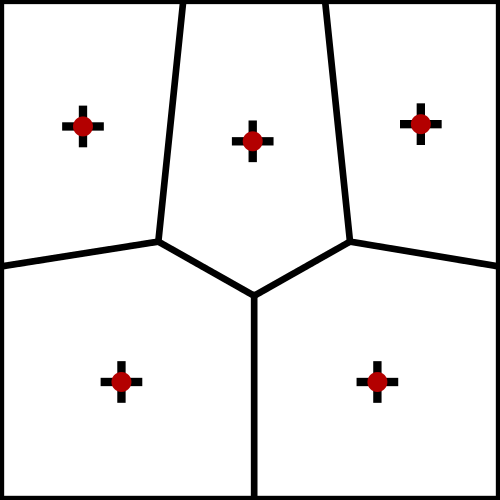
Converges to a stable structure (honeycomb) but if we stop the process, we obtain a reasonable point sampling
[Cohen-Steiner et al]
Equi-distribution of samples  Cells with same capacity
Cells with same capacity
Isotropic influence zone of samples  Energy model on
cell shapes
Energy model on
cell shapes
 iterative process to minimize global energy
iterative process to minimize global energy related to power diagram
related to power diagramDiscrete version


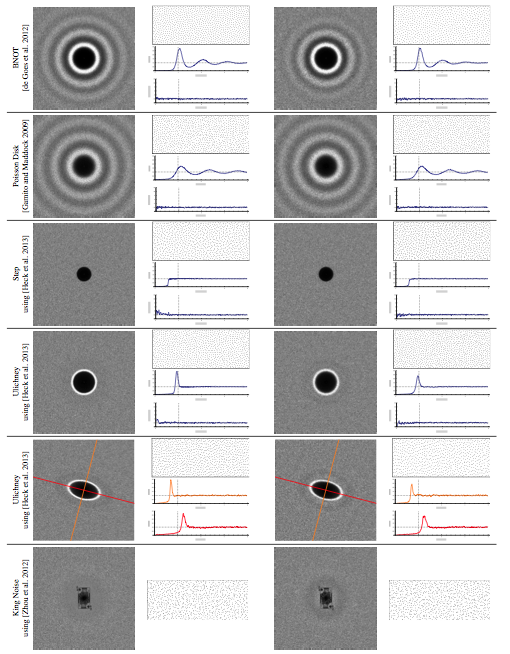
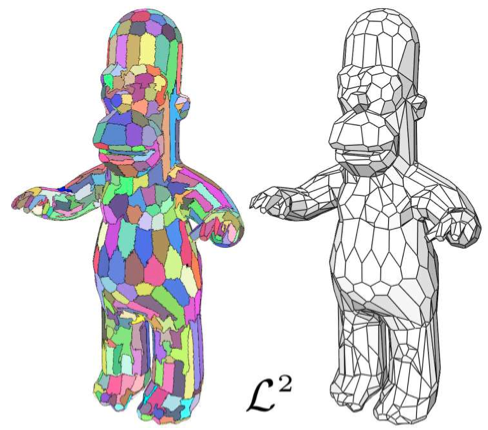
Experimental comparison

|

|