Digital Geometry: Estimators§
| author: | David Coeurjolly |
|---|
| author: | David Coeurjolly |
|---|
Objectives
e.g.
Algorithmic point of view
Multigrid analysis Gauss digitization scheme parametrized by a grid-step
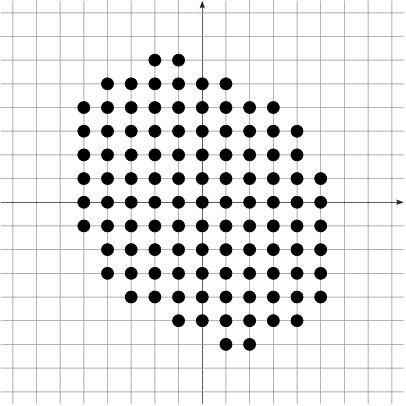
|

|
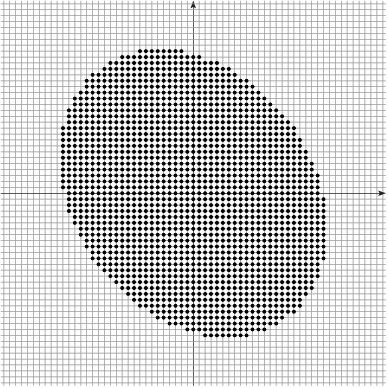
|
Idea
Single scalar quantity attached to a digital object 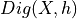
E.g.:
Area in 2D (resp. 3D)
Geometrical moments:
Multigrid convergence definition
Def.
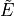 of some geometric quantity
of some geometric quantity 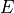 is multigrid convergent for a family of shapes
is multigrid convergent for a family of shapes 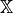 and a digitization process
and a digitization process  iff for all shape
iff for all shape 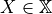 , there exists a grid step
, there exists a grid step 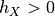 such that the estimate
such that the estimate 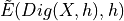 is defined for all
is defined for all 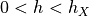 and
and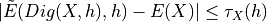
where 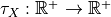 with null limit at
with null limit at  . This function is the speed of convergence of the estimator.
. This function is the speed of convergence of the estimator.
From previous lectures…
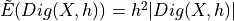 , this estimator converges for convex shapes
, this estimator converges for convex shapes 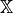 with speed
with speed  [Gauss, Dirichlet]
[Gauss, Dirichlet]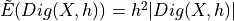 , this estimator converges for
, this estimator converges for  convex shapes
convex shapes 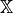 with speed
with speed 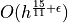 [Huxley]
[Huxley]| Quantity | 1 | 0.1 | 0.01 | 0.001 | … |
|---|---|---|---|---|---|
| h | 1 | 0.1 | 0.01 | 0.001 | … |
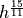 |
1 | 0.04328 | 0.00187 | 0.00008 | … |
Idea
We specify:
A set of elementary displacement or pattern (e.g. 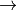 and
and 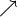 )
)
A weight per displacement vector
Length Estimation sum of weighed occurrences of each pattern
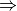 statistical analysis to optimize the weights to minimize errors for random distribution of segments of length
statistical analysis to optimize the weights to minimize errors for random distribution of segments of length 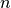
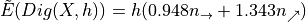
Generalizarion
We decompose the  into pattern of length
into pattern of length 
For each pattern 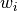 , we consider a weight
, we consider a weight 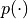
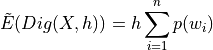
Main Result
Thm.
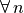 and
and 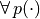 the set of slopes
the set of slopes 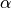 such that the estimator is convergent is countable
such that the estimator is convergent is countable 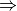 most of the time, the estimator does not converge
most of the time, the estimator does not converge
[Tajine,Daurat]
Solution locally adapt the parameter m ? set m as a function of h ? (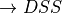 )
)
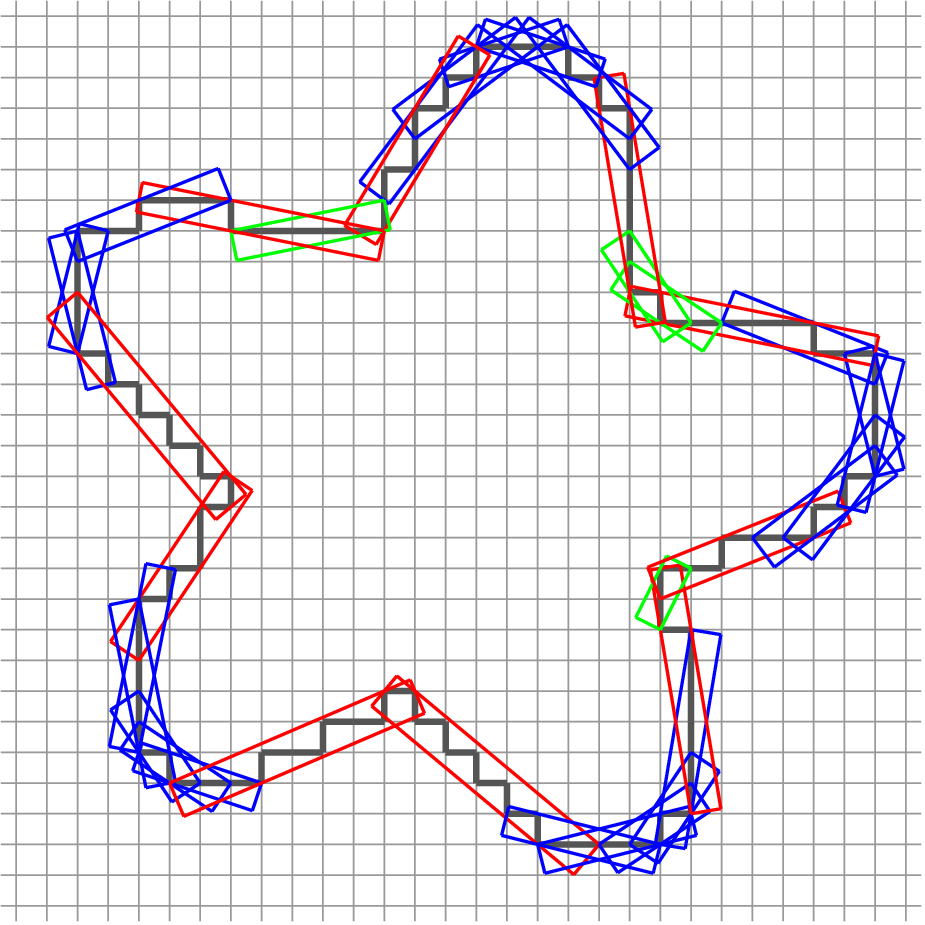
Basic Idea
Compute the decompostion of the contour 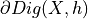 into maximal DSS
into maximal DSS 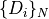 (with thus
(with thus 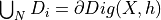 )
)
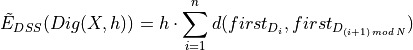
Main result
Thm.
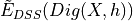 is multigrid convergent for convex shapes with speed
is multigrid convergent for convex shapes with speed 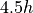
We need
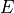 is defined
is defined
|

|
|

|

|

|
|
|
|

|
|
|
Principle
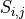 defines a piece of the contour from index
defines a piece of the contour from index 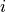 to
to 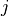
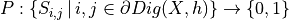 (e.g. being a DSS, a DCA,…)
(e.g. being a DSS, a DCA,…)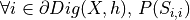
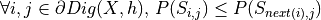
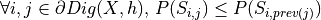
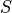 is maximal if
is maximal if 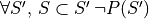
Maximal covering = set of all maximal segment of 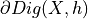
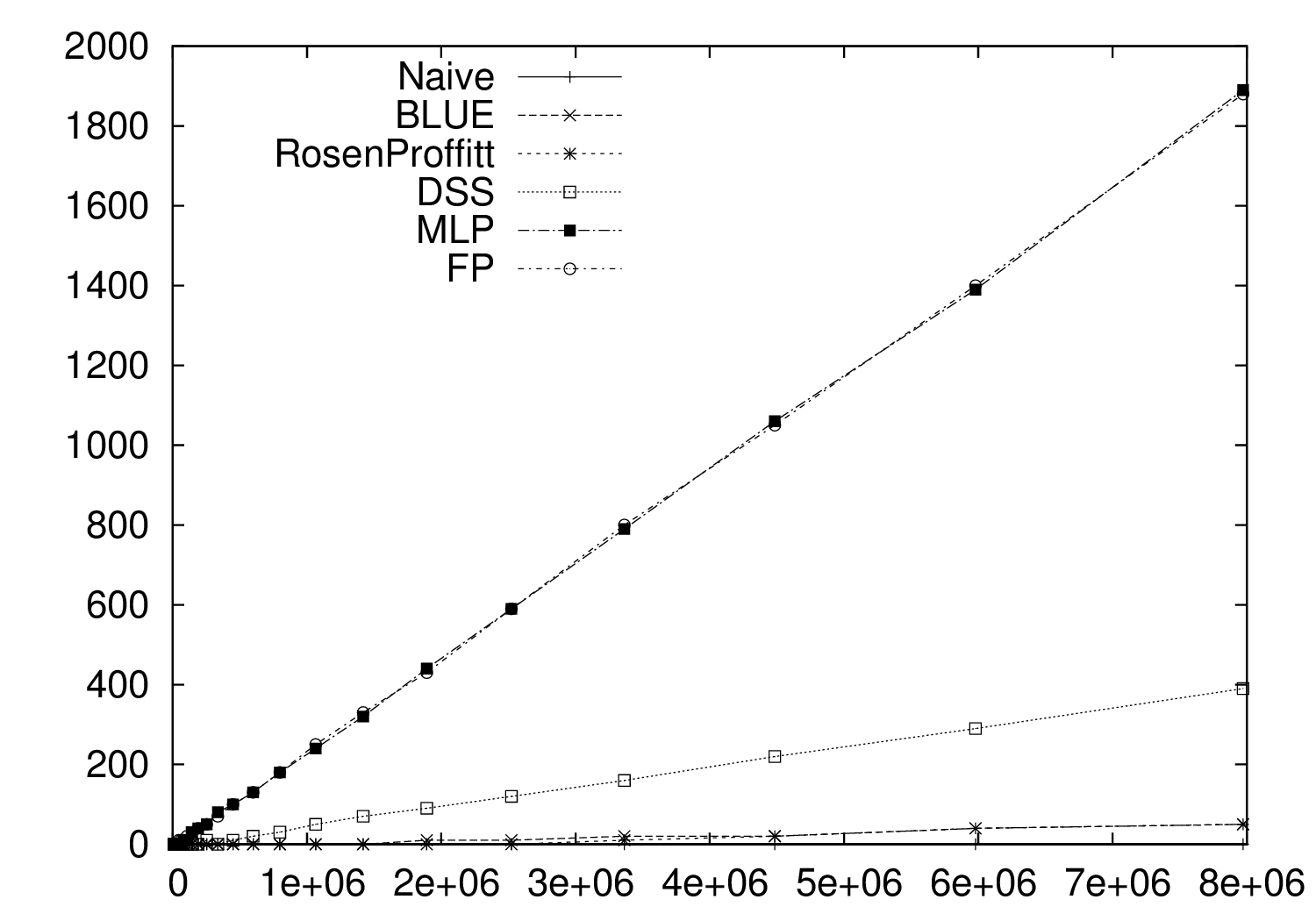
Algorithmic point of view
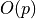 per operations
per operations 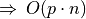
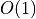
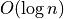

|
|

|

|

|
|
|
|
| X | 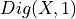 |
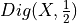 |
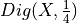 |
Useful to
Idea digital version of
Hence:
Main result: If 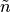 uniformly converges in
uniformly converges in 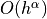 ,
, 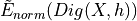 converges in
converges in 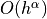
Multigrid convergence for local geometric quantities
Def.
The estimator 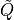 is multigrid-convergent for the family
is multigrid-convergent for the family 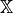 if and only if, for any
if and only if, for any 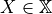 , there exists a grid step
, there exists a grid step 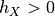 such that the estimate
such that the estimate 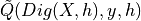 is defined for all
is defined for all 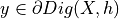 with
with 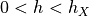 , and for any
, and for any 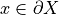 ,
,
with
where 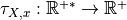 has null limit at 0. This function defines the speed of convergence of
has null limit at 0. This function defines the speed of convergence of 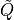 toward
toward 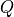 at point x of
at point x of 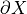 . The convergence is uniform for
. The convergence is uniform for 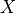 when every
when every 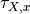 is bounded from above by a function
is bounded from above by a function 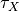 independent of
independent of 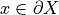 with null limit at 0
with null limit at 0
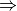 we need a mapping
we need a mapping 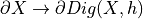
 Uniform convergence is a strong constraint
Uniform convergence is a strong constraint
Generic fitting approach
Fix a neighborhood 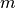 around a point
around a point 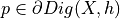
Fit the 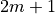 digital points
digital points 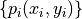 by a function
by a function 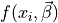 with parameter vector
with parameter vector 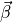
Least-square fitting : Minimize quadratic error:
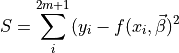
E.g., 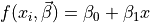 for linear fitting.
for linear fitting.
Example: tangent vector estimator
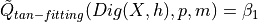 where
where 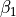 is the result of a least-square linear fitting
is the result of a least-square linear fitting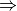 No convergence results for fixed
No convergence results for fixed 
Trivial idea Use a kind of symmetric maximal DSS to estimate the tangent
Algorithmic
More flexible approach Maximal segment from mxaimal covering
If the curve is locally linear, 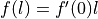 , and
, and
If the curve has curvature greater than 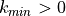 , Taylor decomposition gives us:
, Taylor decomposition gives us:
Convergence Result
Prop.

with 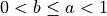
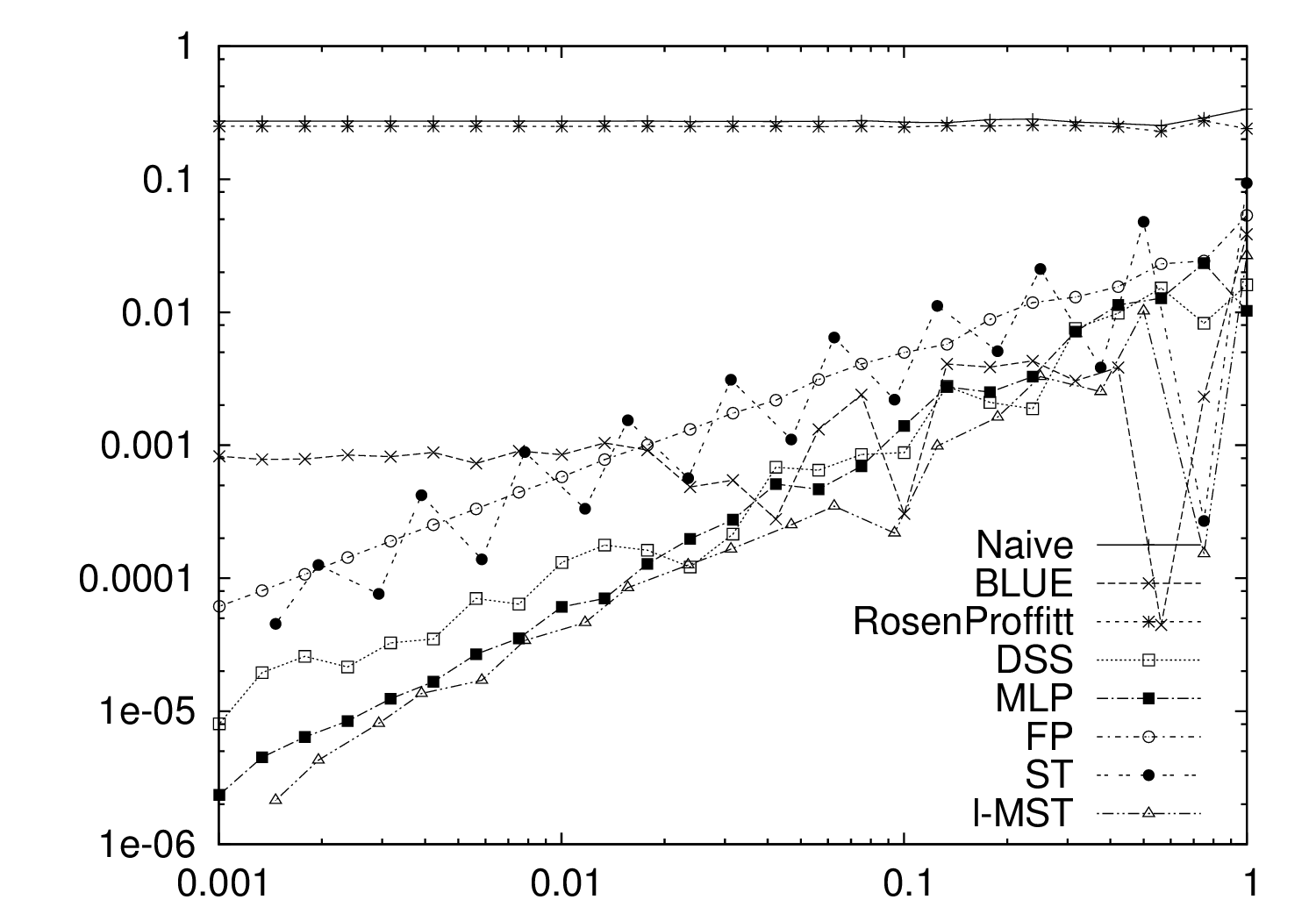
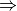 Length of maximal DSS is crucial !
Length of maximal DSS is crucial !
Fitting an order-2 polyonmial
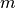 value
valueChord length approach
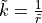 with
with 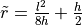
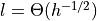 (see below)
(see below)Circumscribing circle from two half-tangent
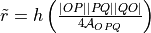
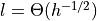 (see below)
(see below)Nice but 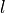 is not in
is not in 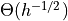
We need to consider the following quantities
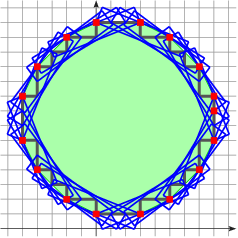
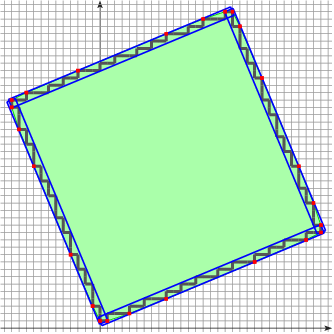
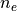 the number of edges of the convex hull of
the number of edges of the convex hull of 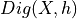
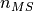 the number of maximal segments in the covering of
the number of maximal segments in the covering of 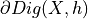
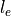 length of convex hull edge
length of convex hull edge  (
(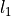 metric for (1)-contours)
metric for (1)-contours)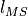 length of a maximal segment (
length of a maximal segment (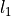 metric for (1)-contours)
metric for (1)-contours)Then, we want to compute:
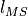
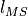
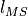 value
valueEverything as functions of h and considering specific shape family 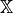
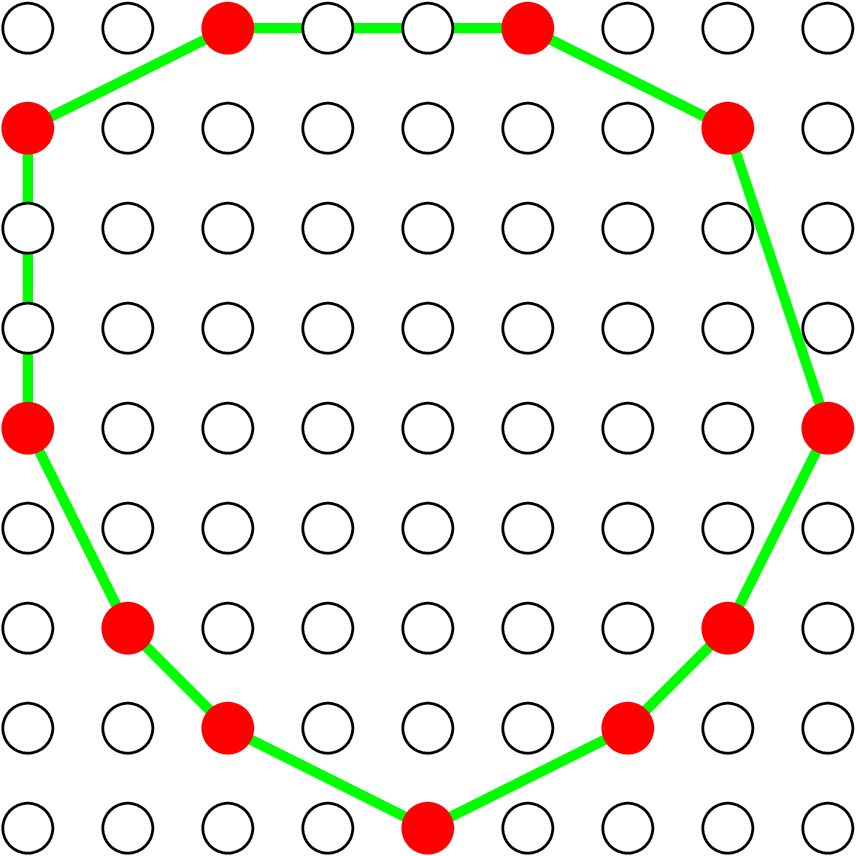
Convex hull of X smallest convex set containing point set X. As consequence of the Def, the convex hull is polygonal convex set with vertices in X
Main result in Lattice polytope in 2D [Barany, Zunic, Balog, Acketa,…]
Thm.
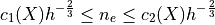
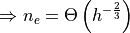
(Similar results in n-D exist)
|

|

|
Main result [Lachaud, de Vieilleville, Feschet]
If 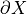 is convex and
is convex and 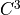
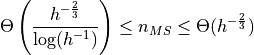
|
|
 |
 |
(Length = 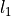 distance for (1)-contours)
distance for (1)-contours)
Results on the sum of lengths
From [Lachaud, de Vieilleville, Feschet]
Hence
If 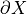 is convex and
is convex and 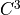
| Quantity | Smallest MS length | Average MS length | Largest MS length |
|---|---|---|---|
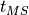 |
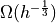 |
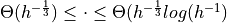 |
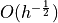 |
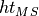 |
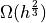 |
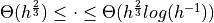 |
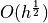 |
(Hints for 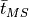 , the lower bound = lower bound on
, the lower bound = lower bound on 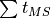 / upper bound
/ upper bound 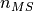 , results for smallest/largest MS require couple of more steps)
, results for smallest/largest MS require couple of more steps)
 Any slope of MS containing P provides multigrid convergent estimation of tangent at P
Any slope of MS containing P provides multigrid convergent estimation of tangent at P
Tangent Estimation in 2D
Curvature Estmiation in 2D
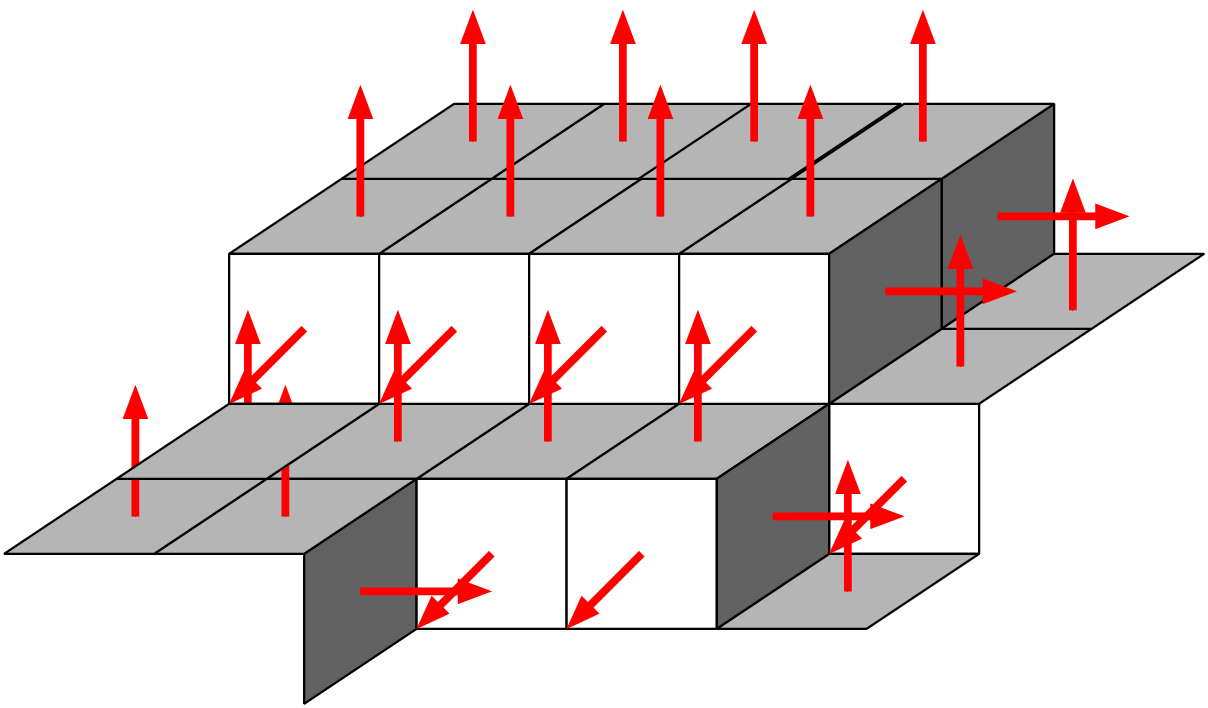
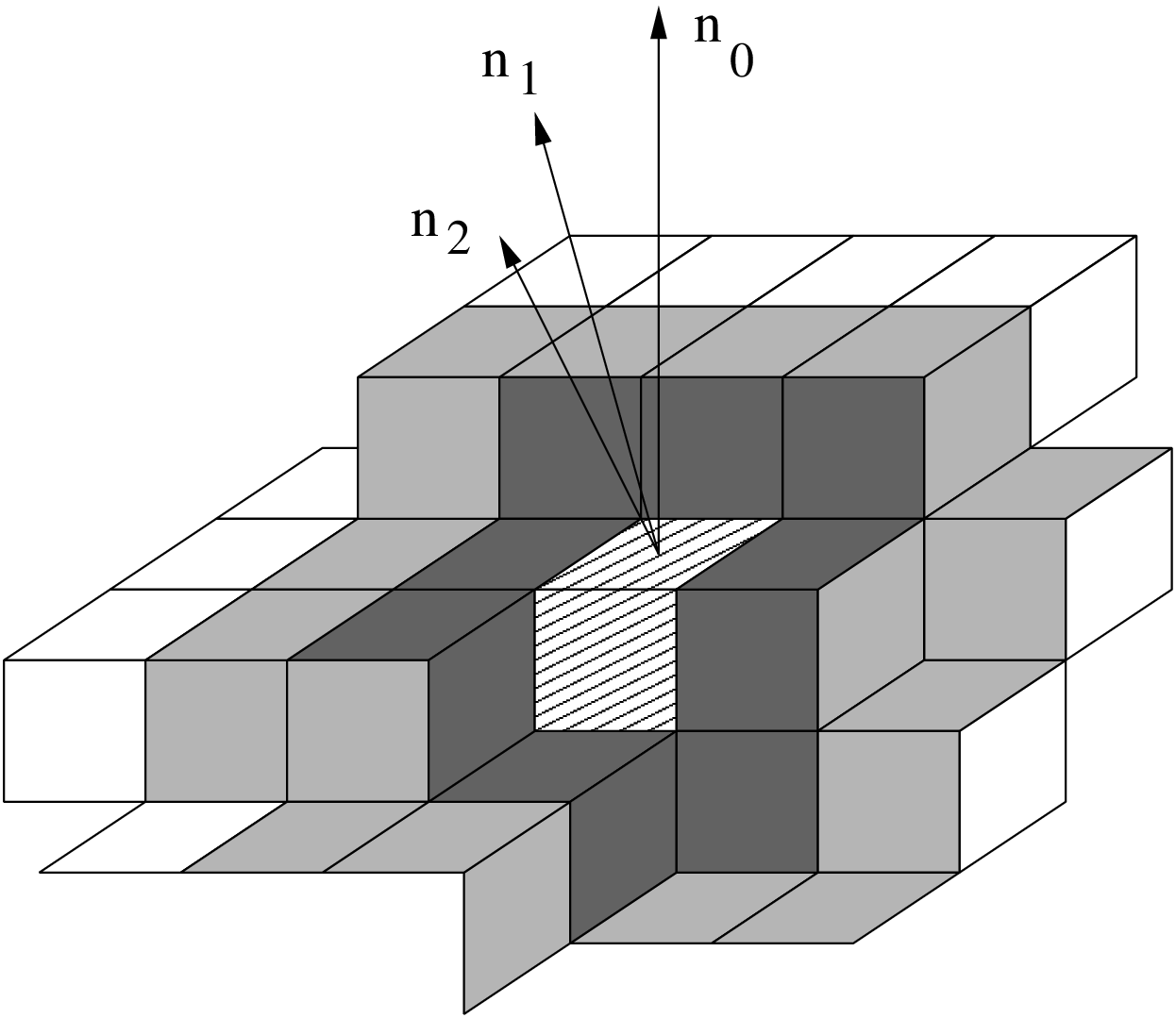
Slice based approaches
 normal vectors
normal vectors
|
|
Convolution based approaches
Convolution of elementary normal vectors in a given neighborhood
|
|

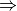 still have to fix a neighborhood parameter
still have to fix a neighborhood parameter
Digital Plane Recognition approaches
… but …
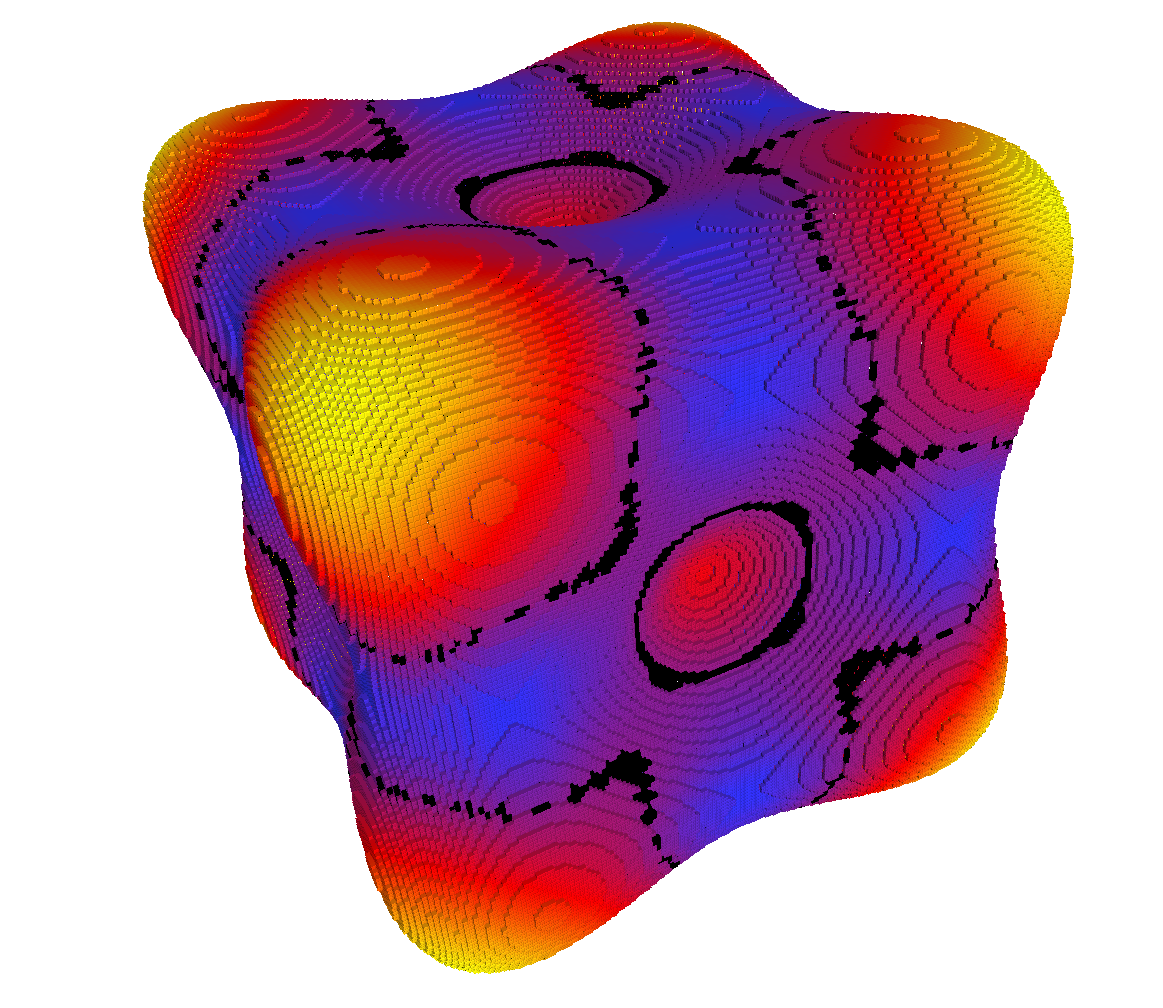
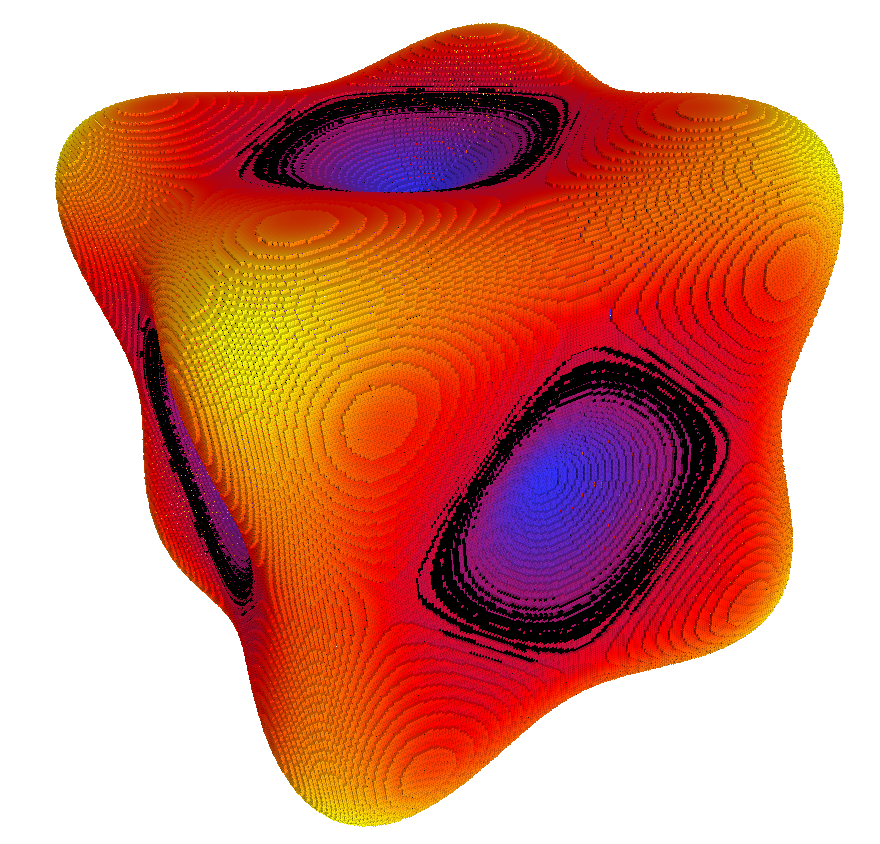
Mean and Gaussian curvature
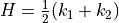
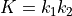
Fitting an implicit polynomial surface is still doable but we need information on the neighborhood
Integral Invariant approach neighborhood in 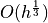 seems to be required
seems to be required
Idea compute area of the intersection between a ball 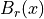 and
and 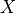 at
at 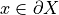
Then, from Taylor expansion and for 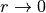
Hence,
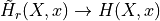 by definition when
by definition when 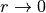
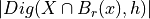
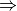 first error term induced by [Gauss,Huxley] (O(h))
first error term induced by [Gauss,Huxley] (O(h))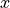 and
and 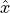 (back-projection used here)
(back-projection used here)Main Result
Thm.
For a family of shape with onvex 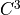 -boundary and bounded curvature,
-boundary and bounded curvature, 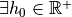 , for any
, for any 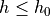 , setting
, setting 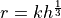 , we have
, we have
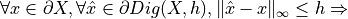
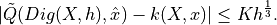
(similar bound in 3D)
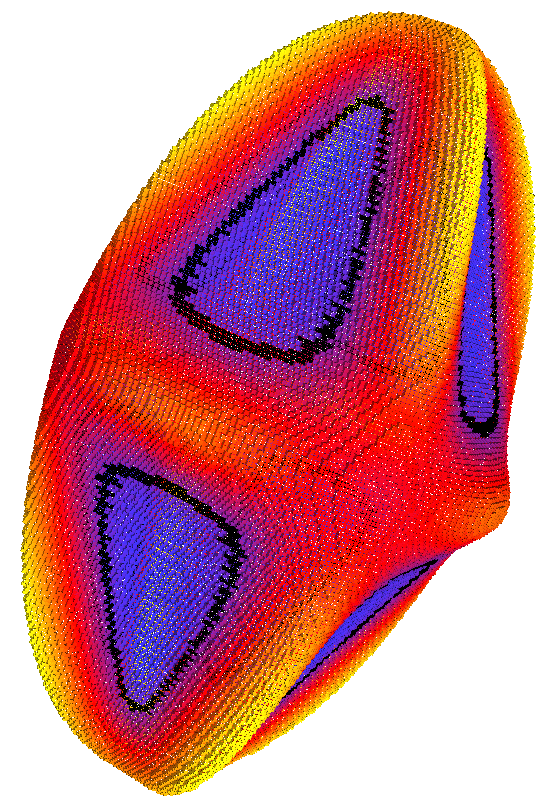
Idea
Instead of computing the volume of 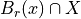 , we compute its covariance matrix
, we compute its covariance matrix
Eigenvalues of 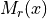 are such that:
are such that:
Result
Similar convergence results exist with speed 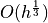
Experimental analysis confirms the 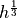 neighborhood size
neighborhood size
|
|
|

|

|

|
First, let’s have a look to the theorem statement
Thm.
For a family of shape with convex 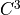 -boundary and bounded
curvature,
-boundary and bounded
curvature, 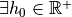 , for any
, for any 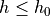 , setting
, setting 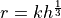 , we have
…………
, we have
…………
To have the convergence, we need the radius to be in
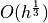
We know that
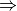 Let’s use (square of) average MS length to define r
Let’s use (square of) average MS length to define r
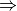 Parameter-free convergence in
Parameter-free convergence in
 !
!
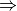 Automatic selection of the scale parameter
Automatic selection of the scale parameter

|

|

|
|

|

|
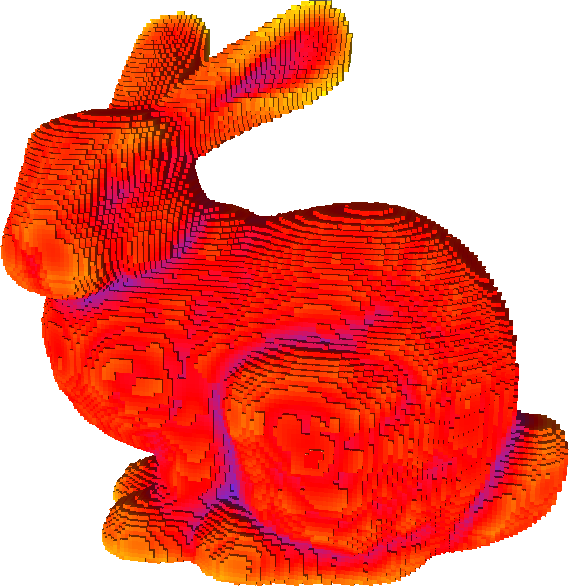
Idea Use scale-space behavior of II estimators to classify surfels into flat,smooth,edge regions

|

|

|

|
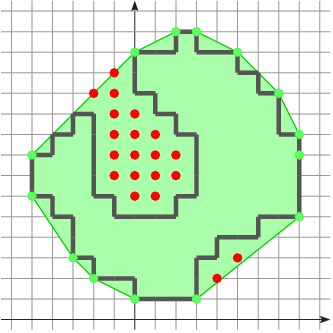
Simple definition
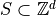 is digitally convex iff there exists
convex shape
is digitally convex iff there exists
convex shape 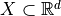 such that
such that 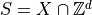

|
|
Let  be a (1)-curve
be a (1)-curve
Properties on convex hull
 is a period of some DSS
is a period of some DSS is a leaning point for some period of some DSS
is a leaning point for some period of some DSSMain result [Debled-Rennesson, Doerksen-Reiter]
Thm.
S is digitally convex 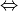 slopes of maximal segment in the covering are monotonic
slopes of maximal segment in the covering are monotonic
|
|