Digital Geometry: Contour Analysis§
| author: | David Coeurjolly |
|---|
| author: | David Coeurjolly |
|---|
Objectives
Idea
Starting point + differential code according to adjacency displacement and an orientation
Reversible and unique encoding
Code driven geometrical transformations
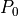
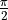
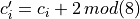 (for (0)-adjacency)
(for (0)-adjacency)Basic length estimator
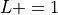 for even codes
for even codes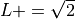 for odd codes
for odd codesGiven a (1)-adjacency, let 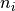 be the number of ith-code
be the number of ith-code
(but may be self-intersecting)
Representation as a word on an alphabet
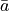 …
…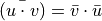
A Polyomino  tiles the plane if and only if its contours has the following structure (up to cyclic rotations)
tiles the plane if and only if its contours has the following structure (up to cyclic rotations) 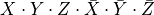 [Beauquier-Nivat]
[Beauquier-Nivat]
Given a digitization model:
Def.
A digital straight line (resp. segment) is the result of a digitization and an Euclidean line (resp. segment)
Digital Segment tracing by Bresenham’s algorithm
GIQ based definition: For each abscissa we consider the closest grid point
Incremental construction
Properties
Segment between 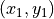 and
and 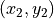 in
in  with slope in [0,1]
with slope in [0,1]
Naive approach
y = y_s
for(i = x_1; i <= x_2; ++i)
display(i,y);
y_real = (y_2-y_1)/(x_2-x_1) * (i+1) + y_1;
dy = y_real - y;
if ( dy > 0.5)
y++;
e = x_2 - x_1
dx = 2*e
dy = 2*(y_2 - y_1)
while (x_1 < x_2)
display(x_1,y_1);
x_1 ++;
e -= dy;
if (e <= 0)
y_1 ++;
e += dx:
Rationale
 inside the loop, 4 integer based operations and one comparison, no possible round-off errors
inside the loop, 4 integer based operations and one comparison, no possible round-off errorsLet us consider GIQ digitization scheme (similar to Bresenham’s) and a straight line 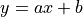 with
with 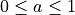 . Let
. Let  be the digitization of the straight line and C its Freeman code
be the digitization of the straight line and C its Freeman code
Thm
<demo>
Periodic structure 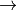 canonical pattern
canonical pattern
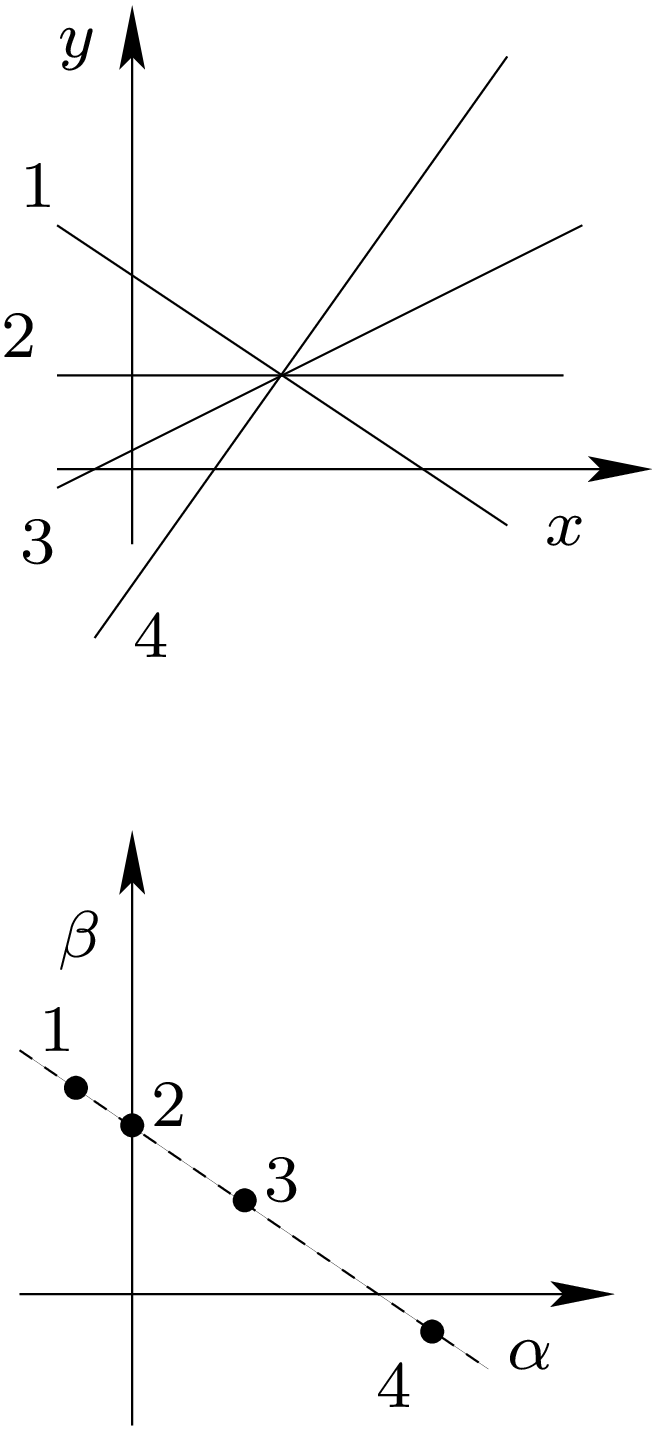
Any two points define a unique straight line

|

|
Two non-parallel straight lines intersects at a single point
|
Single point |

|
Empty set |
|
Non-connected set |
|
Connected set |
 we need to redefine parallelism, intersections, …
we need to redefine parallelism, intersections, …
Switching to another digitization scheme, we may avoid some situations.
E.g. with analytical models, empty set case will never occur
Chordal Property [Rosenfeld]
Evenness Property [Veelaer]
Definition
Def.
Diophantine equation = Equation with integer parameters and solutions in 
Example
(with 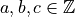 )
)
What is the general form of solutions of such linear diophantine equation ?
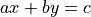 , and let
, and let 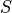 denote the solutions
denote the solutions
Existence
Homogeneous case
General case
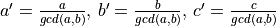
Since 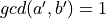 ,
, 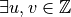 such that
such that 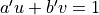 [Bezout]
[Bezout]
Your turn: 12x+15y=51
Idea Design a analytical definition instead of combinatorial ones
Def.
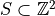 is a analytical DSS with parameters
is a analytical DSS with parameters 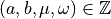 with
with 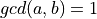 , if for all
, if for all 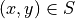 , we have
, we have
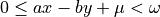
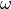 acts as a thickness (arithmetical thickness, >1)
acts as a thickness (arithmetical thickness, >1)
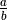 is the DSS slope
is the DSS slope
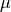 is the arithmetical intercept
is the arithmetical intercept
S is the union of solutions of 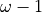 diophantine equations:
diophantine equations:
Thm.
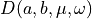
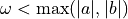 , D is not a (k)-path
, D is not a (k)-path , D is a (0)-arc
, D is a (0)-arc , D is a (1)-arc
, D is a (1)-arc , D is (*)-connected
, D is (*)-connected , D is thick
, D is thick
|
|
|
|
|
| D(3,7,0,5) | D(3,7,0,7) | D(3,7,0,8) | D(3,7,0,10) | D(3,7,0,16) |
Given an Euclidean straight line 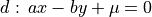 with
with 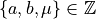 Without loss of generality, we suppose
Without loss of generality, we suppose 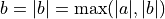
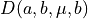 corresponds to a kind of OBQ of d
corresponds to a kind of OBQ of d
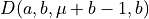 corresponds to a kind of BBQ of d
corresponds to a kind of BBQ of d
![D(a,b,\mu+[\frac{b}{2}],b)](_images/math/61290f76c2bcaf351af5bf128a07c49636d64f25.png) corresponds to the GIQ quantization of d
corresponds to the GIQ quantization of d
![D(a,b,\mu+[\frac{a+b}{2}],a+b+1)](_images/math/8b747b019e0e32965b60d4677f263ddc9846605c.png) corresponds to the supercover digitization of d (analytical digitization with squares)
corresponds to the supercover digitization of d (analytical digitization with squares)
Thm.
Given 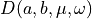 , D is invariant by translation with vector
, D is invariant by translation with vector 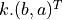 (
(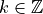 )
)
<proof>
Corollary
Coro.
Any sequence of 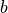 pixels defines a DSS pattern, the pattern is minimal iff
pixels defines a DSS pattern, the pattern is minimal iff 
Similar results than the one obtained by straight segment digitization but more generic
Def.
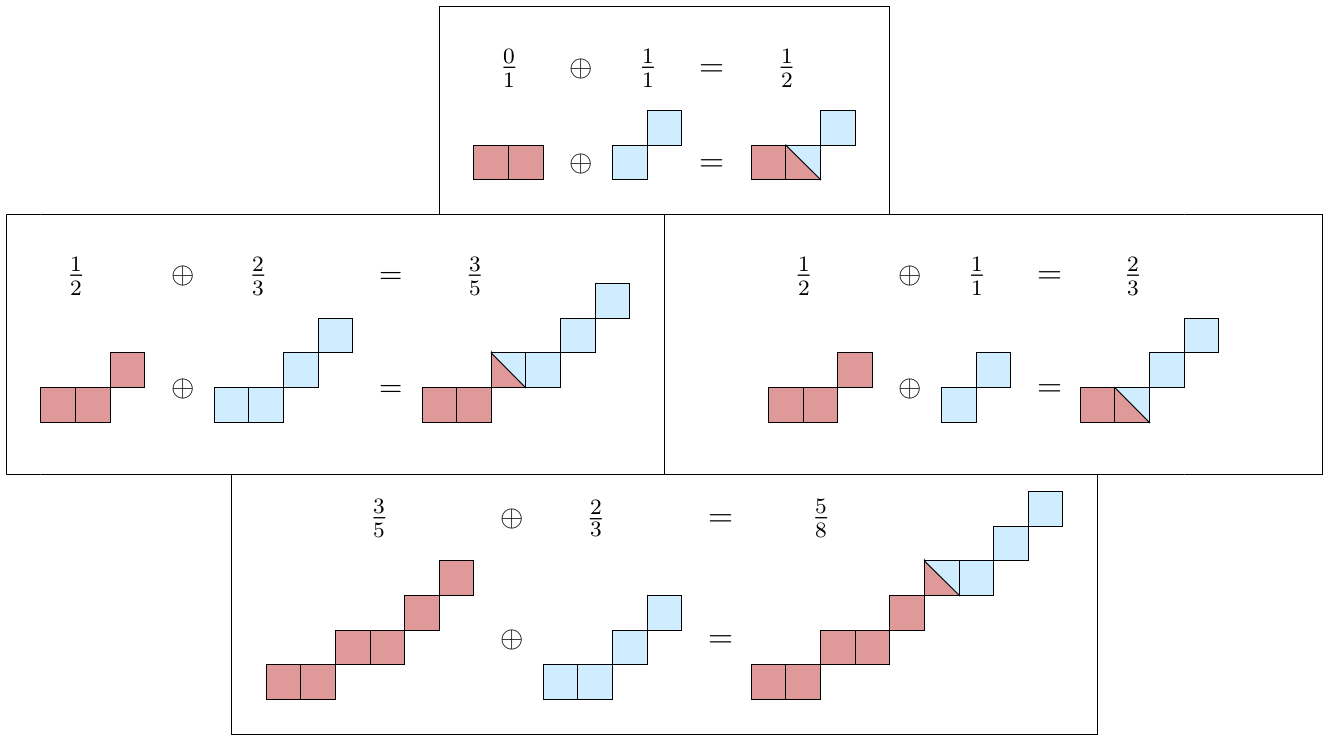
The Farey Series 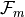 of order m is the ordered sequence of irreducible fractions with denominator less or equal to m
of order m is the ordered sequence of irreducible fractions with denominator less or equal to m
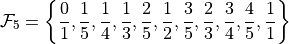
Properties
 et
et 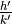 are two successive fractions in
are two successive fractions in 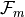 (with
(with 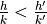 ), then
), then 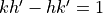
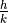 ,
, 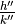 and
and 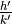 are three successive fractions in
are three successive fractions in 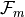 (with
(with 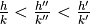 ), then
), then 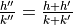 (median fraction)
(median fraction)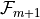 is given from
is given from  inserting median of successive fractions with denominator
inserting median of successive fractions with denominator 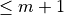
Binary search tree on  fractions
fractions
Given
 with slope
with slope 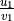 and Freeman code of one of its pattern
and Freeman code of one of its pattern 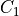
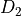 with slope
with slope 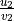 and Freeman code of
one of its pattern
and Freeman code of
one of its pattern 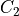
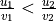
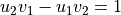 (unimodularity)
(unimodularity)Then
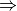
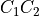 is the Freeman code of one period of the DSS with slope
is the Freeman code of one period of the DSS with slope 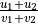
Idea
Given a digital set 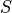 , and a geometrical primitive (DSS,
Digital circle, digital plane, …), decide if
, and a geometrical primitive (DSS,
Digital circle, digital plane, …), decide if 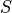 is a subset
of such primitive
is a subset
of such primitive
Detection Yes/No answer
Recognition a valid parametrization of the primitive, the complete set of primitives containing 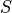 -> preimage
-> preimage
Useful to
Idea
Revert the digitization process and solve a dual problem
DSS: Linear dual space
|
|
|
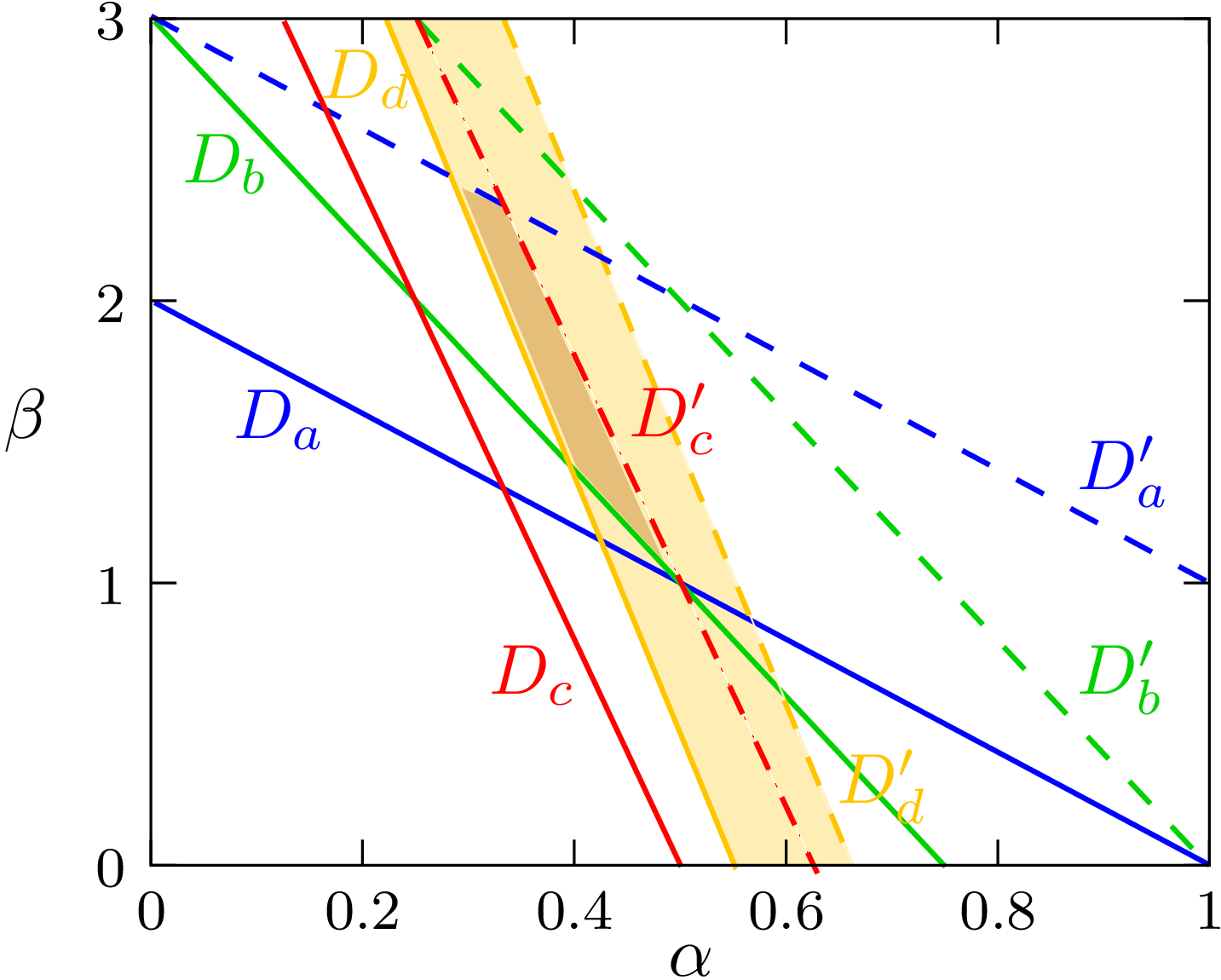
Let us consider the following OBQ digitization scheme of 
Each pixel  contributes to two linear constraints:
contributes to two linear constraints:
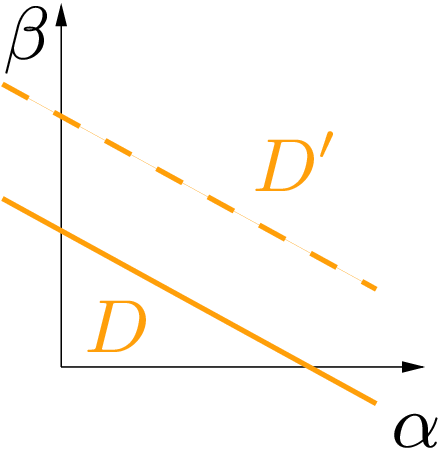
|
Algorithm principle
Given a set S of pixels
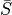 (i.e. we consider DSS in the first octant)
(i.e. we consider DSS in the first octant)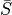 and the two associated constraints
and the two associated constraints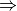 if
if 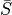 is empty, S is not a DSS (for OBQ scheme)
is empty, S is not a DSS (for OBQ scheme)
 is called the preimage of S
is called the preimage of S
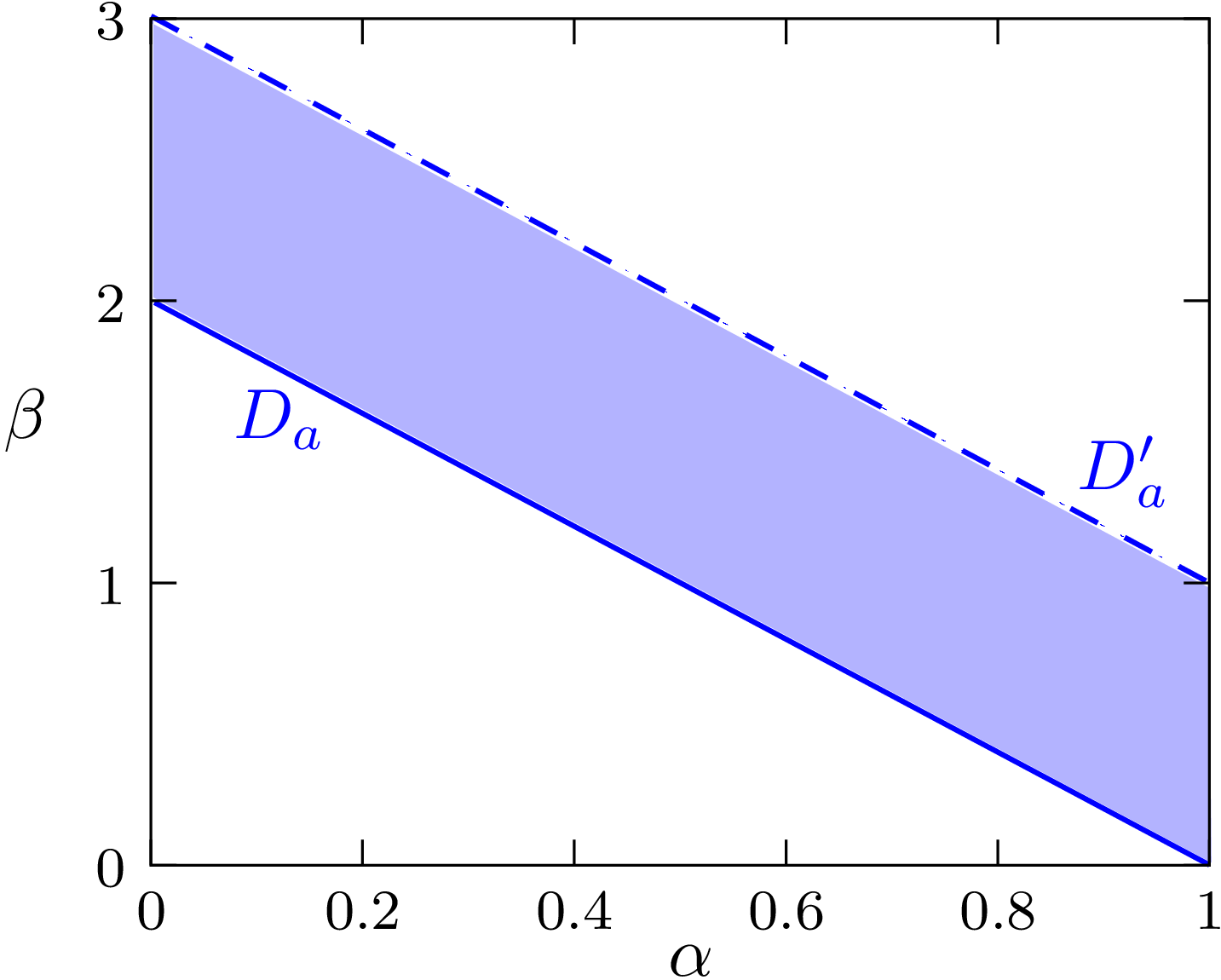
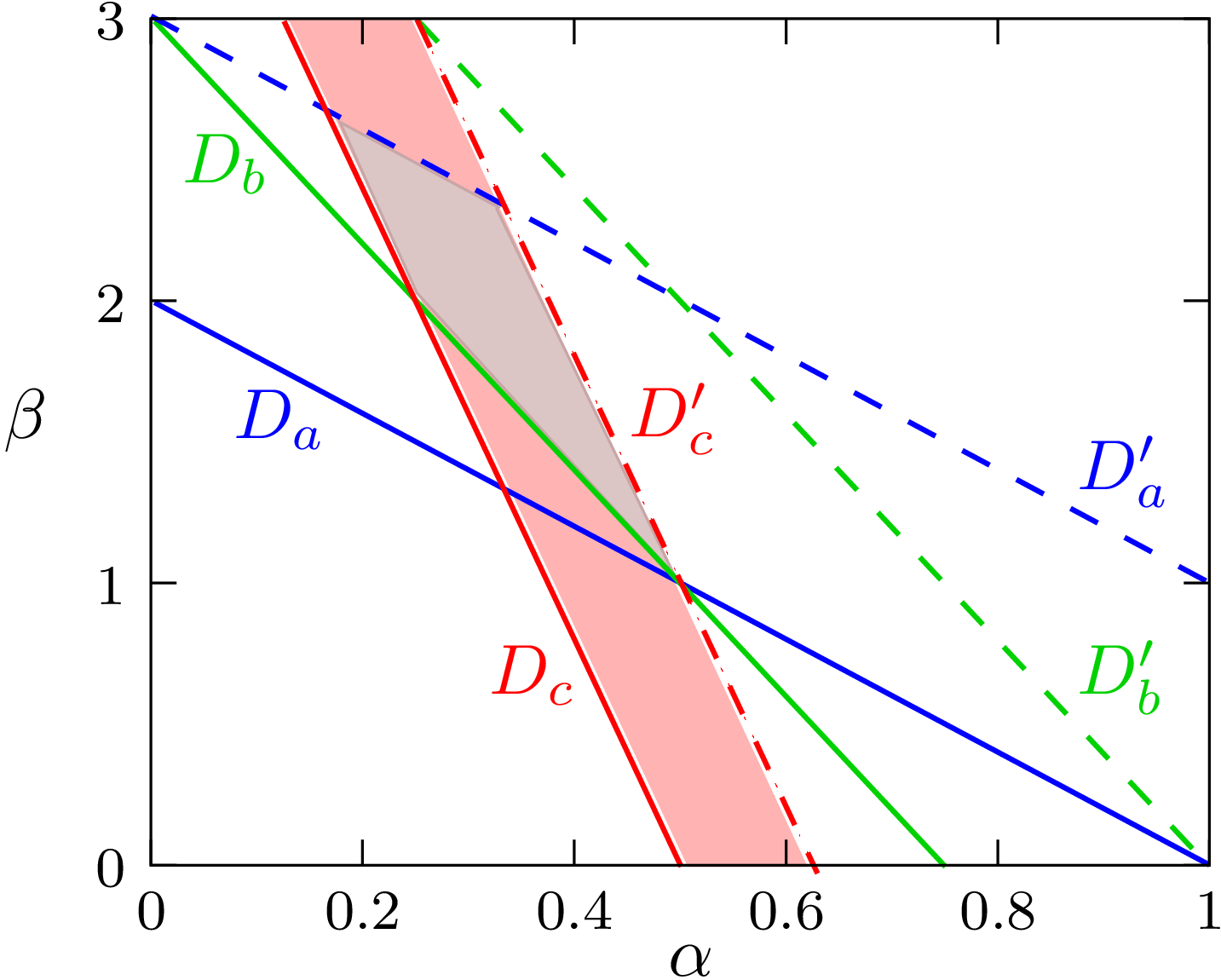
|
 ,
,  and
and 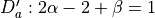
|
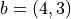 ,
, 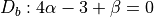 and
and 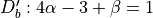
|
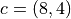 ,
, 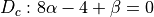 and
and 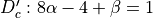
|
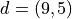 ,
, 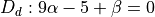 and
and 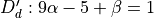
|
 in the dual space leads to
in the dual space leads to 
Preimage = Classical linear programming problem
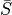 is convex
is convex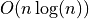 to maintain
to maintain 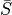 (
(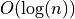 per constraint)
per constraint)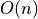
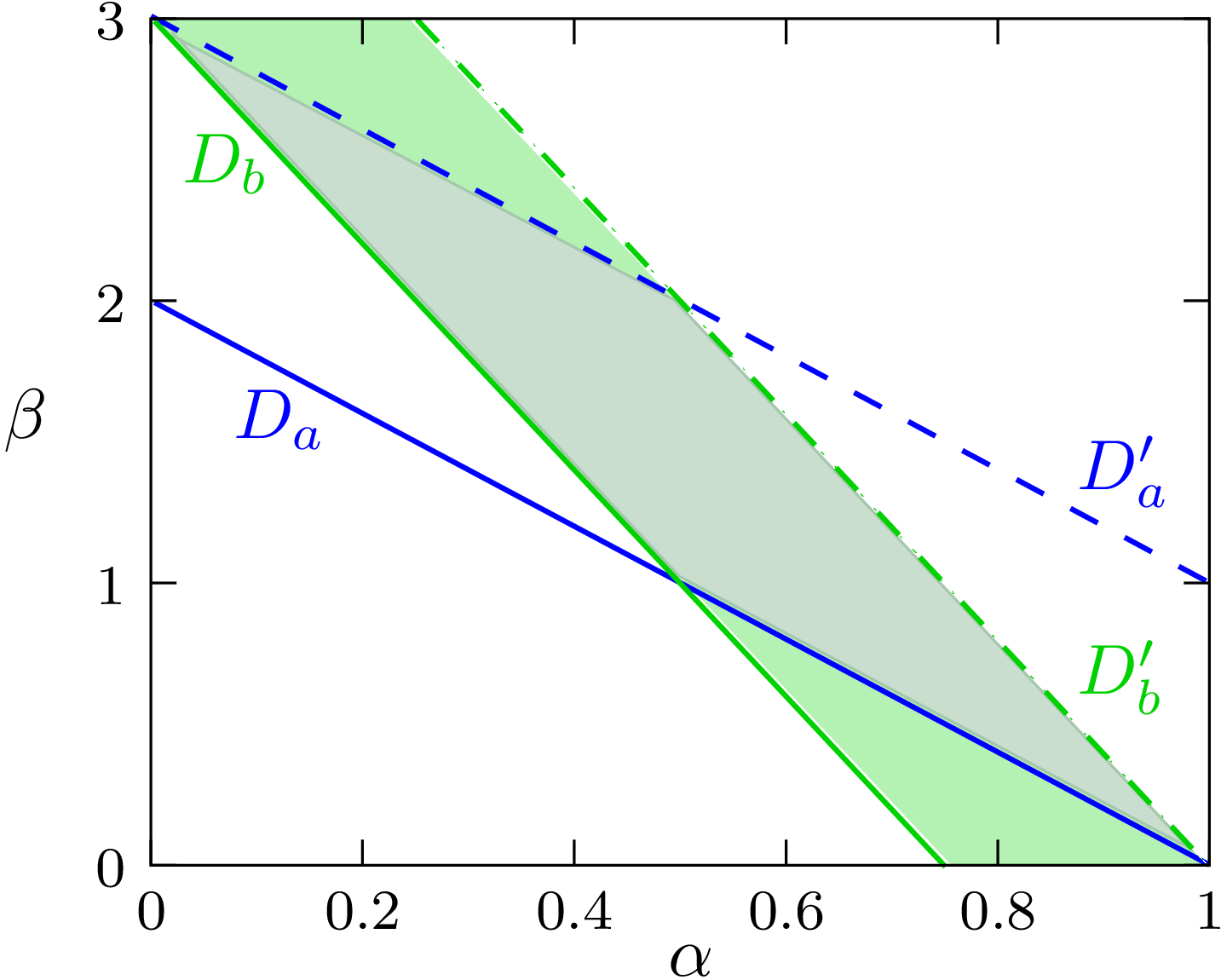
If 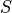 is a (0)-path
is a (0)-path
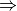 On-line DSS recognition in
On-line DSS recognition in 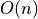 (O(1) per constraint)
(O(1) per constraint)
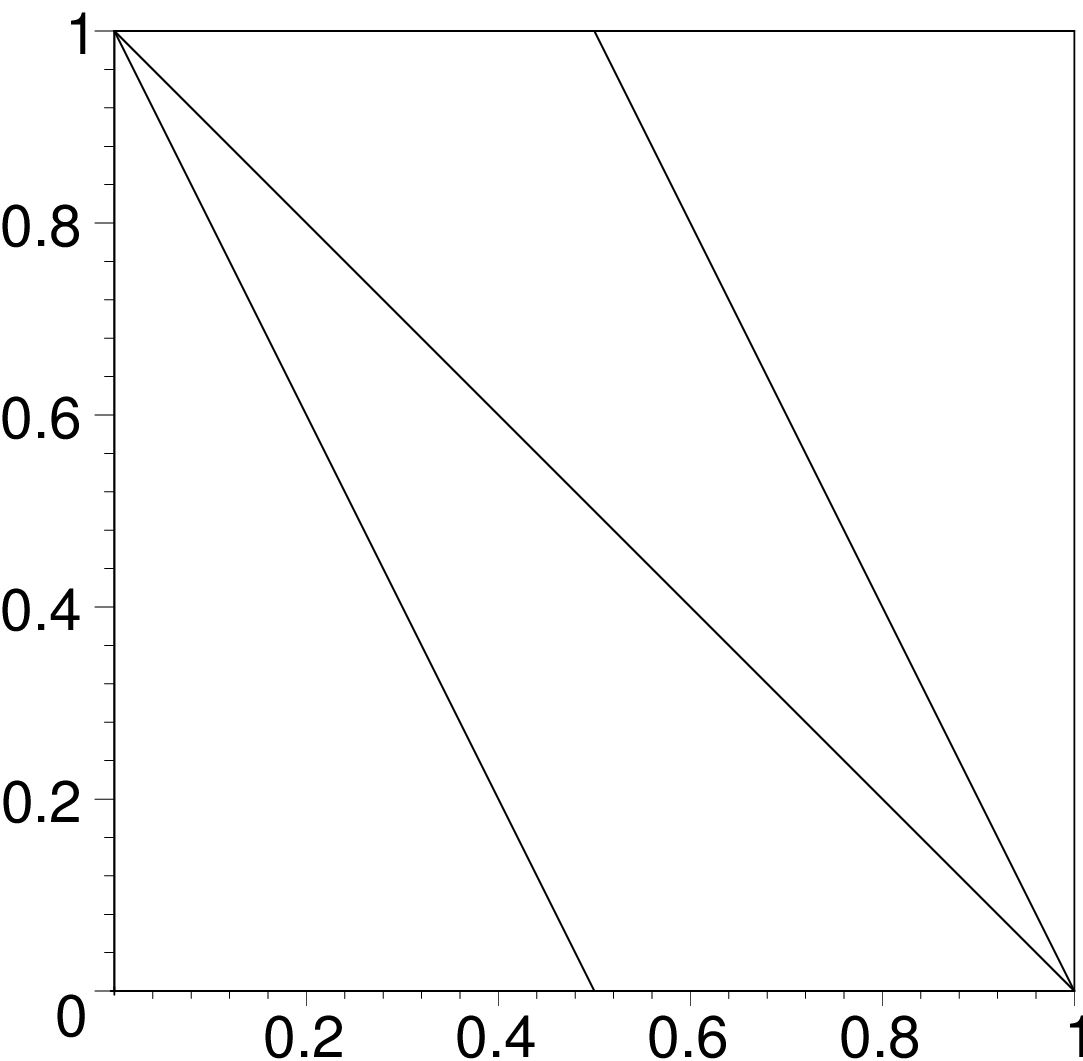
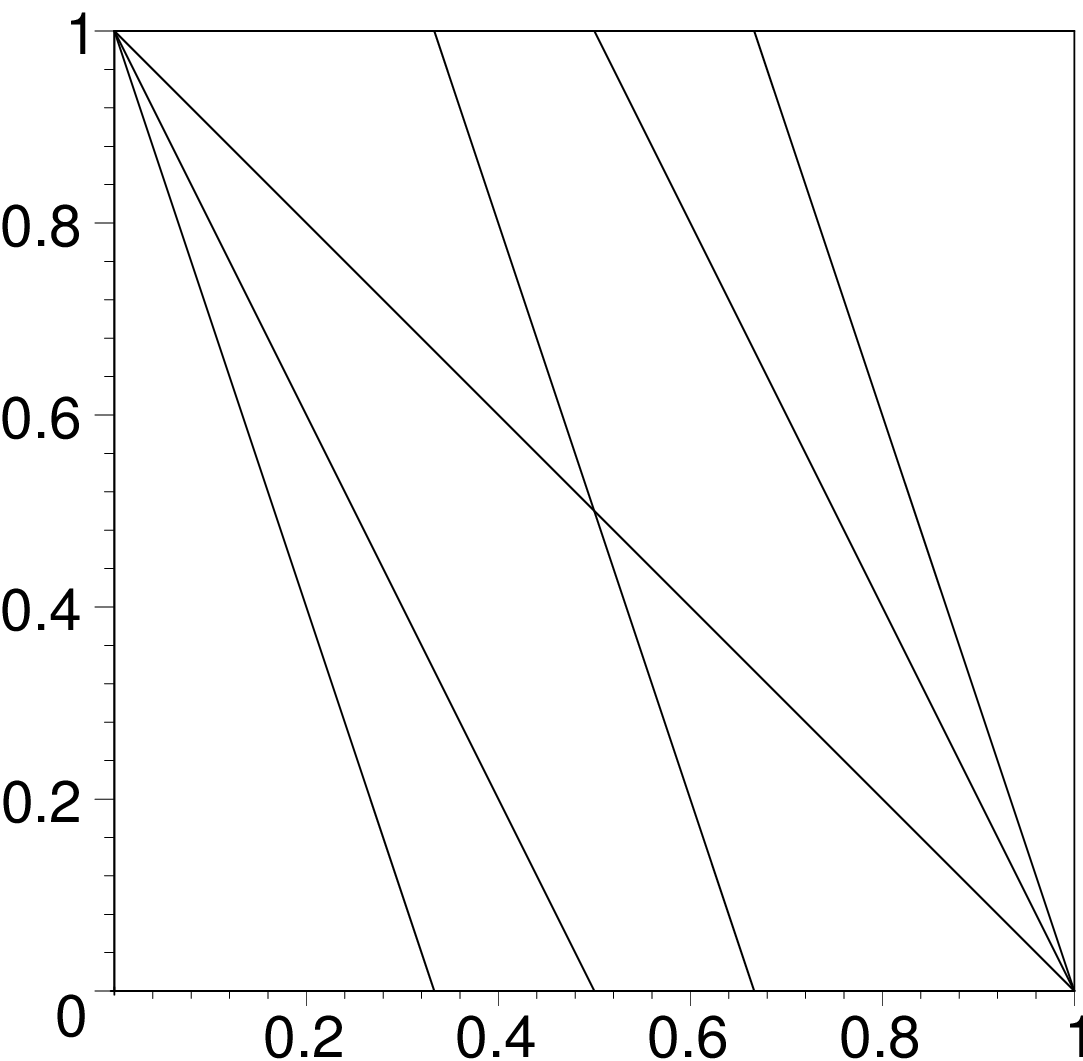
Farey Fan
The Farey Fan of order 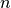 is a decomposition of the space into cells where each cell corresponds to a DSS preimage of length
is a decomposition of the space into cells where each cell corresponds to a DSS preimage of length 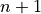
|
|
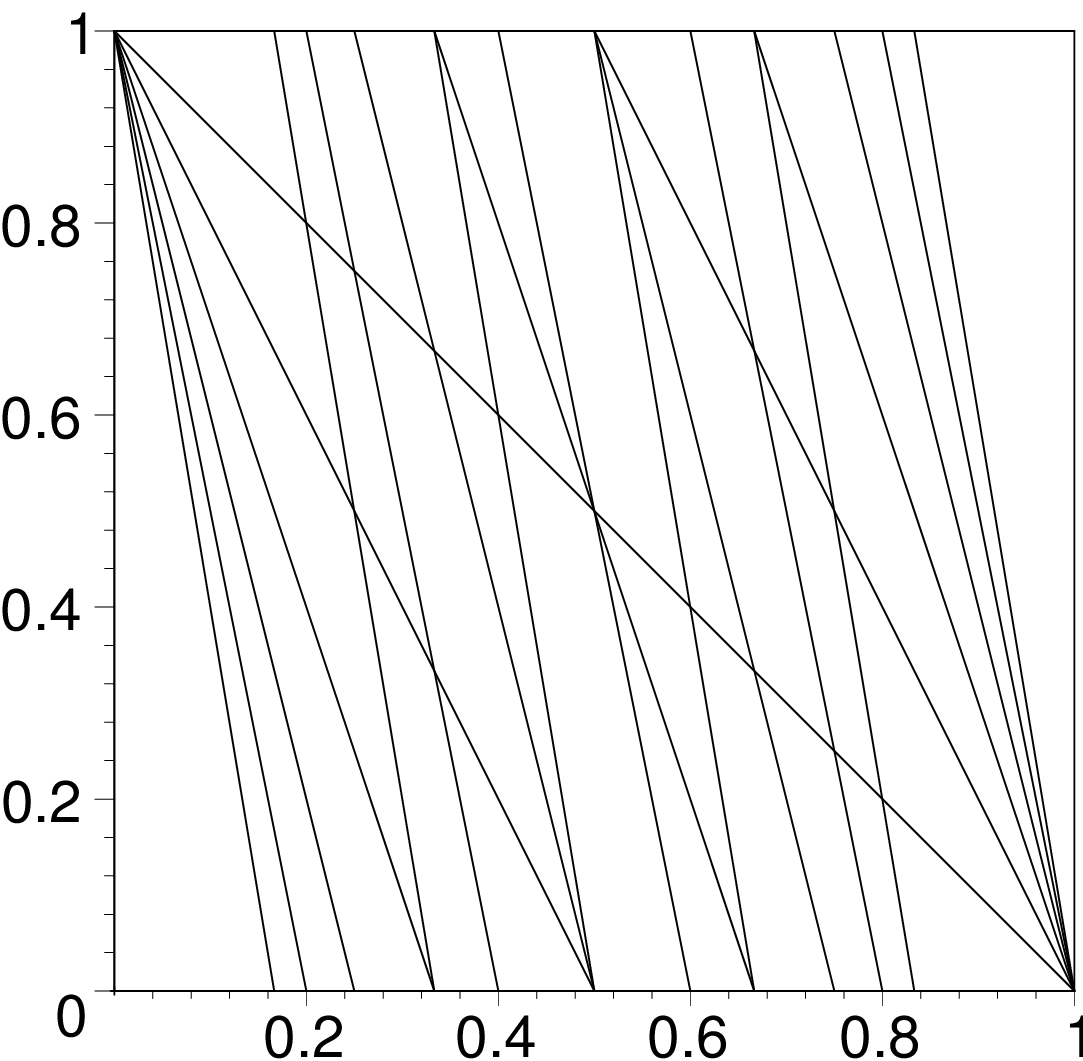
|
| Order 2 | Order 3 | Order 6 |
Idea
Use the analytical representation of DSS:
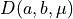 a DSS in the first octant
a DSS in the first octant
the reminder of a pixel 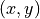 is the quantity
is the quantity
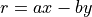
the k-th net is defined by the solutions of
the DSS is the union of nets with 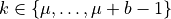
Definitions (again)
Defs.
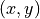 is exterior to D if its reminder is lesser than
is exterior to D if its reminder is lesser than 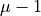 or greater than
or greater than 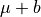
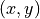 is weakly exterior to D if its reminder is equal to
is weakly exterior to D if its reminder is equal to 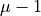 or
or 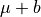
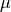 is the upper leaning net
is the upper leaning net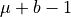 is the lower leaning net
is the lower leaning netLet U (resp. U’) be the upper leaning point with minimal abscissa (maximal abscissa) and L (resp. L’) be the lower leaning point with minimal abscissa (maximal abscissa)
Given a DSS digital set S w and a point M (with reminder r), we have to decide if 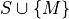 is still a DSS
is still a DSS
Thm.
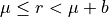 then
then 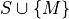 is a DSS with parameter
is a DSS with parameter 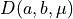
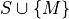 cannot be a DSS
cannot be a DSS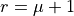 ,
, 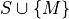 is a DSS where the slope is given by
is a DSS where the slope is given by 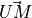
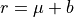 ,
, 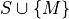 is a DSS where the slope is given by
is a DSS where the slope is given by 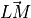
At each step, we maintain/update U,U’,L,L’ and DSS parameters a,b, 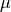
Computational cost
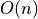 algorithm with
algorithm with 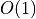 per pixel
per pixelKey point of the proof: unimodular vectors
Given two vectors 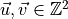 ,
, 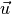 and
and 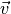 are unimodular iff
are unimodular iff 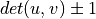
E.g.  and
and 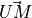 are unimodular if
are unimodular if 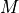 is weakly superior
is weakly superior
(if vectors define fractions, fractions are neighbors in a given Farey series)
Unimodular means that there is no integer point in the parallelogram (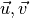 )
)
Similar approaches
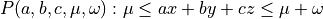 with similar topological results according to
with similar topological results according to  , with similar arithmetical structure (leaning points, unimodular vectors, …)
, with similar arithmetical structure (leaning points, unimodular vectors, …)
|
|
|
| P(6,13,27,0,15) | P(6,13,27,0,27) | P(6,13,27,0,46) |
Digitization -> Constraints
Given the primitive (plan, circle, …), digitization usually implies inequality system we have to solve
Usually:
Regularity/arithmetic in analytical representation
Design the recognition as a separation problem with tools from Computational Geometry
In practice: a kind of mix between all these approaches…
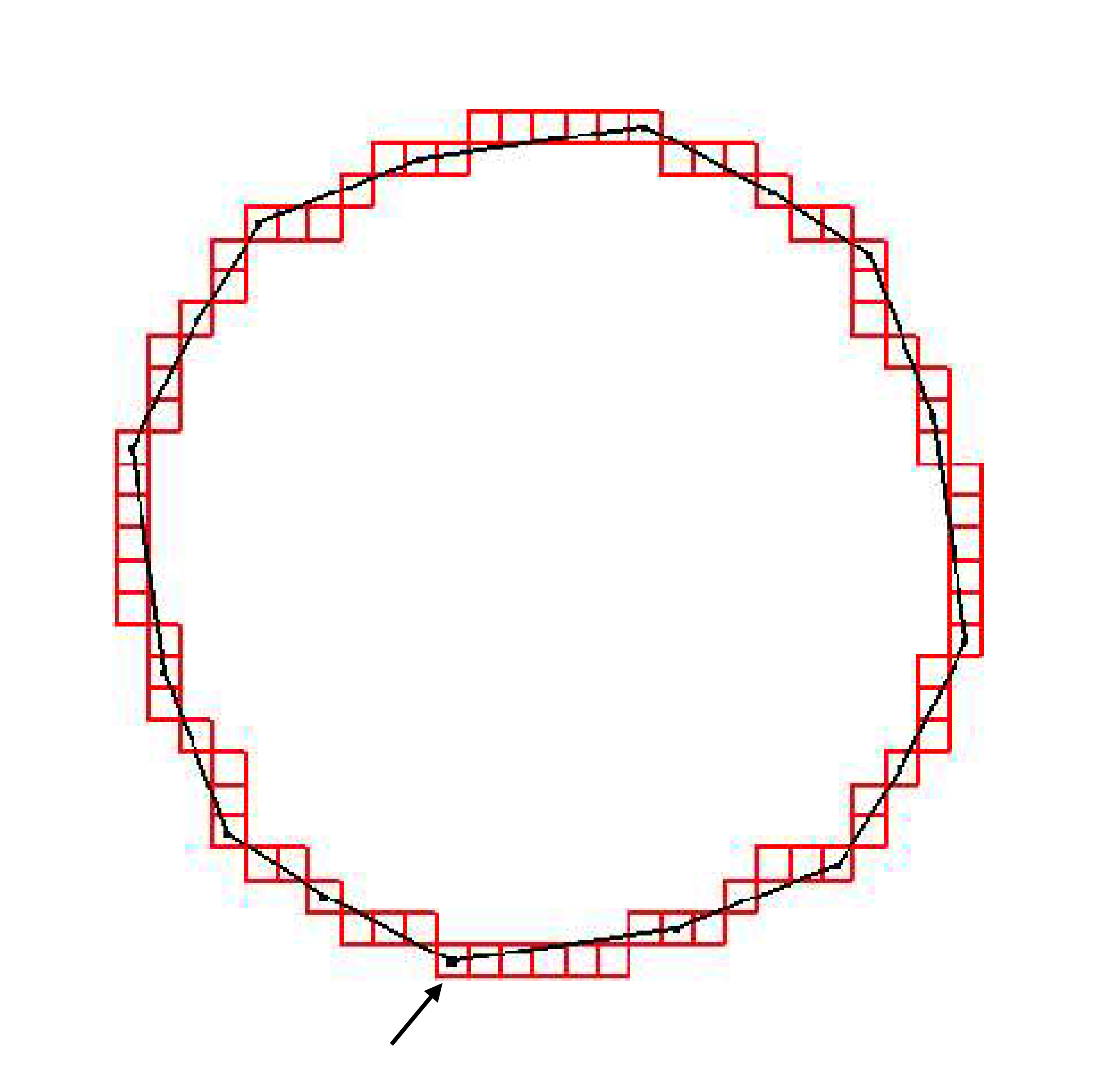
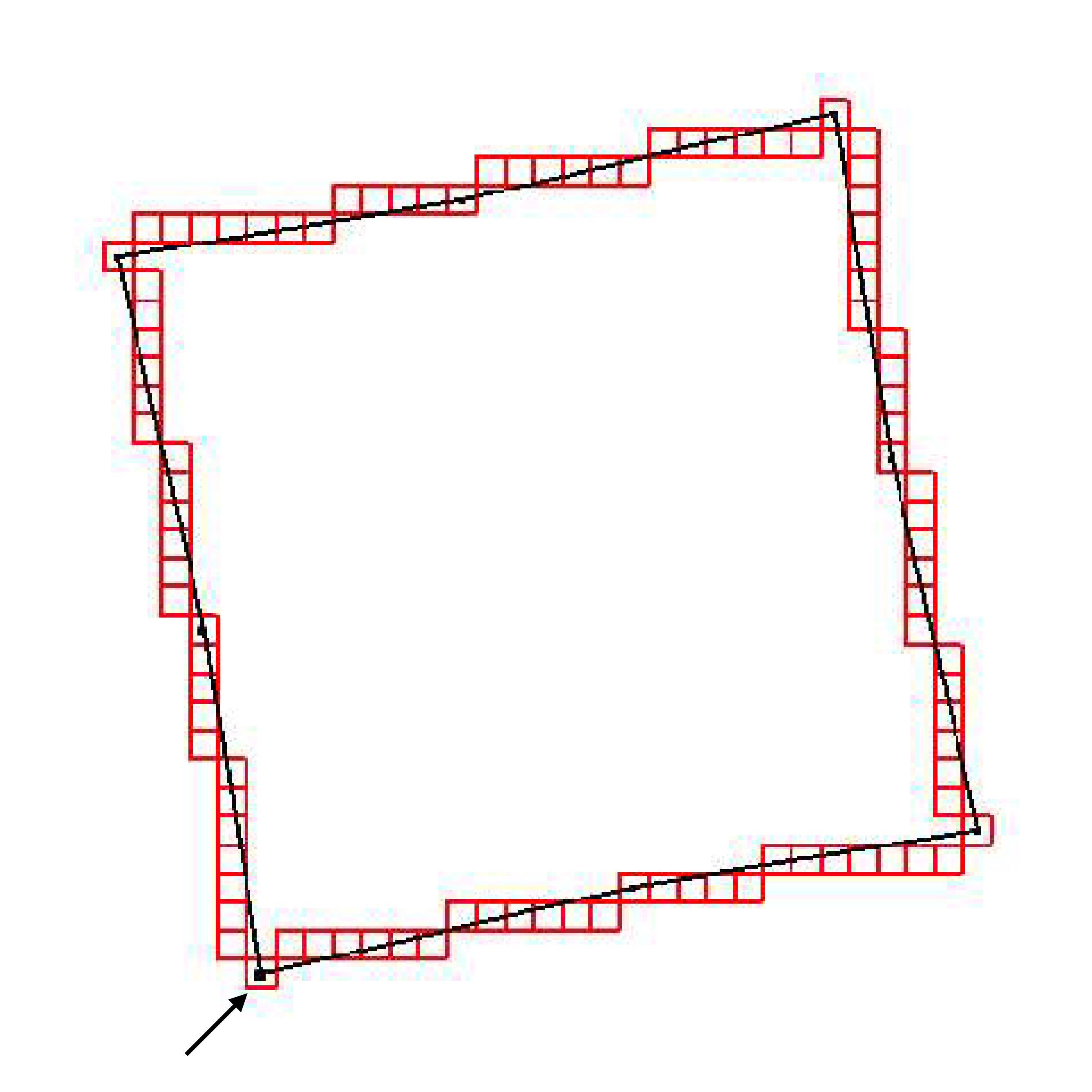
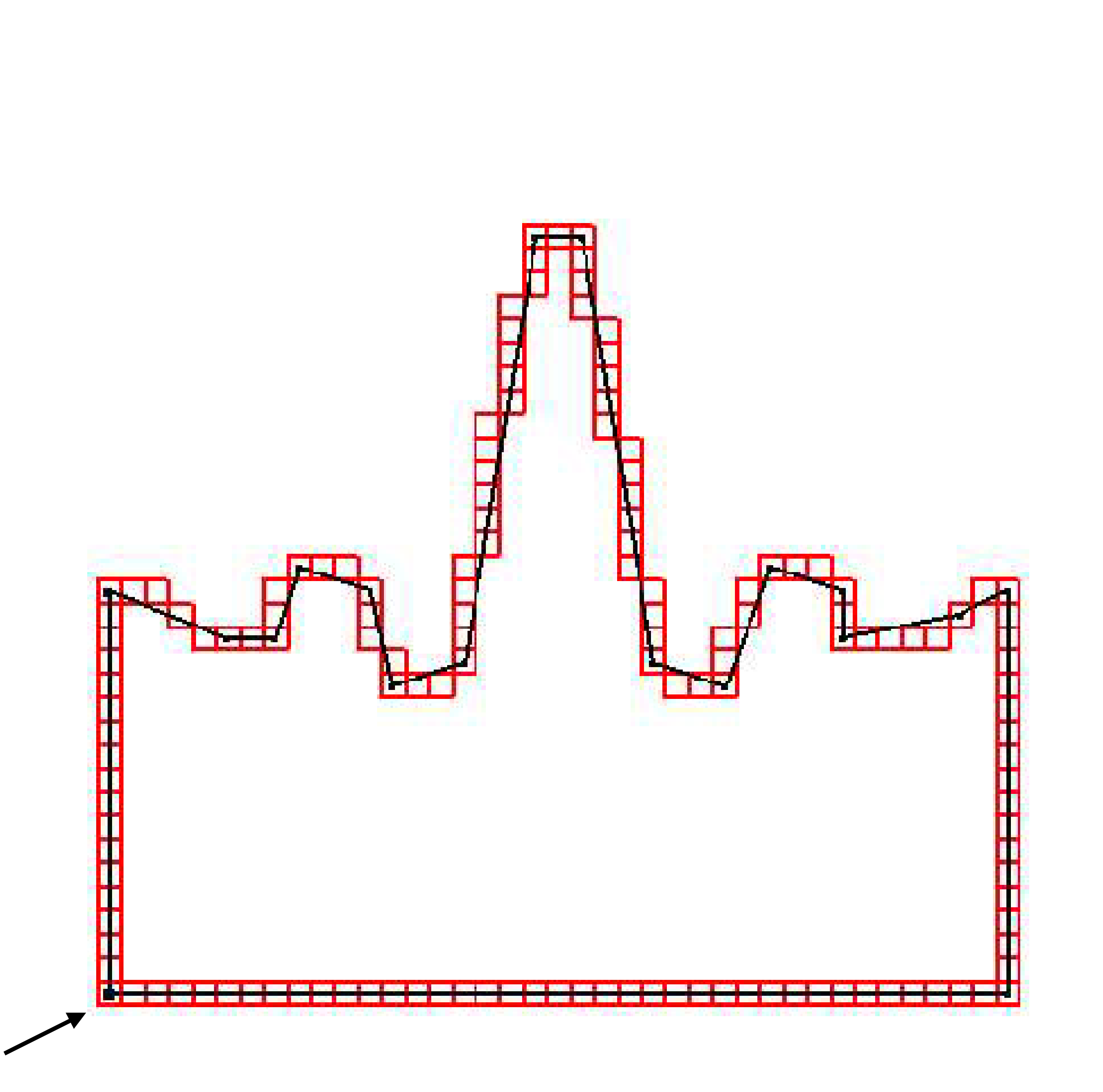
Idea
Starting from a contour point (and given a direction), decompose the contour into maximal DSS adding pixels one by one
|
|
|
 O(n) algorithm
O(n) algorithm
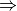 Changing the starting point, decompositions differs by one (N, N+1)
Changing the starting point, decompositions differs by one (N, N+1)
Similar approach but
Usually

|

|
Principle
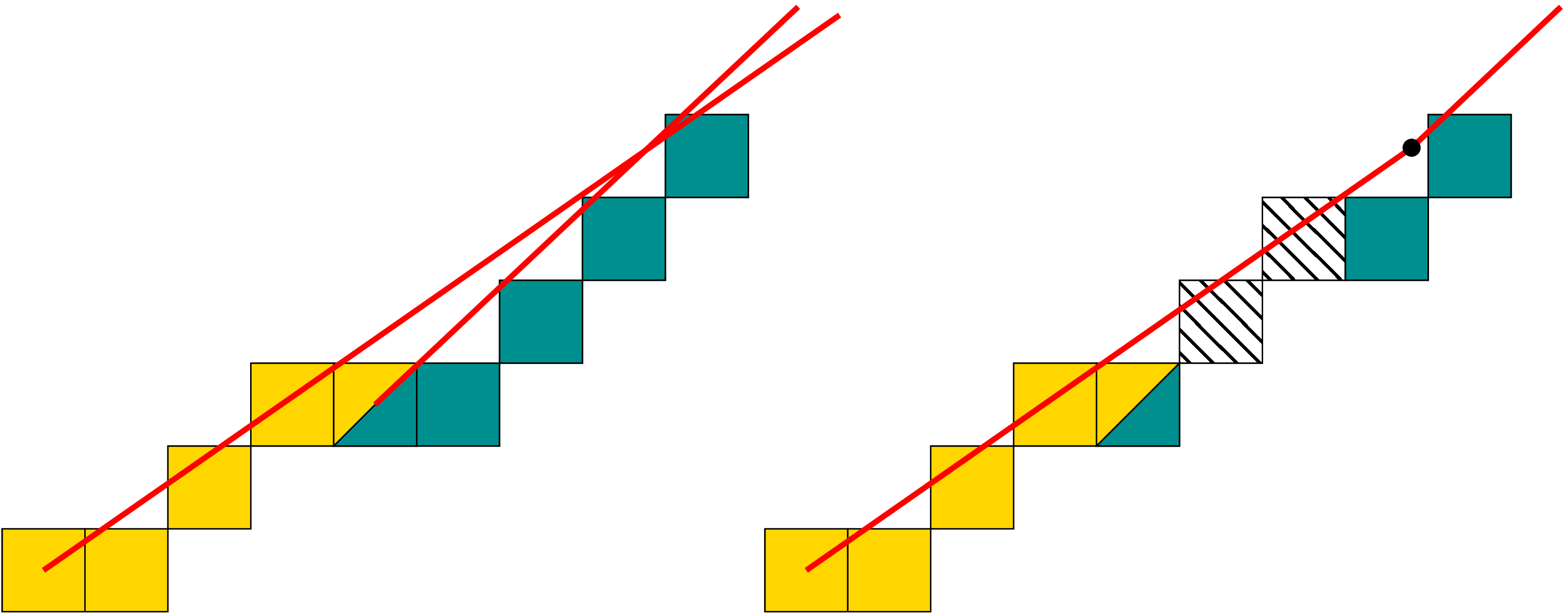
Convert a digital contour into a polygon such that its digitization is the input digital set
First approach: use DSS decomposition
Indeed, DSS segments are “reversible” … but not the vertices..
|
|
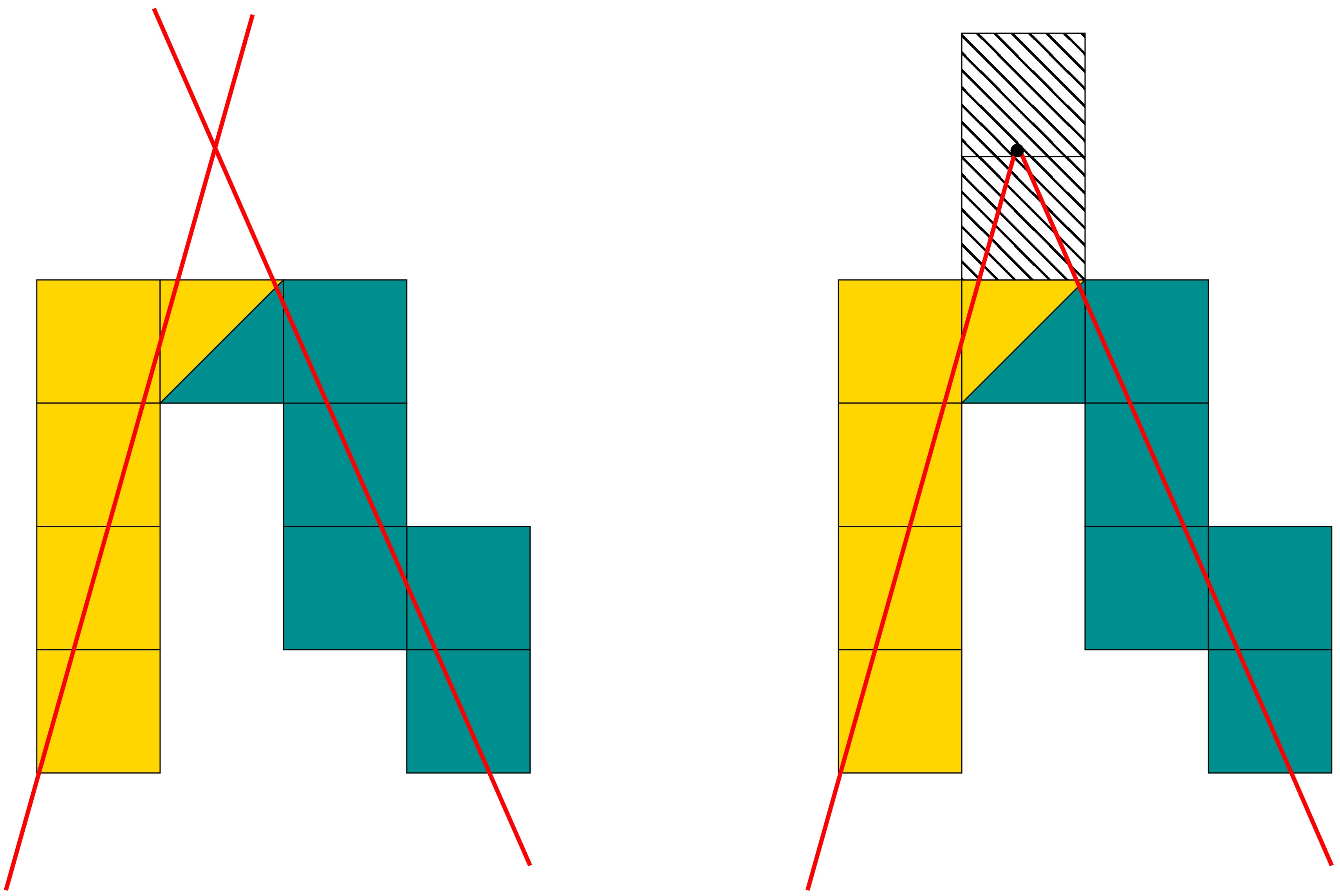
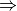 We need to constraint the preimages to ensure that successive DSSs have euclidean representative segment with “reversible” intersection vertex
We need to constraint the preimages to ensure that successive DSSs have euclidean representative segment with “reversible” intersection vertex
More difficult because of topological issues.
Idea: start from a topologically valid reversible triangulation (Marching Cubes), merge triangles using digital plane decomposition information and constraints on preimage