Digital Geometry: Volumetric Analysis§
| author: | David Coeurjolly |
|---|
| author: | David Coeurjolly |
|---|
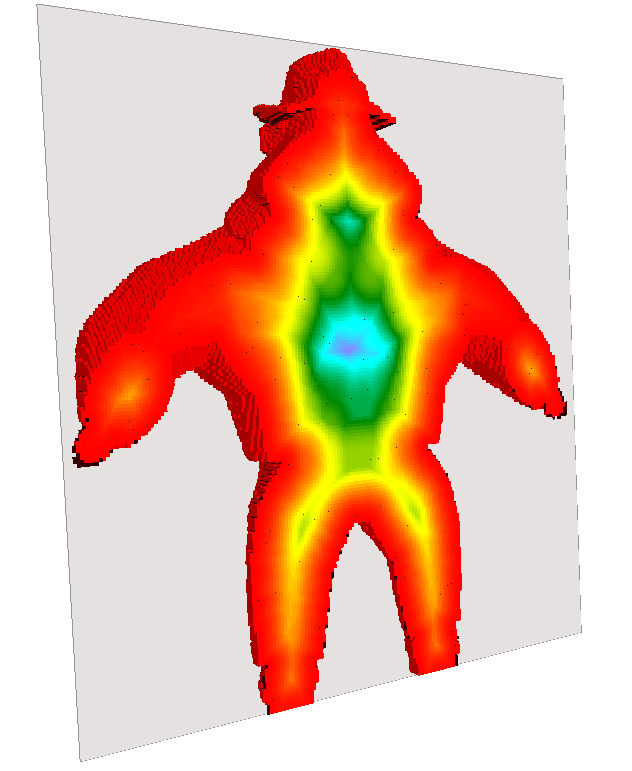
Distance transformation
Def.
At each point 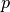 of a shape
of a shape 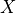 , we want the smallest distance to
, we want the smallest distance to 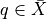

|

|

|
 We need
We need
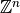
Very usefull
…for many applications

|

|

|
Idea
Shape  Boundary
Boundary  Distance field
Distance field  Implicit representation
Implicit representation 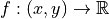
Objectives
 DT)
DT)
|

|
|
Objectives
 DT)
DT)
|

|
Def.
Metric 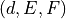 is a map
is a map 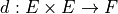 such that
such that
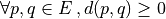 (separation axiom)
(separation axiom)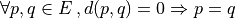 (coincidence axiom)
(coincidence axiom)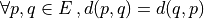 (symmetry)
(symmetry)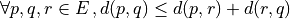 (triangular inequality)
(triangular inequality)Def.
 is a norm (metric induced by “normed” vector space) iff
is a norm (metric induced by “normed” vector space) iff
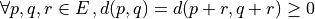 (translation invariant)
(translation invariant)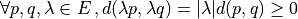 (homogeneity)
(homogeneity)E.g.
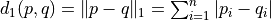
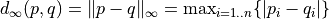
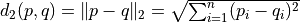
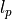 metric:
metric: 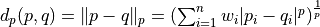

Definition
Hence
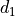 ,
, 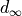 are Discrete Metrics
are Discrete Metrics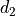 is not a discrete metric
is not a discrete metric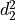 is not a metric
is not a metric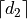 is a discrete metric
is a discrete metric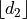 is a not discrete metric
is a not discrete metric![[d_2]](_images/math/cead7f2a8fdc71f0fdcf6aad89394bc45b4a1fb4.png) is not a metric
is not a metricHints for last two results use 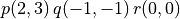 and
and 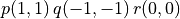
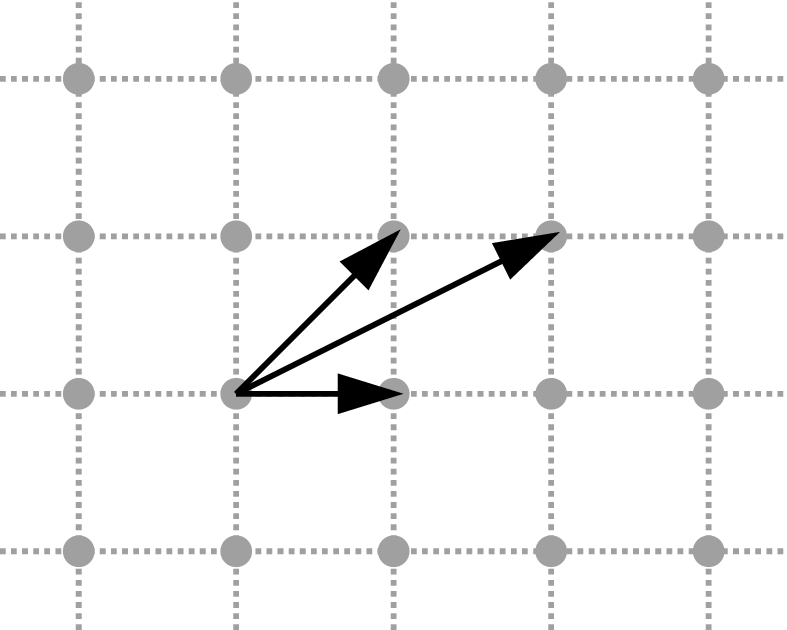
Weigthed vector
Chamfer Mask
Set of weighted vector
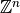
Usually, chamfer masks are G-symmetric, i.e. restricted to
with
Chamfer path
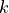 -Path based on vectors from a chamfer mask
-Path based on vectors from a chamfer mask
Length of a chamfer path
Chamfer distance
Minimal length of chamfer path between
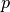 and
and
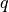
All chamfer distances induced distances, not necessarily norm
Path based distance
Matrix representation for masks
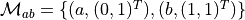 ,
, 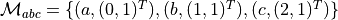
For example:
(distances must be divided by 3 at the end)
 We need constraints on
We need constraints on 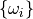 to induce norms
to induce norms
e.g.
We construct the mask to approximate the Euclidean Metric
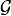 )
)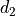 on specific configuration
on specific configuration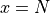
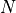
Drawbacks
Propagation using Dijkstra’s algorithm
 vertices and edges taken from
vertices and edges taken from 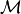
 Computation cost in
Computation cost in 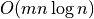 for
for 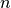 grid points and
grid points and 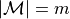

|
|
|
Split the mask into two sub-masks and perform forward/backward scans with “min” operations.
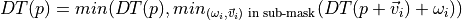
 Computational cost in
Computational cost in 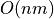
Neighborhood sequence
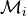
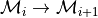
Example
“Octogonal” distance with infinite sequence 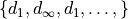
Sometimes, explicit forms exist
Idea
Still consider 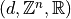 distances but with integer based representations and algorithmic
distances but with integer based representations and algorithmic
E.g.
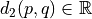 by
by 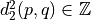
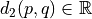 by vector
by vector 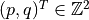
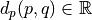 by
by 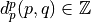 or even
or even 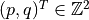 for
for 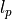 metrics
metricsNice but are there fast algorithms for such exact metrics ?
We want to compute (for all 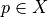 )
)
Separable approach with intermediate map
in dimension 3, we would have
Simple two-scan propagation

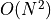 in 2D for NxN image
in 2D for NxN image

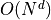 in d-D for N^d image
in d-D for N^d image
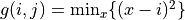 and
and 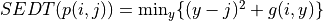
Key-point Lower envelope computation of a set of parabolas
Consider the set of parabolas 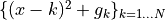
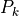 and
and 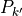 are two parabolas with intersection
are two parabolas with intersection 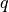 and
and 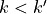
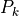 cannot appear in the lower envelope for abscissa greater than
cannot appear in the lower envelope for abscissa greater than 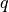
 Lower envelope computation in
Lower envelope computation in 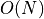 using stack based approach ;)
using stack based approach ;)
Given a 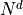 image
image
Algorithm
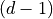 remaining dimensions: compute independent lower envelope which are in
remaining dimensions: compute independent lower envelope which are in 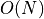
 algorithm for error free Euclidean metric DT
algorithm for error free Euclidean metric DT
|
|
Thanks to separability
Optimal multi-thread implementation
Generalization to toric domains
Useful to characterize periodic structures in arbitrary dimensions
Principle
Def.
We consider 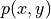 ,
, 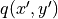 with
with 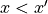
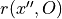 be a point on the x-axis such that
be a point on the x-axis such that 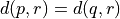
Let 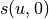 be another point on the x-axis
A metric
be another point on the x-axis
A metric 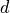 is monotonic if
is monotonic if
Result
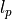 metrics are monotonic
metrics are monotonic Let’s use the separable approach for other metrics !
Let’s use the separable approach for other metrics !
Definition
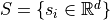 , the Voronoi Diagram is a decomposition of the space into closed cells
, the Voronoi Diagram is a decomposition of the space into closed cells 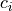 such that
such that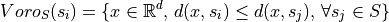
Each cell can be further decomposed into sub-dimensional i-facets taking into account cases where 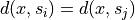
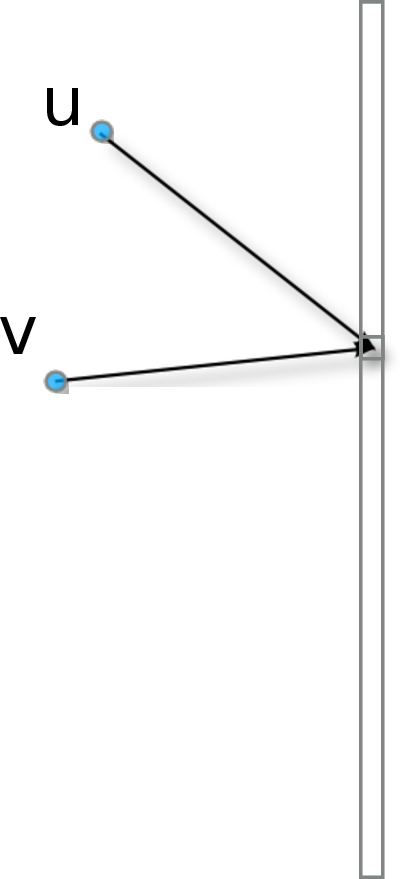
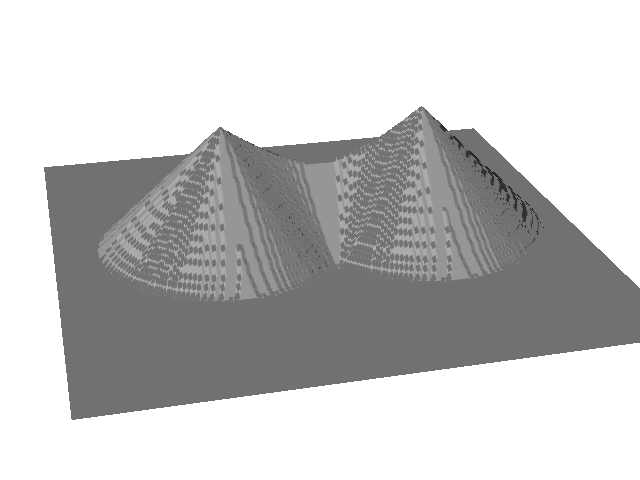
Voronoi Diagram  Distance Transformation
Distance Transformation
 Getting the distance value is equivalent to localizing a point in a Voronoi diagram
Getting the distance value is equivalent to localizing a point in a Voronoi diagram
Input set: 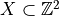 , we construct
, we construct 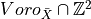
Main Result
For any monotonic metric and an image ![[1\ldots n]^d\rightarrow \{0,1\}](_images/math/1320afc9a136676702fdf76c54f4309d526ff1b7.png) , the Voronoi Map (and the distance transformation) can be obtained by the separable algorithm in , the Voronoi Map (and the distance transformation) can be obtained by the separable algorithm in 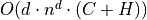 |
|
|
| Metric | C | H | Total |
|---|---|---|---|
 |
 |
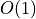 |
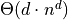 |
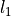 |
 |
 |
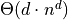 |
 |
 |
 |
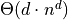 |
Exact 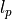 |
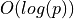 |
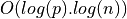 |
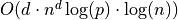 |
| Chamfer Norms | 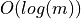 |
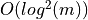 |
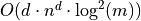 |
| Neigh. Seq. Norms | O(1) | 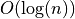 |
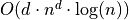 |
Better expected bounds for path based norms
| Metric | C | H | Total |
|---|---|---|---|
| Chamfer with adapter | 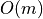 |
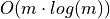 |
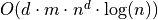 |
| Chamfer Norms | 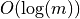 |
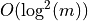 |
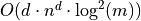 |
Similar expected results for neighborhood sequences
Notations
Chamfer masks: 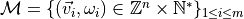 (we consider only chamfer masks inducing norms)
(we consider only chamfer masks inducing norms)
Rational ball: 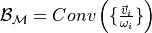 [Normand, Strand,…]
[Normand, Strand,…]
Rational ball faces have normal vector 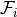
[Normand et al.]

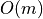
Can be generalized to other path based distances to get similar expression
for some function 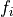 (based Lambek-Moser inverse sequences)
(based Lambek-Moser inverse sequences)
Computational Geometry setting
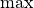 is given by the facet pierced by the straight line
is given by the facet pierced by the straight line 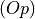
 Ray shooting problem in convex polytopes
Ray shooting problem in convex polytopesFast Distance computation
Following [Matousek and Schwarzkpof]
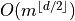 space/pre-processing and
space/pre-processing and
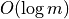 per query
per query
Goal
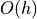 then we have exact Voronoi Map/DT in
then we have exact Voronoi Map/DT in 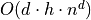
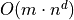
Main Result
==> First sub-quadratic DT algorithm for Chamfer metrics
Key point
Given to points and a straight line, detect the position of the Voronoi edge on the line
we are looking for point 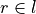 such that
such that 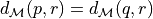
Question Find the cone at 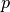 containing a point
containing a point 
==> Dichotomic/Binary search (thanks to convexity of the metric)
==> 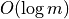
Idea
If we have localized the Voronoi edge point, we are done (find the exact position given by linear system with one unknown)
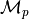 §
§ShrinkMp( Mp, Mq )
if |Mp| == 1
return the cone in Mp
else
Split cones Mp -> { Mp, cone, M-} with |M+|~|M-|
{v1,v2} = cone
dp1 = distance d_M(p, v1 intersection l) //O(1)
dp2 = distance d_M(p, v1 intersection l) //O(1)
dq1 = localize and get the distance of d_M(q, v1 intersection l) //O(log(m))
dq2 = localize and get the distance of d_M(q, v2 intersection l) //O(log(m))
c1 = closest point between p and q at v1
c2 = closest point between p and q at v2
if (c1 == c2 == GREEN)
return ShrinkMp(M+)
if (c1 == c2 == BLUE)
return ShrinkMp(M-)
return cone
Correctness
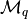 and final computation§
and final computation§Shrinking 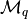
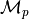 cone
cone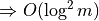
Final step
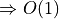
Basic Idea for 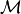 in
in 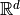
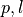
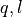 defines a plane (
defines a plane (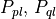 )
)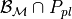 induces a 2-dimensional polytope
induces a 2-dimensional polytope 2D problem with
2D problem with 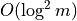 computational cost
computational costConclusion
Closest() and HiddenBy() predicates can be implemented in 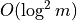
Exact Voronoi map/Distance transformation of Chamfer norms using separable approach in
Problem setting
Def.
Given a metric 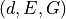 and a set of balls
and a set of balls 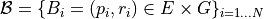 , reconstruct the binary shape
, reconstruct the binary shape 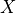
Why?
Reverse operation of the Distance Transformation
To reconstruct the shape 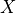 if we characterize it as a union of balls (e.g. via medial axis)
if we characterize it as a union of balls (e.g. via medial axis)
Bruteforce approach
For 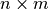 image
image
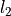 §
§W.l.o.g. we consider 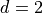
Let us denote 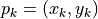 for
for 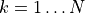 , then
, then
Which can be rewritten
 Separable decomposition
Separable decomposition
Start from a map 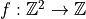 with
with 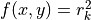 if
if 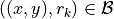 (
(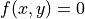 otherwise)
otherwise)
Similar algorithm
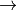 Upper envelope computation of a set of parabolas
Upper envelope computation of a set of parabolas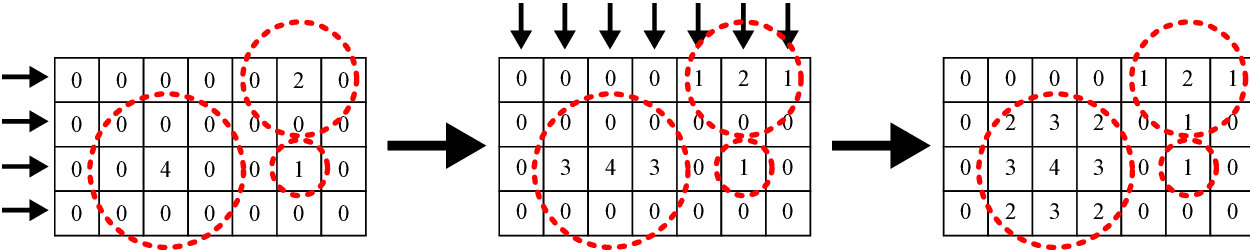

 separable algorithm for REDT
separable algorithm for REDT
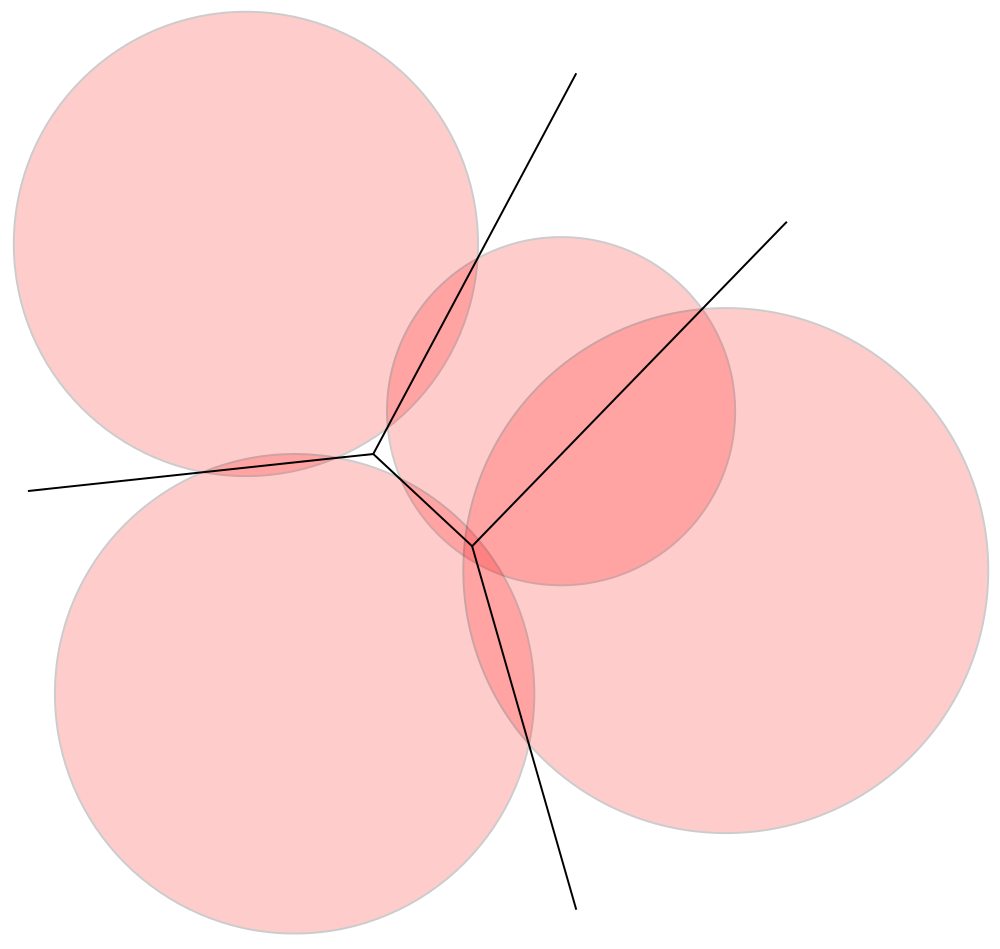
Voronoi map –> Power map
Kind of Voronoi diagram with additive power metric. For example the power of a point x w.r.t. ball 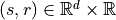
Def.
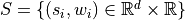 , the Power Diagram is a decomposition of the space into closed cells
, the Power Diagram is a decomposition of the space into closed cells 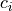 such that
such that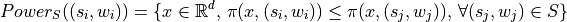
Each cell can be further decomposed into sub-dimensional i-facets taking into account cases where 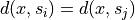
|

|
Idea
 is equivalent to the construction of
is equivalent to the construction of 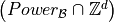
Results
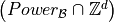
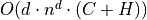 computational cost for a large class of metrics
computational cost for a large class of metricsAlternative Definitions
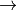 PDE fromulation)
PDE fromulation) is maximal in X if
is maximal in X if 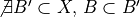
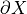 at least twice
at least twice
|
|
Voronoi Based Approximation
Shape
 Point set approximation
Point set approximation
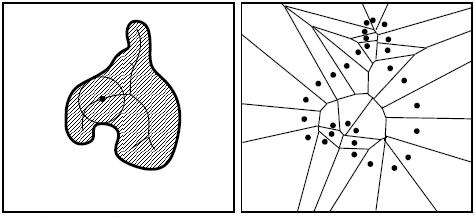
 Voronoi Diagram
Voronoi Diagram
 Medial Axis approximation
Medial Axis approximation
Convergence results exists for various classes of Voronoi based medial axis
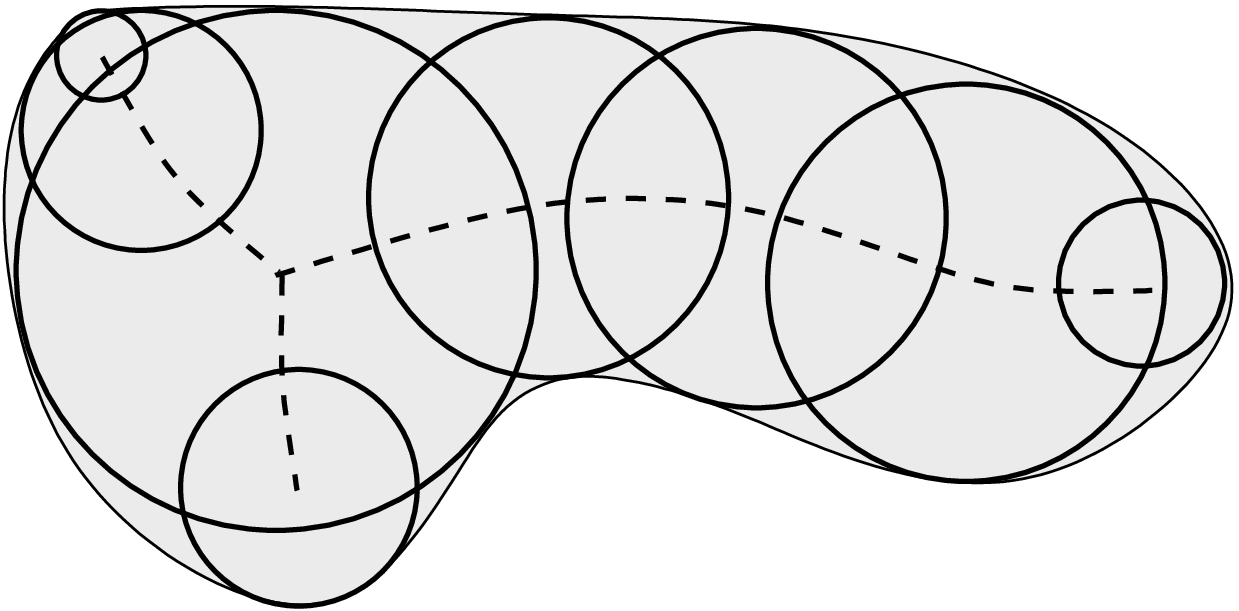
Def.
A maximal ball is a ball contained in the shape not entirely covered by another ball contained in the shape
Def.
The medial axis of a shape is the set of maximal ball centers contained in the shape.
Digital Setting
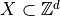
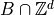
 Finite set of digital balls contained in
Finite set of digital balls contained in 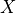
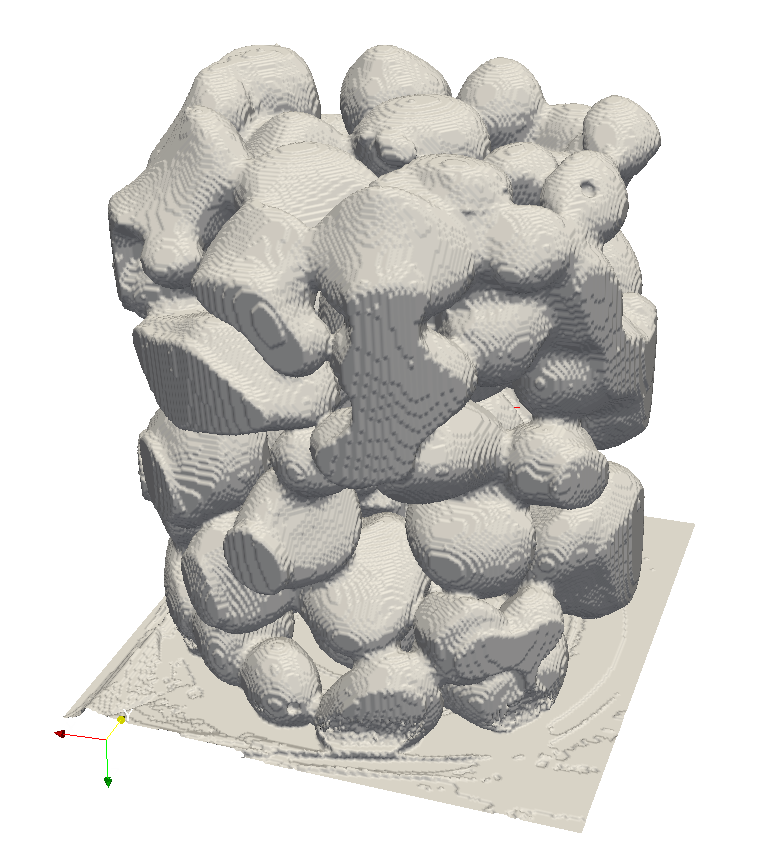
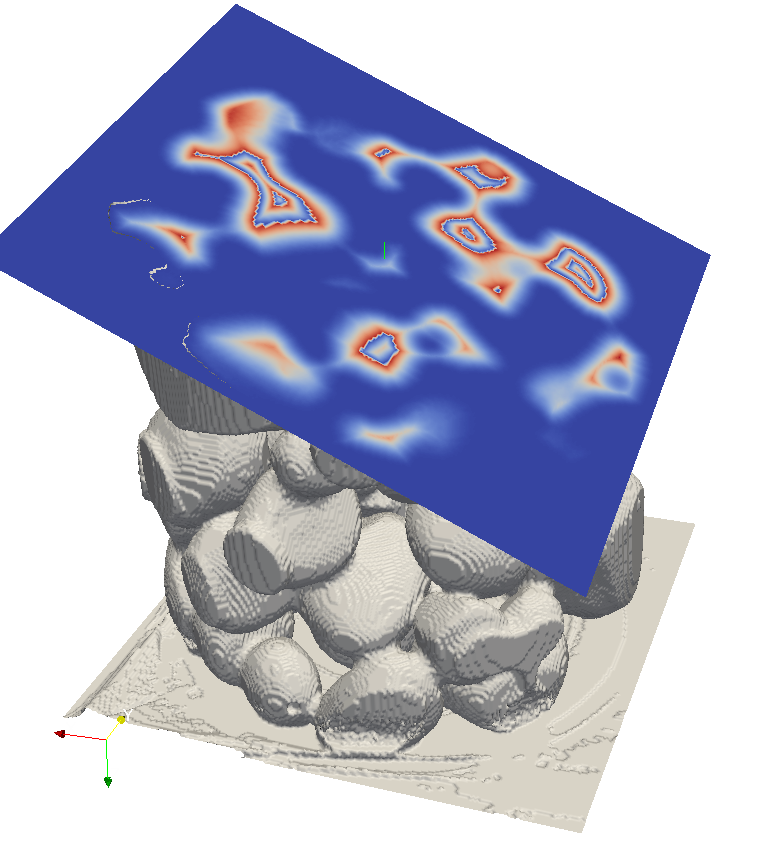
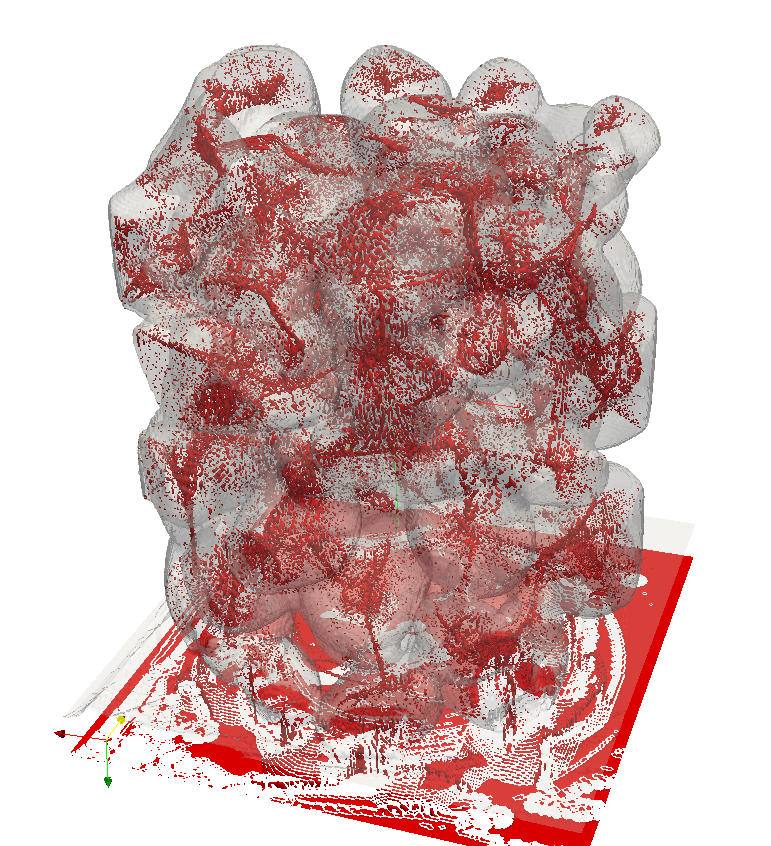
 Medial Axis Extraction
Medial Axis Extraction  Combinatorial Covering problem
Combinatorial Covering problemReversible Encoding of X
DT as preliminary step
Given 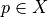 and
and 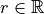 such that Euclidean ball with
such that Euclidean ball with 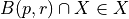 , we have
, we have
(defined for 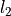 but trivial generalizations to other metrics)
but trivial generalizations to other metrics)
|
|
|
 Set of candidate balls
Set of candidate balls 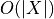
Covering Test
Let us consider a IsCoveredBy(B,B’) a predicate returning true if 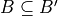
If B and B’ are Euclidean balls  The predicate is in
The predicate is in 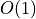
If B and B’ are Digital balls  The predicate is in
The predicate is in 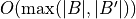

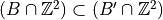
but
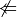
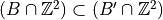
 Bruteforce Digital Medial Axis Extraction
Bruteforce Digital Medial Axis Extraction 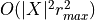 (with
(with 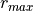 the maximal DT value)
the maximal DT value)
Goal
Design a IsCoveredBy() predicate with cost as a function of 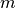
Elementary Chamfer Masks 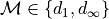
Also true for 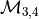 with the following rewriting rules of the DT map:
with the following rewriting rules of the DT map:
Other path-based distances: Look-up table approach
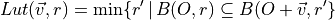
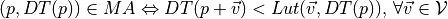
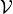 is the neighborhood test.
is the neighborhood test.
Bottlenecks Efficient computation of Lut, bounds on 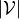 , bounds on
, bounds on 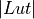 , …
, …
Idea
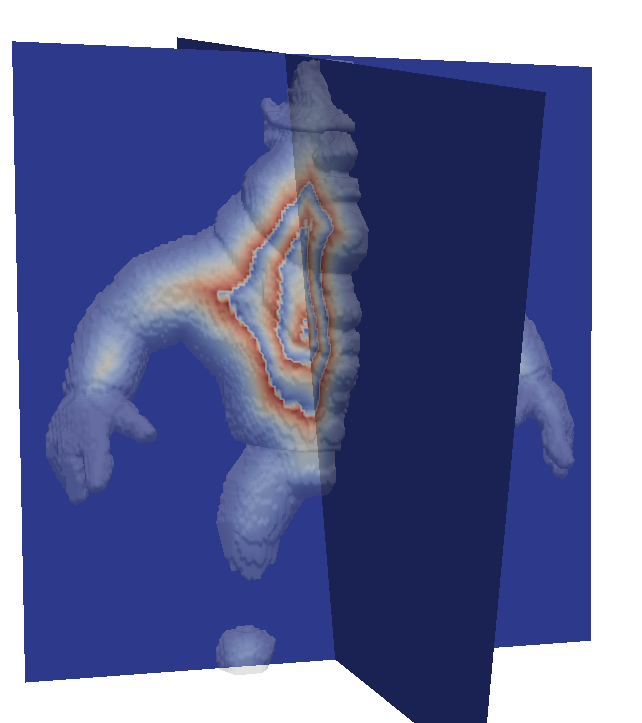
Get the Medial Axis as a by-product of the Power map
Lemma
Let 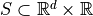 and
and 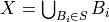
Non-empty power map cells are related to maximal balls
[Skipping details…]
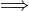 Separable algorithm to extract the medial axis
Separable algorithm to extract the medial axis
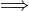
 computational cost for a large class of metrics
computational cost for a large class of metrics

|
|

|
|
|
|
Question
Is the set of maximal balls a minimal representation of X as union of balls ?
Answer No
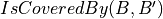
Toward minimal MA
Thm.
If we allow k-ary predicates 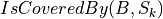 with
with
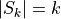 the minimal medial axis problem becomes
NP-complete
the minimal medial axis problem becomes
NP-complete
Digital Medial Axis is defined as a set of balls without any topological information
We are thus looking for
 Iterative thinning via Simple Point Removal
Iterative thinning via Simple Point Removal
Def.
A point 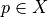 is simple for
is simple for 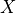 if
if 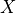 and
and 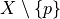 are in the same homotopy equivalence class
are in the same homotopy equivalence class
From Simple Point Definition
Let 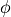 by any sequence of insertions/removals of simple points, then
by any sequence of insertions/removals of simple points, then 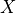 and
and 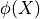 are in the same homotopy equivalence class
are in the same homotopy equivalence class

How to characterize simple points ?
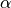 -simple points§
-simple points§Definition
Def.
A point 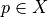 is
is 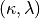 -simple for
-simple for 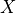 if
if
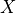 and
and 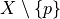 have the same number of
have the same number of  -components
-components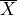 and
and 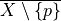 have the same number of
have the same number of  -components
-componentsExample
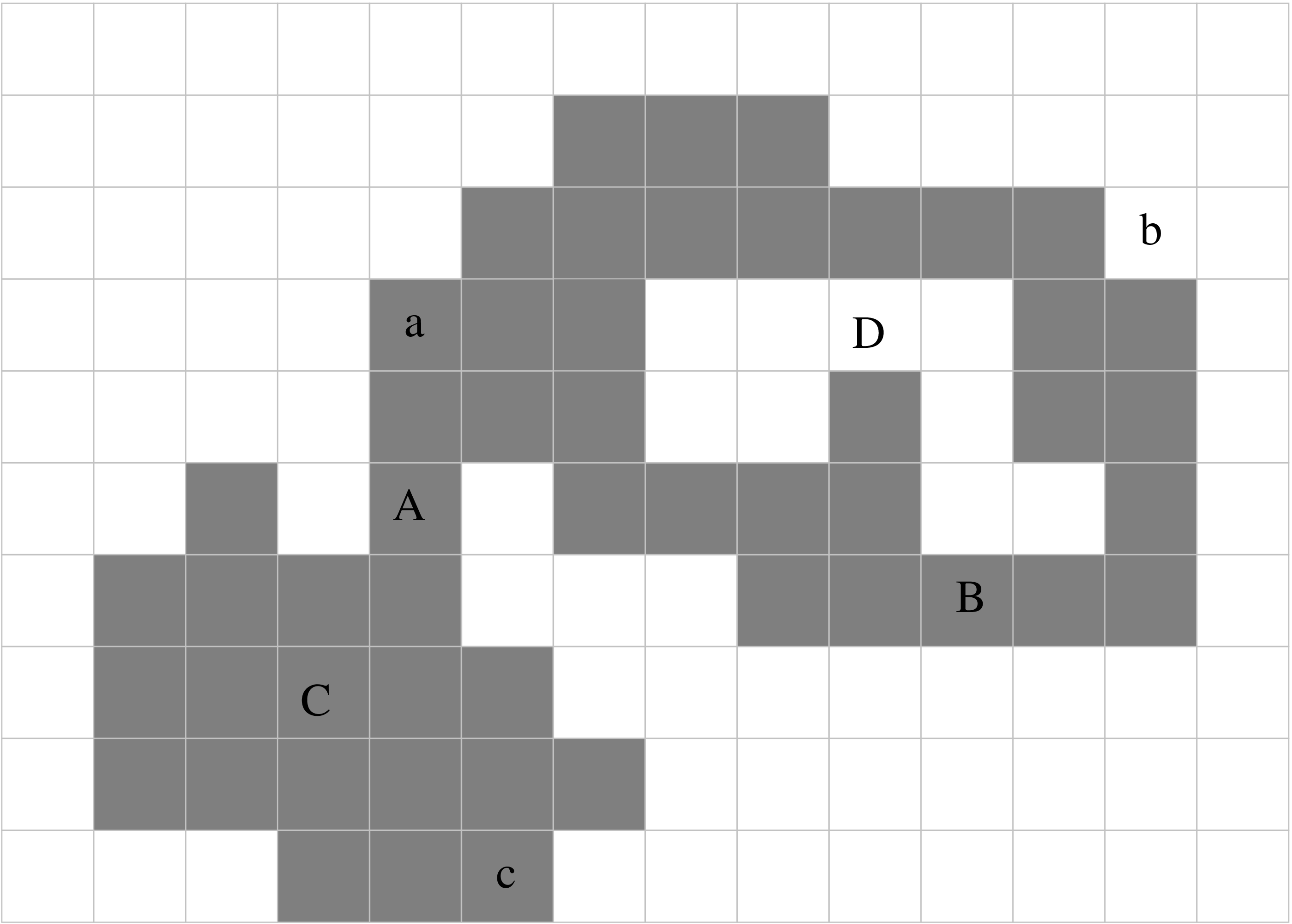
(which are resp. (0,1)- and (1,0)-simple ?)
Main Results
Thm.
In dimension 2 and 3,  -simplicity of
-simplicity of  can be decided locally at
can be decided locally at 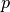
(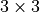 neighborhood in 2D,
neighborhood in 2D, 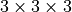 )
)
E.g. 2D
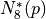 : 8-neighborhood around
: 8-neighborhood around 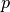 (without p)
(without p)
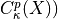 : set of
: set of  -connected components in
-connected components in 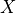 adjacent to
adjacent to 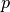
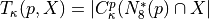
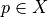 is
is
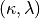 -simple for
-simple for
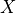
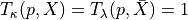
In dimension 3,  definition is a bit more complex but still local
definition is a bit more complex but still local
All configurations in 2D

|

|
| (0,1) | (1,0) |
Idea
Iterate until stability over sequential simple points removal  ultimate homotopic thinning
ultimate homotopic thinning
|
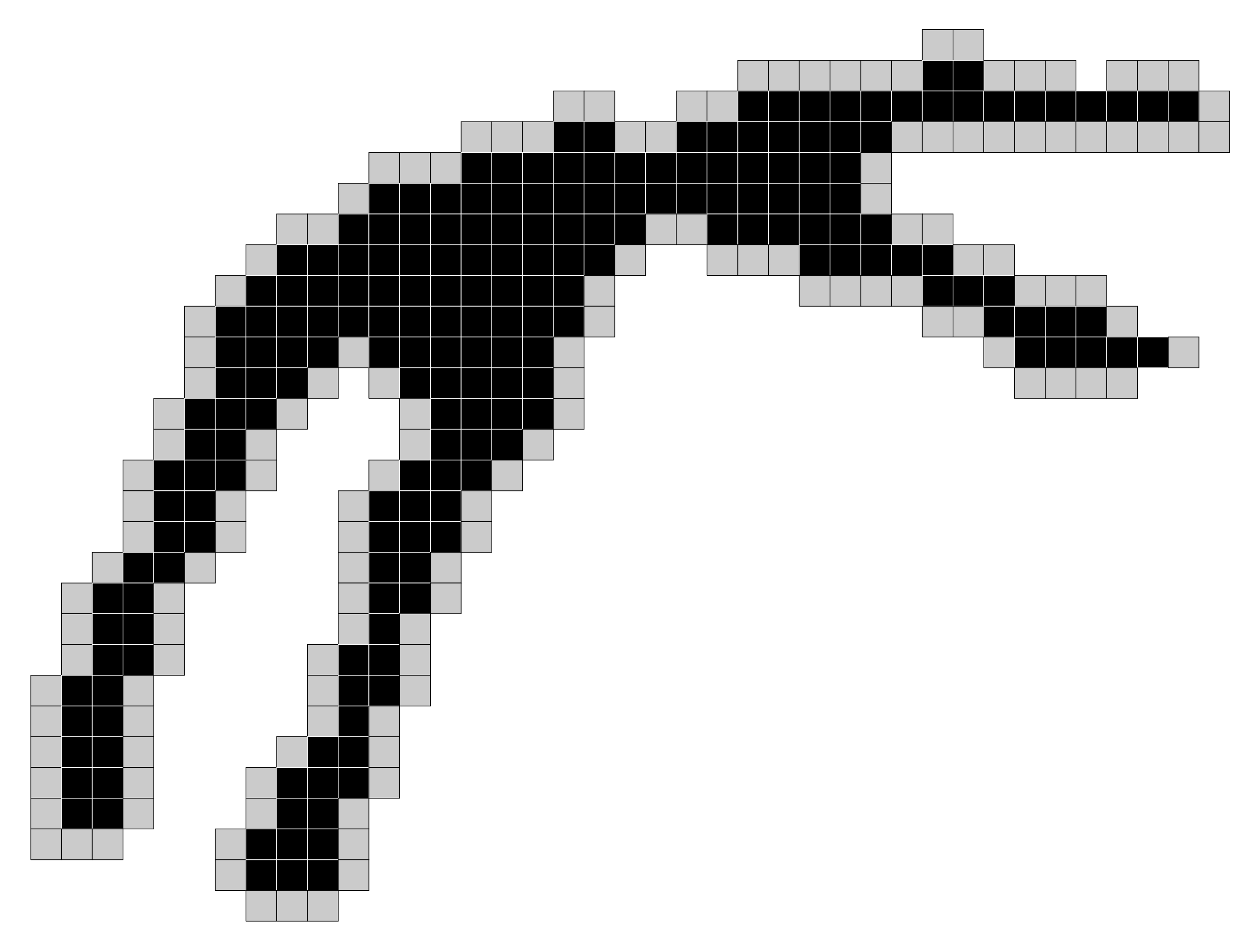
|
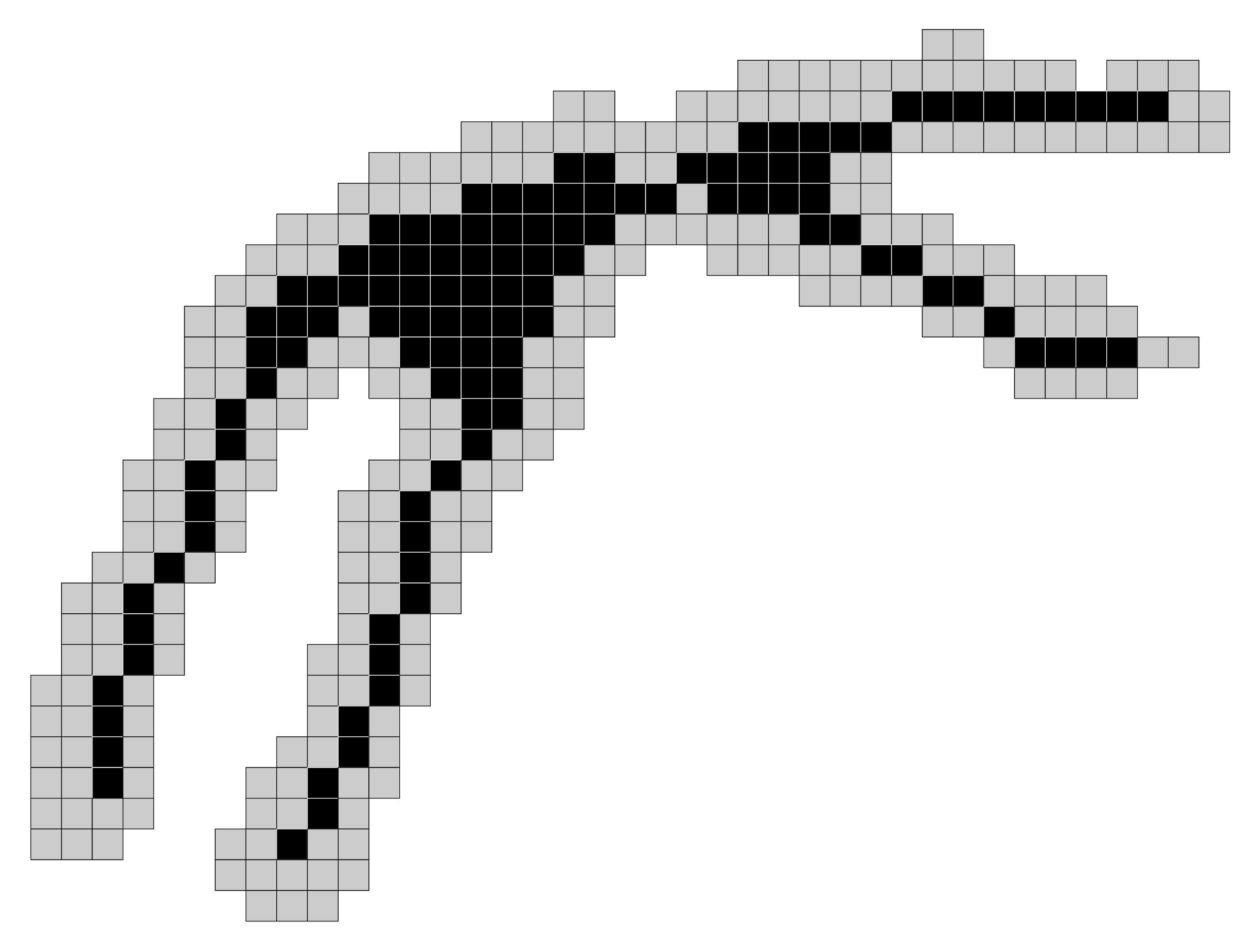
|
|
P = { p in X | p is simple for X }
while ( P != empty )
Q = emptyset
for all points p in P
if (p is simple for X)
X = X \ {p}
for all q in N(p)
Q = Q + {q}
P = emptyset
for all points p in Q
if (p is simple for X)
P = P+ {p}
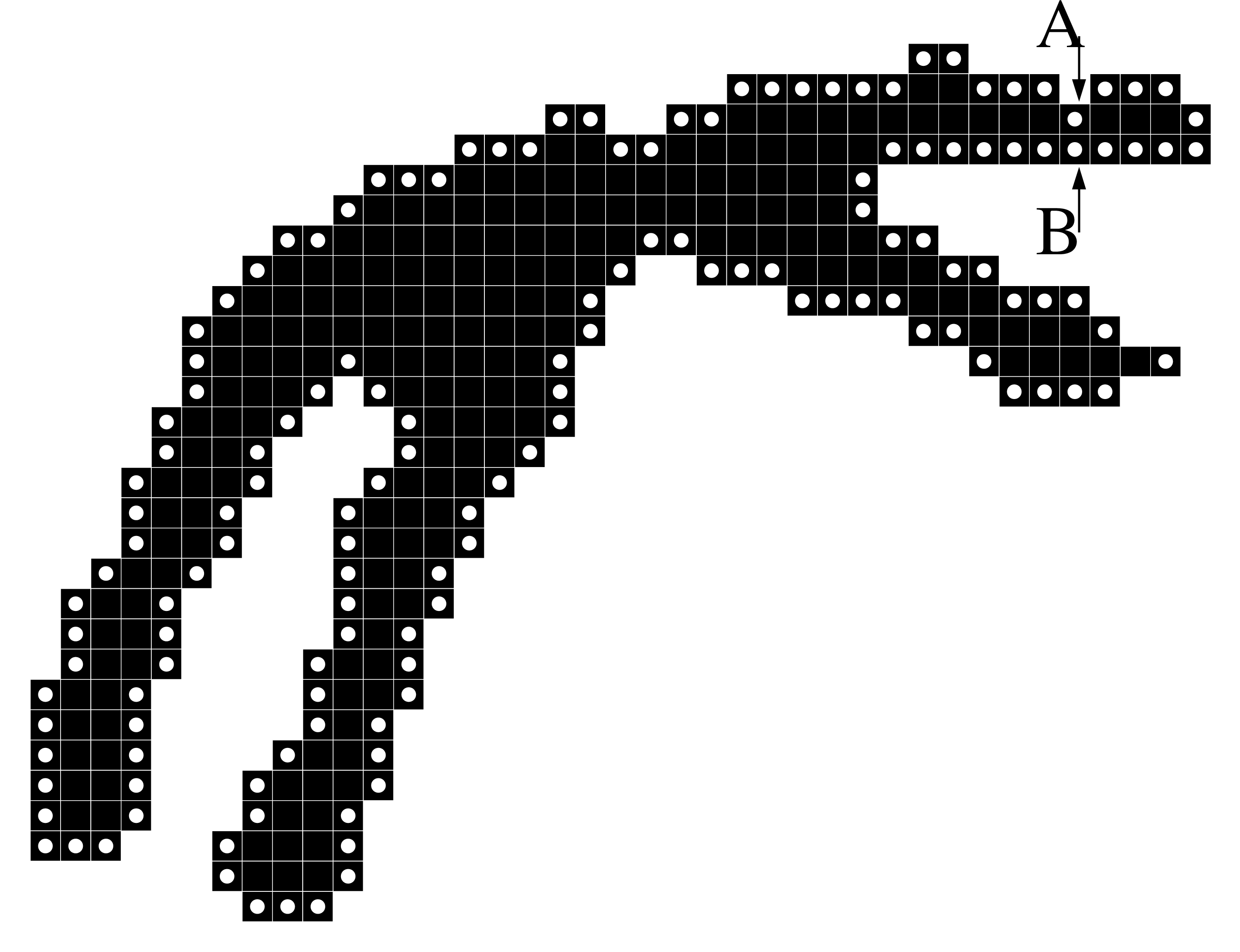
Idea
Based on an Oracle, we decide to block some simple points during the thinning
Generic algorithm
Breadth first thinning if P is implemented as a queue
P = { p in X | p is simple for X }
while ( P != empty )
Q = emptyset
for all points p in P
if (p is simple for X) and (p is not anchor point)
X = X \ {p}
for all q in N(p)
Q = Q + {q}
P = emptyset
for all points p in Q
if (p is simple for X)
P = P+ {p}
E.g.
p is anchor point if it has only one neighbor in X
|

|
Idea
Anchor points can be specified to generate surface based skeleton

|

|
Guided Thinning
Instead of using a queue for P, we consider a priority list with distance transformation values
 Better geometry (central axis) of the skeleton
Better geometry (central axis) of the skeleton
Parallel thinning
 usually, parallel thinning algorithms are more efficient and provide centered skeletons
usually, parallel thinning algorithms are more efficient and provide centered skeletons
Active works