Introduction, numerical images and geometrical representation
Preliminaries
Goals
Lectures
- Introduce fundamental concepts in computer graphics, image
processing, digital geometry and computational geometry
- Illustrate links between geometrical analysis of shapes and related
fields (complexity, arithmetic, word theory, ….)
Practical work (TP)
- Implement some image processing/shape analysis tools
- Comparative evaluation principles (tests, asymptotic
vs. experimental computational costs…)
Infrastructure
Github project https://github.com/dcoeurjo/lectureDG
- Lecture sources
- Practical work
git clone https://github.com/dcoeurjo/lectureDG.git
Practical work
Homework, project, final exam
- One practical work session will be evaluated
- Homework
- Final exam
Context: Analysis of geometrical objects
Geometrical objets
- From acquisition devices
- CCD devices
- tomographic images (IRM, scanners X, …)
- From modeling processes
- Geometrical modelers, CAD (computer-aided design)
- From mathematical modeling of phenomena
Analysis
- … computer-based -> algorithms
- … quantitative
- Scalar shape descriptors
- Geometrical paramters
- Topological invariants, …
- -> quality, robustness, certified computations, …
Couple of Acquisition Devices
CCD Device
Charged-Coupled Device
Principles photo-active regions/pixels : each unit if surface
element accumulate some electrical charges proportional to the
intensity of received light
photon -> electron charges

|

|
|
| Linear device |
2D device |
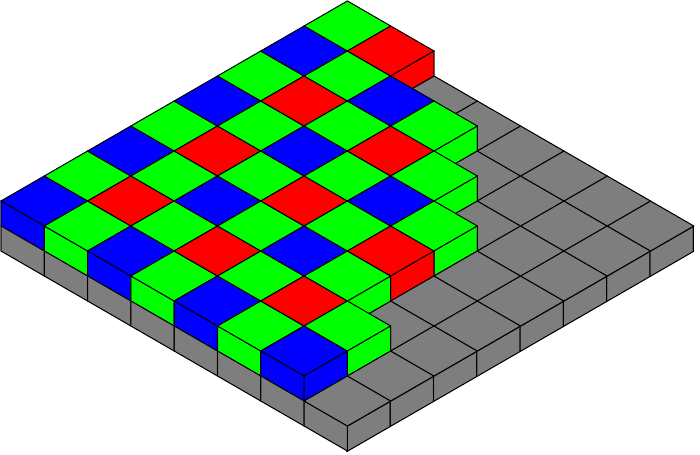
Bayer pattern |
Physical notion of pixels
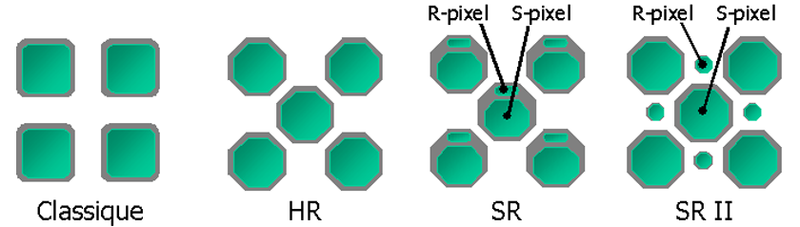
Associated Modeling
By construction
- Underlying support geometry is induced by a periodic tiling
- Values are quantified on a small number of bits
def.
Image: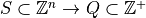
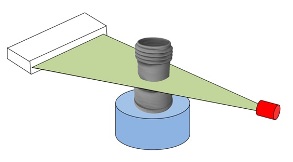
Tomography
Principles
- particles are emitted (ions, protons, photons, …) from a source
device to a target (object, body, …)
- a detector measures particles intensity after the object
traversal. The intensity decay is a function of the time flight and
the traversed material)
- the image is reconstructed from attenuation measurements using
back-projection approaches
Tomography (bis)
Basic Idea Radon’s Theorem
 = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x,y)\delta(t-x \cos(\theta) - y \sin(\theta)) dxdy](_images/math/96aa0df6f43c74973176e754d34495523cb2d3ca.png)
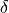 Dirac measures
Dirac measures
<demo>
Digital Tomography
Specificities
- Projection directions: rational straight lines
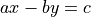 (
(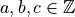 )
)
- Projection function: sum of digital point values along the rational
straight line
- Data to reconstruct: binary values {0,1} or in
Problems
- Number of required projections
- Uniqueness of the reconstruction
- Sometimes, further hypotheses are required (convexity,
smoothness, …)
|
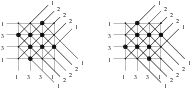
|
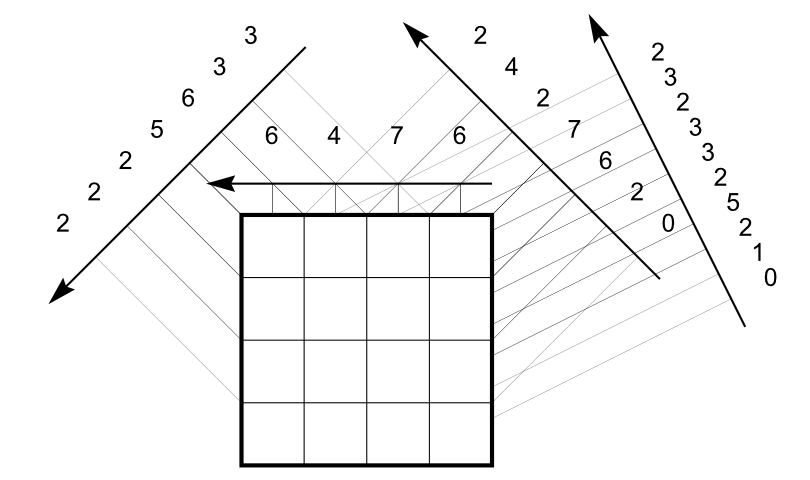
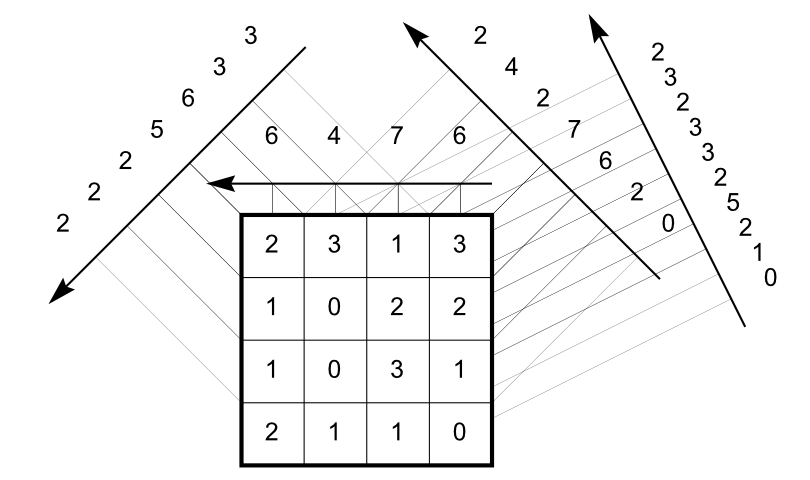
Example: Mojette Transform
Digital Tomography: conclusion
By construction or for efficiency of the reconstruction process
from projections, the result isusually defined in regular lattices
in 2D or 3D
def.
Image: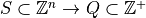
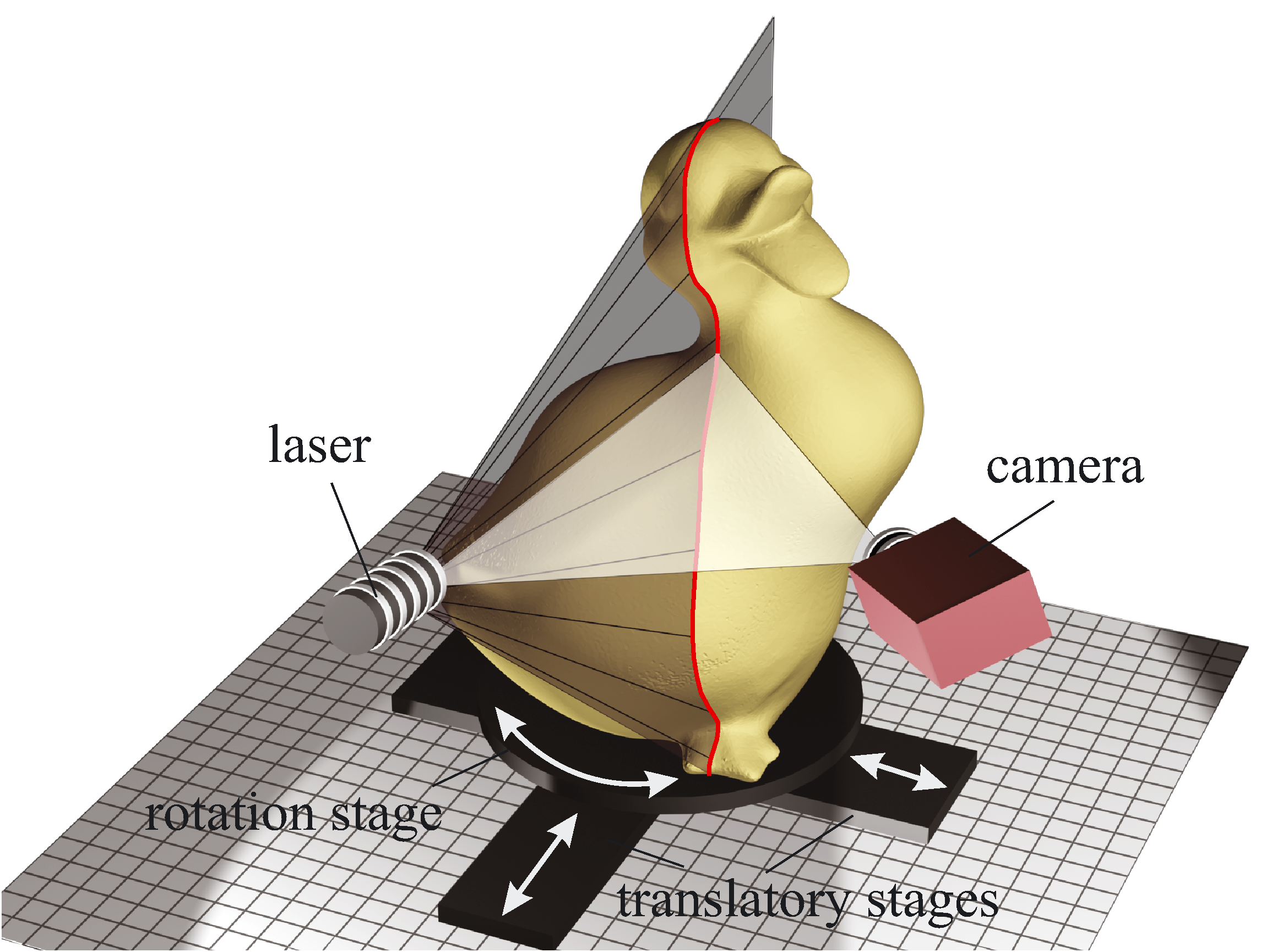
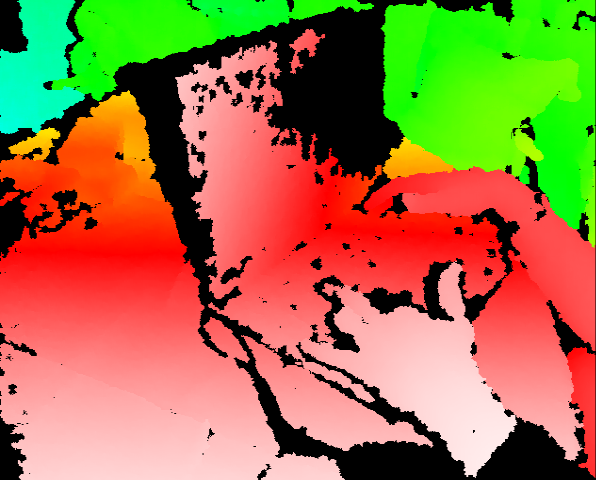
Acquisition from laser/ultrasound/contact
Mechanical contacts probe measurements from motorized systems
Approches based on time-of-flight computations (e.g. laser or
sonar rangefinder, …)
- measures the time taken by the pulse to be reflected off
the target and returned to the sender
- data = distance of the target from the source en a set of
directions. After reconstruction,
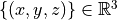
|

|
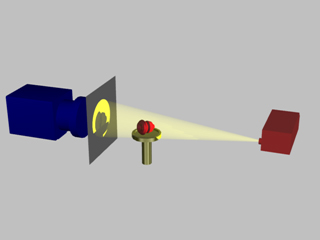
Reconstruction from triangulation principle
- Input: a pulse (or series of) is emitted from the source
- and observed if a detector (ex. laser + CCD)
- Relative position of the source and the detector is known
and thus
- From 2D positions in the detector,
- data = After calibration and reconstruction, a point cloud
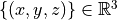
|
|
Reconstruction from images: example with Epipolar Geometry
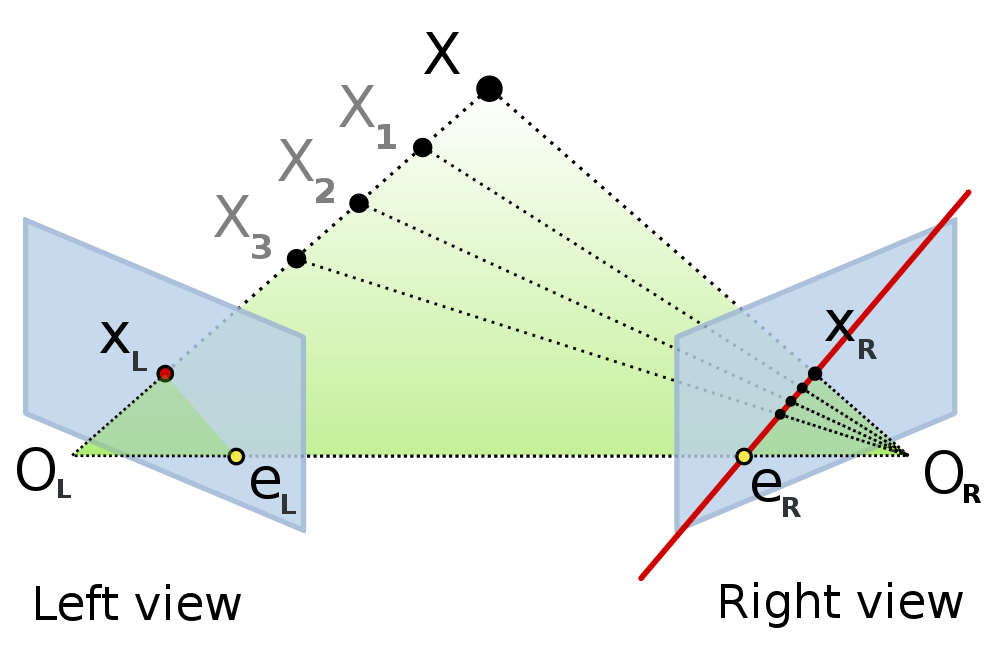
Hybrid approach: Kinect
- Color camera (CCD, 640x480)
- Pattern projection in infrared + CMOS detector (~640x480)
|

|
Raw data = Depth map in the detector plane + color image
Quiz: why infrared ?
Bottlenecks/Problems to consider
- Filtering (noise, outliers,…)
- Point cloud registration (by device calibration or from data processing)
- Local density control
- How to deal wit occluded regions ?
- …
Bottlenecks/Problems to consider (bis)
Geometrical reconstruction define a high quality manifold
approximating or interpolating the point cloud.
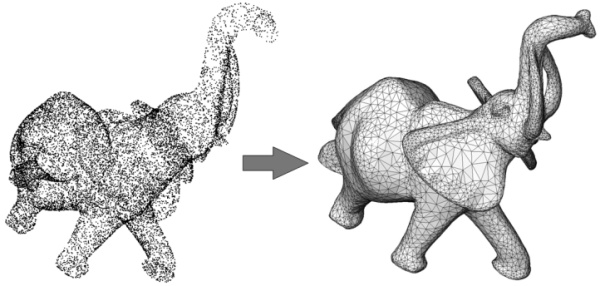
- Manifold cf later
- Quality
- distance to samples (which metric ? how to be robust to noise ?…)
- Smoothness of the reconstruction
- Geometrical and topological certificate of the reconstruction
- …
Some External Devices
Raster Screens
Principles
- Luminophores with RGB cells (red, green, blue) to render colors
by additivity
- In our context
- Color image :
![[0..n]\times[0..m] -> Q^3](_images/math/1b1d7e44495ba22e25035d39cd16e05a7a06487b.png)
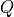 : range of each color channel (8bits, 24bits, …)
: range of each color channel (8bits, 24bits, …)
Problems
- Rendering problem: geometrical models
 digital representations
digital representations
- ex: straight lines/circles drawing…
3D printers
Layer based
- Additive approach: material is added layer by layer
- Several technologies: heated plastic layers, stereolithography
(solidification of the polymer resin from ultra-violet beam), …
- Key point : slice based or discrete representation
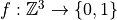 of the object to print
of the object to print
Problems
- Geometrical model
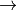 layer based representaiton
layer based representaiton
- How to control the topology/surface orientation during the process ?
- Some geometrical analysis can be performed to enforce stability,
robustness, …
Topics Overview
(Very) Short (Subjective) Glossary
Image Processing (traitement et analyse d’images)
- General image related topic
- Image as the “realization” of a bi-directional signal
- keywords: image compression, filtering, denoising, color analysis, shape segmentation,…
Computer Vision (Vision par ordinateur, reconnaissance de formes,..)
- Focusing on object perception
- Keywords: Shape recognition, shape/image indexing and retrieval, 3D
reconstruction from images, …
(Very) Short (Subjective) Glossary
Computational Geometry
- Discrete data (point sets, simplicial complexes, …)
- Aim to first reconstruct structures and perform
geometrical/topological computations
- Certified computations
- Complexity
Digital Geometry
- We focus on discrete data defined on lattices (
 integer coordinates, arithmetical properties of objects…)
integer coordinates, arithmetical properties of objects…)
- Values are usually binary
- take geometrical/topological decisions from objects defined by
extension (vs. from properties)
(Very) Short (Subjective) Glossary
Geometric Modeling
- Model objects and complex geometrical scenes
- Procedural modeling, animation, …
Image Synthesis
- Image rendering from geometrical models + material properties +
Illumination models
- Ray shooting, radiosity, photon path tracing, ….
Overview of the course
TOC
Image Processing
- Image filtering
- Colorimetric (historgram) processing
- Mathematical morphology
- Segmentation
Digital Geometry
- Digital model and Digital topology
- Digital object surface analysis
- Volumetric processing
- Fast arithmetical transforms
Computational Geometry
- Geometrical predicates, convex hulls, Delaunay triangulations
- Spatial Data structures
- …







 = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x,y)\delta(t-x \cos(\theta) - y \sin(\theta)) dxdy](_images/math/96aa0df6f43c74973176e754d34495523cb2d3ca.png)
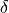 Dirac measures
Dirac measures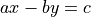 (
( )
)

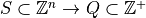







![[0..n]\times[0..m] -> Q^3](_images/math/1b1d7e44495ba22e25035d39cd16e05a7a06487b.png)
 : range of each color channel (8bits, 24bits, …)
: range of each color channel (8bits, 24bits, …)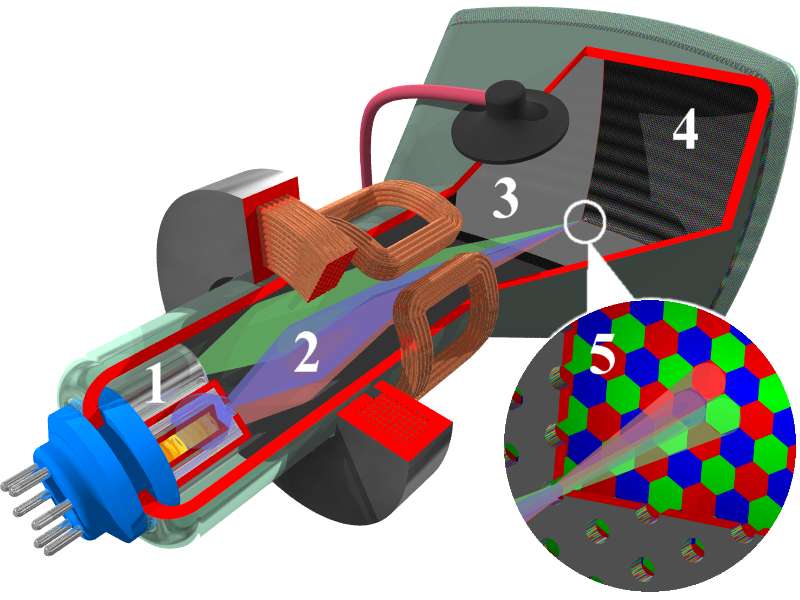


 digital representations
digital representations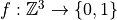 of the object to print
of the object to print

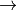 layer based representaiton
layer based representaiton integer coordinates, arithmetical properties of objects…)
integer coordinates, arithmetical properties of objects…)