Mesh Processing§
| author: | David Coeurjolly |
|---|
| author: | David Coeurjolly |
|---|
Rough definition
Def.
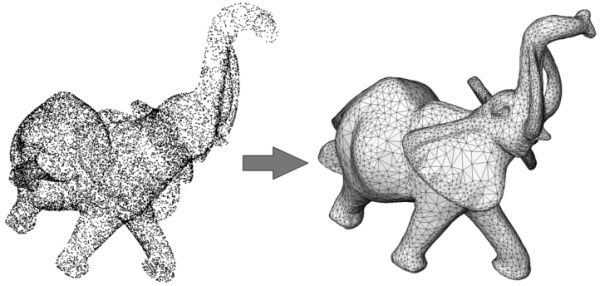
A mesh is a piecewise linear geometrical structure embedded in 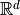
Usually, we assume
For instance, we can consider
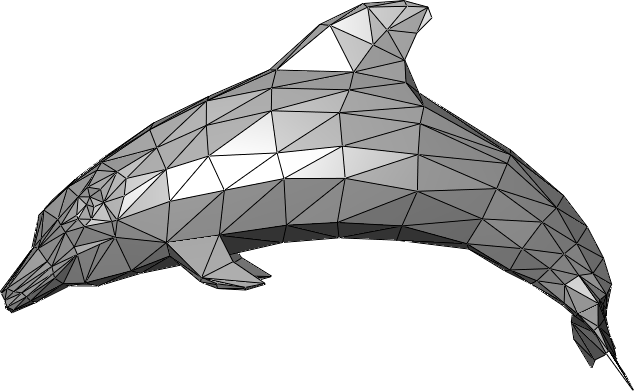
|
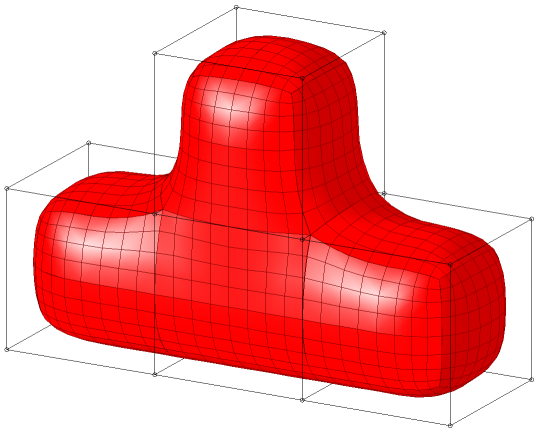
|
|
| Triangular meshes | Quadtrilateral meshes | Tetrahedral meshes |
Why meshes?
Cellular structure
Vertices (0-cell), edges (1-cell), triangles (2-cell), tetrahedon (3-cell)  simplices
simplices
Def. Simplex
A k-simplex is a k-dimensional polytope which is the convex hull of its k + 1 affinely independent vertices
Def. Simplicial Complex
A simplicial complex  is a set of simplices that
satisfies the following conditions:
is a set of simplices that
satisfies the following conditions:
 is also in
is also in 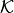
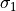 ,
, 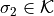 is a face of both
is a face of both 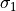 and
and 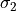
|
|
 Strong topological structure (order, boundary, co-boundary,
each simplex is topological ball)
Strong topological structure (order, boundary, co-boundary,
each simplex is topological ball)
 Many topological operations on meshes can be described as k-simplices operations
Many topological operations on meshes can be described as k-simplices operations
 Specific combinatoric makes implementation easy
Specific combinatoric makes implementation easy
We remove the constraint that k-cells are defined by k+1-vertices

..but..
 restricted cases (CW-complexes)
restricted cases (CW-complexes) combinatorial characterization (Combinatorial Maps)
combinatorial characterization (Combinatorial Maps)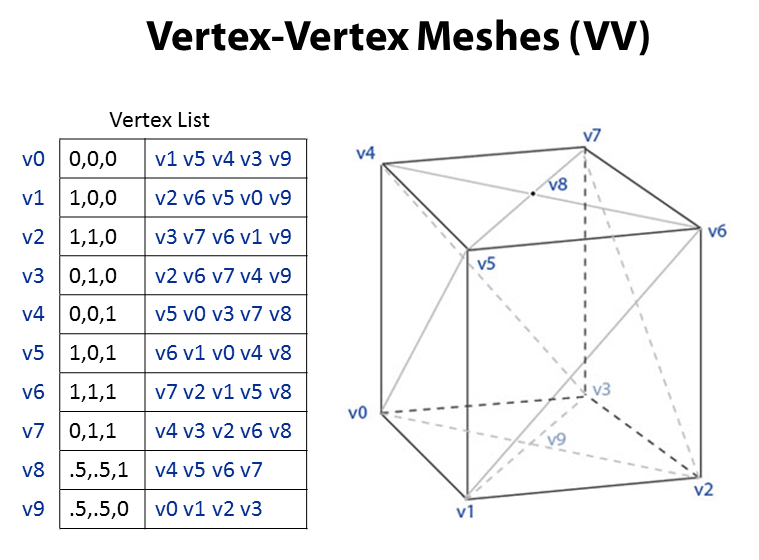
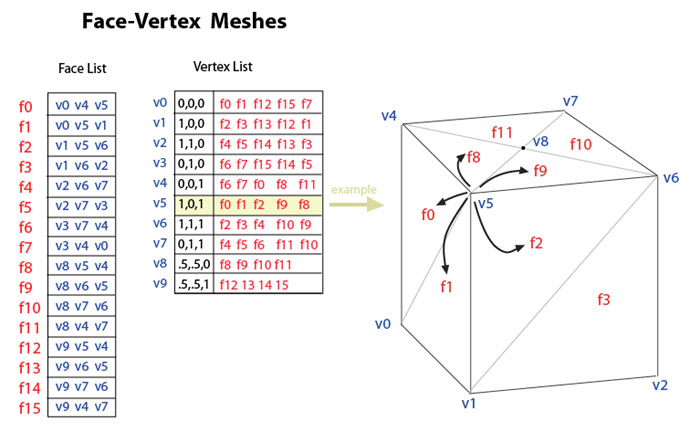

Neighboring faces for triangular meshes can be stored in a explicit structure
AdjF:
…but… not efficient for cellular meshes
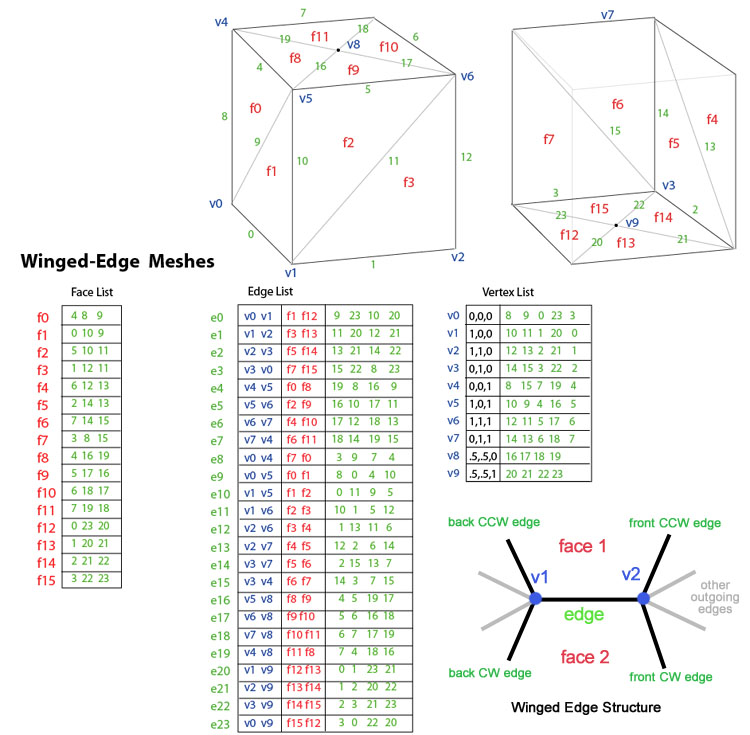
Double-linked list of edges
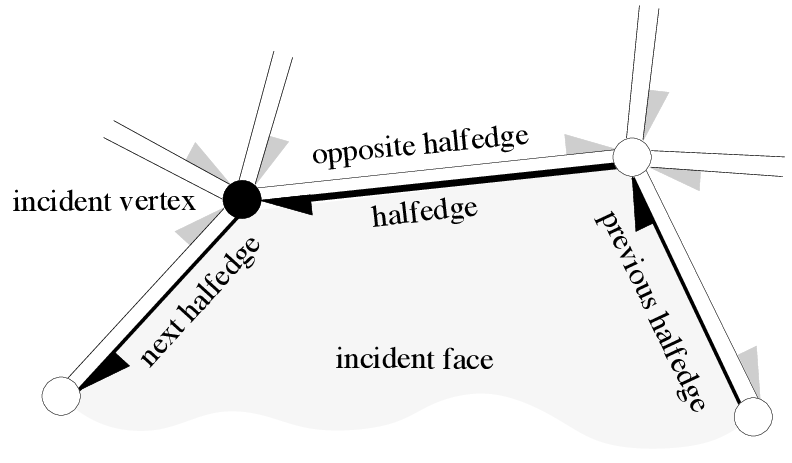
cgal.org
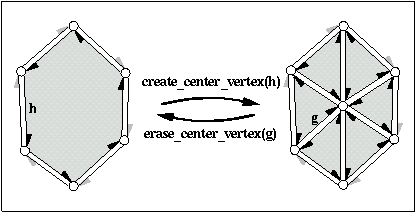
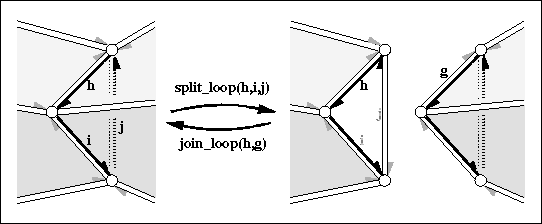
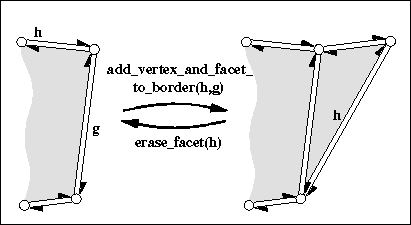
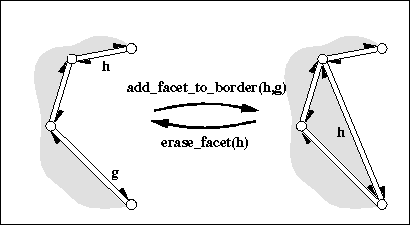
Core topological operations maintaining the structure
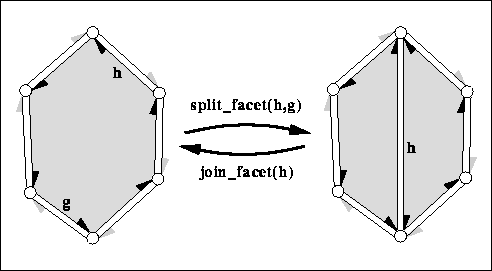
|
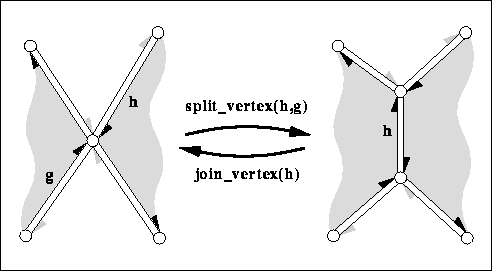
|
|
|
|
|
cgal.org
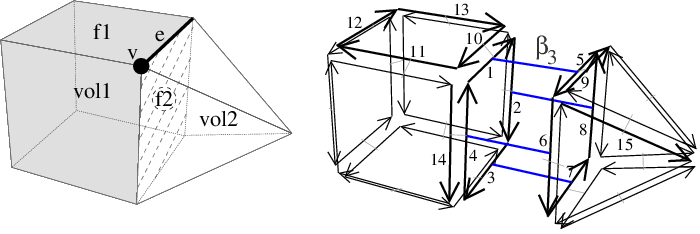
Valid combinatorial model in any dimension
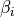 (
( )
on dart labels to encode the structure
)
on dart labels to encode the structure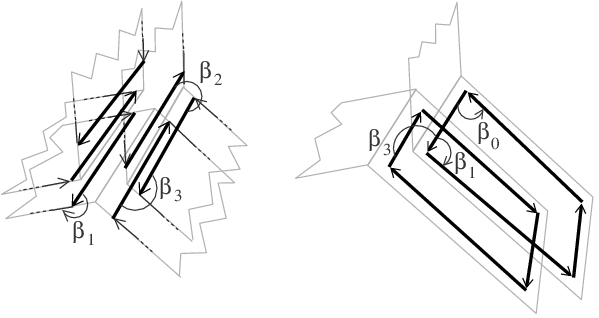
|
|
cgal.org
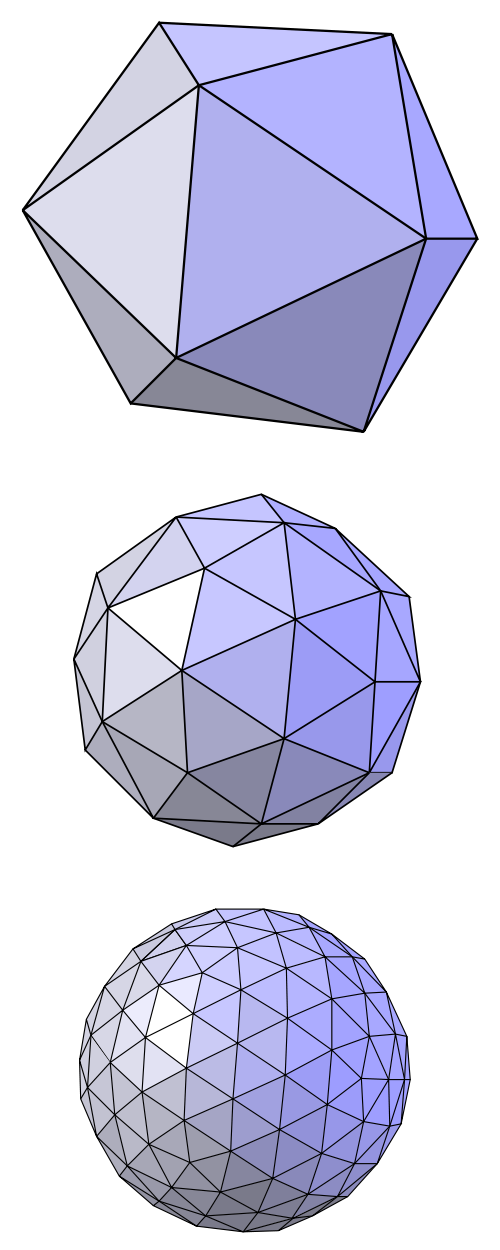
Principle
Start from a control mesh and apply local subdivision rules to generate finer object.
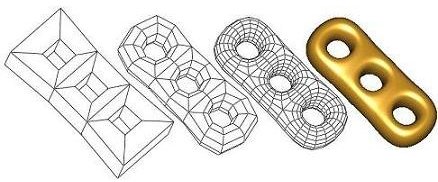
Subdivision rule
Main idea: from the subdivison mechanism we can prove that the
limit surface is (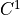 ,
, 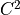 ,…)
,…)
Related to B-spline schemes
|
|
|
(resp. Catmull-Clark, Loop, Doo-Sabin)
Principle
Optimize the size of input mesh removing unnecessary triangles
More formally
Compute 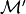 with
with
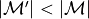 and
and
What kind of shape metric d ?
Local metric evaluation
 , we remove the point
and triangulate its one-ring
, we remove the point
and triangulate its one-ring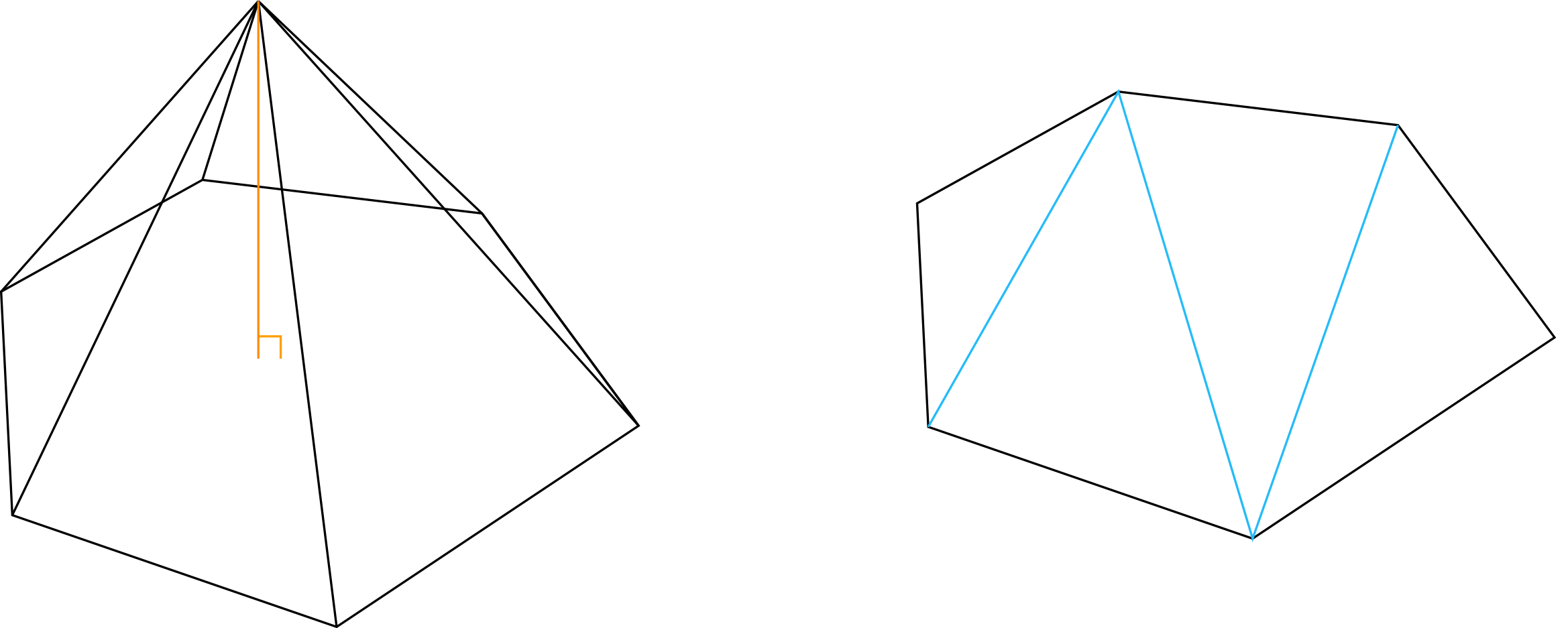
|
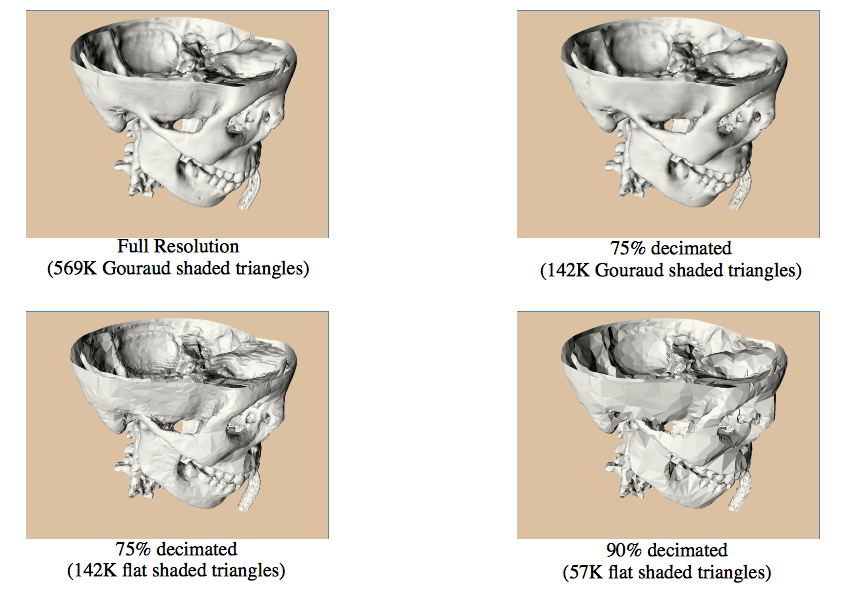
|
Fast and easy implement but
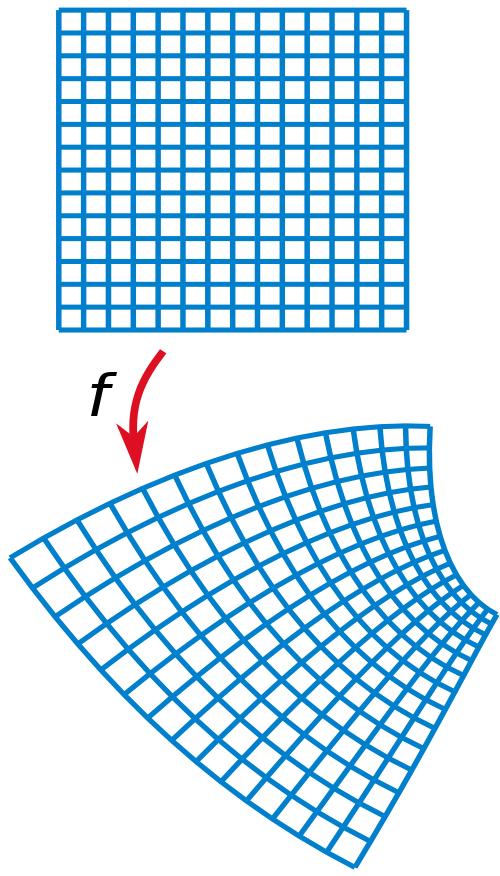
Idea
Parametrized a complex mesh (2-manifold) on a 2D parameter space ![[U,V]](_images/math/05a73472bed6968261ac2fbf78437212400f53f2.png)
Issues
Many applications
|

|
Conformal Parametrization
|
|
Discrete formulation
Defs.
Two meshes 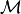
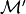 with same
topology are (conformally) equivalent iff
with same
topology are (conformally) equivalent iff 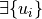 such that
such that
or equivalently (logspace)
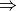 linear formulation
linear formulation
Topological issues

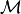 is homeomorphic to a disk, there exist a
conformal map to plane [U,V]
is homeomorphic to a disk, there exist a
conformal map to plane [U,V]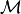 is homeomorphic to a sphere, there exist a conformal map from
is homeomorphic to a sphere, there exist a conformal map from 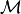 to a unit sphere
to a unit spherePractical solution: Cut and Open
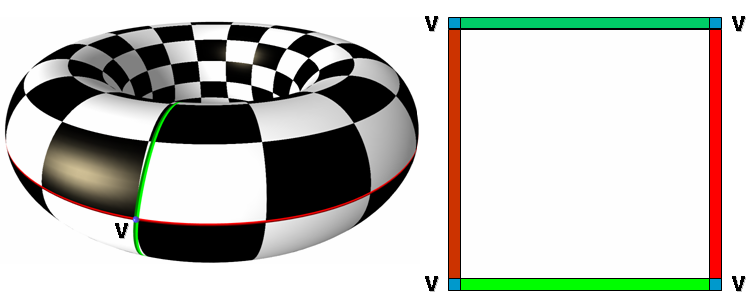
Idea
Half-edge or Vertex-Edge data structure contains redundant information that can be compressed
We want to
Example: Triangular strip
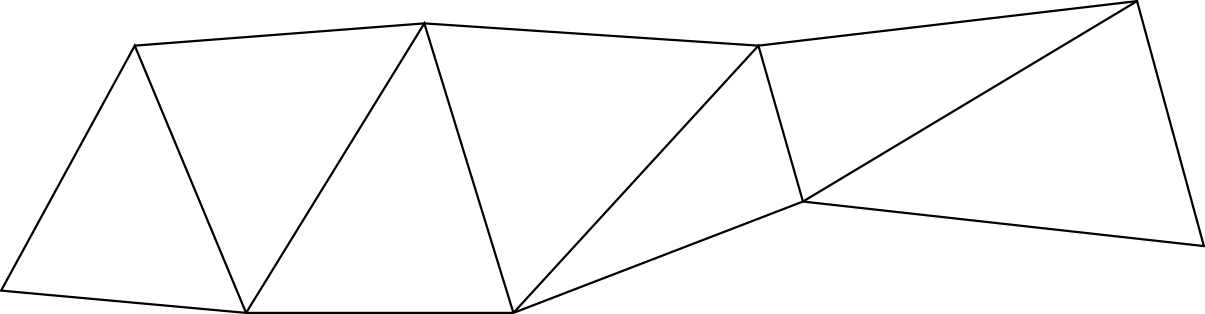
<see blackboard>