Digital Geometry: Digital Model and Elementary Digital Topology§
| author: | David Coeurjolly |
|---|
| author: | David Coeurjolly |
|---|
Idea
Take benefit from the regular structure of the lattice to enhance geometrical analysis of shapes
|

|
|
Requirements
More formally
Lattice
Given a basis  of
of 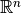 ,
,
(finitely-generated free abelian group, symmetry group, …)
Five fundamental lattices in the Euclidean plane
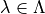 is its Voronoi cell
is its Voronoi cellFollowing fundamental lattice classification: pavings by squares, hexagons, triangles, rhombi and parallelograms.
By definition, the paving induced by a lattice is periodic
Triangular/Hexagonal lattice/paving are dual
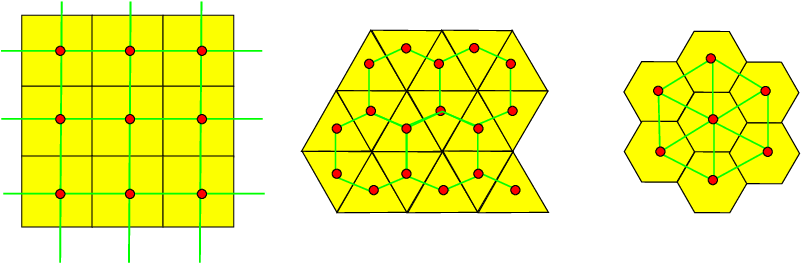
Speaking of density packing/kissing number and covering, hexagonal lattice is optimal
Regular cubic grid
Face-centered cubic grid
Body-centered cubic grid
BCC has optimal covering
FCC has highest packing density and largest kissing number
FCC and BCC are dual
Hexagonal grid
Definition
Square lattice
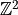 , direct access to direct neighbors
, direct access to direct neighbors 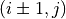 ,
, 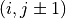
Triangular grid
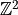 , three direct neighbors (two local configurations when mapped to
, three direct neighbors (two local configurations when mapped to 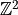 )
)Hexagonal grid
Cubic grid
Trivial
FCC/BCC grid
Elongated grids
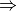 Remapping
Remapping 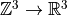 on-the-fly
on-the-flyCombinatorial approach
In 2D:
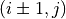 and
and 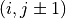
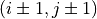
In 3D:
Topological approach
Two pixels/voxels are (k)-adjacent is the intersection of their (closed) cell is of dimension 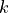
Mixing all dimensions:
 (1)-adjacent
(1)-adjacent (0)-adjacent
(0)-adjacent (2)-adjacent
(2)-adjacent(k)-path
A sequence of digital points 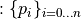 is a (k)-path if for each point,
is a (k)-path if for each point, 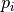 is (k)-adjacent to
is (k)-adjacent to 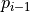 (except for
(except for 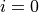 )
)
(k)-arc
A (k)-arc is a (k)-path such that each 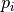 has exactly two (k)-adjacent neighbors (except for extremities)
has exactly two (k)-adjacent neighbors (except for extremities)
(k)-curve
A (k)-curve is a (k)-arc such that 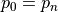
(k)-object
A set S of digital point is a (k)-object iff for any pair of points, there exists a (k)-path in S
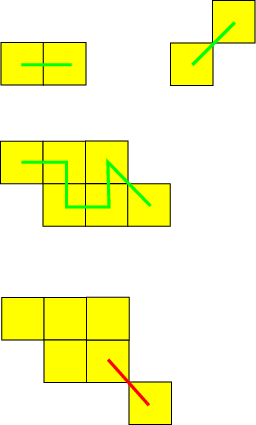
|
|
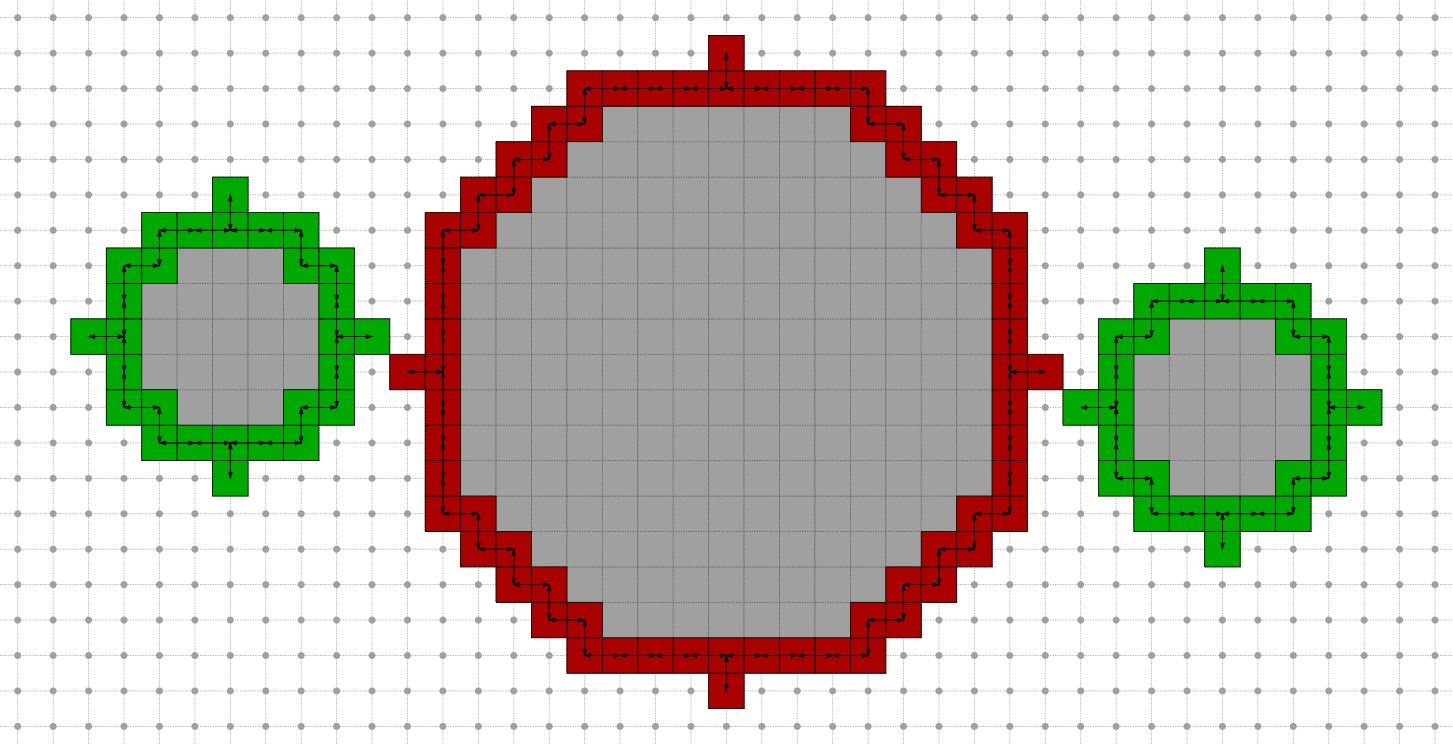
Can you spot (k)-arcs/(k)-objects/(k)-curves for 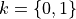 ?
?
Objective: define a notion of object contour/boundary matching with Jordan theory
 is a Jordan curve (or simple closed curve) in
is a Jordan curve (or simple closed curve) in  if
if 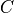 is the image of a continuous and injective map from the circle to
is the image of a continuous and injective map from the circle to 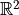
Jordan theorem states that:
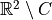 has two connected components, one is bounded (aka interior) and the other one is unbounded (exterior)
has two connected components, one is bounded (aka interior) and the other one is unbounded (exterior)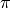 from an interior point to an exterior one crosses
from an interior point to an exterior one crosses  (with an odd number of intersections)
(with an odd number of intersections)
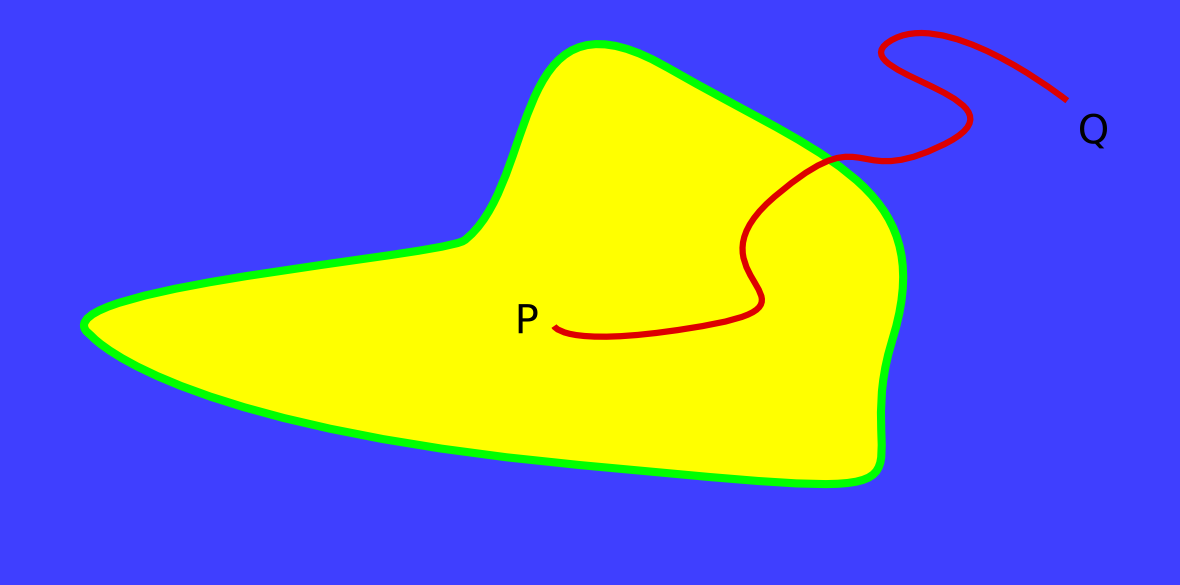
Idea mimic a digital version of Jordan framework replacing  by a (k)-curve ?
by a (k)-curve ?
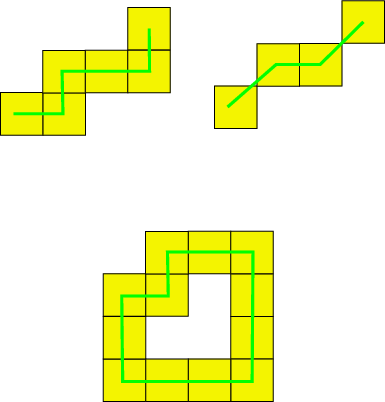
Given the following (0)- and (1)-curves, do they define Jordan-like curve ?
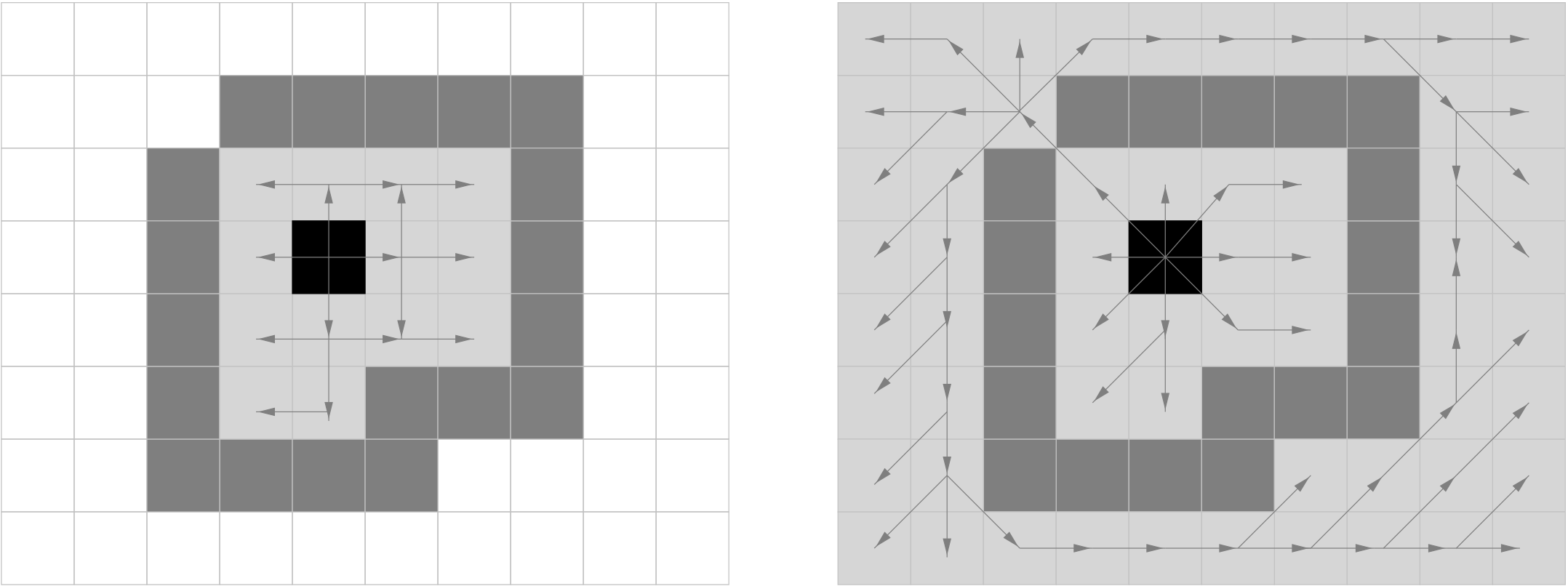
 Jordan pair such that k is the adjacency for the object and l the adjacency for the complementary
Jordan pair such that k is the adjacency for the object and l the adjacency for the complementary
In dimension 2
(0,1) and (1,0)
In dimension 3
(2,1), (2,0) (1,2) and (0,2)
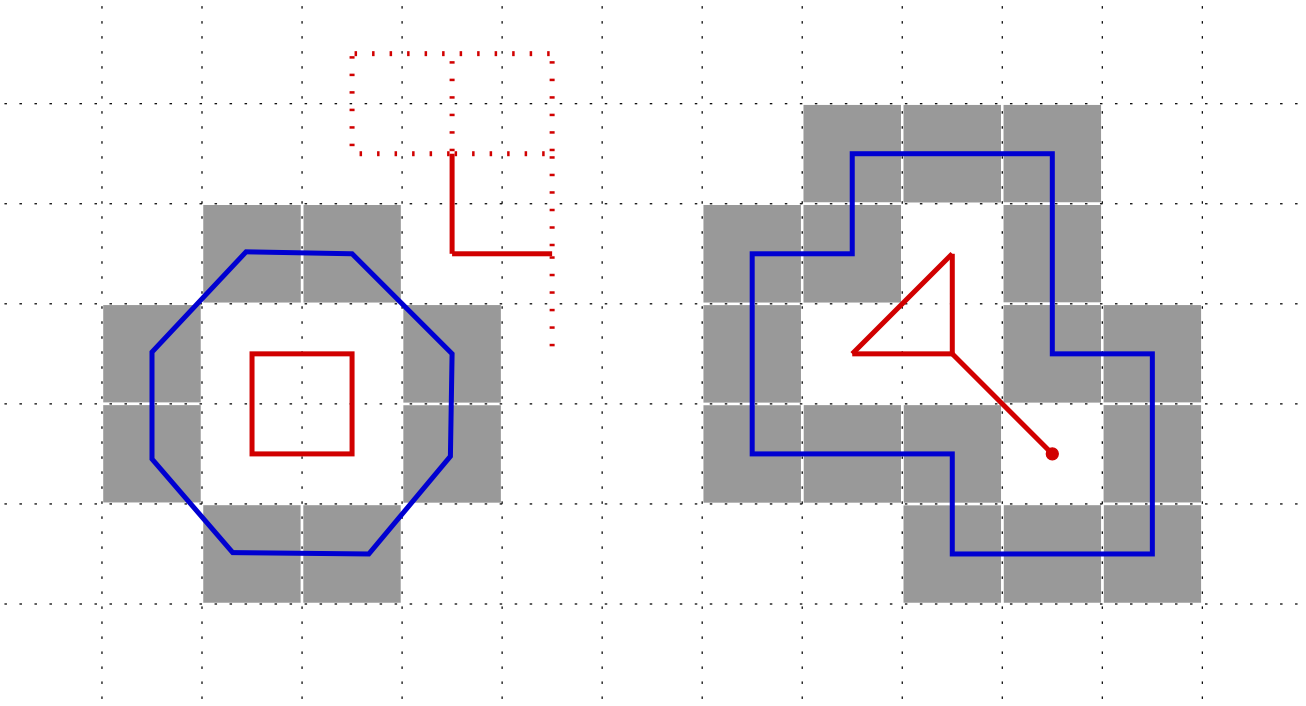
Border: Given a  Jordan pair, the border of
Jordan pair, the border of 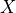 is the set of
is the set of 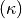 -adjacent digital points which are
-adjacent digital points which are 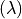 -adjacent to points in
-adjacent to points in 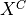
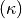 -object but we need more constraints to have a
-object but we need more constraints to have a 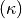 -curve
-curve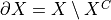 (or kind of, both are considered as open sets)
(or kind of, both are considered as open sets)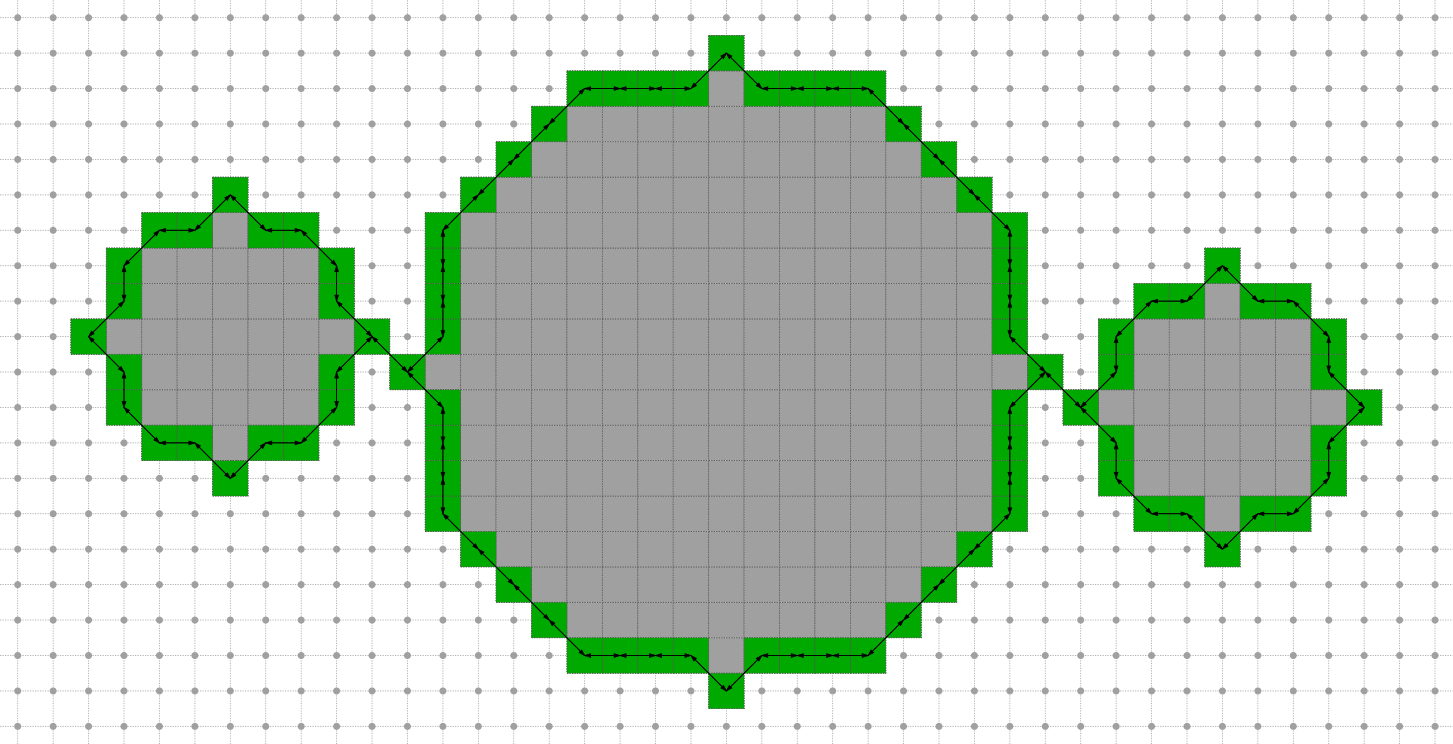
|
|
Idea embed the digital space 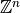 into a cellular space (cartesian cubic space) to represent oriented inter-pixel elements
into a cellular space (cartesian cubic space) to represent oriented inter-pixel elements
In 2D
 are embedded into 0-cells
are embedded into 0-cellsIn nD
(two 0-cells, two 2-cells and four 1-cells)
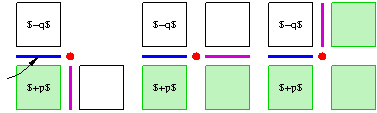
Principle defines digital surface as a set of (n-1)-cells (surfels)
 relationship on surfels (anti-reflexive, local transitive closure, locally defined)
relationship on surfels (anti-reflexive, local transitive closure, locally defined) Jordan adjacency pair,
Jordan adjacency pair,  triplet is a Jordan triplet
triplet is a Jordan triplet
is anti-reflexive
is a relationship on surfels
can extract all surfels (informally)
We can demonstrate that such Jordan triplets leads to well-defined digital Jordan surface
Illustration in 2D (here, k=1)
Approach is valid for various digital structures
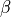 in 3D§
in 3D§Two valid 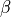 relationships on (2,1)- or (2,0)- pairs on closed objects
relationships on (2,1)- or (2,0)- pairs on closed objects
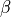 relationship + graph traversal (depth first, breadth first,…)
relationship + graph traversal (depth first, breadth first,…) 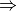 digital surface tracker
digital surface tracker
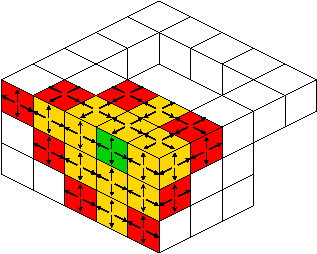
|
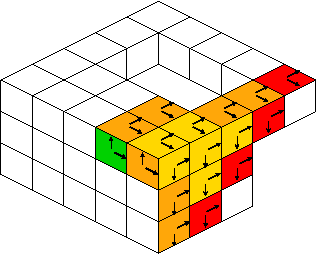
|
Efficiency of the tracker is guided by the `beta`:math: complexity
For (2)-object
 is not oriented, each surfel is processed 4 times
is not oriented, each surfel is processed 4 times with oriented arcs (2 arcs per surfel), each surfel is processed 2 times
with oriented arcs (2 arcs per surfel), each surfel is processed 2 times with oriented arcs (1 or 2 arcs per surfels), each surfel is processed 4/3 times (on average)
with oriented arcs (1 or 2 arcs per surfels), each surfel is processed 4/3 times (on average) Hamiltonian path exists if
Hamiltonian path exists if  is homeomorphic to a ball
is homeomorphic to a ballOverall algorithm (for single connected surface)
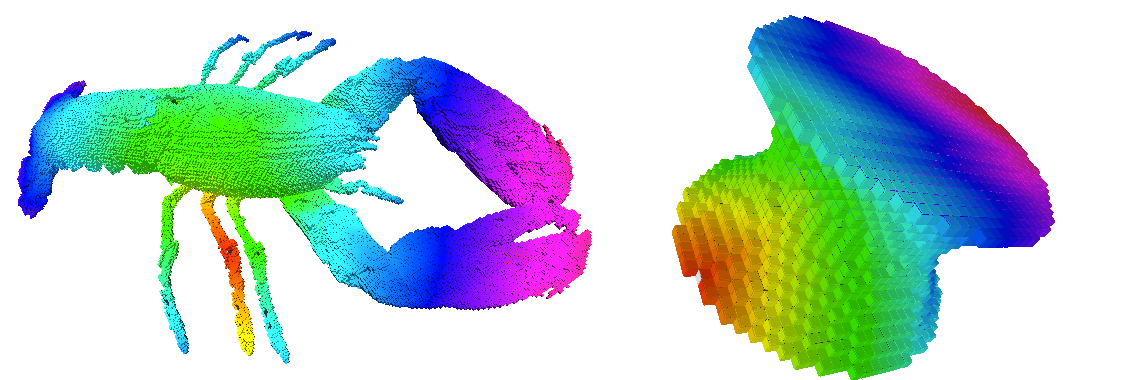
Complex Objects
Several connected components, holes, …
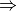 Scan the complete volume, mark all surfels as potential starting surfels and apply the tracker on each starting surfel (removing traversed surfels)
Scan the complete volume, mark all surfels as potential starting surfels and apply the tracker on each starting surfel (removing traversed surfels)
Formalize the embedding 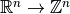
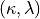 - Jordan for some grid steps)
- Jordan for some grid steps)Let 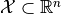 and
and 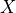 its digitization
its digitization
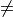 0 but even in this case,
0 but even in this case, 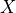 may be empty
may be empty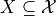
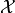 to ensure topological properties on
to ensure topological properties on 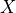 or
or 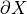
This model was first used to approximate
by
Idea Defined for oriented contours 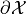
For each intersection 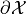 with a grid edge, we select the {closer,inner,outer} grid point
with a grid edge, we select the {closer,inner,outer} grid point
(resp. GIQ -Grid Intersect Quantization-, OBQ -Object Boundary Quantization-, BBQ -Background Boundary Quantization-)
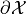 crosses the edge at its mid-point)
crosses the edge at its mid-point)  global Oracle to remove ties
global Oracle to remove ties and
and 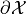
Generic definition
Let 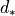 be a metric,
be a metric, 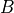 its unit ball and
its unit ball and 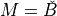
Still bubbles may exist
Following the definition (F,G 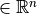 ):
):
prop.
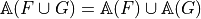
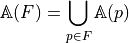
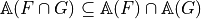
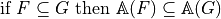
 Allows modeling of digital objects but CSG approach (Constructive Solid Geometry)
Allows modeling of digital objects but CSG approach (Constructive Solid Geometry)
Idea Digitization parametrized by a grid step
E.g. for Gauss digitization
Mathematical results can be obtained with constraints on 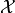 , for example
, for example
thm.
If 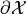 is
is 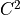 with bounded curvature, there exists a grid step
with bounded curvature, there exists a grid step 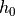 such that for
such that for 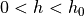 ,
, 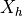 is topologically equivalent to
is topologically equivalent to 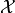
thm.
If 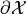 is
is 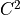 with bounded curvature, the retro-projection from
with bounded curvature, the retro-projection from 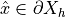 onto
onto 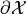 at
at 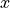 along its normal direction is continuous, mono-valuated and surjective (for
along its normal direction is continuous, mono-valuated and surjective (for 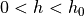 ) and
) and 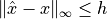 )
)
Question 1 Given a digital object, How to estimate its areas ?
Answer Well, let’s count the number of grid points (unit squares) (estimator denoted E)
Question 2 Is this estimator multigrid convergent ? What is the convergence speed ?
Answer
Let’s consider the estimator 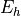 at grid-step h defined on the digitization of the Euclidean shape
at grid-step h defined on the digitization of the Euclidean shape 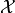 from a given class of shapes
from a given class of shapes
If 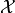 is a finite convex shape, there exists a grid step
is a finite convex shape, there exists a grid step 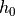 such that for
such that for 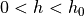 we have:
we have:
[Gauss, Dirichlet]
If 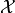 is
is 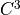 (or finitely piece-wise
(or finitely piece-wise 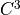 with positive curvature almost everywhere…) then
with positive curvature almost everywhere…) then
[Huxley,…]
Would there be better approaches ?