Contributions aux Cartes Combinatoires et Cartes Généralisées : |
Soutenue publiquement le 23 Septembre 2010 devant le Jury composé de :
| M. Jean-Marc Chassery, Directeur de Recherches, CNRS, GIPSA-Lab | Rapporteur |
| M. Pedro Real, Professeur, Univ. de Seville, Dpt. Math. Appli. | Rapporteur |
| Mme Monique Teillaud, Chargé de Recherches HDR, INRIA, Sophia-Antipolis | Rapporteur |
| M. Luc Brun, Professeur, ENSICAEN, GREYC | Examinateur |
| M. Jean-Michel Jolion, Professeur, INSA de Lyon, LIRIS | Examinateur |
| M. Pascal Lienhardt, Professeur, Univ. Poitiers, XLIM-SIC | Examinateur |
| M. Bernard Péroche, Professeur, Univ. Lyon 1, LIRIS | Examinateur |
La problématique centrale de nos travaux est la représentation et la manipulation d’objets géométriques. Cette problématique se pose dans de très nombreux domaines, comme en modélisation géométrique, en traitement d’images, en rendu réaliste, en simulation d’écoulement de fluides…Dans chacun de ces cas, il est nécessaire d’avoir une structure de données décrivant les objets à manipuler et contenant suffisamment d’information pour les algorithmes utilisés. Cependant, ces informations ne doivent pas être en nombre trop important afin d’être capable de traiter un grand nombre d’objets. Le problème peut donc se résumer, comme souvent en informatique, à trouver le meilleur compromis entre espace mémoire et temps d’exécution des opérations. Mais un troisième problème important se pose dans notre cadre, qui est le pouvoir de modélisation de la structure de données. Ce problème est lié aux informations contenues dans celle-ci. En effet, il faut préciser ce qui est sous-entendu par représenter les objets et les informations, car de nombreuses solutions existent. Les questions auxquelles il va falloir répondre portent sur le type d’objets à représenter et le type de relations entre ces objets. Le choix de la «meilleure» structure de données va en effet dépendre de la dimension, de l’éventuelle régularité des objets, des possibilités pour les objets de se superposer, se toucher par un sommet ou une face…Selon les réponses à ces questions, le choix de la structure de données ne sera pas la même. Enfin, ce choix doit être également guidé par les algorithmes qui vont être utilisés par la suite. Si ces objets doivent uniquement être visualisés, et si nous disposons d’une carte graphique capable d’afficher uniquement des triangles, la meilleure structure de données sera sûrement une simple liste de triangles.
Il existe toute une gamme de structures de données qui ont été définies pour représenter des objets triangulés (triangles en 2D, tétraèdres en 3D, appelés simplexes en nD). Ces éléments de base sont mis en relations par des opérateurs qui vont décrire les relations d’adjacence et d’incidence. Ce type de structure a pour avantage principal d’être simple à mettre en œuvre, de pouvoir être défini en dimension quelconque, et enfin d’être directement utilisable dans des algorithmes de visualisation rapides. En effet, la plupart des moteurs de rendu actuels utilisent des triangles comme primitives de base. De plus, ce type de structure de données peut être mis en relation avec les objets simpliciaux définis en topologie algébrique, et il est alors possible de faire un lien direct entre la structure de données et une partie d’un espace topologique. L’inconvénient principal de ce type de structure se pose lors d’opérations de modification. En effet, certaines opérations produisent des objets non triangulés. Un autre inconvénient est qu’il faut un nombre important de simplexes pour décrire les objets.
Afin de résoudre ces problèmes, plusieurs structures de données ont été définies afin de pouvoir représenter les objets comme assemblage de n’importe quel type de cellules (et pas seulement des triangles). Parmi ces structures, les seules à avoir été formellement définies en dimension quelconque sont des structures proche de la notion de cartes. Ces structures de données ont plusieurs avantages qui justifient leur étude et leur utilisation. Elles sont définies en dimension quelconque à partir d’un seul élément de base. Le fait de ne pas avoir plusieurs structures de données liées entre elles simplifie les algorithmes, les mises à jour, et les développements informatiques. Une carte représente des objets subdivisés en cellules, et décrit toutes les relations d’adjacence et d’incidence entre ces cellules. De ce fait, il est très simple d’associer des informations à n’importe quelle cellule de la subdivision. De plus, l’accès aux différentes relations d’incidence et d’adjacence entre les cellules se fait en temps polynomial en le nombre de cellules dans le voisinage, ce qui donne des algorithmes efficaces. Enfin, le domaine des cartes est clairement défini et le lien formel entre les cartes et les modèles simpliciaux autorise le transfert aux cartes des nombreux travaux existant en topologie algébrique. Pour cette raison, les cartes ne sont pas seulement une structure de données mais bien un modèle mathématique de représentation des objets. De plus, des contraintes de cohérence précises existent et permettent de tester simplement la validité d’une carte.
Ces modèles sont relativement jeunes puisqu’ils ont pris leur essor au début des années 1990, et ils souffrent de ce fait d’un manque de reconnaissance et d’utilisation. De plus, les papiers de références sont très complets, mais du coup également peu abordables pour une personne non initiée, ce qui est une deuxième cause limitant leur utilisation.
Dans ce cadre, nos travaux ont débuté en 1998 tout d’abord dans l’optique d’utiliser les cartes combinatoires afin de décrire les partitions d’images 3D. Nous nous sommes très vite rendu compte qu’il existait un fossé entre les travaux menés en traitement et analyse d’images, et ceux menés en modélisation géométrique. Ce fossé s’expliquait par la manière dont les deux communautés s’étaient intéressées aux cartes : en modélisation, l’objectif est de manipuler et représenter des objets, principalement en 3D, et de définir des opérations de transformation ; en imagerie, les cartes étaient principalement vues comme une extension des graphes planaires représentant l’ordre des arêtes autour des sommets. De ce fait, les habitudes étaient de transposer les algorithmes sur les graphes en algorithmes sur les cartes, ce qui fonctionnait très bien en 2D, mais rendait difficile le passage en dimension supérieure. Après nous être rendu compte de ce problème, nous avons depuis lors essayé de mener de front des activités de modélisation géométrique et de traitement d’images afin que chaque domaine profite des résultats de l’autre, mais également pour que les deux domaines contribuent à de nouvelles avancées autour des cartes.
C’est ce type de réflexion qui nous pousse encore aujourd’hui à réfléchir aux opérations en termes les plus génériques possibles, en dimension quelconque, et sans fixer de contraintes liées à un cadre d’application. C’est dans ce cadre que nous avons défini des opérations de base qui sont les suppressions, contractions, insertions et éclatements. Nous montrons dans ce mémoire que ces opérations peuvent être vues comme une généralisation des opérateurs d’Euler.
Ces opérations sont au cœur de nos travaux et sont le fil conducteur de ce mémoire. En effet, nous avons eu très tôt l’idée de simplifier progressivement un objet à partir d’une carte de base, et d’une application d’une suite de simplifications, en les contrôlant afin de préserver certaines propriétés. Nous avons utilisé ce principe de simplification dans plusieurs problématiques très différentes abordées dans ce mémoire, qui vont de la définition des cartes topologiques, au calcul des groupes d’homologie, en passant par la segmentation d’images ou par des algorithmes de reconstruction de contour discrets.
Mais il n’est pas toujours possible de définir les modèles et opérations de manière générique en nD. En effet, il peut exister des contraintes d’efficacité et nous avons alors besoin d’optimiser un cas particulier par exemple pour des raisons d’espace mémoire. Il existe également des spécificités selon les dimensions. Par exemple en 2D, il est possible d’utiliser le théorème de classification des surfaces afin de définir un algorithme de caractérisation, alors que ce type de théorème n’existe pas en dimension supérieure. Une dernière raison pouvant limiter une définition générique peut tout simplement être la difficulté du passage en dimension supérieure qui fait que nous commençons par étudier les choses en 2D, puis 3D avant d’essayer de généraliser en dimension n.
C’est dans ce cadre que nous avons défini la carte topologique 3D, qui était le sujet initial de notre thèse [Dam01]. Afin d’arriver à cette définition, nous sommes reparti de la dimension 2, en nous reposant les questions de base sur les raisons d’être des modèles existants. Ce type de questionnement nous a amené à proposer la notion de niveau de simplification, qui utilise les opérations de suppression, et c’est cette notion qui nous a permis ensuite de définir de manière relativement simple les cartes topologiques en 3D alors que cela était beaucoup plus difficile de manière directe. Nous avons depuis beaucoup travaillé autour de ces cartes topologiques, en 2D et 3D, afin de définir des opérations de manipulation, comme la fusion ou la découpe de régions, qui nous ont servi ensuite à définir des opérations de segmentation d’images.
Nous avons également étudié différents liens entre les cartes et les invariants topologiques. En effet, il existait très peu de travaux sur le calcul d’invariants topologiques pour les cartes, et aucun ne permettant la mise à jour de ces invariants dans le cadre des opérations de simplification. Nous avons tout d’abord proposé une méthode de calcul de la caractéristique d’Euler-Poincaré, en nous appuyant à nouveau sur l’étude des opérations de base et sur leur impact sur l’évolution des nombres de cellules. Nous avons alors ensuite cherché à calculer d’autres invariants topologiques plus puissants. Cela nous a amené à étudier le calcul des nombres de Betti, puis des groupes d’homologie, pour le moment uniquement en 2D et 3D. Nous avons pu alors utiliser nos algorithmes de calcul des nombres de Betti au sein d’un critère de segmentation d’images 3D, ce qui nous a permis de définir une méthode de segmentation d’images avec contrôle topologique.
Au final, tout ces travaux vont dans la même direction : la définition d’outils performants, génériques, et topologiques de manipulation d’objets 2D, 3D ou nD. Ils ont été en partie réalisés au cours des thèses de Carine Simon, Sébastien Horna, Alexandre Dupas et Romain Goffe, que nous avons co-encadrés. D’autre par, ils ont été réalisés en collaboration avec d’autres chercheurs français: Olivier Alata, Sylvie Alayrangues, Eric Andres, Denis Arrivault, Mehdi Baba-ali, Fabien Baldacci, Yves Bertrand, Camille Bihoreau, Pascal Bourdon, Achille Braquelaire, Luc Brun, David Coeurjolly, Martine Dexet-Guiard, Jean-Philippe Domenger, Christophe Fiorio, Laurent Fuchs, Colin De La Higuera, Jean-Christophe Janodet, Jacques-Olivier Lachaud, Pascal Lienhardt, David Marcheix, Daniel Meneveaux, Christian Olivier, Samuel Peltier, Patrick Resch, Emilie Samuel, Xavier Skapin, Christine Solnon, Frédéric Vidil ; et étrangers : Yll Haxhimusa, Adian Ion, Walter G. Kropatsch. Enfin, une partie de ces problématiques ont été étudiées dans le cadre du projet ANR Fogrimmi de Janvier 2007 à Décembre 2010, dans lequel nous avons été porteur pour le laboratoire XLIM-SIC. Ces différents travaux montrent chacun, à différents niveaux, l’intérêt d’utiliser des cartes dans différentes problématiques, et nous espérons qu’ils participeront à promouvoir leur diffusion. Nous espérons également que ce mémoire œuvrera dans ce sens en regroupant en un même endroit les notions principales autour des cartes.
Le plan de ce mémoire est le suivant. Tout d’abord nous présentons au chapitre 2 les notions de base de la topologique algébrique, les modèles existants, puis nous présentons en détails les cartes combinatoires et les cartes généralisées. Ce chapitre est l’occasion d’éclaircir certains points, et de compléter des notions qui manquaient jusqu’alors. Le chapitre 3 présente les quatre opérations de base que nous avons définies en dimension quelconque dans le cadre des cartes généralisées : la suppression, son opération duale qui est la contraction, et les opérations inverses qui sont l’insertion et l’éclatement. Nous présentons également l’opération de décalage d’arête. Le chapitre 4 présente la carte topologique en 2 et 3 dimensions. C’est un modèle décrivant la partition d’une image en régions et qui est basé sur les cartes combinatoires. Sa définition utilise les opérations de base, qui sont contrôlées afin de garantir l’absence de perte d’information. Le chapitre 5 introduit les pyramides généralisées qui sont une extension hiérarchique des cartes généralisées, et donne les principales définitions utiles afin de retrouver les informations au sein de ce type de pyramide. Nous présentons au chapitre 6 des algorithmes de calcul d’invariants topologiques utilisant les cartes. Nous nous sommes intéressés à la caractéristique d’Euler-Poincaré, aux nombres de Betti, et aux groupes d’homologie. Le chapitre 7 illustre l’application de ces différents travaux dans quelques utilisations que nous avons pu faire. Pour le moment, nous avons principalement appliqué nos méthodes dans un projet de reconstruction de complexes architecturaux, et dans des algorithmes de segmentation d’images autorisant un contrôle topologique. Enfin, le chapitre 8 conclut ce mémoire et présente mon programme de recherche pour les années à venir.
La topologie algébrique (anciennement appelée topologie combinatoire) est une branche des mathématiques cherchant à étudier les espaces topologiques en leur associant un objet algébrique (groupe, espace vectoriel, …) dont les propriétés servent à déterminer un certain nombre d’invariants caractérisant la topologie de l’espace initial. Deux outils ont été beaucoup utilisés afin de réaliser cette étude : le groupe fondamental ou plus généralement la théorie de l’homotopie, et le groupe d’homologie ou groupe de co-homologie.
Le problème de la théorie de l’homotopie est que les groupes d’homotopie sont difficilement exploitables de manière simple. Une difficulté importante provient de la représentation de ces groupes qui est réalisée par un ensemble de mots et des relations sur ces mots. De ce fait, savoir si deux groupes sont isomorphes revient à résoudre le problème du mot1. Or, ce problème a été montré indécidable [Nov55] ce qui implique que le problème général de savoir si deux groupes fondamentaux sont isomorphes l’est également2. Pour s’affranchir de ce problème, nous nous intéressons donc ici à la théorie de l’homologie dans laquelle les représentations des groupes et les algorithmes de calcul peuvent être envisagés. Pour cette raison, nous n’étudions donc pas du tout par la suite le groupe fondamental mais uniquement les groupes d’homologie et les notions associées.
Dans nos travaux, nous nous intéressons aux partitions d’espaces en cellules comme les complexes simpliciaux ou les complexes cellulaires. Intuitivement, nous souhaitons représenter un sous-espace de ℝn de manière combinatoire c’est-à-dire en «oubliant» la forme. Il existe différentes manières de faire selon les propriétés des objets représentés (par exemple orientables ou non, simpliciaux ou cellulaires…), mais dans tous les cas, il est important de pouvoir contrôler la validité des objets représentés. C’est pour cette raison que la partie la plus importante dans la définition de modèles combinatoires concerne leurs contraintes de cohérence. Ce sont elles qui vont garantir que l’objet combinatoire correspond bien à son équivalent topologique. Elles peuvent également autoriser la vérification algorithmique qu’un objet donné est valide ou non. Dans ce cadre, nous nous sommes plus particulièrement aux cartes combinatoires et cartes généralisées, deux modèles permettant de représenter des partitions cellulaires nD, et autorisant un accès efficace aux cellules et aux relations entre celles-ci.
L’objectif de ce chapitre est de centraliser les principales notions autour des cartes combinatoires et généralisées. La plupart de ces notions sont issues des deux papiers de références [Lie91, Lie94] ainsi que du chapitre de livre [LFB07] ; les notions préliminaires sont souvent issues des livres [Spa66, Cro78, Mun84, Hat02] ; certains éléments proviennent de la lecture des thèses [Elt94, Lan95, Ala05, Pel06, Fav09, Dup09]. Certaines notions concernant le dual et les cartes ouvertes sont «re-découvertes» dans ce chapitre : soit car les notions originales ne correspondent pas exactement à celles utilisées ; soit car elles manquaient d’explications, d’illustrations ou de preuves. J’espère que ce chapitre pourra servir de référence pour un lecteur cherchant des explications précises sur les cartes, en regroupant en un même endroit les principales notions portant sur les cartes combinatoires et généralisées.
Ce chapitre est organisé de la manière suivante. Nous présentons Section 2.1 les notions de base de topologie algébrique, les notations utilisées dans ce mémoire, et quatre modèles topologiques classiques qui sont les complexes simpliciaux, les complexes cellulaires, les complexes simpliciaux abstraits et les complexes cellulaires abstraits. Nous introduisons Section 2.2 des structures combinatoires permettant de représenter ces modèles, ou certaines sous-classes, et décrivant directement les relations entre les éléments : les ensembles semi-simpliciaux qui sont une sous-classe des complexes simpliciaux ; les cartes combinatoires, en rappelant l’historique de leur définition en 2D, et les cartes généralisées, qui permettent de représenter des sous-classes de complexes cellulaires orientables pour les cartes combinatoires, et quelconques pour les cartes généralisées. Nous détaillons également les cartes combinatoires ouvertes, une extension des cartes pouvant représenter des complexes ouverts. La Section 2.3 détaille le lien entre les cartes et les ensembles semi-simpliciaux, ce qui permet de transposer des définitions basées sur les complexes simpliciaux vers les complexes cellulaires, comme par exemple le calcul de la caractéristique d’Euler-Poincaré.
Nous commençons par présenter quelques notions de base de topologie algébrique qui seront utiles dans la suite de ce mémoire.
Soit un ensemble E, une famille d’ensembles sur E (ou famille de sous-ensembles de E) est un ensemble de sous-ensembles de E. P(E) est l’ensemble des parties de E . C’est une famille d’ensembles sur E définie par P(E)={X ⊆ E}. Une partition P de E est une famille d’ensembles sur E telle que les éléments de P sont deux à deux disjoints et forment un recouvrement de E (cf. Def. 1).
Le couple (X,τ) est appelé espace topologique. Les éléments de X sont appelés les points, et les éléments de τ sont appelés les ouverts de la topologie. Un sous-ensemble de X est dit fermé si son complémentaire dans X est ouvert. Chaque élément de τ peut être ouvert, fermé, les deux à la fois, ou encore ni ouvert ni fermé. Par définition, ∅ et X sont toujours des ouverts et des fermés. Soit X un ensemble d’éléments, la topologie discrète sur X est la topologie (X,P(X)). De façon intuitive, c’est la topologie dans laquelle chaque point est «isolé». En effet, dans cette topologie, chaque point de X est à la fois ouvert et fermé. Une notion fondamentale en topologie est la notion de voisinage. Soit x ∈ X. V ⊆ X est un voisinage de x dans la topologie (X,τ) si il existe un ouvert inclus dans V contenant x. Le voisinage d’un point n’est jamais vide car X est un voisinage de tout point de X. Un espace topologique est dit séparé, ou espace de Hausdorff, si pour deux points distincts x et y quelconques, il existe un voisinage de x et un voisinage de y disjoints.
Bn est la boule unité nD : c’est l’ensemble des points x de ℝn tel que ||x|| ≤ 1 (avec si x=(x1,…,xn), ||x||=√x12+… xn2). La boule unité ouverte nD h(B)n est l’ensemble des points x de ℝn tel que ||x|| < 1. La demi-boule unité consiste à restreindre une coordonnée (la première dans ce qui suit) aux nombres positifs ou nuls. B1/2n = {x=(x1,…,xn) | ||x|| ≤ 1 et x1 ≥ 0}, et enfin la demi-boule unité ouverte3 est h(B1/2)n = {x=(x1,…,xn) | ||x|| < 1 et x1 > 0}. Sn−1 est la sphère unité nD : c’est l’ensemble des points x de ℝn tel que ||x|| = 1.
Par exemple Bn est une variété fermée, dont le bord est Sn−1, tandis que h(B)n est une variété ouverte, donc sans bord.
Une variété topologique nD est dite orientable s’il est possible de définir une direction «gauche» et «droite» globalement en tout point de la variété. Elle est dite non-orientable sinon. Deux exemples de 2-variétés non orientables sont présentés Fig. 2.1 : le ruban de Möbius à la Fig. 2.1.1, et la bouteille de Klein à la Fig. 2.1.1.
Après cette introduction aux notions topologiques de base, nous introduisons maintenant les notations et outils mathématiques que nous utilisons par la suite.
Soit E un ensemble non vide. Soit f une fonction de E dans E. f est une permutation sur E si c’est une bijection de E dans E. f est une involution sur E si c’est une bijection de E dans E telle que f=f−1, ce qui est équivalent à f ∘ f = IdE (une involution est donc une permutation particulière ; de ce fait, lorsque nous considérerons un ensemble de permutations, il pourra contenir des involutions). Soit e ∈ E, e est un point fixe de f si f(e)=e. Soit X ⊆ E, nous notons f(X)={f(x)|x ∈ X}. IdE est la fonction identité de E dans E .
Une relation d’ordre R pour un ensemble E est une relation binaire réflexive (x R x) transitive (x R y et y R z ⇒ x R z) et antisymétrique (x R y et y R x ⇒ x=y). Si pour tout couple d’éléments x,y dans E2, x et y sont comparables par R, la relation d’ordre est dite totale. Sinon elle est dite partielle.
Soit Φ={f1,…,fk} un ensemble de permutations sur un même ensemble E, et e ∈ E. Nous utilisons parfois la notation anglaise e f1 … fk pour fk(…(f1(e))). ⟨Φ⟩ est le groupe de permutations engendré par Φ. C’est l’ensemble des permutations qu’il est possible d’obtenir de Φ par application de la composition et de l’inverse. Ce groupe de permutations permet de définir la notion d’orbite d’un élément de E.
L’orbite d’un élément est l’ensemble des éléments de E qu’il est possible d’atteindre par application, à partir de e, de n’importe quelle suite de fi et fi−1. Étant donnée un ensemble de permutations Φ, nous notons z(⟨Φ⟩) le nombre d’orbites distinctes d’éléments de E, c’est-à-dire |{⟨Φ⟩(e)|e∈ E}| (cf. Section 2.2.3 pour des exemples d’orbites).
Un complexe simplicial [Spa66, Ago76, PBCF93, Hat02] peut être vu de manière constructive comme un espace topologique obtenu en collant entre eux des simplexes.
Un simplexe s de dimension n est un n-polyèdre5 formé par l’enveloppe convexe d’un ensemble P de n+1 points de ℝn affinement indépendants. Un sommet est un 0-simplexe, un segment un 1-simplexe, un triangle un 2-simplexe et un tétraèdre un 3-simplexe. Un n-simplexe est homéomorphe à la boule Bn. L’enveloppe convexe de n’importe quel sous-ensemble non vide de P est une face de s (donc une face est elle-même un simplexe). Un simplexe f est une coface de s si s est une face de f. Deux simplexes sont incidents si l’un est une face de l’autre, et deux i-simplexes s1 et s2 sont adjacents s’il existe un simplexe qui soit une face de s1 et une face de s2.
Par définition des simplexes comme enveloppe convexe de points affinement indépendants, un simplexe a nécessairement une géométrie linéaire (c-à-d chaque 1-simplexe est un segment de droite), et ne peut pas avoir de dégénérescence6. De plus, la définition d’un complexe simplicial interdit la présence de multi-incidence (c-à-d le cas de deux i-simplexes ayant pour intersection plus d’un simplexe. En effet, dans ce cas, l’intersection n’est pas une face des deux simplexes).
La Fig. 2.2 montre un exemple et un contre-exemple de complexe simplicial. Pour la Fig. 2.1.2, le complexe est composée de cinq sommets numérotés de 1 à 5, de six 1-simplexes et de deux 2-simplexes (donc le complexe contient en tout 13 simplexes). Il est facile de vérifier sur cet exemple que l’intersection de n’importe quel couple de simplexes est un simplexe ou est vide. Par contre, l’ensemble présenté Fig. 2.1.2 n’est pas un complexe simplicial car l’intersection des deux triangles n’est pas une face commune.
[a][b]
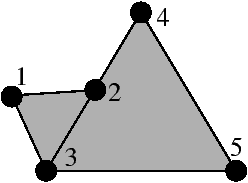
Figure 2.2: Un exemple (a) et un contre-exemple (b) de complexe simplicial. (a) L’ensemble contenant les deux 2-simplexes de sommets {a,b,c} et {a,b,d}, le 1-simplexe de sommets {b,e}, et toutes leurs faces est un complexe simplicial contenant cinq sommets, six 1-simplexes et deux 2-simplexes. (b) L’ensemble contenant les deux 2-simplexes et toutes leurs faces n’est pas un complexe simplicial car l’intersection des deux 2-simplexes de sommets {1,2,3} et {3,4,5} est l’arête de sommets {2,3} qui n’est pas une face du simplexe de sommets {3,4,5}.
La Def. 10 de pseudo-variétés7 permet de vérifier de manière combinatoire si un complexe simplicial représente une variété [Sti80].
Mais cette notion de pseudo-variété n’est pas équivalente à la notion de variété. Considérons l’exemple de la Fig. 2.3. C’est un ensemble de triangles formant une surface homémorphe à la sphère S2, dans lequel deux sommets de la surface sont identifiés. Ce complexe simplicial est une pseudo-variété (car chaque 1-simplexe est bien la face d’au plus deux 2-simplexes), mais n’est pas une variété car le voisinage du point résultat de l’identification n’est pas homéomorphe à la boule ouverte h(B2) ni à la demi-boule ouverte h(B1/2)2.
Les complexes simpliciaux ont été étendus pour pouvoir utiliser des éléments de base plus généraux que les simplexes : ce sont les CW-complexes (appelés parfois complexes cellulaires) défini par [Whi49]. Il existe de nombreux travaux autour des CW-complexes et leur étude sort du cadre de ce travail. Nous introduisons simplement ici les notions intuitives. De manière informelle, un CW-complexe est obtenu en collant entre elles des cellules de base qui sont homéomorphes à des boules Bn, de telle sorte que le collage respecte des propriétés de continuité. Plus précisément, un CW-complexe est un espace de Hausdorff X, avec une décomposition de X en cellules, et une fonction continue entre chaque n-cellule et Bn qui doit vérifier des propriétés supplémentaires. Il faut noter que cette définition des CW-complexes rend difficile la mise en œuvre de structure de données pour les manipuler de par la présence de la fonction continue et de ses propriétés. La Def. 10 de pseudo-variété est étendue au CW-complexes en remplaçant les simplexes par des cellules.
Un complexe simplicial abstrait (CSA) correspond à l’information purement combinatoire qu’il est possible d’extraire d’un complexe simplicial.
Chaque élément A de K est un simplexe. Un sous-ensemble de A étant une face de A, cette définition peut se reformuler en disant que chaque face de chaque simplexe appartient au complexe. La dimension d’une face A est |A|−1. La dimension du complexe est la plus grande dimension d’un simplexe de K. Un simplexe est dit principal s’il n’est la face d’aucun simplexe du complexe.
À tout complexe simplicial abstrait peut être associé un complexe simplicial. Ce complexe simplicial est appelée la réalisation géométrique du complexe simplicial abstrait. Il faut noter que cette réalisation géométrique est unique à isomorphisme près. Lors de l’association de la géométrie à un complexe simplicial abstrait, il faut vérifier que les contraintes géométriques du complexe simplicial sont satisfaites. De manière réciproque, à chaque complexe simplicial peut être associé un complexe simplicial abstrait. Il suffit d’énumérer tous les simplexes par leurs ensembles de sommets pour construire le complexe simplicial abstrait correspondant.
Prenons comme exemple le complexe simplicial abstrait {{a,b,c},{a,b,d},{b,e}, {a,b},{a,c},{b,c},{a,d},{b,d},{a},{b},{c},{d},{e}}. Les trois premiers éléments de cet ensemble sont les simplexes principaux. L’ensemble des sommets est {a,b,c,d,e}. {a,b} est une face de dimension 1 de {a,b,c}, et la dimension du complexe est 2. Le complexe simplicial de la Fig. 2.1.2 est une réalisation géométrique de ce complexe simplicial abstrait.
Considérons maintenant le CSA {{a,b,c},{c,d,e},{a,b},{a,c},{b,c},{c,d},{d,e},{c, e},{a},{b},{c},{d},{e}}. Il est possible d’associer aux sommets a,b,c,d,e de ce CSA les sommets 1,2,3,4,5 de la Fig. 2.1.2 (dans l’ordre). Avec cette association, chaque simplexe du CSA correspond à un simplexe du complexe simplicial. Mais ce n’est pas une réalisation géométrique de ce CSA car dans ce cas les contraintes géométriques du complexe simplicial ne sont pas vérifiées. La Fig. 2.4 montre un complexe simplicial qui est la réalisation géométrique de ce CSA.
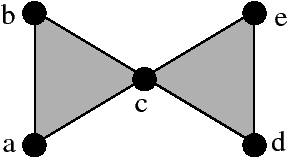
Figure 2.4: Un complexe simplicial qui est la réalisation géométrique du complexe simplicial abstrait {{a,b,c},{c,d,e},{a,b},{a,c},{b,c},{c,d},{d,e},{c,e},{a},{b},{c},{d}, {e}}.
Les complexes cellulaires abstraits [Mun84, Kle00, KR04, Kov08] étendent les complexes simpliciaux abstraits pour ne plus considérer uniquement des simplexes mais des cellules quelconques. Par rapport aux complexes simpliciaux abstraits, il faut désormais ajouter la notion de dimension qui était avant implicite de par la nature régulière des simplexes, et expliciter la relation de face entre les cellules.
Les éléments de C sont les cellules du complexe, et la relation ≼ est la relation de face. Les faces d’une cellule c sont toutes les cellules c′ tel que c′ ≼ c. Cette relation permet de définir la notion d’incidence et d’adjacence. Deux cellules sont incidentes si l’une est la face de l’autre, et deux cellules c et c′ sont adjacentes si dim(c)=dim(c′) et ∃ f ∈ C, tel que f est une face de c et une face de c′.
De manière similaire aux complexes simpliciaux abstraits, la dimension d’un complexe cellulaire abstrait C est la plus grande dimension d’une cellule de C, et une cellule est dite principale si elle n’est la face d’aucune cellule du complexe.
Un invariant topologique est une propriété qui se conserve par homéomorphisme : les invariants topologiques de deux objets homéomorphes sont égaux. La dimension de l’objet ou son nombre de composantes connexes sont deux exemples d’invariants topologiques.
La caractéristique d’Euler-Poincaré est le plus connu des invariants topologiques. Pour un complexe cellulaire, elle se définit simplement par la somme alternée du nombre de cellules de chaque dimension (cf. Def. 13). Comme cette caractéristique est un invariant topologique, elle ne dépend pas de la décomposition cellulaire. De plus, elle est réunion-additive, c’est-à-dire que la caractéristique d’Euler-Poincaré d’un objet qui est l’union disjointe de deux objets est la somme des deux caractéristiques de ces objets.
Nous présentons Fig. 2.5 un exemple de calcul de la caractéristique d’Euler-Poincaré pour deux subdivisions différentes d’un tore. Dans le premier cas, le complexe cellulaire est composé de neuf 0-cellules, dix-huit 1-cellules et neuf 2-cellules. χ=9−18+9=0. Dans le second cas, le complexe cellulaire est composé de seize 0-cellules, trente-deux 1-cellules et seize 2-cellules. χ est donc à nouveau égale à 0.
Les nombres de Betti (notés bi pour le nombre de Betti en dimension i) sont des invariants topologiques qui, intuitivement, comptent le nombre de «trous» dans chaque dimension. Par exemple, pour un objet 3D, b0 compte le nombre de composantes connexes, b1 compte le nombre de tunnels (appelés parfois anses) et b2 compte le nombre de cavités (appelées parfois trous). Pour un objet nD, les nombres de Betti bk pour k>n sont tous égaux à zéro. Pour l’exemple de la Fig. 2.1.4, b0=1, b1=3 et b2=2, et pour celui de la Fig. 2.1.4, b0=2, b1=3 et b2=1.
[a][b]

Figure 2.6: Nombres de Betti en dimension 3. Les objets représentés ici sont «pleins». (a) Complexe cellulaire 3D composé d’une composante connexe : b0=1 ; de trois tunnels : b1=3 ; et de deux cavités: b2=2 : χ=1. (b) Complexe cellulaire 3D composé de deux composantes connexes : b0=2 ; de trois tunnels : b1=3 ; et d’une cavité : b2=1 : χ=1.
La caractéristique d’Euler-Poincaré peut également être définie comme la somme alternée des nombres de Betti (Def. 14), et les deux définitions sont équivalentes (cf. [Hat02]).
Par cette définition, deux complexes cellulaires ayant mêmes nombres de Betti ont la même caractéristique d’Euler-Poincaré. Mais l’inverse n’est pas vrai : deux complexes ayant la même caractéristique d’Euler-Poincaré n’auront pas forcément les mêmes nombres de Betti comme nous pouvons le voir sur l’exemple de la Fig. 2.6. De ce fait, les nombres de Betti sont des invariants topologiques «plus puissants» que la caractéristique d’Euler-Poincaré car ils permettent de différencier plus de complexes cellulaires que la caractéristique d’Euler-Poincaré.
Les nombres de Betti sont liés aux groupes d’homologie, un autre invariant topologique. Plus précisément, le nombre de Betti bi est le rang du ième groupe d’homologie. Cet invariant est encore plus puissant que les nombres de Betti car il décrit les trous des objets en terme de cycles de cellules et pas uniquement en les comptant. De ce fait, il représente les torsions de l’objet (les parties d’un objet non orientable qui ont été recollées «à l’envers») qui ne sont pas prises en compte dans les nombres de Betti. Par contre la caractéristique d’Euler-Poincaré et les nombres de Betti sont plus simples à manipuler car ils sont définis directement comme des valeurs numériques.
En 2D, le Théorème 1 de classification des surfaces (qui date des années 1860, mais qui est donné par exemple dans [Lee00]) prouve que toute surface peut se caractériser par son orientation et sa caractéristique d’Euler-Poincaré.
La somme connexe de deux surfaces M et N, notée M#N, est obtenue en enlevant un disque (homéomorphe à B2) de chacune des deux surfaces, et en recollant les deux surfaces le long des deux bords créés. La caractéristique d’Euler-Poincaré de la somme connexe est calculée à partir de la somme des caractéristiques de chaque surface moins les deux disques : χ(M#N)=χ(M)+χ(N)−2.
Les deux premières familles du théorème de classification sont les surfaces orientables. Dans ces deux cas, le nombre g, appelé le genre, est le nombre de tores utilisés dans la somme connexe (donc 0 dans le cas de la sphère). Comme la sphère et le tore ont comme caractéristique d’Euler-Poincaré respectivement 2 et 0, en utilisant la formule précédente sur la caractéristique d’Euler-Poincaré d’une somme connexe, nous obtenons que χ(c)=2−2g (dans le cas d’un tore, cf. exemple de la Fig. 2.5, nous avons χ=0 et g=1).
Dans le troisième cas, la surface est non-orientable. La caractéristique d’Euler-Poincaré d’un plan projectif est 1, et en utilisant la formule sur la caractéristique d’Euler-Poincaré d’une somme connexe, nous obtenons que χ(c)=2−k.
De ce fait, toute surface 2D fermée est déterminée de manière unique par sa caractéristique d’Euler-Poincaré et son orientabilité, ce qui classifie totalement les surfaces 2D fermées. Cette classification s’étend aux surfaces ouvertes en ajoutant comme caractéristique le nombre de bords. Il faut noter que ce type de classification n’existe pas en dimension supérieure dans le cas général.
Manipuler les complexes simpliciaux ou cellulaires décrits dans la section précédente revient à manipuler des ensembles et à utiliser des opérations ensemblistes. De ce fait, les algorithmes permettant de retrouver les relations entre les cellules (comme par exemple toutes les cellules adjacentes à une cellule donnée) sont coûteux car non limités aux voisinages des cellules (pour les cellules adjacentes à une cellule donnée, nous devons parcourir toutes les cellules de l’ensemble).
Pour ces raisons, plusieurs travaux se sont intéressés à la définition de structures combinatoires permettant de représenter ces modèles. Pour chaque structure, l’important est d’être capable de représenter les cellules et les relations d’adjacence et d’incidence entre ces cellules, mais également d’avoir une interprétation topologique de la structure par rapport à l’espace représenté. C’est pour cette raison que des contraintes de cohérence sont définies.
Un ensemble semi-simplicial [May67, FP90, EL94, Lan95, LL95] est un modèle algébrique représentant des simplexes et des relations d’incidence. Il est possible d’associer un ensemble semi-simplicial à tout complexe simplicial, mais le contraire n’est pas vrai. En effet, un ensemble semi-simplicial présentant des relations de multi-incidence ne pourra pas être représenté par un complexe simplicial contenant la relation de multi-incidence (cf. exemple Fig. 2.2.1). La réalisation géométrique d’un tel ensemble sera alors un CW-complexe.
La Def. 15 donne la définition des ensembles semi-simpliciaux qui, contrairement aux complexes simpliciaux, contiennent explicitement les relations de face entre les simplexes.
Les éléments de Kp sont les simplexes de dimension p (ou p-simplexes), et les applications dip sont les opérateurs de face des simplexes donnant pour chaque p-simplexe les (p−1)-simplexes de son bord. Il y a p+1 (p−1)-simplexes dans le bord d’un p-simplexe, chacun est obtenu par un dip différent, pour i allant de 0 à p. De manière générale et afin de simplifier les notations, dip est parfois noté di. Les relations djp−1(dip(s))=di−1p−1(djp(s)) garantissent la cohérence de la structure simpliciale. Par exemple, ces relations garantissent qu’un triangle est bordé par trois sommets. Intuitivement, ces relations indiquent que le simplexe obtenu par le chemin djp−1(dip) est le même que celui obtenu par le chemin di−1p−1(djp). Sans ces contraintes, un triangle pourrait avoir jusqu’à six sommets dans son bord. Il faut noter que les ensembles semi-simpliciaux sont sans opérateur de dégénérescence10 contrairement aux ensembles simpliciaux (que nous ne détaillons pas ici).
Nous pouvons voir un exemple d’ensemble semi-simplicial Fig. 2.2.1, et vérifier que les contraintes de cohérence sont satisfaites : par exemple d1(d2(1))=d1(d1(1)) et d0(d2(1))=d1(d0(1)).
[a][b]
[c]
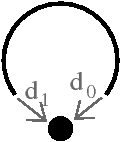
Figure 2.7: Exemple de complexe simplicial et d’ensemble semi-simplicial. (a) Un complexe simplicial C composé de cinq 0-simplexes (étiquetés de a à e), six 1-simplexes et deux 2-simplexes. (b) Un ensemble semi-simplicial correspondant à C. Les deux 2-simplexes sont numérotés 1 et 2. (c) Un ensemble semi-simplicial qui ne correspond pas à un complexe simplicial à cause de la multi-incidence.
Le bord d’un i-simplexe s est l’ensemble des j-simplexes s′, avec 0≤ j < i, tels que s′ est une face de s. L’étoile est la relation inverse : l’étoile d’un i-simplexe s est l’ensemble des j-simplexes s′, avec i< j ≤ n, tels que s est une face de s′.
Les premiers travaux autour des cartes combinatoires [Edm60, Tut63, Jac70, Cor73, Cor75] avaient pour objectif de définir une structure de données permettant de manipuler un graphe planaire11 plongé12 sur un plan. Ces travaux ont été réalisés au sein de la communauté de la théorie des graphes dans le cadre d’études de propriétés des graphes planaires. Nous présentons ici ces travaux uniquement dans le but de donner une vision de l’historique des cartes, car ces notions sont maintenant comprises dans la définition nD des cartes combinatoires présentées Section 2.2.3.
Lorsqu’un graphe est plongé dans le plan, les arêtes peuvent être ordonnées autour des sommets et il est possible alors de définir une application donnant pour chaque arête, l’arête suivante autour d’un sommet. Mais un problème se pose : une même arête a deux successeurs différents, un pour chacun de ses deux sommets. La solution à ce problème consiste à découper chaque arête du graphe en deux éléments (appelés donc demi-arêtes ou brins). De ce fait, un brin étant incident à un seul sommet, il a un unique successeur. Par contre, il faut ajouter une relation entre les deux brins issus de la même arête. La relation donnant, pour un brin, son brin successeur autour d’un sommet a été appelée σ (s pour sommet) et celle donnant l’autre brin issu de la même arête a été appelée α (a pour arête). Comme chaque arête est représentée par deux brins, appliquer α deux fois à partir d’un brin b redonne le brin b : α est une involution. Par contre, σ est une permutation : à partir d’un brin b, appliquer σ plusieurs fois (mais pas nécessairement deux fois) permet de revenir sur b.
Une carte combinatoire 2D est donc un ensemble de brins B plus une involution α et une permutation σ, notée C=(B,α,σ). Par construction, le nombre de brins d’une carte combinatoire est le double du nombre d’arêtes du graphe. Il faut noter que les sommets du graphe ne sont pas représentés explicitement dans la carte combinatoire. En effet, un sommet est l’ensemble des brins obtenus en partant d’un brin b et en utilisant l’application σ jusqu’à retomber sur le brin de départ b.
Comme une carte combinatoire représente un graphe planaire plongé, les cycles d’arêtes délimitent des zones de l’espace appelées faces. Étant donné un brin b, la face déterminée par b s’obtient en utilisant σ ∘ α (noté ϕ, f pour face) jusqu’à retomber sur le brin de départ b. Les faces parcourues à l’aide de la permutation ϕ sont toutes parcourues avec la même orientation, mais le choix d’une orientation est arbitraire. De plus, il faut noter la présence d’une face infinie (appelée également face externe ou face englobante) qui «entoure» les autres faces.
La Fig. 2.8 présente un exemple de graphe planaire (Fig. 2.2.2), et la carte combinatoire 2D correspondante qui peut être dessinée de deux manières différentes (Fig. 2.2.2 où deux brins en relation par α sont dessinés comme une arête du graphe, et Fig. 2.2.2 où deux brins en relation par α sont dessinés comme deux segments parallèle). Le sommet d du graphe correspond à l’ensemble de brins {6,8,14,15} obtenu par exemple à partir du brin 6 en utilisant l’application σ; la carte de cet exemple comporte sept sommets. La face délimitée par les sommets (c,d,f,e) du graphe correspond à l’ensemble de brins {2,4,6,7} et s’obtient par exemple à partir du brin 2 en tournant autour de la face à l’aide de ϕ : ϕ(2)=7, ϕ(7)=6, ϕ(6)=4 et ϕ(4)=2. Sur cet exemple, le choix d’orientation fait que l’intérieur de la face se trouve à droite de l’arête courante, en suivant cette arête selon son orientation. La face {1,3,10,12,14,16,18} est la face infinie. Notez que la règle d’orientation est vérifiée même pour la face infinie : l’intérieur de la face, qui se trouve à l’extérieur de l’objet, se situe bien à main droite de chaque arête de la face. Cette carte contient quatre faces : trois faces bornées et une face infinie.
[a][b]
[c]
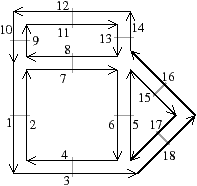
Figure 2.8: La représentation d’un graphe planaire à l’aide d’une carte combinatoire. (a) Un graphe planaire plongé dans le plan. (b) La carte combinatoire correspondante. Les brins sont numérotés de 1 à 18. La relation σ est représentée par les flèches grises (par exemple σ(1)=7), et deux brins en relation par α sont dessinés comme un seul segment avec une barre perpendiculaire séparant les deux éléments (par exemple α(1)=2). (c) Une seconde manière de dessiner la même carte combinatoire. Un brin est représenté par une flèche, deux brins en relation par α sont dessinés parallèlement, avec des orientations opposées (par exemple α(1)=2), et reliés par un petit segment gris. Deux brins en relation par ϕ sont dessinés de manière consécutive (par exemple ϕ(1)=3). Ce type de dessin fait apparaître plus clairement les faces de la carte, alors que la première manière fait apparaître plus clairement les sommets.
Une carte combinatoire est définie à l’aide d’une involution et une permutation, l’autre permutation étant implicite car c’est la composition des deux premières applications. Il existe deux cartes combinatoires duales l’une de l’autre selon que la permutation de la carte représente les sommets σ (comme dans le paragraphe et l’exemple précédent) ou ϕ comme dans l’exemple de la Fig. 2.9. Plus précisément, soit C=(B,α,σ) une carte combinatoire, la carte combinatoire duale est C=(B,α,ϕ). Ces cartes sont duales car les sommets de l’une correspondent aux faces de l’autre et réciproquement.
La Fig. 2.9 montre le graphe dual et la carte combinatoire duale du graphe et de la carte présentés Fig. 2.8. La carte est composée de quatre sommets et de sept faces, car la carte de la Fig. 2.2.2 est composée de sept sommets et de quatre faces. Nous pouvons vérifier sur cet exemple que σ de la carte duale égale ϕ de la carte initiale et réciproquement. Il faut faire attention à distinguer les deux représentations graphiques d’une même carte combinatoire (comme par exemple les deux cartes Fig. 2.2.2 et Fig. 2.2.2) et les deux cartes combinatoires duales (comme par exemple les deux cartes Fig. 2.2.2 et Fig. 2.2.2) qui ne sont pas les mêmes cartes.
[a][b]
[c]
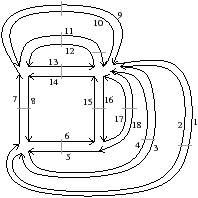
Figure 2.9: Carte combinatoire duale. (a) Le multi-graphe dual (en noir) du graphe de la Fig. 2.2.2 (dessiné ici en gris). Ce multi-graphe s’obtient en mettant un sommet par face du graphe initial et en mettant autant d’arêtes entre deux sommets que le nombre de fois que les deux faces correspondantes dans le graphe initial sont voisines. (b) La carte combinatoire correspondante qui est donc la carte duale de la carte présenté Fig. 2.2.2. (c) La même carte dessinée de la seconde manière.
Bien que définies initialement comme une représentation des graphes planaires plongés, les cartes combinatoires 2D permettent de représenter toute subdivision de n’importe quelle surface orientable fermée. Dans le cas des graphes planaires plongés, ce sont des subdivisions de la sphère (et non du plan à cause de la face infinie). Mais une carte combinatoire 2D peut représenter une subdivision d’un tore comme sur l’exemple de la Fig. 2.2.2 ou d’un tore à deux trous comme sur l’exemple de la Fig. 2.2.2 (de manière générale, le théorème de classification des surfaces dit que toute surface orientable fermée est homéomorphe soit à une sphère soit à un tore à k trous). Étant donnée une carte combinatoire 2D, le type de la surface correspondante peut se calculer en utilisant la caractéristique d’Euler-Poincaré.
[a][b]
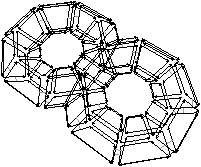
Figure 2.10: Deux exemples de cartes combinatoires 2D n’étant pas des subdivisions de la sphère (les nombres de cellules sont calculés par programme). (a) Une subdivision d’un tore. La carte est composée de 32 sommets, 64 arêtes et 32 faces : χ=0. (b) Une subdivision d’un tore à deux trous. La carte est composée de 82 sommets, 148 arêtes et 64 faces : χ=−2.
Enfin, une carte combinatoire 2D est équivalente à la structure des demi-arêtes [Wei85, Wei88] (en anglais half-edges) très utilisée en modélisation géométrique et en géométrie algorithmique. Il existe en effet une bijection entre les éléments de la structure en demi-arêtes (les demi-arêtes) et les éléments de la carte combinatoires 2D (les brins). Chaque demi-arête est associée avec la demi-arête suivante (ϕ dans la carte), éventuellement la demi-arête précédente (ϕ−1 dans la carte), et la demi-arête opposée (α dans la carte). Différentes implémentations des demi-arêtes ajoutent des relations liant chaque demi-arête avec le sommet incident, et/ou avec la face incidente. C’est également possible de manière équivalente pour les cartes combinatoires, et il est alors possible de formaliser les contraintes que doivent vérifier ces relations à l’aide de la notion d’orbite. Il existe plusieurs variantes de cette structure comme les arêtes ailées, les quad-edges, les DCEL…[Bau75, MP78, GS85, Män88, dBvKOS00] qui sont toutes très proches et peuvent être considérées comme des variantes du même principe original.
Les cartes combinatoires 2D ont été ensuite étendues en 3D [AK88, AK89, Lie88, Spe91] avant d’être définies de manière générique en nD [Lie89, Lie91, Lie94]. Elles permettent de représenter un complexe cellulaire orientable fermé, en décrivant les cellules du complexe ainsi que les relations d’adjacence et d’incidence entre ces cellules. Nous parlons de n-carte pour une carte combinatoire de dimension n.
Les cartes combinatoires permettent de représenter les quasi-variétés orientables fermées13. La notion de quasi-variété est introduite ici, comme une sous classe des pseudo-variétés [Elt94].
Cette notion est différente de la notion de variété topologique de dimension n classique [Ago76, Tak91] pour laquelle chaque point doit avoir un voisinage homéomorphe à une boule ouverte de dimension n (ou à une demi-boule ouverte si la variété topologique est à bord). De ce fait, une quasi-variété n’est pas forcément une variété [Lie93], excepté en dimension 2 (cf. exemple Fig. 2.11).
[a][b]
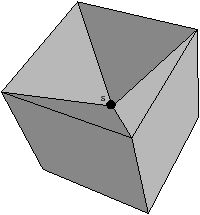
Figure 2.11: Exemple de quasi-variété qui n’est pas une variété. (b) Ce complexe cellulaire 3D est une quasi-variété car il est obtenu en collant les quatre pyramides de (a) le long de leurs faces (2-cellules). Par contre ce n’est pas une variété car le voisinage du point s n’est pas homéomorphe à la demi-boule ouverte h(B1/2)3 (c’est la demi boule qui est considérée car s est un point du bord).
Cette notion est incluse dans la notion de pseudo-variété présentée Section 2.1, mais n’est pas égale. En effet, dans la notion de quasi-variété, l’adjacence entre deux cellules de dimension n est nécessairement réalisée par une (n−1)-cellule, ce qui n’est pas le cas pour les pseudo-variétés. L’exemple de pseudo-variété donné Fig. 2.3 n’est pas une quasi-variété car il n’est possible à obtenir en collant des 2-cellules le long de 1-cellules.
Une n-carte peut s’obtenir de manière intuitive par décompositions successives des cellules d’un objet donné, comme présenté Fig. 2.12 pour un objet 2D.
[a][b]
[c]
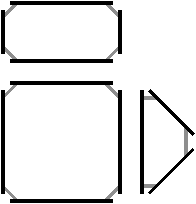
Figure 2.12: La décomposition d’un objet pour obtenir la carte combinatoire correspondante. (a) Un objet 2D (la face infinie n’est pas représentée). (b) Les faces de cet objet (sans la face infinie). (c) Les arêtes de ces faces.
À partir de l’objet à représenter Fig. 2.2.3, qui doit être fermé et orientable, nous commençons par distinguer les faces de cet objet Fig. 2.2.3, en conservant les relations d’adjacence entre chaque couple de faces (représentées par les traits noirs). Puis nous distinguons les arêtes de ces faces Fig. 2.2.3, en conservant les relations d’adjacence entre chaque couple d’arêtes (représentées par les traits gris).
L’objet initial a été décomposé en un ensemble d’éléments, les brins, qui constituent les briques de base de la définition des cartes combinatoires. Il faut ensuite reporter les différentes relations d’adjacence sur ces éléments. La relation d’adjacence entre les arêtes est représentée par une permutation, qui pour chaque brin donne le brin suivant de la même face (en respectant une orientation donnée). Cette relation est notée β1, car elle met en relation des arêtes qui sont des cellules de dimension 1. La relation d’adjacence des faces est représentée par une involution, β2, étant donné qu’elle met en relation des cellules de dimension 2 (par rapport aux notations 2D de la section précédente, β1 correspond à ϕ et β2 à α, l’intérêt de la notation βi étant sa généralisation en dimension quelconque).
Nous pouvons voir Fig. 2.2.3 la carte combinatoire de l’objet présenté Fig. 2.2.3 ainsi que la convention graphique généralement utilisée dans les schémas de cartes combinatoires.
[a][b]
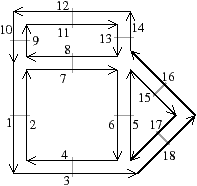
Figure 2.13: Exemple de carte combinatoire 2D et convention graphique. (a) Un objet 2D. (b) La carte combinatoire correspondante. Un brin est représenté par une flèche noire, éventuellement numéroté lorsque nécessaire. Deux brins en relation par β1 sont dessinés de manière consécutive (par exemple β1(1)=3). Deux brins en relation par β2 sont dessinés parallèles, proches et inversés, avec un petit segment perpendiculaire reliant les deux brins (par exemple β2(1)=2).
Cette méthode de décomposition d’un objet peut s’utiliser pour n’importe quelle dimension. Nous pouvons voir un second exemple de construction d’une carte combinatoire à partir d’un objet Fig. 2.14, mais cette fois pour la dimension 3.
[a][b]
[c]
[d]
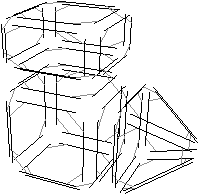
Figure 2.14: La décomposition d’un objet 3D pour obtenir la carte combinatoire correspondante. (a) Un objet 3D. (b) Les volumes de cet objet. (c) Les faces de ces volumes. (d) Les arêtes de ces faces.
L’objet présenté Fig. 2.2.3 est décomposé successivement pour distinguer ses volumes Fig. 2.2.3, puis les faces de ces volumes Fig. 2.2.3 et enfin les arêtes de ces faces Fig. 2.2.3. Les éléments obtenus sont les brins de la carte combinatoire représentant l’objet initial. Il faut maintenant reporter les relations d’adjacence entre chaque cellule sur les brins. Il existe, comme pour la dimension 2, une permutation β1 qui met en relation un brin et le brin suivant de la même face, et une involution β2 qui met en relation deux brins de deux faces adjacentes d’un même volume. Une involution supplémentaire β3 met en relation deux volumes adjacents. La carte combinatoire obtenue est représentée Fig. 2.2.3.
[a][b]
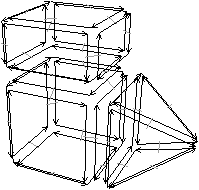
Figure 2.15: Exemple de carte combinatoire 3D et convention graphique (représentation partielle, le volume infini n’est pas dessiné). (a) Un objet 3D. (b) La carte combinatoire correspondante. La convention graphique utilisée est la même qu’en 2D. Généralement l’involution β3 n’est pas représentée car elle peut se retrouver sans ambiguïté par la forme des faces.
Cette méthode de construction permet d’appréhender les cartes combinatoires de manière intuitive. La Def. 17 donne la définition formelle des cartes combinatoires nD ce qui nous permettra par la suite d’utiliser ses propriétés algébriques. Nous trouvons cette définition par exemple dans [Lie94].
Les brins sont ici une notion abstraite, et servent uniquement de support pour les différentes applications. Seul β1 est une permutation, les autres βi sont des involutions. La dernière ligne de cette définition pose des contraintes sur la manière dont les brins sont mis en relation pour garantir que les objets représentés sont des quasi-variétés (cette contrainte ne s’applique pas pour n<3). Par exemple, en 3D, la contrainte ajoutée est que β1∘β3 doit être une involution, ce qui revient à dire que lorsque nous mettons deux brins de deux faces différentes en relation pour β3, nous devons obligatoirement mettre tous les autres brins de ces deux faces en relation deux à deux par β3.
Nous ajoutons dans cette définition la contrainte sur βi qui doit être sans point fixe, ∀ i: 2 ≤ i ≤ n qui n’est pas présente dans [Lie94], ceci pour éviter des configurations particulières, mais ausi pour être homogène avec la définition des G-cartes (présentée section suivante).
En effet, un brin b tel que βi(b)=b, pour un i: 2 ≤ i ≤ n correspond à replier une arête sur elle même. Nous obtenons alors une configuration où une arête n’a qu’un seul sommet dans son bord. Il est alors très difficile dans ce cas de faire un lien avec une représentation cellulaire
La deuxième raison concerne le lien avec les G-cartes. En effet, pour une G-carte, un brin b point fixe pour αi est un brin considéré sans successeur (et non comme son propre successeur). Ce cas est possible pour les G-cartes car elles peuvent représenter des objets ouverts, mais n’est pas possible ici car les cartes considérées doivent être fermées.
Interdire les points fixes évite les configurations particulières, et évite le problème de différentes interprétations pour les cartes et les G-cartes. Par contre, nous conservons la possibilité pour β1 de comporter des points fixes car un brin b tel que β1(b)=b correspond au cas des boucles (c-à-d une arête incidente deux fois au même sommet) qui n’est pas une configuration particulière (dans ce type de cas, l’arête a deux sommets dans son bord même si c’est deux fois le même).
Les motivations de [Lie94] pour autoriser les points fixes pour βi étaient de pouvoir convertir n’importe quelle G-carte orientable en carte combinatoire (cf. Section 2.2.4). Nous pensons que l’ajout de contraintes sur les βi qui doivent être sans point fixe rend les choses plus simples pour les cartes combinatoires et plus homogènes, mais cela a pour inconvénient de nous obliger à restreindre légèrement la convertion de G-carte en carte.
Revenons à la définition des cartes combinatoires. Comme les cartes sont fermées, nous allons avoir, de manière similaire à la dimension 2, la présence d’une n-cellule infinie par composante connexe de la carte qui «entoure» complètement la composante et permet de représenter une quasi-variété fermée. Nous notons β0 la permutation β1−1 , et βij la composition βj∘βi. Lorsque deux brins b1 et b2 sont tels que βi(b1)=b2, nous disons que b1 est i-cousu à b2. Étant donné que les βi, pour i ≠ 1, sont des involutions, si b1 est i-cousu à b2 alors b2 est i-cousu à b1. Remarquons que chaque brin possède forcément une image pour chaque βi, étant donné que ces βi sont des bijections. L’opération consistant à mettre en relation deux brins pour βi est appelée i-couture.
Une carte combinatoire est orientée. Le choix de l’orientation est une convention qu’il faut définir, puis conserver afin que toutes les opérations soient homogènes. La carte combinatoire d’orientation inverse (cf. Def. 18) est obtenue simplement en remplaçant β1 par son inverse β0. Par exemple, la carte de la Fig. 2.2.3 est l’inverse de la carte de la Fig. 2.2.3. Il est immédiat de prouver que l’inverse d’une carte combinatoire est une carte combinatoire, ainsi que de prouver que l’inverse de l’inverse d’une carte est la carte initiale.
Une carte combinatoire ne représente pas les cellules de manière explicite, mais de manière implicite comme des ensembles de brins obtenus à l’aide de la notion d’orbite. Chaque i-cellule est une orbite particulière (cf. Def. 19). Pour simplifier les écritures, nous notons ⟨h(βi1,…,βik)⟩ pour l’orbite contenant toutes les permutations possibles sauf celles-là, c-à-d ⟨{β1,…,βn}∖{βi1,…,βik}⟩. Nous utilisons également la notation ensembliste ⟨h(I)⟩, avec I={βi1,…,βik} pour l’orbite ⟨h(βi1,…,βik)⟩. Enfin, pour simplifier les notations des orbites, nous employons indifféremment ⟨{βi1,…,βik}⟩ ou ⟨βi1,…,βik⟩ car cela n’entraîne aucune ambiguïté.
Il y a deux cas différents. L’un pour la définition des 0-cellules (les sommets), et l’autre pour les autres cellules. Cela provient du fait que β1 est une permutation alors que les autres βi sont des involutions : les cartes combinatoires n’ont pas une définition homogène (ce problème est résolu dans la définition des cartes généralisées que nous présentons Section 2.2.4).
Une i-cellule incidente à un brin b peut se voir comme l’ensemble des brins que nous pouvons atteindre par un parcours d’origine b, en utilisant les β donnés dans l’orbite ainsi que leurs inverses. Dit autrement, c’est l’ensemble des brins b′ tel qu’il existe un chemin entre b et b′ utilisant uniquement les β donnés ainsi que leurs inverses. Les 0-cellules sont définies ainsi, car nous parcourons uniquement un brin sur deux, afin de n’atteindre que les brins «sortants» du sommet incident à b. Les autres i-cellules sont simplement l’orbite composée de tous les β sauf βi. En effet, comme βi permet de changer de i-cellule, en l’enlevant de l’orbite nous restons au cours du parcours sur les brins de la même i-cellule. Remarquons enfin que chaque ensemble de i-cellules est une partition de l’ensemble des brins de la carte. Chaque brin appartient donc exactement à chaque i-cellule, ∀ i∈{0,…,n}.
Sur l’exemple de la Fig. 2.2.3, le sommet incident au brin 7 est l’ensemble des brins de l’orbite ⟨β02⟩(7)= {5,7,13,16}. L’arête incidente au brin 7 est l’ensemble des brins de l’orbite ⟨β2⟩(7)= {7,8} (dans une carte combinatoire 2D, une arête est toujours composée de deux brins, ce n’est plus vrai en dimension supérieure). Enfin, la face incidente au brin 7 est l’ensemble des brins de l’orbite ⟨β1⟩(7)= {2,4,6,7}.
C’est la définition des 0-cellules qui rend nécessaire la condition dans la définition des cartes combinatoires que les βi, pour i>1, doivent être sans point fixe. En effet, si un brin b est tel que βi(b)=b, alors β0i−1(b)=βi1=β1(b) : le brin β1(b) appartient à la même orbite sommet que celle du brin b. Cela pose problème, car le fait d’enlever un brin d’une carte va avoir pour effet de bord de fusionner des orbites sommets, alors que cette modification simple n’est pas censée modifier les sommets (ce problème est résolu Section 2.2.5 avec l’introduction des cartes ouvertes).
Avec cette définition des i-cellules, la notion d’incidence se définit simplement en étudiant l’intersection des ensembles de brins des deux cellules (cf. Def. 20).
La Def. 21 définit alors la notion d’adjacence entre deux cellules en utilisant la notion d’incidence.
Pour n’importe quel brin b, βi(b) permet de changer de i-cellule (∀ i: 1≤ i≤ n), c’est-à-dire d’obtenir un brin b′ appartenant à la i-cellule adjacente à la i-cellule contenant b le long de la (i−1)-cellule contenant b15, mais change également de 0-cellule (pour i=1, car nous allons sur l’arête suivante de la même face, et pour i, 2≤ i≤ n, car deux brins en relation par βi sont d’orientations opposées). Comme dans le cas précédent cette seconde 0-cellule peut-être égale à la première dans le cas des boucles, c-à-d une arête incidente deux fois au même sommet.
Sur l’exemple de la Fig. 2.2.3, la 1-cellule c1(7)={7,8} est incidente à la 2-cellule c2(2)={2,4,6,7}, et la 2-cellule c2(9)={8,9,11,13} est adjacente à c2(2) car elles sont toutes deux incidentes à la 1-cellule c1(7). À partir du brin 8 incident à c0(8)={2,8,10} et c2(8)={8,9,11,13}, en effectuant β2(8) nous obtenons le brin 7 incident à c0(7)={5,7,13,16} et c2(7)={2,4,6,7} : nous avons changé de 0-cellule et de 2-cellule.
La notion de chemin entre deux brins se définit simplement comme une suite de brins en liaison deux à deux par des β (cf. Def. 22). Sur l’exemple de la Fig. 2.2.3, la séquence (1,2,4,6,5,15) est un chemin obtenu à partir du brin 1 et utilisant successivement β2, β1, β1, β2, β0.
Cette notion de chemin peut servir, comme en théorie des graphes, à définir la notion de connexité (cf. Def. 23).
La Def. 24 donne une seconde définition de la connexité, équivalente à la précédente, mais qui utilise la notion d’orbite au lieu de la notion de chemin.
Il suffit de tester la propriété pour un brin b ∈ B. En effet, si pour ce brin ⟨β1,…,βn⟩(b) =B, alors tous les brins de B appartiennent à cette orbite et la propriété est donc vraie pour chaque brin de B. Par contre si la propriété n’est pas vraie pour ce brin, alors il existe au moins un brin n’appartenant pas à la même orbite que b et donc quel que soit le brin considéré, son orbite ne contiendra jamais tous les brins.
La Def. 25 définit la notion de cartes isomorphes. Intuitivement deux cartes sont isomorphes s’il existe une bijection entre leur brins respectant les relations d’adjacence.
| ∀ i ∈ {1,…,n}, ∀ b ∈ B, f(βi(b))=βi′(f(b)) |
Un automorphisme est un isomorphisme entre une carte et elle même.
Lorsque nous considérons une subdivision d’un espace de dimension n, considérer l’espace dual revient à inverser les dimensions de l’espace de 0 à n en n à 0. De ce fait, une i-cellule dans l’espace initial va devenir une (n−i)-cellule dans l’espace dual. Cette transformation conserve les relations d’incidence et d’adjacence données dans les Def. 20 et Def. 21. Nous pouvons définir la carte combinatoire duale d’une carte donnée en gardant les mêmes brins, et en inversant l’ordre des permutations pour refléter ces changements de dimension. De plus, il faut composer les permutations βn−1, …, β1 avec βn pour obtenir une permutation (βn(n−1)) et des involutions (βni pour 1≤ i <n−1). Enfin, pour garantir que les βi, pour 2≤ i≤ n, sont sans point fixe, nous devons ajouter la contrainte que βn∘βi soit sans point fixe (ce qui revient à éviter un brin b tel que βn(b)=βi(b), ce qui un cas très particulier non utilisé dans les cas pratiques).
Un exemple de carte duale est donnée en 2D dans la Fig. 2.17. La 2-carte est C=(B,β1,β2) et sa carte duale C=(B,β21,β2). La Prop. 1 prouve la validité de la Def. 26 en montrant que la duale d’une carte combinatoire est une carte combinatoire.
[a][b]
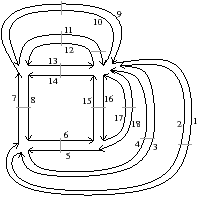
Figure 2.17: Exemple de cartes combinatoires duales. (a) Une 2-carte C=(B,β1,β2), composée de 7 sommets, 9 arêtes, et 4 faces. (b) La carte duale de C, C=(B,β1′,β2′)=(B,β21,β2), composée de 4 sommets, 9 arêtes, et 7 faces. Par exemple, β1′(6)=β21(6)=15.
Nous prouvons ici les deux propriétés principales liées à la définition des cartes duales : (1) la duale d’une carte est une carte ; (2) une i-cellule incidente à b d’une carte correspond à la (n−i)-cellule incidente à b dans la carte duale. Nous devons re-prouver ces propriétés déjà évoquées dans [Lie94] à cause de la contrainte supplémentaire que nous avons ajoutée.
Proof. Pour n=1, la preuve est immédiate car C=(B,β1), donc C=(B,β1−1) est une carte combinatoire.
Pour n>1. Tout d’abord, chaque βni, pour 1≤ i≤ n−2 est bien une involution par définition des cartes. βn est également une involution (car n ≥ 2), et βn(n−1) une permutation. Le fait que les involutions sont sans point fixe se déduit directement des préconditions sur les βn∘βi qui sont sans point fixe. Les 3 premières conditions de la Def. 17 sont donc vérifiées. En notant C=(B,β1′,…,βn′), la dernière condition de la définition des cartes combinatoires s’écrit ∀ i,j: 1 ≤ i<i+2≤ j ≤ n, βi′∘βj′ est une involution.
En re-écrivant les β′ en fonction des β, cette condition se re-écrit en βn(n−i)∘βn est une involution ∀ i: 1 ≤ i ≤ n−2, et βn(n−i)∘βn(n−j) est une involution ∀ i,j: 1 ≤ i <i+2≤ j≤ n.
Commençons par la première écriture : β(n−i)∘βn∘βn=β(n−i) (car βn est une involution). Comme 1 ≤ i ≤ n−2, alors 2≤ n−i ≤ n−1, donc βn−i est une involution par définition de C et donc βn(n−i)∘βn est une involution.
Pour la seconde écriture, nous étudions βn(n−j)n(n−i), pour 1 ≤ i < i+2 ≤ j ≤ n. Comme 2<j, βn(n−j) est une involution donc égale à son inverse β(n−j)n. Donc βn(n−j)n(n−i)=β(n−j)nn(n−i)= β(n−j)(n−i). Comme i < i+2 ≤ j, β(n−j)(n−i) est une involution et donc βn(n−j)n(n−i) aussi.
La propriété principale de la dualité, énoncée dans la Prop. 2, est que toute i-cellule d’une carte devient une (n−1)-cellule dans la carte duale. Grâce à cette propriété, nous pouvons directement déduire que les relations d’incidence et d’adjacence sont identiques dans une carte et dans sa carte duale.
Proof. Par définition de la carte duale, nous avons C=(B,βn(n−1),…,βn1,βn).
Considérons tout d’abord le cas 1≤ i<n : par définition des cellules, nous avons ci(b)=⟨β1,…,βi−1,βi+1,…,βn⟩(b), et c′n−i(b)=⟨β1′,…,βn−i−1′,βn−i+1′,…,βn′⟩(b). En re-écrivant les β′, nous obtenons c′n−i(b)=⟨βn(n−1),…,βn(i+1),βn(i−1),…,βn1,βn⟩. Lorsqu’une orbite contient une fonction f∘ g et la fonction f, alors par propriété des orbites, cette orbite est équivalente à la même orbite dans laquelle nous remplaçons f∘ g par g. En effet, dans les deux cas, comme nous effectuons toutes les compositions des fonctions de l’orbite et de leurs inverses, nous obtenons le même résultat. En utilisant ce principe, c′n−i(b) peut se re-écrire en ⟨βn−1,…,βi+1,βi−1,…,β1,βn⟩, qui est donc égal à ci(b) (car l’ordre des permutations dans une orbite n’importe pas).
Considérons maintenant le cas i=0. c0(b)=⟨β02,…,β0n⟩(b), et c′n(b)=⟨β1′,…,βn−1′⟩(b). En re-écrivant les β′, nous obtenons c′n(b)=⟨βn(n−1),…, βn1⟩(b). Si n=2, alors la preuve est directe car c0(b)=⟨β02⟩, et c′2(b)=⟨β1′⟩=⟨β21⟩=⟨β02⟩. Si n>2, En utilisant la même règle que précédemment, l’orbite est identique à la même orbite dans laquelle nous composons tout les éléments sauf le dernier avec βn1. Nous obtenons l’orbite ⟨βn1n(n−1),…,βn1n2,βn1⟩(b). Comme n>2, alors βn1 est une involution donc égal à son inverse β0n. Nous pouvons donc re-écrire l’orbite en ⟨β0nn(n−1),…,β0nn2,βn1⟩(b), et donc en ⟨β0(n−1),…,β02,β0 n⟩(b), ce qui prouve que c0(b)=c′n(b).
Reste le cas i=n. cn(b)=⟨β1,…,βn−1⟩(b), et c′0(b)=⟨β02′,…,β0n′⟩(b). En re-écrivant les β′, nous obtenons c′0(b)=⟨β(n−1)nn(n−2),…,β(n−1)nn1,β(n−1)nn⟩, donc en simplifiant les βnn, nous obtenons directement ⟨β(n−1)(n−2),…,β(n−1)1,β(n−1)⟩. En combinant chaque membre sauf le dernier avec β(n−1), nous obtenons ⟨β(n−2),…,β1,β(n−1)⟩ ce qui prouve que cn(b)=c′0(b).
Nous pouvons vérifier cette propriété sur l’exemple précédent en vérifiant que chaque i-cellule de la carte de la Fig. 2.2.3 se transforme bien en une (2−i)-cellule dans la carte de la Fig. 2.2.3. Par exemple le sommet c0(10)={2,8,10} se transforme bien dans la face c′2(10) dans la carte duale, l’arête c1(10)={9,10} se transforme bien dans l’arête c′1(10) dans la carte duale, et la face c2(8)={8,9,11,13} se transforme bien dans le sommet c′0(8) dans la carte duale.
Les cartes généralisées sont une extension des cartes combinatoires permettant de représenter les quasi-variétés orientables ou non avec ou sans bord [Lie89, Lie91, Lie94]. Leur principal avantage est que leur définition est homogène à toutes les dimensions, contrairement aux cartes combinatoires, ce qui simplifie les définitions et l’écriture des algorithmes. De plus, cette homogénéité fait que la définition des cartes généralisées est directement valide pour les brins avec ou sans point fixe, car nous n’avons plus le problème qui se posait dans les cartes combinatoires lors de la définition des sommets. Ces cartes généralisées sont proches de la structure de cell-tuple [Bri89, Bri93].
Pour définir une carte généralisée de manière intuitive, nous appliquons le même principe de décomposition que celui utilisé pour les cartes combinatoires, mais nous effectuons une décomposition supplémentaire afin de distinguer les sommets. Si nous reprenons le premier exemple utilisé pour les cartes combinatoires présenté Fig. 2.12, nous avons obtenu au final la décomposition rappelée Fig. 2.2.4.
[a][b]
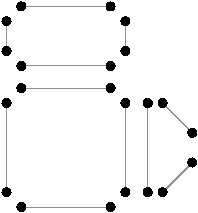
Figure 2.18: La décomposition supplémentaire d’un objet 2D pour obtenir une carte généralisée. (a) Les arêtes obtenues Fig. 2.12 après décompositions successives. (b) Les sommets de ces arêtes.
Nous décomposons ensuite les sommets, à partir de cette décomposition en arêtes et obtenons la décomposition présentée Fig. 2.2.4, où les relations d’adjacence entre les sommets d’une arête sont représentées par les segments gris. Les éléments obtenus sont les brins de la carte généralisée. Il suffit ensuite, comme pour les cartes combinatoires, de reporter les relations d’adjacence sur ces brins pour obtenir la carte généralisée présentée Fig. 2.2.4.
[a][b]
[c]
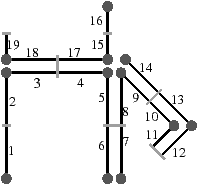
Figure 2.19: Exemple de carte généralisée 2D et convention graphique. (a) La carte combinatoire de la Fig. 2.13. (b) La carte généralisée représentant le même objet. Un brin est représenté par un segment avec un disque à une extrémité et un petit segment perpendiculaire à l’autre extrémité. Deux brins reliés par α0 sont dessinés de manière consécutive, alignés, et partagent le même petit segment perpendiculaire (par exemple α0(1)=2). Deux brins reliés par α1 partagent le même disque (par exemple α1(1)=6). Deux brins reliés par α2 sont dessinés de manière parallèle et partagent le même petit segment perpendiculaire (par exemple α2(1)=4). (c) Une 2G-carte ouverte (0-ouverte, 1-ouverte et 2-ouverte). Les brins 11, 12 et 19 sont 0-libres, les brins 1, 6, 7, 14 et 16 sont 1-libres et les brins 1, 2, 15, 16 et 19 sont 2-libres.
Étant donné que nous avons également séparé les sommets pour les cartes généralisées, nous n’avons plus besoin, comme pour les cartes combinatoires, d’utiliser une permutation pour parcourir les faces. En effet, chaque «côté» d’une arête sera lié avec l’arête suivante de la face pour ce sommet. Il existe donc une involution α0 qui met en relation les deux brins de la même face et de la même arête, une involution α1 qui met en relation les deux brins de la même face et du même sommet, et une involution α2 qui met en relation les deux brins de la même arête et du même sommet.
Comme pour les cartes combinatoires, nous ne représentons pas de manière explicite toutes les involutions et utilisons la représentation intuitive présentée Fig. 2.2.4. Deux brins cousus par α0 sont représentés par un seul segment portant un petit segment perpendiculaire en son milieu, deux brins cousus par α1 sont représentés de manière contiguë séparés par un disque, et deux brins cousus par α2 sont représentés parallèles et proches, avec la barre représentant α0 traversant les deux segments.
Nous pouvons voir Fig. 2.20 le même principe appliqué en dimension 3 à notre exemple de la Fig. 2.14. Pour les cartes combinatoires, nous avons obtenu au final la décomposition en arêtes rappelée Fig. 2.2.4.
[a][b]
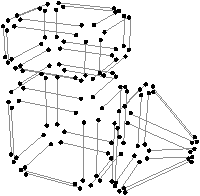
Figure 2.20: La décomposition supplémentaire d’un objet 3D pour obtenir la carte généralisée correspondante. (a) Les arêtes obtenues Fig. 2.14 après décompositions successives. (b) Les sommets de ces arêtes.
La décomposition en sommets des arêtes de cette figure est présentée Fig. 2.2.4, et la carte généralisée correspondante Fig. 2.2.4.
[a][b]
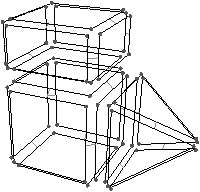
Figure 2.21: Exemple de carte généralisée 3D et convention graphique. (a) La carte combinatoire de la Fig. 2.15. (b) La carte généralisée représentant le même objet. La convention graphique utilisée est la même qu’en 2D. Généralement α3 n’est pas représenté car il peut se retrouver sans ambiguïté par la forme des faces.
La Def. 27 [Lie91] donne la définition des cartes généralisées en dimension n :
En comparaison avec les cartes combinatoires, il existe une involution supplémentaire, et il n’y a plus de différence entre les α qui sont tous des involutions. De plus, ces involutions peuvent maintenant toutes être avec ou sans point fixe sans que cela change la définition ni que cela pose de problème pour la définition des cellules. Les nG-cartes sont définies à partir de n=−1, afin de pouvoir définir la G-carte vide, composée uniquement d’un ensemble de brins sans aucune involution. Nous parlons de brin i-libre pour un brin b point fixe pour αi (c-à-d tel que αi(b)=b). C’est un brin n’ayant pas d’autre brin en relation par αi, et qui est alors considéré comme n’ayant pas de successeur pour αi et non pas comme étant son propre successeur. De manière similaire à la notation βij, nous notons αij=αj ∘ αj.
Nous disons qu’une G-carte est i-fermée si aucun de ses brins n’est i-libre. Une carte n’étant pas i-fermée est dite i-ouverte. Enfin, nous parlons de G-carte fermée pour une G-carte i-fermée pour toutes les dimensions de l’espace, et de G-carte ouverte sinon (par exemple la 2G-carte de la Fig. 2.2.4 est fermée, et celle de la Fig. 2.2.4 est ouverte).
Les G-cartes sont totalement homogènes, ce qui simplifie les définitions et les algorithmes comme nous pouvons le voir, par exemple, pour la Def. 28 des cellules. Comme pour les cartes combinatoires, nous utilisons la notation ⟨h(αi1,…,αik)⟩ pour l’orbite contenant toutes les involutions possibles sauf celles-là, c-à-d ⟨{α0,…,αn}∖{αi1,…,αik}⟩, ainsi que la notation ensembliste ⟨h(I)⟩, avec I={αi1,…,αik}, pour l’orbite ⟨h(αi1,…,αik)⟩.
Cette définition de cellule est maintenant homogène pour toutes les dimensions i∈{0,…,n} : il n’est plus nécessaire de distinguer les sommets des autres cellules. De ce fait, le cas des points fixes ne pose plus de problème car la définition des cellules n’utilise jamais la composition de deux involutions, ce qui était la raison du problème pour la définition des sommets comme nous l’avons vu dans la section précédente.
Les définitions d’incidence et d’adjacence données pour les cartes combinatoires (Defs. 20 et 21) sont toujours valides pour les G-cartes car elles se basent sur la notion de cellule, notion que nous venons de redéfinir pour les G-cartes. Les Defs. 22 et 25 de chemin et d’isomorphisme sont identiques pour les G-cartes, sous réserve de remplacer βi par αi, la Def. 23 de connexité est toujours valide car elle utilise la notion de chemin, tandis que pour la seconde définition de connexité (Def. 24), il faut remplacer l’orbite utilisée par ⟨α0,…,αn⟩(b)=B.
Mais pour représenter des quasi-variétés orientables, les G-cartes sont deux fois plus coûteuses en espace mémoire que les cartes combinatoires. Ce surcoût en mémoire peut être prohibitif, et c’est pour cette raison que selon les applications, nous utilisons les cartes combinatoires ou les cartes généralisées, pour privilégier la généricité des opérations ou l’espace mémoire.
En effet, lorsque nous travaillons avec des G-cartes orientables, les deux modèles sont équivalents : nous savons effectuer facilement la transformation permettant de passer aux cartes combinatoires, et lorsque nous travaillons avec une carte combinatoire, nous pouvons définir sans problème la carte généralisée correspondante. Afin de réaliser cette conversion, nous devons être en mesure de savoir si une G-carte est orientable ou non. C’est l’objet de la Def. 29 donnée initialement dans [Lie94], mais que nous modifions ici pour se restreindre aux nG-cartes sans point fixe pour αi∘α0, ∀ i: 2≤ i≤ n.
Nous ajoutons la contrainte sur l’absence de point fixe pour αi∘α0, ∀ i: 2≤ i≤ n, pour garantir que HG soit une carte combinatoire valide au sens de notre Def. 17, c’est à dire sans point fixe pour βi, ∀ i: 2≤ i≤ n. Cette contrainte n’était pas présente dans la définition de [Lie94] car l’auteur utilisait la définition étendue des cartes combinatoires ayant éventuellement des points fixes (il faut également noter que, dans ce même article, la définition à été étendue aux G-cartes pouvant avoir des points fixes pour αn). Cette restriction n’est pas limitante car elle interdit uniquement des configurations très particulières dans lesquelles un brin b est lié avec b′ à la fois par α0 et par un autre αi. De ce fait, nous avons une arête repliée auquel il est très difficile d’associer un sens dans le complexe cellulaire correspondant.
Cette définition permet facilement de tester, étant donné une G-carte, si elle est orientable ou non. De manière intuitive, une G-carte orientable contient les deux orientations possibles de la carte combinatoire correspondante (cf. l’exemple de la Fig. 2.2.4)). Cette définition est valable uniquement pour les G-cartes fermées connexes pour la même raison qui pose problème lors de la définition des sommets dans les cartes combinatoires ouvertes. En effet, nous composons ici deux involutions αi∘α0, ce qui va poser problème par exemple si α0 a un point fixe b car nous allons alors avoir α0i(b)=αi(b) (cf. l’exemple de la Fig. 2.2.4). Par contre, cette définition s’étend directement aux G-cartes fermées non connexes : une nG-carte fermée est orientable si chaque composante connexe est orientable.
[a][b]
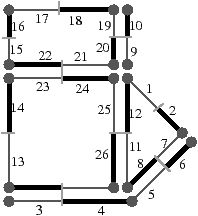
Figure 2.22: Orientation des cartes généralisées. (a) Une G-carte fermée orientable. Les brins en gras appartiennent à la même composante connexe de la n-carte HG=(B,α01,…,α0n). (b) Si la G-carte est ouverte, la n-carte HG à une seule composante connexe même lorsqu’elle est orientable. En effet, dès qu’un brin est i-libre pour n’importe quel i: 0≤ i ≤ n (par exemple le brin 1 qui est 2-libre), il existe un α0i qui va donner un brin de la seconde orientation de la G-carte (par exemple α02(1)=2 alors que les brins 1 et 2 appartiennent à deux orientations différentes de la G-carte).
La conversion entre une carte combinatoire et une carte généralisée peut s’effectuer sans contrainte, étant donné que le domaine de modélisation des cartes généralisées inclut celui des cartes combinatoires.
De manière informelle, pour convertir une carte en G-carte, nous «coupons» chaque brin bi de C en deux brins bi et ci. Nous pouvons voir Fig. 2.23 un exemple de conversion d’une carte en G-carte.
[a][b]
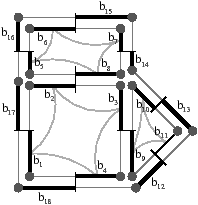
Figure 2.23: Un exemple de conversion de carte en G-carte. (a) Une carte combinatoire 2D. (b) La carte généralisée correspondante.
Chaque brin bi de la carte reste, dans la G-carte, le brin incident à la même face, à la même arête et au même sommet. Le brin de la même face, de la même arête et du sommet opposé est ci, qui est donc 0-cousu à bi. La définition des involutions de la G-carte se fait ensuite sans difficulté, en différenciant à chaque fois deux cas, suivant que le brin concerné est un brin de la carte, donc possédant des β coutures, ou un nouveau brin. De plus, il faut différencier la définition de α1 de la définition des autres α, du fait que les cartes ne sont pas homogènes.
La transformation inverse se fait de manière directe, étant donné que nous pouvons définir chaque β comme une composition de certains α. Mais pour cela, il faut nécessairement que la G-carte soit orientable. En effet, si elle ne l’est pas, il n’existe pas de carte représentant la même subdivision de l’espace. De plus, cette transformation est, comme la définition de G-carte orientable, valable uniquement pour les G-cartes connexes, fermées, et telles que ∀ i: 2≤ i≤ n, αi∘α0 soit sans point fixe. La carte combinatoire obtenue correspond à une composante connexe de la carte des orientations, c’est à dire à une orientation de la G-carte.
La carte C est définie en conservant un brin sur deux de la G-carte. En effet, comme nous savons que la G-carte est orientable et fermée, l’orbite ⟨α01,…,α0n⟩(b) va contenir un brin sur deux de la G-carte, ce qui n’est pas le cas sinon. La définition des différentes applications β sur cet ensemble de brins se fait directement : chaque βi étant simplement la composition de αi avec α0. Remarquons que la carte ainsi définie représente une orientation de la G-carte. Il est possible de définir la carte représentant l’autre orientation possible, en prenant comme brin de départ pour la définition de B′, un brin n’appartenant pas à la première orientation. Il est facile de prouver que nous obtenons bien une carte combinatoire valide. Notre condition supplémentaire sur l’absence de point fixe pour βi, ∀ i: 2≤ i≤ n découle directement de la condition ∀ i: 2≤ i≤ n, αi∘α0 est sans point fixe.
Concernant la définition de la G-carte duale, nous retrouvons ici tout l’intérêt des cartes généralisées qui grâce à leur définition homogène permettent une définition plus simple que pour les cartes combinatoires :
De plus, les preuves que la duale d’une G-carte est une G-carte, et que la cellule ci(b) dans G est égale à la cellule c′(n−i)(b) dans la carte duale G′ sont directes de par la définition des G-cartes et des cellules.
Comme nous venons de le voir, les cartes combinatoires ne peuvent pas représenter des objets ouverts. Cette limitation est due à la définition des 0-cellules qui utilise la notion d’orbite pour les compositions β0i, ∀ i, 1<i ≤ n, ce qui pose problème pour les brins étant points fixes (de manière similaire au problème de définition de l’orientation d’une G-carte avec points fixes).
Afin de régler ces problèmes, les cartes combinatoires ouvertes ont été récemment définies [PABL07], permettant de représenter des subdivisions orientables avec ou sans bord. Le principe utilisé ici pour représenter les brins libres n’est pas le même que celui utilisé dans les G-cartes qui consiste à utiliser des points fixes. En effet, cela n’est pas possible pour β1 car un point fixe pour β1 représente une boucle (une arête cousue avec elle-même) et non un brin sans successeur. De ce fait, nous considérons un élément spécifique є, en plus des brins, et autorisons les brins à être mis en relation avec є pour indiquer qu’ils sont 1-libres. Nous conservons ce même principe pour les autres βi dans le but d’avoir des définitions homogènes.
De par cette définition des brins libres, la contrainte sur les βi, pour i ≠ 1, qui doivent être sans point fixe, est conservée, comme dans la Def. 17 des cartes combinatoires, et pour les mêmes raisons.
Lorsque des brins sont i-cousus avec є, βi n’est plus une permutation ou une involution sur B, mais ce que nous appelons une permutation partielle ou involution partielle car seuls les brins d’un sous-ensemble X⊆ B sont liés à des brins de B, les brins de B ∖ X étant liés à є. La définition d’une permutation partielle et de son inverse est donnée Def. 34.
Une permutation partielle f sur E peut être vue comme une bijection entre deux sous-ensembles1 F et G de E telle que les éléments de E qui n’appartiennent pas à F sont liés avec є par f, et les éléments de E qui n’appartiennent pas à G sont liés avec є par f−1. Si ∄ e ∈ E tel que f(e)=є, alors la permutation partielle f est une permutation définie sur E.
Nous montrons dans la Prop. 3 que l’inverse est «correctement défini» car l’inverse de l’inverse d’une permutation partielle est bien la permutation partielle initiale.
Proof. Nous notons g=f−1 (qui est bien une permutation partielle) et nous étudions g−1. Soit e ∈ E, il y a deux cas :
Une involution partielle (cf. Def. 35) est une permutation partielle qui vérifie, pour les brins non libres, la propriété d’une involution (c-à-d f(f(e))=e).
Comme une involution partielle est une permutation partielle, son inverse est définie. La Prop. 4 prouve qu’un involution partielle est égale à son inverse.
Proof. Soit e ∈ E. Il y a deux cas.
Nous pouvons également vérifier que la composition de deux permutations partielles vérifie les propriétés classiques de la composition:
Proof. Prouvons tout d’abord que (f ∘ g) est une permutation partielle. Soit e ∈ E. Il y a deux cas.
(1) Si g(e)=є ou f(g(e))=є, il n’y a pas de condition dans la définition d’une permutation partielle dans ce cas.
(2) Sinon, g(e)=e′≠ є et f(e′)=e″ ≠ є. Alors par Def. 34, ∄ x ≠ e, tel que g(x)=e′, et ∄ y ≠ e′, tel que f(y)=e″. Donc ∄ x ≠ e tel que (f ∘ g)(x)=e″ et donc (f ∘ g) est une permutation partielle.
Prouvons maintenant que (f ∘ g)−1 = g−1 ∘ f−1. Soit e ∈ E. Il y a deux cas selon que (f ∘ g)−1(e)=є ou non.
(1) Par définition des permutations partielles, (f ∘ g)−1(e)=є si ∄ e′ ∈ E tel que (f ∘ g)(e′)=e. Supposons maintenant que g−1 ∘ f−1(e)=e′ ≠ є. Alors il existe e″ ∈ E tel que f(e″)=e et g(e′)=e″. Dans ce cas, nous avons (f ∘ g)(e′)=e ce qui est en contradiction avec (f ∘ g)−1(e)=є. Donc (f ∘ g)−1(e)=g−1 ∘ f−1(e).
(2) Si (f ∘ g)−1(e)=e′ ≠ є. Alors par définition f ∘ g(e′)=e. Donc il existe e″ ∈ E tel que g(e′)=e″ et tel que f(e″)=e. De ce fait f−1(e)=e″ et g−1(e″)=e′. Donc (f ∘ g)−1(e)=g−1 ∘ f−1(e).
Les cartes combinatoires ouvertes peuvent maintenant être définies :
Les cartes ouvertes diffèrent des cartes sur trois points : (1) β1 est une permutation partielle et plus une permutation ; (2) les autres βi, 2 ≤ i ≤ n, sont des involutions partielles ; (3) la condition 4 est modifiée afin que βi∘βj soit une involution partielle, et cette condition doit également être testée pour β0∘βj. Un exemple de 2-carte ouverte est donné Fig. 2.24.
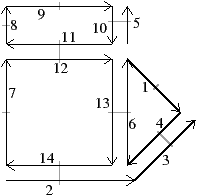
1 2 3 4 5 6 7 8 9 10 11 12 13 14 β1 4 3 є 6 є 1 12 9 10 11 8 13 14 7 β2 є 14 4 3 10 13 є є є 5 12 11 6 2
Figure 2.24: Exemple de 2-carte ouverte. Les brins 3 et 5 sont 1-libres, et les brins 1, 7, 8 et 9 sont 2-libres.
Les deux premières différences proviennent directement du fait de vouloir représenter des brins libres. La troisième différence provient du fait que si β1∘βj est une involution partielle, alors β0∘βj n’est pas nécessairement une involution partielle. En effet, considérons une 3-carte composée de 3 brins : b1, b2, b3, avec β1(b2)=b1 et β3(b1)=b3 (et donc β3(b3)=b1 pour que β3 soit une involution partielle), les autres β étant tous reliés à є. Alors, pour tout brin b, nous avons β1∘β3=є donc β1∘β3 est une involution partielle. Par contre β0∘β3 n’est pas une involution partielle car β0∘β3(b3)=b2 tandis que β0∘β3(b2)=є.
Nous étudions maintenant les propriétés des cartes combinatoires ouvertes. La Prop. 3 implique directement que β0−1=β1. La Prop. 6 traite des propriétés des compositions des permutations et involutions partielles.
Proof. βi∘βj est une involution partielle par Def. 36, donc égal à son inverse (βi∘βj)−1 (par Def. 35). Étudions les 3 cas :
Nous allons maintenant utiliser cette proposition pour prouver la Prop. 7 montrant que les βj∘βi sont également des involutions partielles.
Proof. La preuve est directe en utilisant le fait que ∀ i,j: 0 ≤ i<i+2≤ j ≤ n et j ≥ 3, βi∘βj est une involution partielle par la Def. 36, et en utilisant la Prop. 6.
Le fait que βi∘βj et βj∘βi soient des involutions partielles montre la validité de la définition des cartes ouvertes pour les brins non libres puisque, pour ces brins, nous nous ramenons à l’équivalent de la définition des cartes originales. Mais nous devons également étudier l’impact de cette condition sur les brins libres. C’est ce qui est fait dans la Prop. 8 où nous prouvons que tout couple de brins (b, βi(b)) a le même «type» de voisinage pour βj (c-à-d ils sont soit tous deux j-libres, soit j-cousus).
Proof. Pour la première proposition, si b est non i-libre, soit b′=βi(b). Supposons b est j-libre et b′ non. Alors notons βj(b′)=b″, et donc βij−1(b″)=b tandis que βij−1(b)=є car b est j-libre et βj−1=βj car j≥ 3. Contradiction avec le fait que βij−1 soit une involution, donc b′ est j-libre. De manière symétrique, supposons b non j-libre et b′ j-libre. Alors notons βj(b)=b″, et donc βji(b″)=b′ alors que βji(b′)=є car b′ est j-libre. Contradiction avec βji est une involution, donc b′ n’est pas j-libre.
Pour la seconde proposition, nous effectuons une démonstration similaire avec b et b′=βj(b). Comme nous savons que βij et βji sont des involutions, et en utilisant les Props. 4 et 5 (sur l’inverse d’une involution partielle et sur l’inverse de la composition de deux permutations partielles) nous pouvons à chaque fois conclure.
Comme pour les G-cartes, nous employons les termes de carte i-fermée, i-ouverte, fermée et ouverte selon la présence ou non de brin i-libre. Dans la suite de ce manuscrit, pour alléger les écritures, nous parlerons de carte combinatoire ou carte pour désigner des cartes pouvant être ouvertes ou non, et nous préciserons si la carte est fermée lorsqu’il sera nécessaire de faire la distinction.
Nous devons maintenant modifier la notion d’orbite pour enlever l’élément є des éléments de l’orbite. En effet, dans la définition originale, l’orbite d’un brin est l’ensemble des éléments atteignables par application des permutations et de leurs inverses. Cet ensemble peut donc désormais contenir є, ce qui n’est pas correct.
Cette notion d’orbite sert, comme pour les cartes combinatoires fermées, à définir les cellules. De ce fait, la Def. 19 des i-cellules dans les cartes fermées est toujours valide pour les cartes ouvertes, pour i>1. En effet, l’orbite permet bien de récupérer tout les brins de la cellule, tout en évitant є. Par contre, nous devons modifier la définition des sommets (Def. 38 des 0-cellules), car la définition originale est incomplète à cause de la présence éventuelle de brins libres.
Par rapport à la définition originale, nous ajoutons dans l’orbite considérée les βij avec 2 ≤ i < j ≤ n pour garantir de ne pas rater de brins du fait de la présence de brins 0 ou 1-libres. Prenons l’exemple d’une 3-carte C={B,β1,β2,β3} composée de 3 brins numérotés 1,2 et 3, tel que β2(1)=2 et β3(2)=3 (et donc β2(2)=1 et β3(3)=2). Les brins 1 et 3 appartiennent au même sommet (le fait d’utiliser βi avec 2≤ i ≤ n fait changer de sommet, donc utiliser β2 puis β3 redonne le même sommet). Mais il n’existe pas de chemin allant du brin 1 au brin 3 en utilisant β02, β03 et leurs inverses β21 et β31. En effet, le brin 1 étant 0-libre, et les brins β2(1) et β3(2) étant 1-libres, la valeur de chacune de ces permutations pour le brin 1 est égale à є. Le fait d’ajouter β23 dans l’orbite sommet résout ce problème. Il faut noter que ce cas ne peut pas se produire pour les autres i-cellules, 0<i≤ n, car l’orbite n’utilise pas de composition de permutations.
Sur l’exemple de la Fig. 2.24, le sommet incident au brin 12 est {8,12}. L’arête incidente au brin 1 est <β2>(1) = {1} (car le brin 1 est 2-libre), tandis que l’arête incidente au brin 11 est <β2>(11) = {11,12}. La face incidente au brin 2 est <β1>(2) = {2,3}.
Les définitions de carte inverse, incidence, adjacence, chemin et carte connexe, données dans le cadre des cartes fermées, sont toujours valides dans le cadre des cartes ouvertes. La Def. 25 d’isomorphisme de cartes doit être modifiée uniquement pour ajouter la condition que f(є)=є.
La Def. 26 des cartes duales est toujours valide dans le cadre des cartes ouvertes, à condition que les cartes soient n-fermées. En effet, comme la définition de carte duale compose βn avec les autres β, si une carte est n-ouverte, cela peut avoir pour conséquence d’obtenir un résultat qui ne vérifie pas la condition 4 de la définition des cartes.
Prenons comme exemple une 3-carte C=(B,β1,β2,β3) composée de 3 brins numérotés 1, 2 et 3, et tel que β2(1)=2 et β3(1)=3 (donc β2(2)=1 et β3(3)=1), tous les autres β donnant є. Cette carte vérifie bien la condition 4 de la définition des cartes ouvertes (qui en 3D est que β13 est une involution partielle). La carte duale de cette carte est C=(B,β1′,β2′,β3′)=(B,β32,β31,β3). Nous avons donc β3′(1)=β3(1)=3, β1′(3)=β32(3)=2 et β3′(3)=β3(3)=1, tous les autres β donnant є. Ce n’est donc pas une carte combinatoire car β03′ n’est pas une involution partielle (car β03′(2)=1 et β03′(1)=є).
En ajoutant un brin 4 à la carte C tel que β3(2)=4 (et donc β3(4)=2) sans changer les β des autres brins, la carte C est maintenant 3-fermée. Pour la carte duale C=(B,β1′,β2′,β3′)=(B,β32,β31,β3), nous avons maintenant β1′(3)=2, β1′(4)=1, β3′(1)=3, β3′(2)=4, β3′(3)=1, et β3′(4)=2, tous les autres β étant liés à є. C est ici une 3-carte : β03′ est bien une involution partielle (β03′(1)=2 ; β03′(2)=1 ; β03′(3)=є et β03′(4)=є).
Les preuves faites par rapport aux cartes duales dans le cadre des cartes fermées sont similaires, mais elles doivent être légèrement modifiées car la composition d’une involution partielle avec elle-même n’est plus l’identité (c’est l’identité seulement pour les brins non libres), et cela est utilisé souvent dans les démonstrations. Mais résoudre ce problème se fait simplement en distinguant à chaque fois les cas des brins reliés à є des autres cas. C’est le cas pour la Prop. 1 disant que la duale d’une carte est une carte, et pour la Prop. 2 qui prouve qu’une i-cellule incidente à b dans une carte est égale à la (n−i)-cellule incidente à b dans la carte duale. Il faut noter que comme la carte est désormais ouverte, lorsqu’une i-cellule est ouverte (un de ses brins est libre pour un βj, j≠ i) dans la carte initiale, la (n−i)-cellule correspondante est également ouverte dans la carte duale.
Nous présentons un exemple de carte ouverte duale Fig. 2.25. Sur cet exemple, la 2-carte est ouverte mais 2-fermée. Nous pouvons voir par exemple que β1′(5)=β21(5)=7, tandis que β1′(1)=є car β21(1)=є. Nous pouvons également vérifier sur cet exemple que les i-cellules de la carte de la Fig. 2.2.5 se transforment bien en (2−i)-cellules dans la carte de la Fig. 2.2.5. Par exemple la 0-cellule c0(5)={5,7,9} de la carte initiale se transforme bien en la 2-cellule c′2(5) dans la carte duale ; la 1-cellule c1(5)={1,5} de la carte initiale se transforme bien en la 1-cellule c′1(5) dans la carte duale ; et la 2-cellule c2(8)={8,9,10} de la carte initiale se transforme bien en la 0-cellule c′0(8) dans la carte duale.
[a][b]
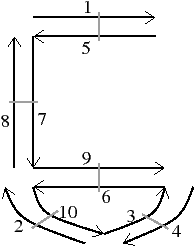
Figure 2.25: Exemple de duale d’une carte combinatoire ouverte. (a) Une 2-carte combinatoire ouverte, mais 2-fermée. (b) La 2-carte combinatoire duale.
Le problème évoqué ci-dessus de non-validité de la carte duale d’une carte n-ouverte ne se pose pas dans ces termes pour n≤ 2. En effet, pour ces cartes, la condition 4 ne s’applique pas, et donc n’importe quel ensemble de brins, avec n’importe quelles applications β, est une carte combinatoire valide en 0, 1 et 2D. Mais par contre, comme nous pouvons voir Fig. 2.26, le problème qui se pose alors est qu’il peut ne plus y avoir de correspondance entre les i-cellules de la carte et les (n−i)-cellules de la carte duale. Par exemple la face c2(8)={8,9,10,11} de la carte de la Fig. 2.2.5 est éclatée dans les deux sommets c′0(8)={8,10,11} et c′0(9)={9} dans la carte duale de la Fig. 2.2.5. De ce fait, la contrainte sur la carte qui doit être n-fermée est nécessaire pour tout n, y compris n≤ 2.
[a][b]
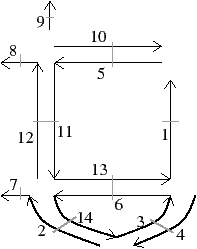
Figure 2.26: Exemple de problème pour la duale d’une carte combinatoire 2-ouverte. (a) Une 2-carte combinatoire 2-ouverte. (b) La 2-carte combinatoire duale correspondante. C’est une carte combinatoire valide, mais il n’y a pas correspondance entre les i-cellules de la première carte et les (n−i)-cellules de la carte duale (par exemple la face c2(8)={8,9,10,11} est éclatée dans les deux sommets c′0(8)={8,10,11} et c′0(9)={9}.
Comme nous venons d’introduire les cartes combinatoires ouvertes, nous pouvons maintenant re-considérer le problème de conversion entre carte et G-carte. En effet, la définition initiale imposait que la G-carte soit fermée afin que la carte combinatoire le soit également. Mais cette contrainte n’est désormais plus nécessaire. Mais pour supprimer cette contrainte, nous devons au préalable étendre la Def. 29 permettant de tester si une G-carte est orientable aux G-carte ouvertes, car cette définition est utilisée dans la définition de la conversion.
Pour cela, nous devons considérer différemment les brins points fixes de la G-carte des autres brins. Pour cela, nous définissons la conversion d’une involution en involution partielle sans point fixe, qui va transformer la convention utilisée pour les brins libres dans les G-cartes (c-à-d les brins points fixes) en la convention utilisée pour les brins libres dans les cartes ouvertes (c-à-d les brins liés à є).
Il est facile de prouver que si f est une involution sur E, alors f• est une involution partielle. Nous pouvons également remarquer que l’involution partielle f• est sans point fixe car tous les points fixes de f ont été transformés en éléments en relation avec є. Nous pouvons maintenant utiliser cette transformation pour re-définir la notion de G-carte orientable dans la Def. 40.
L’utilisation de la composition avec point fixe nous permet d’avoir la même définition que dans le cas des G-cartes fermées, après avoir transformé les involutions en involutions partielles. Cette définition semble montrer que si les cartes généralisées étaient définies de manière similaire aux cartes combinatoires ouvertes, avec des involutions partielles et є pour les points fixes, certaines définitions pourraient être plus simples. Il pourrait être intéressant d’étudier plus précisément cette possibilité en comparant les deux approches de manière approfondie.
La contrainte sur la nG-carte qui doit être 0-fermée est nécessaire afin de s’assurer que pour toute G-carte connexe, HG soit bien composée de deux composante connexes. En effet, sans cette contrainte, la G-carte peut-être composée de plusieurs parties reliées par des brins 0-libres. Dans ce cas, il ne sera pas possible de «passer» à travers ces brins car tous les αi•∘α0 vont donner є. De ce fait, le nombre de composantes connexes de HG ne serait plus lié à l’orientabilité de G. Prenons par exemple la 2G-carte G=(B,α0,α1,α2) composée de trois brins numérotés 1, 2 et 3, et tel que α2(1)=2, α1(2)=3 (et donc α2(2)=1, α1(3)=2) les autres relations étant libres. Cette G-carte est clairement orientable, et pourtant HG est composée de trois composantes connexes car chaque brin de HG est totalement isolé.
La n-carte HG est une carte combinatoire. En effet, nous savons que la composition de deux permutations partielles est une permutation partielle, et il est facile de prouver que les αi•∘ α0, pour 2≤ i≤ n, sont des involutions partielles sans point fixe (en utilisant la propriété des G-cartes disant que les αi ∘ α0 sont des involutions, le fait que α0 soit sans point fixe, et la contrainte sur les αi∘α0 qui sont sans point fixe).
Les deux définitions de G-carte orientable sont équivalentes dans le cas d’une G-carte fermée puisqu’il n’y a alors aucun brin b qui soit point fixe, et donc les αi• sont tous égaux aux αi. Par contre, pour une G-carte ouverte, le fait de transformer les involutions en involutions partielles modifie la liaison des brins libres qui sont maintenant reliés à є. De ce fait, la composition αi•∘ α0 pour ce type de brin sera égale à є (car є est lié avec lui même pour chaque involution partielle) et contrairement à précédemment nous n’obtenons pas un brin appartenant à l’orientation inverse.
La conversion de G-carte en carte s’étend maintenant directement pour les cartes ouvertes (cf. Def. 41), en utilisant à nouveau la conversion entre les involutions et les involutions partielles.
De manière informelle, pour convertir une G-carte G en carte, nous prenons seulement les brins de G appartenant à la même orientation et relions ces brins par les βi correspondant aux α0i. Nous pouvons voir Fig. 2.27 un exemple de conversion d’une G-carte en carte.
[a][b]
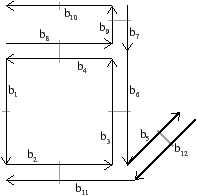
Figure 2.27: Un exemple de conversion de G-carte en carte. (a) Une carte généralisée 2D. (b) La carte combinatoire correspondante.
Nous pouvons vérifier sur cet exemple que la conversion est correctement effectuée pour les brins 1-libres et pour les brins 2-libres (les brins 0-libres étant interdits par définition, et pour les brins non libres la définition se ramène à la définition originale). Par exemple, α0(b10) est 1-libre, nous avons donc α1•∘ α0(b1)=є et donc β1(b10)=є ; α0(b1) est 2-libre, nous avons donc α2•∘ α0(b1)=є et donc β2(b1)=є.
Pour définir la conversion d’une carte en G-carte (cf. Def. 42), nous ne pouvons pas utiliser un principe similaire à celui utilisé pour la conversion de G-carte en carte qui consisterait à transformer une permutation partielle en permutation, car nous devons différencier les brins libres des autres. À part cette distinction, le principe de cette conversion est identique à la définition correspondante dans le cadre des cartes fermées.
| bi | si bi est 0-libre |
| α0(β0(bi)) | sinon |
| ci | si bi est 1-libre |
| β1(bi) | sinon |
| ∀ j: 2 ≤ j ≤ n : |
| |||||||
| ||||||||
Pour un brin bi non j-libre (1≤ j ≤ n), cette définition est identique à la définition initiale. Pour un brin bi j-libre, nous ne pouvons pas utiliser une conversion de la permutation partielle en permutation, car le résultat de cette conversion serait bi, et comme nous utilisons ensuite α0 nous obtiendrions αj(bi)=ci alors que nous devons avoir αj(bi)=bi. Pour éviter ce problème, nous testons simplement si le brin bi est j-libre et fixons dans ce cas les α correspondants de bi et de ci à bi et ci, ce qui indique que ces brins sont libres.
Pour illustrer cette transformation, il suffit de regarder l’exemple de la Fig. 2.27 dans l’autre sens : la carte combinatoire de départ est celle de la Fig. 2.2.5 et le résultat de la transformation est la G-carte de la Fig. 2.2.5. Nous pouvons vérifier sur cet exemple que la transformation est correcte pour les brins libres (le cas des brins non libres se ramène à la définition originale). Par exemple, b8 est 0-libre, nous avons donc α1(b8)=b8 ; b10 est 1-libre, et nous avons donc α1(c10)=c10 (avec c10=α0(b10)) ; et b1 est 2-libre, et donc α2(b1)=b1 et α2(c1)=c1 (avec c1=α0(b1)).
Comme n’importe quelle carte combinatoire ouverte peut être convertie en carte généralisée, et comme une G-carte représente une quasi-variété, cela prouve directement que n’importe quelle carte combinatoire ouverte correspond également à une quasi-variété. De plus, ces méthodes de conversion nous permettent, dans la suite de cette présentation, de travailler indifféremment avec une carte combinatoire ou une carte généralisée orientable. Cela nous permettra, par exemple, de travailler avec des G-cartes pour définir les opérations de base en dimension quelconque, afin de profiter de leur homogénéité, puis de travailler avec des cartes combinatoires pour définir les modèles de représentation d’images qui ont des contraintes d’espace mémoire.
Les cartes combinatoires et les cartes généralisées représentent seulement la topologie des objets, c’est-à-dire les cellules et les relations d’incidence et d’adjacence. Mais la plupart des applications ont besoin également de représenter la géométrie de ces objets, par exemple pour les afficher, pour calculer des caractéristiques de forme, de taille…Il nous faut donc associer un modèle géométrique aux cartes. Pour cela, nous pouvons associer un élément géométrique de dimension i à chaque i-cellule de la carte. Nous appelons plonger l’opération qui consiste à associer un modèle géométrique à un modèle topologique, et nous parlons du plongement d’un modèle topologique pour désigner le modèle géométrique associé.
Par exemple, en dimension 2, nous pouvons associer à chaque sommet topologique (0-cellule) un point de ℝ2. Ce plongement peut suffire pour représenter totalement la géométrie des objets ayant un plongement linéaire, c’est-à-dire tels que chaque arête corresponde à un segment de droite, chaque face soit une portion d’un plan…. Dans ce cas, le plongement de toutes les i-cellules, ∀ i: 1≤ i ≤ n, est implicite et se déduit à partir du plongement des sommets.
Si le plongement n’est pas linéaire, le plongement des sommets ne suffit pas pour déduire le plongement des autres cellules. Nous devons alors plonger chaque i-cellule topologique dans un objet géométrique ouvert de dimension i. Cet objet doit être ouvert, car le plongement du bord de la i-cellule topologique est représenté par le plongement de ses (i−1)-cellules incidentes. Il faut également satisfaire à des contraintes d’incidence pour que le plongement soit cohérent avec le modèle combinatoire (par exemple une contrainte liant le plongement d’un sommet avec l’extrémité du plongement des arêtes incidente à ce sommet). Pour cette même raison, les plongements ne doivent pas avoir d’intersections (en dehors de leurs bords) car nous n’avons alors plus de lien entre la partition du modèle combinatoire, et la partition géométrique donnée par le plongement.
Cette distinction topologie/géométrie est un des points fort des cartes. En effet, selon les algorithmes, nous allons pouvoir effectuer certains traitements en utilisant uniquement la topologie, en oubliant la géométrie correspondante (comme par exemple le calcul de propriétés topologiques comme la caractéristique d’Euler-Poincaré), et à l’inverse effectuer des traitements portant uniquement sur la géométrie, sans modifier la carte (comme par exemple la translation d’un objet). Même dans le cas d’un algorithme «mixte» travaillant à la fois sur la topologie et la géométrie, cette séparation va simplifier les accès aux informations et les modifications.
Le lien entre les cartes (combinatoires et généralisées) et les ensembles semi-simpliciaux est important car il permet de faire des rapprochements avec les nombreux travaux de topologie algébrique basés sur les complexes simpliciaux, et il permet de donner une interprétation topologique aux cartes. En effet, les ensembles (semi)-simpliciaux ont été beaucoup étudiés, et leurs propriétés topologiques sont bien connues. Ce lien permet par exemple, comme illustré dans la Section 2.3.3, d’utiliser cette conversion pour définir la caractéristique d’Euler-Poincaré des cartes (combinatoires et généralisées).
L’association entre carte généralisée et ensemble semi-simplicial est définie dans [Lie94] de la manière suivante.
Chaque brin est associé à un n-simplexe (cas où i=n ce qui implique I={α0,…,αn}). Deux brins b1 et b2 en relation par αj (0 ≤ j ≤ n) correspondent à deux n-simplexes s1=φn(b1) et s2=φn(b2) qui sont adjacents et partagent un (n−1)-simplexe s tel que djn(s1)=s et djn(s2)=s. En effet, la seconde condition pour i=n indique que ∀ j : 0≤ j≤ n, djn(φn(b1))=φn−1(⟨αj⟩(b1)) et que djn(φn(b2))=φn−1(⟨αj⟩(b2)). Comme b1=αj(b2), alors ⟨αj⟩(b1)=⟨αj⟩(b2) et donc djn(φn(b1))=djn(φn(b2)). De ce fait, chaque opérateur de face djn correspond à αj. Il est prouvé dans [Lie94] que K est bien un ensemble semi-simplicial en montrant que les opérateurs de face vérifient bien les contraintes nécessaires.
Nous montrons Fig. 2.28 un exemple de conversion de 2G-carte en ensemble semi-simplicial. Nous voyons sur cet exemple que les opérateurs de face di2 sont l’analogue des αi pour la G-carte. En 2D, les 0-simplexes correspondent aux orbites ⟨α0,α1⟩, ⟨α0,α2⟩, et ⟨α1,α2⟩ (par exemple le 0-simplexe a correspond à l’orbite ⟨α1,α2⟩(21)={21,24,26,27}, b correspond à l’orbite ⟨α0,α2⟩(26)={25,26,27,28} et c correspond à l’orbite ⟨α0,α1⟩(21)={15,16,17,18,21,22,25,26}), les 1-simplexes aux orbites ⟨α0⟩, ⟨α1⟩ et ⟨α2⟩ (par exemple le 1-simplexe [ab] correspond à l’orbite ⟨α2⟩(26)={26,27}, [ac] correspond à l’orbite ⟨α1⟩(21)={21,26}, et [bc] correspond à l’orbite ⟨α0⟩(25)={25,26}), et les 2-simplexes aux orbites ⟨⟩ (c-à-d aux brins).
[a][b]
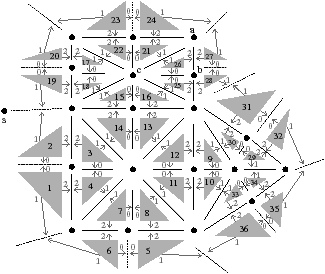
Figure 2.28: Conversion d’une carte généralisée en un ensemble semi-simplicial. (a) Une carte généralisée 2D. (b) L’ensemble semi-simplicial correspondant. Chaque 2-simplexe est numéroté avec le numéro du brin correspondant. Trois 0-simplexes sont nommés a,b et c. Les opérateurs de face sur les 2-simplexes sont représentées par les flèches grises avec un numéro indiquant le i de l’opérateur de face di2.
Nous pouvons vérifier sur un second exemple, présenté Fig. 2.29, que la conversion est toujours valide pour les G-cartes ouvertes sans avoir de cas particulier ni de différence avec le cas des G-cartes fermées. C’est dû à la définition des orbites qui «fonctionne» de manière identique dans le cas des G-cartes fermées et ouvertes.
L’association entre carte combinatoire et ensemble semi-simplicial est définie dans [Lie94] en se basant sur la conversion des G-cartes en ESS, puis en utilisant le lien entre les G-cartes et les cartes. Comme nous avons étendu ici cette conversion à toute carte combinatoire ouverte ou non, nous obtenons directement l’association entre chaque carte combinatoire et un ensemble semi-simplicial correspondant. Il faut noter que comme nous passons par la conversion d’une carte en G-carte, chaque brin de la carte se retrouve associé à deux brins de la G-carte et donc à deux n-simplexes dans l’ensemble semi-simplicial. Nous montrons un premier exemple de ce type de conversion dans la Fig. 2.30.
Nous pouvons voir Fig. 2.31 un exemple de conversion de 2-carte ouverte en ensemble semi-simplicial. Nous pouvons effectuer les mêmes vérifications sur cet exemple par rapport aux liens entre les orbites et les simplexes que pour l’exemple de 2-carte fermée.
Ce principe de conversion à l’avantage d’être simple car il réutilise les travaux sur les G-cartes, mais possède comme inconvénient d’associer deux n-simplexes à chaque brin de la carte ce qui n’est pas naturel. De plus, cela rend plus difficile sa présentation car il faut nécessairement introduire les G-cartes avant de présenter cette conversion. Pour ces raisons, nous avons commencé à étudier une définition de conversion directe qui associerait un seul n-simplexe par brin de la carte. Mais cette définition semble complexe et ce travail n’a pour le moment pas encore abouti.
L’utilisation de la conversion entre les cartes (combinatoires ou généralisées) et les ensembles semi-simpliciaux nous fournit directement une manière de calculer la caractéristique d’Euler-Poincaré. En effet, la Def. 13 indique que cette caractéristique est la somme alternée du nombre de cellules de la subdivision, et l’ensemble semi-simplicial nous fournit directement le nombre de chaque i-cellule en comptant le nombre de i-simplexes.
De ce fait, que ce soit pour les cartes combinatoires ouvertes ou non, ou pour les cartes généralisées, la caractéristique d’Euler correspondante se calcule simplement en effectuant la somme alternée du nombre de simplexes de l’ensemble semi-simplicial correspondant. Nous donnons Def. 44 la définition de la caractéristique d’Euler-Poincaré d’une G-carte. Pour les cartes, il faudra préalablement passer par la phase de conversion en G-carte, puis utiliser la même définition.
| χ(G)= |
|
| (−1)iz(⟨h(αk0,…,αki)⟩). |
Cette formule est la somme alternée, pour i allant de 0 à n, du nombre de i-simplexes de l’ensemble semi-simplicial correspondant à la G-carte. Pour l’exemple de la Fig. 2.28, cette formule nous donne χ=(z(⟨α0,α1⟩)+z(⟨α0,α2⟩)+ z(⟨α1,α2⟩))−(z(⟨α0⟩)+z(⟨α1⟩)+z(⟨α2⟩))+ (z(⟨⟩)), donc χ=(4+9+7)−(18+18+18)+(36). Nous obtenons donc χ=2 : c’est la caractéristique d’Euler-Poincaré de la sphère, qui correspond bien à la subdivision représentée par la carte de la Fig. 2.3.1.
Une autre manière de calculer la caractéristique d’Euler-Poincaré d’une carte consiste à effectuer directement la somme alternée du nombre de cellules de la subdivision (cf. Def. 45 et [Lie94]).
| χc(G)= |
| (−1)iz(⟨h(αi)⟩). |
Nous notons cette deuxième version χc(G) pour caractéristique d’Euler-Poincaré cellulaire, en opposition avec la première définition qui peut-être vue comme la caractéristique d’Euler-Poincaré simpliciale, car elle utilise implicitement la conversion de G-carte en ensemble semi-simplicial.
Les deux caractéristiques sont équivalentes lorsque les trois conditions suivantes sont vérifiées [Lie94] :
Ces conditions sont nécessaires pour éviter des cas particuliers (par exemple de repliement) posant problème lors du calcul du nombre de cellules. Intuitivement, ces conditions reviennent à garantir que la G-carte représente bien un complexe cellulaire valide dans lequel il est possible d’utiliser la définition originale de la caractéristiques d’Euler-Poincaré (cf. Def. 13). La première condition évite les G-cartes ouvertes car dans ce cas il faudrait intégrer le nombre de bords au calcul. La seconde condition revient à éviter des repliements (par exemple en 3D, pour i=2, cette condition devient α2(b)∉ ⟨α0(b)⟩ ce qui revient à replier une arête sur elle-même. Cela pose un problème car nous avons alors une sorte de demi-arête qui est difficile à intégrer dans les nombres de cellules)). La troisième condition revient à imposer à chaque i-cellule d’avoir la même caractéristique d’Euler-Poincaré qu’une boule Bi (il faut noter que χ(C0)=0 pour toute composante d’une 0G-carte fermée, et que χ(C1)=2 pour toute composante d’une 1G-carte fermée). Ces explications sont pour le moment uniquement intuitives et ce travail doit être approfondi afin d’étudier plus précisément les conséquences de ces conditions. Il faut noter que la deuxième condition inclut notre condition supplémentaire pour la conversion de G-carte en carte (condition liée à l’interdiction de point fixe dans les cartes). C’est une raison supplémentaire indiquant que notre nouvelle condition n’est pas limitante.
Pour l’exemple de la Fig. 2.28, les trois conditions sont satisfaites et les deux définitions sont donc équivalentes. Nous avons χc(G)=7−9+4=2 (sommets-arêtes+faces) et nous avons bien χc(G)=χ(G). Par contre, dans le cas présenté Fig. 2.29, nous avons χ(G)=21−48+28=1, alors que χc(G)=7−9+5=3. Les deux caractéristiques ne sont pas égales car la G-carte n’est pas fermée. De ce fait la caractéristique cellulaire n’est ici pas valide.
L’avantage de cette seconde définition est que le nombre d’orbites à calculer est moindre que dans le premier cas (par exemple en 2D nous avons trois orbites à calculer au lieu de sept dans le cas simplicial). Il serait intéressant d’étudier plus en détail ces conditions pour mieux comprendre le lien entre les G-cartes les vérifiant et les complexes cellulaires. Cela amènerait peut-être à la définition d’une sous-catégorie de cartes qui auraient alors de «bonnes propriétés». En effet, les cellules non homéomorphes à des boules sont souvent la cause de problèmes, et définir cette catégorie de G-cartes serait intéressant car cela garantirait de les éviter. Il en est de même pour les repliements.
Dans ce chapitre nous avons tout d’abord présenté les notions de base de topologie algébrique qui vont servir durant tout ce mémoire, ce qui nous a permis d’introduire les complexes simpliciaux et cellulaires. Nous avons ensuite présenté les modèles combinatoires permettant de représenter ces notions abstraites : ils sont au cœur de nos travaux et nous avons donc détaillé les cartes combinatoires et les cartes généralisées en présentant la plupart des notions existantes et en montrant de manière précise le lien entre ces modèles et les ensembles semi-simpliciaux.
L’apport principal de ce chapitre est de regrouper en un même point la majeure partie des notions existantes autour des cartes. Nous avons essayé également d’éclaircir certaines de ces notions, soit en les illustrant, soit en détaillant certaines preuves. Nous avons également profité de ce chapitre pour présenter en détail les cartes combinatoires ouvertes et les notions associées. Cela nous a amené à revisiter légèrement les cartes combinatoires en ajoutant la contrainte sur les βi sans point fixe. De notre point de vue, cette contrainte est peu limitante car elle interdit uniquement des cas très particuliers, mais clarifie et homogénéise les relations entre les trois modèles à base de carte. De plus, nous avons présenté de manière détaillée les cartes combinatoires ouvertes qui généralisent les cartes combinatoires en autorisant les bords. De ce fait, cette notion devrait remplacer la notion précédente de carte combinatoire.
Nous aurions pu également parler des chaînes de cartes [EL93, EL94] qui permettent de représenter des complexes cellulaires quelconques, c’est-à-dire des objets dont chaque cellule est une quasi-variété, mais dont l’assemblage de ces cellules est quelconque, mais nous ne l’avons pas fait afin de ne pas alourdir encore plus ce chapitre, sachant que nous n’utilisons pas ces chaînes de cartes dans la suite de ce travail.
Ce chapitre étant principalement des rappels de notions existantes, il existe peu de perspectives, mais il en existe quand même une qui est très importante et qui concerne l’étude de la caractérisation combinatoire des boules. Ce problème transparaît lors de la définition de la caractéristique d’Euler-Poincaré cellulaire pour laquelle des contraintes ont été ajoutées. Nous souhaitons étudier plus précisément ces contraintes et leurs liens avec le complexe cellulaire sous-jacent. Cette étude passe éventuellement par la définition d’une sous-classe d’objets, et par une définition précise du lien entre les modèles à base de carte et les CW-complexes. Une seconde perspective concerne le lien entre les G-cartes et les cartes ouvertes. Nous avons évoqué le problème posé par les points fixes pour les cartes, qui se pose également pour les G-cartes lorsque nous composons des involutions. Nous souhaitons donc étudier la possibilité de modifier la définition des G-cartes pour remplacer l’utilisation des points fixes par l’utilisation d’involutions partielles. Il faut pour cela comparer précisément les deux possibilités et l’impact sur l’ensemble des définitions existantes afin de mesurer les avantages et inconvénients de cette possible deuxième approche. Une dernière perspective concerne le lien direct entre les cartes combinatoires et les ensembles semi-simpliciaux. Cette définition directe simplifierait les algorithmes de calcul de caractéristiques d’Euler-Poincaré d’une carte combinatoire en évitant la phase de conversion de carte en G-carte.
Nous avons maintenant toutes les connaissances nécessaires pour définir dans le chapitre suivant les opérations de base permettant de modifier une G-carte. De plus, les différentes preuves de conversion entre les cartes combinatoires et les cartes généralisées nous permettent de donner ces définitions uniquement pour les G-cartes, en sachant qu’elles seront alors automatiquement transposables aux cartes.
Afin de modifier une carte, nous définissons quatre opérations de base : la suppression de cellules, et l’opération duale, la contraction [DL03, DDLA05] qui permettent de simplifier la carte en diminuant son nombre de cellules. Nous définissons également les opérations inverses : l’insertion de cellules, et l’opération duale, l’éclatement [BDSM08] qui permettent d’ajouter des cellules (cf. la Fig. 3.1 pour le lien entre ces quatre opérations). Nous définissons ces opérations sur les cartes généralisées pour profiter de leur homogénéité, mais ces définitions se transcrivent de manière directe sur les cartes combinatoires en utilisant les algorithmes de conversion présentés au chapitre 2.
Pour chaque opération, nous privilégions la généricité en définissant ces opérations en toute dimension et pour des cellules quelconques, la seule contrainte étant que l’application de l’opération préserve les contraintes des cartes. Nous introduisons pour cela la notion de cellule supprimable (resp. contractible) pour une cellule qui peut être supprimée (resp. contractée) et donner comme résultat une G-carte valide. Par contre, en fonction des applications, il est ensuite souvent nécessaire d’ajouter des contraintes supplémentaires afin de préserver des propriétés spécifiques comme par exemple la connexité. Mais ajouter ces contraintes se fait simplement en testant certaines propriétés avant d’appliquer l’opération, qui elle reste inchangée. L’avantage de cette approche est de fournir une opération générique pouvant servir dans n’importe quel cadre. De plus, le fait de ne pas ajouter de contrainte permet à l’utilisateur de l’opération de factoriser le test de validité à un ensemble d’opérations ce qui permet d’optimiser les temps de calculs. Ces opérations peuvent être vues comme l’analogue des opérateurs d’Euler (cf. Section 3.4), généralisés en dimension quelconque. Un autre avantage de nos définitions génériques est que les quatre opérations de base englobent les nombreuses opérations d’Euler existantes (il en existe 99 en 2D).
Une dernière opération de base qui est un peu différente des quatre autres est le décalage d’arêtes [Dam01, Dam08]. Elle est différente car elle ne simplifie pas la subdivision, ni ne la complexifie, mais va la modifier en préservant certaines propriétés. Son principe consiste à «faire glisser» une arête le long d’une arête voisine. De ce fait, elle peut servir à rendre supprimable une cellule qui ne l’était pas. Cette opération est également spéciale car elle n’est pas générique. En effet, elle est pour le moment limitée aux arêtes en 2D et 3D, et liée aux conditions de la définition de cellule supprimable. Il serait intéressant de généraliser cette opération à toute dimension, à toute cellules (décalage de face, de volume...), mais aussi de proposer l’opération duale en lien avec la définition de cellule contractible.
Il faut noter que les quatre opérations de base existaient déjà (définies dans [Elt94]) de manière totalement générique, c’est-à-dire sans contrainte sur les cellules utilisées dans les opérations. De ce fait, les définitions sont très complexes et difficilement exploitables en pratique. De plus, le contrôle de ces opérations est délicat, car pour respecter les contraintes des cartes, l’application d’une opération peut avoir des conséquences difficile à prévoir sur de nombreuses autres cellules. C’est pour résoudre ces problèmes que nous avons re-défini ces opérations, en nous limitant aux cellules supprimable et contractible, afin d’obtenir une opération générale beaucoup plus simple à définir et à utiliser.
Ce chapitre est organisé de la manière suivante. Nous commençons Section 3.1 par introduire les notions préliminaires utilisées lors de la définition des opérations. Puis nous définissons, Section 3.2, les opérations de suppression et de contraction, que nous généralisons ensuite pour la suppression/contraction simultanées d’un ensemble de cellules. Dans la Section 3.3, nous définissons les opérations inverses d’insertion et d’éclatement, ainsi que la généralisation pour l’insertion/éclatement simultanées d’un ensemble de cellules. Nous montrons le lien entre les opérations de suppression et contraction en 2D et les opérations d’Euler dans la Section 3.4. L’opération de décalage d’arête est définie dans la Section 3.5. Enfin, la Section 3.6 conclut ce chapitre et présente des perspectives.
Lors de la définition des opérations de base, nous allons fixer des contraintes afin de garantir la validité de la carte obtenue après application de ces opérations. Ces contraintes sont basées sur les notions de degré et de co-degré d’une i-cellule.
Remarquons que le degré d’une n-cellule n’est pas défini pour une carte de dimension n. De plus, le degré d’une i-cellule c ne peut jamais être égal à zéro, car il existe au moins un brin dans cette cellule, et donc au moins une (i+1)-cellule incidente à c. Enfin, le degré d’une (n−1)-cellule dans une carte de dimension n, est forcément égal à un ou deux, étant donné que nous représentons uniquement des quasi-variétés (et il ne peut donc pas y avoir plus de deux n-cellules incidente à une (n−1)-cellule). Par définition des cellules, le degré d’une i-cellule c est égal à |{ci+1(b)|b ∈ c}|. En effet, comme deux (i+1)-cellules sont soit disjointes, soit confondues, l’ensemble considéré contient bien les cellules distinctes incidentes à c et son cardinal est bien le degré de c.
De manière duale, nous allons nous intéresser au nombre de (i−1)-cellules distinctes incidentes à une i-cellule donnée, c’est la notion de co-degré (appelé parfois degré inférieur ou degré dual).
De manière duale par rapport au degré, le co-degré d’une 0-cellule n’est pas défini et le co-degré d’une 1-cellule (donc une arête) est forcément égal à 1 ou 2 : une arête à toujours exactement un ou deux sommets incidents. Comme pour le degré, le co-degré d’une i-cellule c est égal à |{ci−1(b)|b ∈ c}|.
Nous pouvons voir des illustrations des notions de degré et co-degré sur la Fig. 3.2. Par exemple, la face f1 est de co-degré un car elle est incidente à une seule arête, et le sommet s1 est de degré deux car il est incident à deux arêtes distinctes.
Nous allons également utiliser par la suite la notion d’arête pendante présentée Def. 48. Intuitivement, une arête est pendante si une de ses extrémités n’est pas rattachée à une autre arête, tandis que l’autre extrémité est rattachée à une autre arête. Toujours intuitivement, une arête pendante peut-être vue comme l’extrémité d’un chemin. Plus formellement, cela veut dire qu’un de ses sommets est incident uniquement à cette arête, ou dit autrement que le degré d’un de ses sommets est 1. Dans cette définition, une boucle n’est pas considérée comme pendante car les deux sommets de l’arête sont incident uniquement à cette arête. Il en est de même pour une arête isolée qui n’est pas non plus considérée comme pendante.
Comme chaque cellule d’une carte est défini par un ensemble de brins, une cellule c1 est uniquement incidente à c2 si c1 ⊆ c2.
Sur l’exemple de la Fig. 3.2, l’arête a3 est pendante. En effet, le sommet s3 est incident uniquement à a3, et le second sommet s2 est incident à au moins une autre arête que a3 (dit autrement, s3 est de degré un et s2 est de degré supérieur à un).
Intuitivement et de manière générale dans une carte de dimension n, la suppression d’une i-cellule consiste à supprimer cette cellule, et à fusionner éventuellement entre elles les deux (i+1)-cellules lui étant incidentes (cf. exemples Fig. 3.3 et Fig. 3.4). La contraction d’une i-cellule est l’opération duale de la suppression. Elle consiste à contracter cette cellule en une (i−1)-cellule (cf. exemple Fig. 3.5). Dans une carte de dimension n, la suppression est donc définie pour les cellules de dimension 0 à n−1, et la contraction pour les cellules de dimension 1 à n.
Figure 3.3: Exemples de suppression en 2D. (a) Une subdivision 2D initiale. (b) Le résultat après la suppression de l’arête a2. Les deux faces f1 et f2 sont fusionnées en une seule face f. (c) Le résultat après la suppression du sommet s1: les deux arêtes a1 et a3 sont fusionnées en une seule arête a. La suppression n’est applicable qu’aux cellules de degré inférieur ou égal à deux : la suppression de s1 n’était donc pas possible dans la subdivision initiale, car son degré était trois, mais elle est devenue possible après la suppression de a2 qui a entraîné la diminution du degré de s1.
Figure 3.4: Exemples de suppression en 3D. (a) Une subdivision 3D initiale. (b) Le résultat après la suppression de la face grise foncée. (c) Le résultat après la suppression de l’arête a1.
Figure 3.5: Exemples de contraction en 2D. (a) Une subdivision 2D initiale. (b) Le résultat après la contraction de la face f. Les deux arêtes a1 et a2 ont fusionnées en une seule arête a. (c) Le résultat après la contraction de l’arête a: les deux sommets s1 et s2 ont fusionnés en un seul sommet s.
Pour qu’une i-cellule c puisse être supprimée, il faut qu’il y ait au plus deux (i+1)-cellules incidentes à c. En effet, il est autrement impossible de savoir automatiquement comment recoller entre elles les cellules incidentes à c en conservant la propriété de quasi-variété des cartes.
Par exemple, la suppression du sommet s1 de la Fig. 3.2 qui est incident aux trois arêtes a1, a2 et a3, devrait entraîner la création d’une hyper-arête étant l’union des trois, ce qui n’est pas représentable avec une carte.
Ajouter une précondition sur la cellule à supprimer permet de résoudre ces problèmes, sans limiter les possibilités offertes à l’utilisateur. En effet, il est ensuite possible de faire une opération de plus haut niveau enchaînant une suite d’opérations atomiques, chacune respectant les préconditions de l’opération de base (sur l’exemple de la Fig. 3.2, nous pouvons envisager une opération de plus haut-niveau permettant de supprimer s1 en commençant par supprimer une arête lui étant incidente).
Cette contrainte intuitive se traduit en pratique par la définition de cellule supprimable.
Remarquons que la précondition de l’opération ne s’applique pas pour i=n−1 (car n+1 n’existe pas dans une carte de dimension n) : une n−1 cellule peut toujours être supprimée dans une nG-carte. En effet, les cartes représentant des quasi-variétés, une (n−1)-cellule est toujours incidente à au plus deux n-cellules dans une nG-carte, et peut donc toujours être supprimée. Par contre une n-cellule c n’est jamais supprimable car il n’existe pas de (n+1)-cellules incidentes à c à fusionner.
L’opération de i-suppression dans une nG-carte peut maintenant être définie (cf. Def. 50). Pour supprimer une i-cellule c dans une G-carte donnée, il suffit de redéfinir les involutions αi des brins qui sont i-voisins de c (notés BV). Cette redéfinition est locale et nécessite uniquement un parcours des brins de c.
Lors de la redéfinition des αi pour les brins de BV, nous utilisons un chemin de brins défini par ( αi αi+1 )k αi. Ce chemin permet, à partir d’un brin de b′ ∈ BV, de rentrer dans la cellule supprimée (en utilisant αi) puis de traverser cette cellule (en utilisant αi+1 et αi jusqu’à sortir de la cellule supprimée). Il faut éventuellement itérer ces deux dernières involutions (ce qui explique le k) afin de traiter le cas où la cellule est repliée sur elle-même (cas des multi-incidences cf. l’exemple d’une boucle en 2D Fig. 3.9).
Remarquons que pour les brins b′ ∈ B′−BV, b′αi′=b′(αiαi+1)kαi avec k=0 qui est le plus petit entier tel que b′αi′ ∈ BV.
Nous pouvons voir différents exemples de suppression dans les Figs. 3.6 à 3.9 : tout d’abord un exemple de 0-suppression en 1D (Fig. 3.6), puis de 0-suppression en 2D (Fig. 3.7), de 1-suppression en 2D (Fig. 3.8) et enfin un cas de multi-incidence où k=2 (Fig. 3.9).
[a][b]
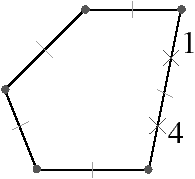
Figure 3.6: 0-suppression en 1D. (a) La 1G-carte initiale. c=⟨α1⟩(2)={2,3} (les brins marqués avec □), cα0={1,4} = BV (les brins marqués avec ×). (b) Le résultat après la 0-suppression. La 0-suppression consiste simplement à définir 1α0′=1(α0α1)α0=4 ∈ BV et 4α0′=4(α0α1)α0=1 ∈ BV.
Figure 3.7: 0-suppression en 2D. (a) La 2G-carte initiale. c=⟨α1,α2⟩(2) (les brins marqués avec □), cα0 = BV (les brins marqués avec ×). (b) Le résultat après la 0-suppression. Par exemple, 1α0′=1(α0α1)α0=4 ∈ BV
[a][b]

Figure 3.8: Cas général de la 1-suppression en 2D. (a) La 2G-carte initiale. Les brins de l’arête à supprimer sont marqués avec ∘. (b) Le résultat après la 1-suppression.
[a][b]
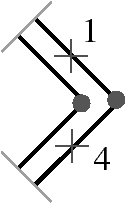
Figure 3.9: 1-suppression en 2D dans un cas de multi-incidence : ici une boucle. (a) La 2G-carte initiale. (b) Le résultat après la 1-suppression. Par exemple, 1α′1=1(α1α2)(α1α2)α1=4 ∈ BV (car 1(α1α2)α1 ∉BV, ce brin appartient à c et à cα1).
Dans le cas général, lorsque la i-cellule c supprimée est incidente à deux (i+1)-cellules distinctes c1 et c2, et qu’aucune (i−1)-cellule incidente à c n’est de degré un, l’opération de suppression entraîne la disparition de la cellule c et la fusion des deux cellules c1 et c2 en une seule cellule. Il n’y a pas d’autre disparition ou fusion de cellules. De ce fait, la caractéristique d’Euler-Poincaré généralisée reste inchangée au cours de l’opération car le nombre de cellules diminue d’un pour deux dimensions consécutives (i et i+1), et ces nombres sont additionnés avec des signes opposés dans la formule d’Euler-Poincaré.
Par contre, lorsque la i-cellule supprimée c est incidente deux fois à la même cellule c1=c2 (c-à-d c est de degré un), plusieurs cas peuvent se produire, entraînant ou non des modifications topologiques. Ces cas dépendent de la présence et de la position de (i−1)-cellules de degré un incidentes à c (ces configurations et l’impact des suppressions sur les modifications topologiques sont détaillés Section 6.2). Mais dans tout ces cas, même s’il y a changement de topologie, l’opération est valide car nous pouvons prouver que son résultat est toujours une nG-carte. Il en est de même si la suppression entraîne une déconnexion en plusieurs composantes connexes, voire même si le résultat est une carte vide (par exemple dans le cas d’une G-carte composée d’une seule arête qui est supprimée). Ce sera ensuite les applications qui selon le cadre d’utilisation auront à charge d’ajouter des contraintes pour satisfaire leurs besoins spécifiques.
L’opération de contraction se définit de manière similaire à l’opération de suppression. En effet, la i-suppression est l’opération duale de la (n−i)-contraction. En utilisant la définition de G-carte duale (Def. 32), nous pouvons transformer la définition de la i-suppression en définition de la (n−i)-contraction simplement en remplacant les indices i par (n−i), i+1 par (n−i−1) et i+2 par (n−i−2). Pour obtenir la définition de la i-contraction et non de la (n−i)-contraction, il faut ensuite renommer (n−i) en i, et donc remplacer (n−i−1) par i−1 et (n−i−2) par i−2. Ces remplacements doivent être faits dans la définition de cellule supprimable qui devient la définition de cellule contractible, ainsi que dans la définition de l’opération de suppression qui devient l’opération de contraction.
Nous pouvons voir deux exemples de contraction dans les Figs. 3.10 et 3.11 : le premier montrant la contraction d’une arête dans une 1G-carte et le second une contraction d’arêtes dans une 2G-carte.
[a][b]
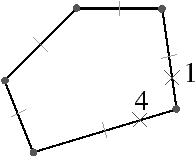
Figure 3.10: 1-contraction en 1D. (a) La 1G-carte initiale. Les brins de l’arête contractée sont marqués avec •, et ceux de BV avec ×. (b) Le résultat après la 1-contraction.
[a][b]
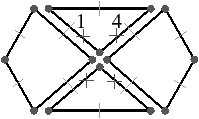
Figure 3.11: 1-contraction en 2D. (a) La 2G-carte initiale. Les brins de l’arête contractée sont marqués avec •, et ceux de BV avec ×. (b) Le résultat après la 1-contraction.
Comme pour la suppression, la contraction d’une i-cellule c peut entraîner des modifications topologiques ou non selon les configurations, et peut entraîner des suppressions d’autres cellules incidentes à c, la différence étant que par dualité, il faudra s’intéresser aux (i+1)-cellules incidentes à c (et non plus aux (i−1)-cellules comme pour la suppression)
Les deux définitions précédentes permettent d’effectuer la suppression ou la contraction d’une seule cellule. Il est intéressant de pouvoir effectuer plusieurs opérations simultanément, pour des raisons de flexibilité et d’efficacité. Pour cela, il faut marquer les cellules à supprimer et à contracter, avec la dimension et le type de l’opération. Les opérations peuvent être appliquées simultanément si les cellules sont disjointes et si chaque cellule vérifie la précondition éventuelle des opérations unitaires. La G-carte résultante peut alors être calculée directement, les α′ se définissant en une seule fois à l’aide de chemins de brins supprimés et contractés dans la carte initiale.
| i+1 si bj = b(αiαl1) … (αiαlj−1)αi ∈ Si, |
| i−1 sinon (bj ∈ Ci) . |
Chaque brin est marqué avec la dimension et le type de l’opération appliquée sur la cellule incidente. Tester si les cellules sont disjointes revient simplement à vérifier que chaque brin est marqué avec au plus une seule opération.
De manière intuitive, pour chaque brin b ∈ BVi, nous «parcourons» les brins de la G-carte en partant de bαi et appliquant soit (αi+1αi) si le brin courant appartient à une cellule supprimée, soit (αi−1αi) si le brin appartient à une cellule contractée. Nous arrêtons le parcours dès que le brin courant n’appartient ni à une cellule supprimée ni à une cellule contractée. Nous avons alors trouvé la nouvelle image par αi du brin de départ (nous retrouvons ici la notion de chemin de connexion introduite en 2D dans [BK02] et détaillée au chapitre 5).
Ce principe utilise le fait que les cellules sont disjointes : chaque brin rencontré durant le parcours est marqué avec au plus une seule opération, il n’y a donc aucune ambiguïté sur le type d’opération. Cette précondition implique que, à partir de b ∈ BVi, nous allons parcourir uniquement des i-cellules supprimées et/ou des i-cellules contractées. En effet, c’est le cas pour la première cellule rencontrée incidente à b αi (par définition de BVi) et c’est le cas de proche en proche pour les cellules parcourues. Plus précisément, soit b′ appartenant à une i-cellule supprimée (resp. contractée) : b″=b′αi+1 (resp. b″=b′αi−1) appartient à la même i-cellule (par définition des i-cellules). Supposons b‴=b″αi ∉ BVi et la dimension de l’opération associée à b‴ soit j ≠ i. Comme b″ et b‴ appartiennent à la même j-cellule (car ils sont reliés par αi), b″ est marqué avec deux opérations différentes ce qui contredit la précondition sur les cellules disjointes.
Pour la même raison, nous pouvons observer que les chemins reliant deux brins quelconques pour deux dimensions différentes sont disjoints, sauf éventuellement à leurs extrémités. En effet, un brin peut appartenir à plusieurs BVi différents lorsqu’il est voisin de plusieurs cellules de dimension différentes contractées ou supprimées. Par contre, les chemins sont disjoints grâce à la précondition sur les cellules disjointes.
Cette remarque nous permet de garantir que la carte résultante est indépendante de l’ordre dans lequel nous redéfinissons les α′i. En effet, en pratique, il est plus simple de modifier directement la G-carte en mettant à jour ses involutions, sans avoir à la dupliquer pour définir les nouvelles involutions α′i en fonction des anciennes αi. Cette possibilité est réalisable grâce à l’indépendance des chemins par rapport à l’ordre des redéfinitions. Cette indépendance permet également d’envisager l’application en parallèle des redéfinitions.
Enfin, nous pouvons montrer que la G-carte résultante de l’application simultanée d’un ensemble de suppressions et contractions est la même celle obtenue en appliquant chaque opération unitaire de manière successive, et ce dans n’importe quel ordre. Le principe de la démonstration repose à nouveau sur la propriété des cellules disjointes, mais utilise également le fait que pour deux i-cellules adjacentes, le chemin traversant les deux cellules est la concaténation des deux chemins unitaires traversant chaque cellule. De ce fait, la redéfinition simultanée d’un α′i peut-être ramenée à une suite de redéfinitions successives de α′i, un pour chaque opération unitaire.
Un exemple illustrant l’opération de suppression et contraction simultanées d’un ensemble de cellules est présenté Fig. 3.12. Sur cet exemple, les quatre opérations existantes en dimension deux sont simultanément utilisées : la 1- et 2-contraction, et la 0- et 1-suppression.
[a][b]
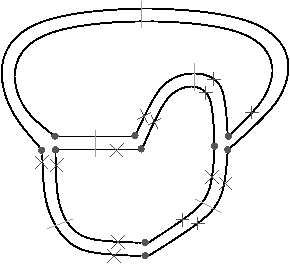
Figure 3.12: Un exemple 2D de suppression et contraction simultanées de cellules de différentes dimensions. (a) La 2G-carte initiale. Les brins appartenant à une 1-cellule supprimée (resp. 0-cellule supprimée, 1-cellule contractée, 2-cellule contractée) sont marqués avec ∘ (resp. □, •, filled square). Les brins marqués avec × appartiennent à ∪ BVi. Trois chemins de connexion sont représentés : C1 qui traverse une arête contractée, C2 qui traverse deux sommets contractés, et C3 qui traverse une arête contractée puis une arête supprimée. (b) La 2G-carte obtenue après application de l’opération.
Les deux autres opérations de base, qui sont l’insertion et l’éclatement, sont les opérations inverses des opérations précédentes. Ces opérations permettent de raffiner une subdivision en y ajoutant des cellules.
Des exemples d’insertion sont présentés en 2D Fig. 3.13 et en 3D Fig. 3.14 et des exemples d’éclatement en 2D Fig. 3.15. Une comparaison entre ces exemples et les exemples similaires de suppression et de contraction permet de voir que les paramètres d’entrées de ces nouvelles opérations sont plus complexes. En effet, pour les deux opérations précédentes, la donnée seule de la cellule suffit, les modifications sont ensuite guidées par la configuration des cellules voisines données dans la carte. Pour l’insertion et l’éclatement, la donnée de la cellule ne suffit plus car il y a plusieurs manières d’ajouter cette cellule dans la subdivision existante : il faut également fournir comme paramètre de l’opération la manière de relier la nouvelle cellule à la carte existante.
Figure 3.13: Exemples d’insertion en 2D. (a) Une subdivision 2D initiale. (b) Le résultat après l’insertion du sommet s1 sur l’arête a : l’arête a été découpée en deux arêtes a1 et a3. (c) Le résultat après l’insertion de l’arête a2 entre les sommets s1 et s2. La face f a été découpée en deux faces f1 et f2.
Figure 3.14: Exemples d’insertion en 3D. (a) Une subdivision 3D initiale. (b) Le résultat après l’insertion d’une arête entre les sommets s1 et s2. (c) Le résultat après l’insertion d’une face le long des arêtes a1, a2 et a3.
Figure 3.15: Exemples d’éclatement en 2D. (a) Une subdivision 2D initiale. (b) Le résultat après l’éclatement de s en arête. Le sommet s a été éclaté dans les deux sommets s1 et s2. (c) Le résultat après l’éclatement de a en face. L’arête a a été éclatée dans les deux arêtes a1 et a2.
La définition de l’insertion d’une i-cellule dans une nG-carte s’inspire directement de la i-suppression qui est l’opération inverse. La différence principale se situe dans les données de l’opération. Nous avons maintenant G une nG-carte, c la cellule à insérer, donnée dans une deuxième nG-carte, et une involution γ explicitant comment relier les brins de G et les brins de c.
Les contraintes de la Def. 54 obligent que la cellule c soit supprimable, ceci afin que le résultat de l’insertion soit une quasi-variété mais aussi pour que l’insertion soit bien l’opération inverse de la suppression.
Remarquons que dans la définition de G′, seul αi est redéfini pour les brins de BV ∪ BV′. En effet, l’insertion entraîne la couture des brins de BV avec les brins de BV′ par αi (qui est donnée par γ). Toutes les autres involutions restent inchangées. Enfin, nous avons prouvé dans [BDSM08] que cette opération est valide, c’est-à-dire que G′ est bien une nG-carte.
La Fig. 3.16 montre un exemple d’insertion pour une cellule vérifiant les trois préconditions de l’opération (cas Fig. 3.16(c)), ainsi qu’un exemple où la troisième précondition n’est pas vérifiée (cas Fig. 3.16(a)). Pour ce dernier exemple, 3α0=4 est différent de 3γ α1 γ=3. L’insertion d’une telle cellule donne un résultat qui n’est plus une G-carte car nous modifions α0 pour le brin 3, mais pas pour le brin 4.
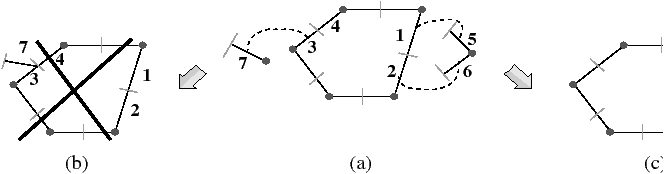
Figure 3.16: 0-insertion en 1D. (a) 1G-carte initiale G qui correspond à l’orbite ⟨α0, α1⟩ (1 ). Une 0-cellule c1 = ⟨α1⟩ ( 7) = {7}, BV1 = {3}, BV′1 = {7}. Une seconde 0-cellule c2 = ⟨α1⟩ ( 5) = {5, 6 }, BV2 = {1,2 }, BV′2 = {5,6 }. L’involution γ est représentée par les traits pointillés : γ relie respectivement les brins 1,2 et 3 avec les brins 5,6 et 7. (b) Résultat invalide après insertion de c1 dans G (α0 n’est plus une involution car 3 α0 = 7 et 4 α0 = 3). Ce cas est interdit par les préconditions de l’opération d’insertion. (c) Résultat valide après insertion de c2 dans G (la précondition b α0 = b γ α1 γ est satisfaite pour tout les brins de c2).
L’exemple de la Fig. 3.17 montre un autre cas où la troisième condition de la Def. 54 n’est pas vérifiée. En effet, 1α0=1 est différent de 1γ α1 γ=2. Dans ce cas, l’insertion de la cellule donne une G-carte valide, mais l’opération n’est alors pas l’inverse de la suppression.
[a][b]
[c]
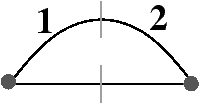
Figure 3.17: Exemple où la troisième précondition de la 0-insertion n’est pas satisfaite. (a) Une 1G-carte G et un sommet à insérer c={3,4}. L’involution γ est représentée par les traits pointillés. BV = {1,2} et BV′ = {3,4} sont deux sous-ensembles de brins, chaque brin de ces ensembles étant 0-libre. (b) La 1G-carte G′ obtenue après insertion de c dans G. (c) La 1G-carte obtenue après suppression de c dans G′: les brins 1 et 2 sont maintenant 0-cousus alors qu’ils étaient 0-libres avant l’insertion : la suppression n’est pas l’inverse de l’insertion.
La Fig. 3.18 présente deux exemples de 0-insertion dans une 2G-carte. Dans les deux cas, les trois préconditions de l’opération sont vérifiées. Cet exemple montre que la donnée explicite de l’involution γ est nécessaire car il y a plusieurs manières d’insérer la même cellule dans la même G-carte, le long des mêmes brins. Sur cet exemple, la seule différence entre les deux cas porte sur la manière dont les brins de BV et BV′ sont mis en relation.
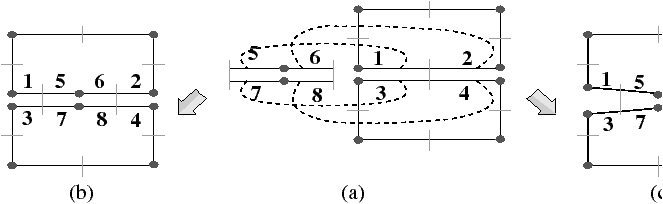
Figure 3.18: 0-insertion en 2D. (a) 0-cellule C=⟨α1,α2⟩ ( 5 ) = {5,6,7,8}, BV = {1,2,3,4}, BV′ = C. La 2G-carte initiale G égale à l’orbite ⟨α0, α1, α2⟩ ( 1). L’involution γ1 est représentée par les traits pointillés (respectivement entre les brins 1,2,3,4 et les brins 5,6,7,8) L’involution γ2 (non représentée sur la figure) relie respectivement les brins 1,2,3,4 avec les brins 5,8,7,6. (b) La 2G-carte obtenue après insertion de c dans G en utilisant l’involution γ1. (c) La 2G-carte obtenue après insertion de c dans G en utilisant l’involution γ2.
La Fig. 3.19 présente un exemple de 1-insertion dans une 2G-carte. Les trois préconditions de l’opération sont vérifiées, le résultat est une 2G-carte valide.
[a][b]
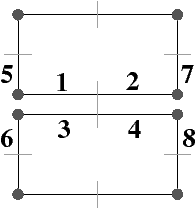
Figure 3.19: 1-insertion en 2D dans le cas général. (a) Les brins de l’arête à insérer sont numérotés de 1 à 4. L’involution γ est représentée par les traits pointillés. (b) Le résultat de l’insertion.
La Fig. 3.20 présente un second exemple de 1-insertion dans une 2G-carte mais cette fois pour un cas particulier : l’insertion d’une boucle. La seule différence avec l’exemple précédent est que ici, k=1 alors que dans les cas précédents, k était égal à 0. En effet, durant le parcours du chemin de redéfinition de α1′, il faut traverser l’arête avant de retomber sur un brin de BV′. Comme les trois préconditions de l’opération sont vérifiées, le résultat est une 2G-carte valide.
[a][b]
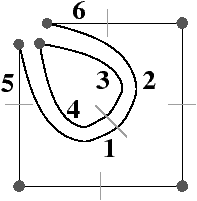
Figure 3.20: 1-insertion en 2D dans un cas particulier : ici l’insertion d’une boucle. (a) Les brins de l’arête à insérer sont numérotés de 1 à 4. L’involution γ est représentée par les traits pointillés. (b) Le résultat de l’insertion. La troisième précondition de l’opération est vérifiée car 5 α1 = 5 γ α2 ( α1 α2 ) γ =6.
De manière analogue à la contraction pour la suppression, l’opération d’éclatement se définit de manière similaire à l’opération d’insertion. En effet, le i-éclatement étant l’opération duale de la (n−i)-insertion, il suffit de remplacer les indices i+1 par (i−1) et i+2 par (i−2).
Les Figs. 3.21 et 3.22 montrent deux exemples d’éclatement, le premier en 1D et le second en 2D. Le principe est le même que pour l’insertion, la différence étant uniquement sur les préconditions de l’opération qui garantissent que l’éclatement est l’opération inverse de la contraction.
[a][b]
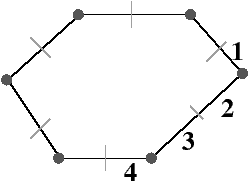
Figure 3.21: 1-éclatement en 2D. (a) Les brins de l’arête à insérer sont numérotés 2 et 3. L’involution γ est représentée par les traits pointillés. (b) Le résultat de l’éclatement.
[a][b]
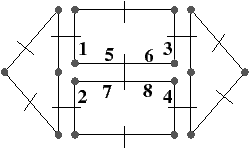
Figure 3.22: 1-éclatement en 2D. (a) La 2G-carte initiale et l’arête à insérer (brins numérotés de 5 à 8). L’involution γ est représentée par les traits pointillés. (b) Le résultat de l’éclatement.
Les deux définitions précédentes permettent d’effectuer l’insertion ou l’éclatement d’une seule cellule. Comme pour les opérations de suppression et contraction, il est intéressant de pouvoir effectuer plusieurs opérations simultanément. La donnée de l’opération généralisée est maintenant une nG-carte G et une seconde nG-carte G′ contenant l’ensemble des cellules à insérer et à éclater. Chaque brin de G′ est marqué avec la dimension et le type de l’opération (insertion ou éclatement). Les opérations peuvent être appliquées simultanément si les cellules sont disjointes et si chaque cellule vérifie la précondition éventuelle des opérations unitaires. La G-carte résultante peut alors être calculée directement, les nouvelles involutions se définissant en une seule fois à l’aide des involutions γ.
| i+1 si bj = b γi αl1 (αiαl2) … (αiαlj−1) ∈ I, |
| i−1 sinon (c-à-d bj ∈ E) . |
Comme pour l’opération de suppression et contraction simultanées, les cellules doivent être disjointes, et vérifier la contrainte d’être supprimables pour les cellules à insérer et contractibles pour les cellules à éclater. De plus, toutes les cellules de G′ doivent être marquées à insérer ou à supprimer. En effet, sans cette contrainte, l’opération ne serait pas l’opération inverse de la suppression et contraction simultanées car les brins n’appartenant à aucune cellule à insérer ou éclater ne seraient pas supprimés par l’opération de suppression et contraction. De ce fait, la carte obtenue après insertion et éclatement simultanés, puis suppression et contraction simultanées, ne serait pas isomorphe à la carte initiale.
Pour cette opération généralisée, il y a maintenant n+1 involutions γi, une par dimension de la subdivision. Chaque involution doit vérifier les préconditions de l’opération de base :
De plus, le fait que les γi soient des involutions entraîne qu’un brin b ne peut être utilisé que pour insérer ou éclater une unique i-cellule. Par contre, un même brin peut être utilisé pour plusieurs cellules de dimensions différentes.
La Fig. 3.23 montre un exemple de l’opération d’insertion et d’éclatement simultanés. Sur cet exemple, les quatre opérations existantes en dimension deux sont simultanément utilisées : les 1- et 2-éclatements, et les 0- et 1-insertions.
[a][b]
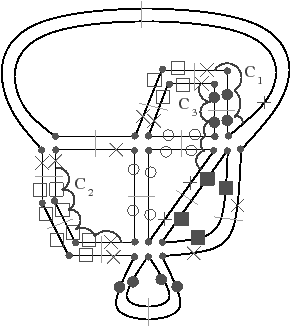
Figure 3.23: Un exemple en 2D d’insertion et éclatement simultanés de cellules de différentes dimensions. (a) La 2G-carte initiale et les cellules à insérer et éclater. Les brins appartenant à une 1-cellule insérée (resp. 0-cellule insérée, 1-cellule éclatée, 2-cellule éclatée) sont marqués avec ∘ (resp. □, •, filled square). Les brins marqués avec × appartiennent à ∪ BVi. Les involutions γi sont représentées par les traits pointillés, avec un numéro indiquant la dimension de l’opération. (b) La 2G-carte obtenue après application de l’opération.
Les opérateurs d’Euler sont les opérateurs de base permettant de modifier une variété 2D. L’intérêt de ces opérateurs est de pouvoir servir de brique de base pour modifier un objet, tout en contrôlant l’évolution de ses caractéristiques topologiques. Ces opérateurs ont été beaucoup étudiés [Bau74, EW79, BHS80, Män88, Str06] et il a été prouvé dans [Män84] que ces opérateurs forment un «ensemble complet», c’est-à-dire que n’importe quel polyèdre peut être construit par une séquence finie de ces opérateurs. Ces opérateurs sont classifiés en comptant :
La formule d’Euler-Poincaré peut s’étendre pour tenir compte des coques, des cycles internes et du nombre de bord : v − (e+l) + (f + b) = 2(s−g), avec g le genre de l’objet (cf. exemple Fig. 3.24). Intuitivement, une face est ajoutée pour chaque bord (afin de fermer les surfaces) ce qui explique le (f + b), et une arête est ajoutée pour chaque cycle interne (pour relier ce cycle au cycle externe pour se ramener au cas d’une face représenté par un seul cycle). Pour un complexe fermé b=0, ayant une seule coque s=1, et tel que chaque face soit décrite par un seul cycle l=0, nous retrouvons la formule classique donnée Section 2.1.4 : v − e + f = 2−2g.
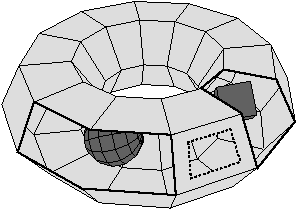
Figure 3.24: Exemple de complexe cellulaire illustrant la notion de coques, de cycles internes, et de bords. Cet objet est composé de trois coques c=3 (une pour le tore extérieur avec les faces en gris clair, une pour la sphère et une pour le cube intérieur avec les faces en gris foncé). Il y a un cycle interne l=1 (dessiné en pointillé), et trois bords b=3 (dessinés en gras, un bord correspond au cycle interne). Cet objet est composé de 158 sommets, 314 arêtes et 158 faces2. Nous obtenons donc 2(3−g)=158 − (314+1) + (158 + 3)=4 et donc g=1 : c’est bien le genre d’un tore.
Il existe 99 opérateurs d’Euler «atomiques» qui ne modifient qu’une seule des caractéristiques du complexe cellulaire (cf. [Str06] pour la liste exhaustive). Le nombre de ces opérateurs peut être réduit à 39 en considérant des combinaisons des opérateurs atomiques autorisant la modification de deux ou trois caractéristiques. Enfin, il est possible de sélectionner seulement 10 opérateurs et de prouver que n’importe quel polyèdre valide peut-être obtenu à partir de n’importe quel autre polyèdre valide en utilisant une séquence finie de ces opérateurs. Ces 10 opérateurs sont donnés Fig. 3.25. Il y a 5 opérateurs de type makeX qui ajoutent des éléments, et qui correspondent à nos insertions ou éclatements, et les 5 opérateurs inverses de type killY, qui correspondent à nos suppressions ou contractions.
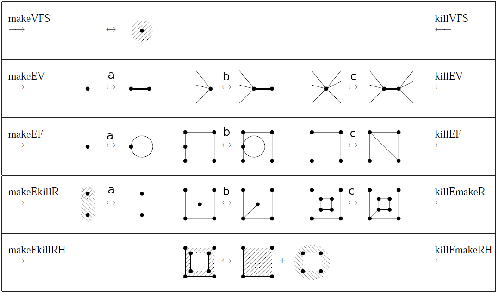
Figure 3.25: Les 10 opérateurs d’Euler permettant de créer n’importe quel complexe cellulaire. Image tirée de [Hav05].
Chaque opérateur peut s’écrire de la forme MaKb avec M pour make (construit) l’entité (ou les entités) a, et K pour kill (détruit) l’entité (ou les entités) b, et chaque entité pouvant être sommet V, arête E, face F, coquille S, bord H ou cycle interne R.
Op. Signification Op. inv. Signification MVFS make a vertex, a face and a shell KVFS kill a vertex, a face and a shell MEV make an edge and a vertex KEV kill an edge and a vertex MEF make an edge and a face KEF kill an edge and a face MEKR make an edge, kill a ring KEMR kill an edge, make a ring MFKRH make a face, kill a ring and a hole KFMRH kill a face, make a ring and a hole
Tableau 3.1: Tableau donnant la liste des 10 opérateurs d’Euler utilisés ici, et leur signification. Il y a 5 opérateurs de construction (makeX) et 5 opérateurs inverses de destruction (killY). Pour les 3 opérateurs au milieu de la Fig. 3.25, il y a 3 sous cas différents, numérotés a, b et c.
Il est facile de vérifier que chaque opérateur correspond à une de nos opérations. Tout d’abord, ces opérateurs étant défini dans le cadre des polyèdres, nous utilisons une 2G-carte. Nous allons maintenant donner pour chaque opérateur d’Euler son équivalent en terme d’opération sur cette 2G-carte.
Il arrive que dans certains cas, un même opérateur corresponde à deux opérations. En effet, dans des cas particuliers (par exemple pour une arête pendante), les cartes obtenues par l’application de deux opérations différentes sont isomorphes (la suppression ou la contraction d’une arête pendante), mais ce n’est pas vrai dans le cas général.
Pour les 5 opérateurs inverses (killY), comme nous avons vu que les suppressions et contractions sont les opérations inverses des insertions et éclatements, nous déduisons directement les opérations associées (par exemple pour l’opérateur KEF qui est l’inverse de MEF, dans les 3 cas (a), (b) et (c), 1-suppression de l’arête. Dans les cas (a) et (b), cela peut également être la 1-contraction de l’arête en sommet).
L’opération de décalage d’arête, illustrée Fig. 3.26, consiste à «pousser» le coté d’une arête le long de l’arête suivante de la même face (et du même volume si nous sommes en 3D). Cette opération est définie ici pour des configurations respectant certaines propriétés, et uniquement en 2D et en 3D.
[a][b]
[c]
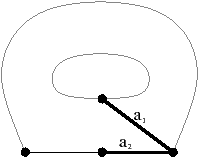
Figure 3.26: Un exemple 2D de décalage d’arête. L’arête a1 est décalée le long de l’arête a2. Il est possible de voir ce décalage comme une déformation continue passant de la configuration initiale (a) à la configuration finale (c).
Commençons tout d’abord par le cas 2D. Les contraintes à vérifier sont :
Ces contraintes assurent que la modification est locale à la face incidente à cette arête, qu’il existe bien une autre arête le long de laquelle décaler l’arête, et que l’arête le long de laquelle nous allons décaler c1(b) n’est pas une boucle.
Nous notons ac=⟨h(α0,α1)⟩(b), ce sont les brins de l’arête du coté du sommet incident à b, BV= ac α1 − ac, les brins 1-cousus à ac n’appartenant pas à ac, b2=bα2, d1=bα10 et d2=d1α1, et D={d1,d2}.
La 2G-carte obtenue en décalant l’arête a le long de l’arête suivant a du coté du sommet incident à b est G′=(B,α0′,α1′,α2′) définie par :
Cette opération de décalage d’arête peut être vue comme la suppression de l’arête, mais uniquement d’un coté de l’arête, puis comme l’insertion de cette arête sur le sommet suivant. Pour cette raison, nous retrouvons dans la Def. 57 les trois premiers points qui proviennent directement de la définition de la suppression d’arête, mais en se limitant à un seul côté de l’arête (ce qui se traduit en pratique par l’utilisation de l’orbite ⟨h(α0,α1)⟩(b) au lieu de l’orbite arête ⟨h(α1)⟩(b)), et les deux derniers points qui proviennent de la définition de l’insertion d’arête.
La Fig. 3.27 présente un exemple de décalage d’arête 2D dans le cas général. Nous souhaitons décaler l’arête incidente au brin b dans la G-carte initiale de la Fig. 3.5 sur l’arête suivante du côté du sommet incident au brin b. Ce décalage est réalisé en modifiant les relations α1′ pour les brins o1, o2, et les brins d1, d2. Le troisième point de la Def. 57 va fixer α1′(o1)=o2 et α1′(o2)=o1, et les deux derniers points de cette même définition vont fixer α1′(d1)=b2, α1′(b2)=d1, et α1′(d2)=b, α1′(b)=d2. Nous pouvons vérifier sur l’exemple que ces 6 modifications correspondent bien au décalage de l’arête.
[a][b]
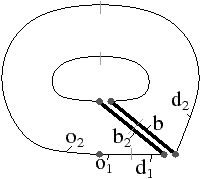
Figure 3.27: Le cas général de décalage d’arête en 2D. (a) La configuration initiale. L’arête c1(b) est à décaler. Les brins d1 et d2 donnent la position où l’arête va être décalée. Les brins o1 et o2 sont les voisins de l’arête qui vont être modifiés : BV={o1,o2}. (b) La G-carte obtenue après le décalage.
Nous pouvons vérifier sur les exemples des Figs. 3.28 et 3.29 que le décalage d’arête fonctionne correctement dans les cas particuliers où le brin b2 est 1-libre, et le cas où le brin bα10 est 1-libre. Les autres possibilités de brin libre sont interdites par les conditions de la Def. 57.
[a][b]
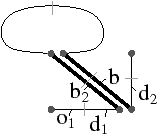
Figure 3.28: Un cas particulier de décalage d’arête en 2D lorsque le brin b2 est 1-libre. (a) La configuration initiale, avec l’arête c1(b) à décaler. (b) La G-carte obtenue après le décalage. Ce cas est traité correctement par le point 3 de la Def. 57 en fixant α1′(o1)=o1 avec k=2.
[a][b]
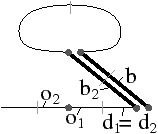
Figure 3.29: Un autre cas particulier de décalage d’arête en 2D lorsque le brin bα10 est 1-libre, ce qui entraîne d2=d1. (a) La configuration initiale, avec l’arête c1(b) à décaler. (b) La G-carte obtenue après le décalage. Ce cas est traité correctement par le point 5 de la Def. 57 en fixant α1′(b)=b.
La définition de décalage d’arête 2D s’étend directement en dimension 3. En effet, par définition des G-cartes, il existe deux cas possibles : soit l’arête à décaler est 3-libre, et alors tous les brins de la face sont 3-libres, soit l’arête à décaler n’est pas 3-libre et alors il existe deux demi-faces isomorphes ayant tout leurs brins reliés par α3 deux à deux. Dans le premier cas, la définition du décalage d’arête se ramène au cas 2D, et dans le second cas il faut effectuer deux redéfinitions : une pour chaque brin de la demi-face, et une seconde pour leurs images par α3. La Def. 58 présente cette opération de décalage d’arête en 3D.
Nous notons ac=⟨h(α0,α1)⟩(b), ce sont les brins de l’arête du coté du sommet incident à b, BV= ac α1 − ac, les brins 1-cousus à ac n’appartenant pas à ac, b2=bα2, b3=bα3 et b4=b2α3 ; d1=bα10, d2=d1α1, d3=d1α3 et d4=d2α3, et D={d1,d2,d3,d4}. La 3G-carte obtenue en décalant l’arête a le long de l’arête suivant a du coté du sommet incident à b est G′=(B,α0′,α1′,α2′,α3′) définie par :
Cette définition consiste simplement à considérer deux brins supplémentaires par rapport au cas 2D, qui sont les brins d3=d1α3 et d4=d2α3. La première partie de la définition (les points 1, 2 et 3) sont inchangés car la définition est générique. Pour les points 4 et 5, nous ajoutons la définition de α1′ pour ces deux brins supplémentaires, en s’assurant au préalable que nous ne sommes pas dans le cas d’un brin 3-libre (d3=d1 et d4=d2) puisqu’il n’y a alors rien à faire pour ces brins dans ce cas.
Nous montrons Fig. 3.30 un exemple de décalage d’arête 3D dans le cas général, lorsque la face concernée n’est pas 3-libre (autrement nous nous ramenons au cas 2D). Nous voyons bien sur cet exemple que, comme les deux demi-faces concernées par le décalage sont isomorphes, le décalage de l’arête 3D est équivalent à appliquer deux fois l’opération de décalage 2D, une fois par demi-face. De ce fait, les différents cas particulier présentés en 2D vont fonctionner de manière identique en 3D, et nous ne les détaillons pas à nouveau.
[a][b]
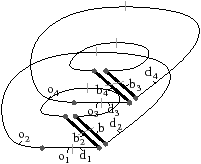
Figure 3.30: Le cas général de décalage d’arête en 3D. (a) La configuration initiale. L’arête c1(b) est à décaler. Les brins d1, d2, d3 et d4 donnent la position où l’arête va être décalée. Les brins o1, o2, o3 et o4 sont les voisins de l’arête qui vont être modifiés : BV={o1,o2,o3,o4}. (b) La G-carte obtenue après le décalage.
Dans ce chapitre, nous avons défini les quatre opérations de base permettant soit de simplifier une subdivision (pour la suppression et la contraction), soit à l’inverse de la raffiner (pour l’insertion et l’éclatement). Ces opérations sont définies de manière générique en dimension quelconque. Les seules contraintes sont celles nécessaires pour garantir que le résultat de l’opération soit bien une G-carte. Nous avons montré que ces opérations permettent de représenter les opérateurs d’Euler en 2D. Comme il a été prouvé que ces opérateurs sont complets (c’est-à-dire que n’importe quel polyèdre 2D peut être construit par une séquence finie de ces opérateurs), cela montre également que nos opérations sont complètes pour les 2G-cartes. Il serait intéressant d’étendre cette preuve aux dimensions supérieures, en montrant toute nG-carte peut être obtenue à partir de n’importe quelle nG-carte par une suite finie d’opérations de base.
Les quatre opérations définies dans ce chapitre peuvent être utilisées comme briques de base dans de nombreuses autres opérations et dans différents cadres. Il sera alors parfois nécessaire de rajouter des contraintes spécifiques, mais les opérations pourront s’appliquer sans aucune modification. Enfin, nous avons défini ces opérations sur les cartes généralisées afin de profiter de leur homogénéité, mais ces définitions se transcrivent pour les cartes combinatoires en utilisant les algorithmes de conversion présentés au chapitre 2.
Nous avons également défini l’opération de décalage d’arête permettant de modifier un sommet dans l’objectif de le rendre supprimable, tout en préservant les autres cellules et relations d’incidence. Contrairement aux quatre opérations précédentes, cette opération est définie dans un cas particulier (uniquement pour les arêtes) et seulement en 2D et 3D. Nous avons commencé à étudier l’extension de cette opération à d’autres types de cellules (par exemple pour décaler les faces) et en toute dimension, mais ce travail n’a pas encore totalement abouti. De plus, nous souhaitons également étudier l’opération duale qui permettrait de rendre possible la contraction d’une cellule en diminuant son co-degré.
Pour toutes ces opérations, il est assez simple de déduire l’algorithme correspondant à la définition. Nous ne l’avons pas fait dans ce chapitre afin de ne pas l’alourdir, mais certains de algorithmes ont été détaillés dans les références suivantes [Dam01, DBF04, Dam08], dans le cadre des cartes combinatoires. De plus, tout ces algorithmes sont locaux car les seules modifications concernent les brins voisins des cellules concernées. De ce fait, la complexité de ces algorithmes est à chaque fois linéaire en nombre de brins des cellules.
Nous verrons dans la suite de ce manuscrit que ces opérations sont au cœur de nos travaux et sont abondamment utilisés dans différents cadres comme par exemple le calcul d’une carte minimale représentant une image étiquetée, la segmentation d’images, ou le calcul de groupes d’homologie.
Nous souhaitons maintenant pouvoir étendre les deux généralisations présentées dans ce chapitre afin de fournir des opérations permettant encore plus d’opérations différentes de manière simultanée. Il est par exemple souhaitable de pouvoir supprimer en une seule fois une arête et le sommet incident à cette arête qui était de degré trois, mais devient de degré deux après la suppression de l’arête. Ce type d’opération est intéressant au niveau de la complexité de l’opération car elle évite plusieurs itérations, mais elle est surtout intéressante dans le cadre des pyramides de cartes, que nous allons présenter au chapitre 5, pour éviter la création de nombreux niveaux intermédiaires inutiles.
Nous allons maintenant nous intéresser à l’utilisation des cartes pour représenter des images 2D/3D. Nous allons voir que la définition du modèle, mais également les opérations que nous allons mettre en place s’appuient sur les opérations de base que nous venons de définir.
Dans ce chapitre, nous nous intéressons aux particularités des cartes combinatoires lorsqu’elles sont utilisées pour représenter des images. En effet, de par la structure régulière des grilles considérées, la topologie des partitions représentées possède des propriétés particulières.
La problématique sous-jacente est la représentation et la manipulation de régions dans une image étiquetée. En effet, la plupart des algorithmes de segmentation ont besoin de représenter le résultat de la segmentation dans une structure de données afin de pouvoir manipuler les régions obtenues, par exemple pour calculer des caractéristiques sur ces régions. Ces caractéristiques peuvent être colorimétriques (par exemple la moyenne des niveaux de gris de la région), géométriques (par exemple une estimation de la forme de la région) ou topologiques (par exemple retrouver toutes les régions adjacentes à une région).
Plusieurs travaux portant sur la définition d’une telle structure de données ont conclu qu’il était intéressant de représenter les subdivisions des régions en cellules, et de décrire les relations d’incidence et d’adjacence entre ces cellules, pour pouvoir ensuite utiliser ces informations au sein d’algorithmes de traitement d’images. C’est dans ce cadre que des recherches ont débuté à la fin des années 1980 sur l’utilisation des cartes combinatoires pour représenter des images 2D [BG88]. Ces travaux se sont ensuite développés dans les années 1990 [Fio96, BD99] notamment durant les trois thèses de Jean-Philippe Domenger [Dom92], Christophe Fiorio [Fio95] et Luc Brun [Bru96]. Les cartes combinatoires 2D ont été aussi utilisées dans des problématiques d’édition d’images [BG89, GHPVT89, BG91] et de segmentation d’images [BDB97, BD97, BB98, AFG99, Köt02, BDM03].
Mais il n’existait pas, lorsque j’ai débuté ma thèse, de travaux en dimension supérieure, et j’ai donc travaillé à la définition d’un modèle combinatoire de représentation d’une image 3D étiquetée et à son utilisation au sein d’opérations de traitement d’images. Pour atteindre cet objectif, j’ai commencé par étudier le problème en 2D car l’extension des modèles existants était délicate. C’est ce travail qui m’a amené à la définition des cartes topologiques en 2D et 3D puis à l’étude d’opérations sur ce modèle.
La principale difficulté, que nous allons retrouver tout au long de ce chapitre, est la propriété de minimalité des cartes manipulées (en nombre de cellules). Cette propriété supplémentaire est liée aux informations sur les régions que nous souhaitons décrire. Intuitivement, lorsque deux régions sont adjacentes, elles se touchent par une zone de contact qui doit être représentée par une seule cellule dans la carte. Cette notion de zone de contact est formalisée dans ce chapitre par la notion d’arête frontière en 2D et de face frontière en 3D. Une seconde difficulté concerne les problèmes de déconnexion susceptibles de se poser durant les simplifications. Ces problèmes doivent être résolus pour garantir l’absence de perte d’information durant les simplifications. Ce sont ces deux problèmes, qui sont d’ailleurs liés, qui rendent difficile la définition des cartes topologiques et qui étaient bloquants dans l’extension des modèles existants en 3D. Dans les deux cas, l’utilisation et le contrôle des opérations de suppression nous à permis de résoudre les problèmes.
Le plan de ce chapitre est le suivant. Tout d’abord nous commençons par présenter Section 4.1 les notions préliminaires liées à la géométrie et topologie discrètes, et nécessaires par la suite. Puis nous présentons Section 4.2 les modèles qui existaient avant que nous démarrions nos travaux. Enfin nous présentons la définition de notre modèle, la carte topologique, tout d’abord en 2D Section 4.3 puis en 3D Section 4.4. Nous présentons à la Section 4.5 les opérations d’extraction, de fusion et de découpe définies sur les cartes topologiques, avant de conclure Section 4.6 et de donner des perspectives de recherche à ce chapitre.
Nous présentons dans cette section les notions de base utiles dans la suite de ce chapitre. Un pixel (resp. voxel) est un point du plan discret ℤ2 (resp. de l’espace discret ℤ3) avec une valeur qui peut être une couleur ou un niveau de gris, et une image de dimension 2 (resp. dimension 3) est un ensemble fini de pixels (resp. voxels). Une image étiquetée est une image dans laquelle chaque pixel (resp. voxel) est étiqueté. Il n’y a pas de contrainte sur cet étiquetage, et il est facile d’associer à n’importe quelle image une image étiquetée simplement en prenant comme étiquette la valeur associée à chaque pixel (resp. voxel).
La distance l1 entre deux points p=(p1,…,pn) et q=(q1,…,qn) d’un espace euclidien est l1(p,q)=∑i=1n|pi−qi|. La distance l∞ est l∞(p,q)=maxi=1n|pi−qi|.
Deux pixels sont 4-adjacents si la distance l1 entre les deux pixels égale à un, ils sont 8-adjacents si la distance l∞ est égale à un. Deux voxels sont 6-adjacents si la distance l1 entre les deux voxels est égale à un, 26-adjacents si la distance l∞ est égale à un, et 18-adjacents s’ils sont 26-adjacents et si la distance l1 est inférieure ou égale à deux. Soit un pixel (resp. voxel) p, son α-voisinage est l’ensemble des pixels (resp. voxels) α-adjacents à p. Nous utilisons l’ordre lexicographique1 pour comparer deux pixels (resp. voxels).
Un α-chemin de pixels (resp. voxels) est une suite de pixels (resp. voxels) deux à deux α-adjacents. Une α-courbe est un α-chemin tel que chaque pixel (resp. voxel) de la courbe, sauf ses deux extrémités, a exactement deux points α-adjacents dans la courbe, les deux extrémités de la courbe ayant exactement un point α-adjacent dans la courbe. Une α-courbe est fermée si c’est un α-chemin tel que chaque pixel (resp. voxel) de la courbe a exactement deux points α-adjacents dans la courbe.
Soit E un ensemble de pixels (resp. voxels). Le complémentaire de E, noté E, est l’ensemble des pixels (resp. voxels) de ℤ2 (resp. ℤ3) n’appartenant pas à E. E est un ensemble α-connexe s’il existe un α-chemin entre chaque couple de pixels (resp. voxels) ayant tous ses éléments dans E.
Dans ce travail, nous choisissons de manipuler les ensembles de pixels 4-connexes (resp. voxels 6-connexes). Cela nous amène à la définition centrale de la notion de région.
Pour éviter un traitement particulier des pixels (resp. voxels) du bord de l’image, nous considérons que l’image est imbriquée dans une région infinie R0 contenant l’ensemble des pixels (resp. voxels) du complémentaire de l’image. Par définition, l’ensemble des régions est une partition des pixels (resp. voxels) de l’image car chaque pixel (resp. voxel) appartient exactement à une seule région de l’image.
La notion d’adjacence est étendue aux régions : deux régions A et B sont α-adjacentes s’il existe un pixel a ∈ A (resp. voxel) et un pixel b ∈ B (resp. voxel) tel que a et b soient α-adjacents. Avec cette notion d’adjacence entre les régions, les notions de α-chemin et de composante α-connexe s’étendent directement aux régions. De plus, l’ordre lexicographique sur les pixels (resp. voxels) s’étend également directement aux régions en utilisant l’ordre sur le plus petit élément de chaque région.
[a][b]

Figure 4.1: Exemple de paradoxes topologiques arrivant lorsque la connexité considérée est la même pour l’objet et pour son complémentaire. (a) Une 8-courbe fermée en gris dont le complémentaire est une seule composante 8-connexe. (b) Une 4-courbe fermée en gris dont le complémentaire est formée de trois composantes 4-connexes : l’extérieur et «deux intérieurs» : la première composante 4-connexe intérieure est composée du pixel 1 et la seconde est composée du pixel 2.
De nombreux travaux ont porté sur l’étude des problèmes topologiques dans un espace discret [HW83, Kov84, KR89, Kov89, KKM90a, KKM91, KU92]. En effet, l’utilisation d’une même relation d’adjacence pour un objet et son complémentaire entraîne des paradoxes topologiques, comme ceux présentés en 2D sur la Fig. 4.1. Ces problèmes sont liés au théorème de Jordan qui dit que dans ℝ2 le complémentaire de toute courbe fermée simple est formée exactement de deux composantes connexes distinctes : un extérieur et un intérieur. Ce théorème est l’un des piliers de la topologie du plan. Dans le plan, toute courbe de Jordan est homéomorphe au cercle unité S2. Dans ℝ3, la notion équivalente est celle de surface de Jordan qui est une surface fermée simple.
La résolution des problèmes topologiques dans un espace discret se fait en considérant une connexité différente pour l’objet et pour son complémentaire [Udu94, Kon02, EL03]. En 2D, le couple de connexité choisi (α, β) doit être tel que chaque α-courbe fermée doit séparer ℤ2 en deux composantes β-connexes. Un tel couple de connexité est appelé paire de Jordan. C’est le cas par exemple des couples (4,8) ou (8,4). En 3D, les couples de connexités à utiliser sont par exemple (6,18) et (6,26).
L’utilisation de ces couples de connexité va également intervenir dans la définition de la relation d’imbrication entre régions. Intuitivement, une région Ri est dite imbriquée2 dans une autre région Rj si Rj «entoure» complètement Ri. Cette notion est une relation topologique liée à la notion d’intérieur et d’extérieur du théorème de Jordan. De ce fait, comme les régions sont définies avec une seule connexité (4 en 2D, 6 en 3D), la connexité possible pour le complémentaire est limitée à 8 en 2D et 18 ou 26 en 3D.
Sur l’exemple de la Fig. 4.1, la région 3, composée des pixels noirs, n’est pas imbriquée dans la région 2 (la région gris clair) car il existe un 8-chemin entre un pixel de la région 3 et un pixel de la région infinie ne passant pas par la région 2. De ce fait, la région 3 est adjacente à une autre région que 2 appartenant à l’extérieur de 2 (même si dans ce cas cette zone de contact est limitée à un point). En 3D, le chemin doit être 18-connexe (et non 26-connexe) à cause de la propriété de quasi-variété des cartes combinatoires (cf. Def. 5 page ??). En effet, deux volumes d’une carte sont nécessairement adjacents par une face. Lorsque deux voxels sont 18-adjacents mais pas 6-adjacents, il y a une seule arête entre les voxels car le volume complémentaire est adjacent à ces deux voxels par deux faces qui sont voisines. Par contre, lorsque deux voxels sont 26-adjacents mais pas 18-adjacents, comme c’est le cas pour le voxel de la région 3 et le voxel de la région 1 dans la Fig. 4.1, les deux voxels ne partagent pas de sommet commun car les volumes ne partagent ni face, ni arête commune. De ce fait, les frontières des régions 1 et 3 de l’exemple sont disjointes et la région 3 touche uniquement la région 2 : la région 3 est donc imbriquée dans la région 2 ce qui fait que la seule connexité possible pour le complémentaire est la 18-connexité.
[a][b]
[c]
Figure 4.2: Exemples de relation d’imbrication et de relation d’imbrication directe. (a) La région 3 (pixels noirs) n’est pas imbriquée dans la région 2 (pixels gris clair) car elle est 8-adjacente à la région 1. (b) La région 3 (voxels noirs) est imbriquée dans la région 2 (voxels gris clair) car chaque 18-chemin entre la région 3 et la région infinie traverse la région 2. (c) La région 4 est directement imbriquée dans la région 1 bien que les régions ne soient pas adjacentes, car les trois régions 2, 3 et 4 appartiennent à la même composante 8-connexe imbriquée dans 1.
Il est simple de prouver que la relation d’imbrication est une relation d’ordre. Il est souvent suffisant de s’intéresser à la réduction transitive de la relation d’ordre afin de s’intéresser à la plus petite région contenant une région donnée : c’est la relation d’imbrication directe. Chaque région Ri (à l’exception de la région infinie) est directement imbriquée dans exactement une région Rj, Ri et Rj n’étant pas nécessairement adjacentes (cf. l’exemple de la Fig. 4.1). Par contre, chaque région possède entre 0 et k régions directement imbriquées. Dans la suite de ce manuscrit, nous utiliserons toujours la relation d’imbrication directe que nous appellerons imbrication pour simplifier.
De nombreux travaux ont porté sur la représentation des contours dans une image discrète [Kov89, KR89, KKM90b, KKM91, Fio95]. Ces travaux utilisent tous la notion de topologie interpixel en 2D ou intervoxel en 3D. Le principe intuitif de ces topologies est de ne pas considérer uniquement les éléments de l’image mais également tous les éléments de dimension inférieure séparant ces éléments. Par exemple en 2D, les pixels (éléments unitaires 2D) sont séparés par des lignels (éléments unitaires 1D), eux-mêmes séparés par des pointels (éléments unitaires 0D). En 3D, le principe est similaire en considérant les voxels (éléments unitaires 3D), surfels (éléments unitaires 2D), lignels et pointels (cf. exemple Fig. 4.3). Plus formellement, la notion de complexe cellulaire3 ℂn [Kov89] est la décomposition cellulaire de l’espace euclidien ℝn en grille régulière. Les notions d’adjacence et d’incidence se retrouvent dans ℂn directement à partir des notions de bord existantes dans ℝn. ℂin est l’ensemble des i-cellules de la décomposition cellulaire, et donc ℂn=∪i=0n ℂin.
Une autre manière d’introduire l’interpixel/intervoxel [KKM90b] est l’utilisation de la topologie produit. Tout d’abord, la topologie sur ℤ est définie en prenant tous les nombres pairs comme des fermés, et les nombres impairs comme des ouverts. Intuitivement, les fermés sont les pointels et les ouverts les lignels. Cette topologie est appelée topologie de Khalimsky ou topologie digitale. Elle s’étend ensuite directement en dimension n en effectuant le produit de n topologies de Khalimsky 1D (cf. l’exemple en 2D donné Fig. 4.4). Les ouverts sont les points ayant des coordonnées toutes impaires, et les fermés les points ayant des coordonnées toutes paires. Les autres points ayant les deux types de coordonnées sont des points mixtes. Il a été prouvé dans [KKM90b, KKM91] que la topologie de Khalimsky est équivalente à la topologie des complexes cellulaires. De plus, le lien entre les inter-éléments et la topologie produit de n ensembles d’entiers fournit un codage simple des inter-éléments [Lac03, KR04].
En 2D, la topologie de Khalimsky est donc la topologie produit ℤ × ℤ, où les ouverts sont les pixels, les fermés les pointels, et les lignels des points mixtes. En 3D, c’est ℤ × ℤ × ℤ avec les voxels étant les ouverts, les pointels les fermés, et les lignels et les surfels des points mixtes. Avec ces notations, deux inter-éléments sont incidents si la différence deux à deux entre chaque coordonnée est au plus un, et ils sont adjacents s’ils ont toutes leurs coordonnées égales sauf une, et si la différence pour cette coordonnée est deux (intuitivement les deux inter-éléments sont séparés par un inter-élément ce qui explique la différence de deux).
Il est possible de définir la notion de chemin et de connexité pour un ensemble d’inter-éléments de même dimension, de manière similaire aux définitions pour les pixels et voxels. Nous utilisons par exemple un chemin de surfels qui est défini par une suite de surfels (s1, …, sk) tel que chaque couple de surfels consécutifs si, si+1 soient adjacents.
Comme nous voyons dans la Def. 61 (que l’on peut trouver par exemple dans [Her98, Kov08]), un des avantages des approches inter-éléments est de pouvoir définir la frontière entre deux régions par un ensemble d’éléments entre les pixels (ou voxels) de la région et non pas par un ensemble de pixels (ou voxels) ce qui pose des problèmes de non-symétrie. En effet, les pixels (ou voxels) de la frontière entre deux régions A et B sont pris soit dans la région A, soit dans la région B. Rendre cette notion de frontière symétrique est possible en prenant à la fois les pixels (ou voxels) dans A et dans B, mais cela pose alors un autre problème qui est que la frontière n’est plus mince (c-à-d les éléments de la frontière ne sont plus voisins d’éléments appartenant à A et à B). Un autre avantage de la définition des frontières inter-éléments est de permettre la définition de l’analogue du théorème de Jordan dans le cas discret. Cela permet de prouver que toute frontière sépare l’espace discret en deux composantes connexes.
Ce type d’approche a été utilisé afin de définir les surfaces en intervoxels [Her98, Kov08]. Il faut noter que l’approche [Her98] n’utilise pas directement une approche inter-éléments mais utilise une approche à base de graphe, où les sommets du graphe correspondent aux voxels et les arêtes représentent la relation d’adjacence utilisée (par exemple la 6-adjacence). En pratique, si l’adjacence utilisée est la 6-adjacence, ce graphe peut être vu comme une représentation intervoxel ou chaque arête correspond à un surfel, et les deux approches sont alors équivalentes.
La Def. 61 introduit la définition de frontière d’une région en 2D et 3D en utilisant un espace interpixels/intervoxels.
Dans [Her98, Kov08], il est prouvé que ces frontières ont des «bonnes» propriétés lorsque le couple de connexité considéré est une paire de Jordan (ce qui est notre cas). En 2D, chaque composante connexe de la frontière est courbe de Jordan. En 3D, chaque composante connexe de la frontière est une surface presque-Jordan, c’est-à-dire qu’elle sépare l’espace en deux parties disjointes : un intérieur et un extérieur. Le terme presque-Jordan (défini dans [Her98]) est employé car ces surfaces discrètes séparent bien l’espace en deux composantes connexes, comme les surfaces de Jordan dans l’espace euclidien, mais ce ne sont pas forcément des 2-variétés (cf. exemple Fig. 4.5).
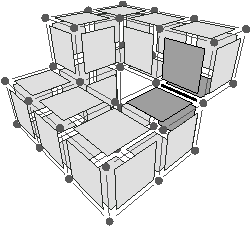
Figure 4.5: Exemple de surface presque-Jordan qui n’est pas une 2-variété. Le voisinage du lignel noir et épais est composé des quatre surfels en gris foncé et n’est pas homéomorphe à une 2-boule ouverte.
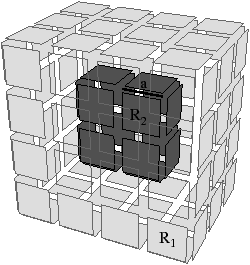
Figure 4.6: Exemple de frontière non-connexe. La frontière de R1 est composée de deux composante connexes de surfels car R1 possède une cavité.
Il faut noter que la frontière d’une région n’est pas forcément connexe, lorsqu’une région possède des cavités (cf. exemple Fig. 4.6). Dans ce cas, chaque frontière sépare la région et une composante connexe de son complémentaire. Pour pouvoir désigner plus précisément certaines parties de la frontière d’une région, nous la décomposons en sous-parties en introduisant les notions suivantes :
La notion d’arête/de face frontière (cf. Def. 62) est importante car nous souhaitons représenter la multi-adjacence inter-régions. Il faut donc savoir combien de fois deux régions se touchent et pour cela être capable d’identifier précisément une zone maximale de contact.
De manière intuitive, une arête/face frontière est un ensemble maximal et connexe d’éléments séparant les deux régions A et B, tel qu’il existe un chemin reliant tout couple d’éléments de cet ensemble. C’est l’existence ou non de ce chemin qui fait que deux éléments séparant A et B appartiennent à la même zone de contact ou pas.
La notion de surface frontière (cf. Def. 63) est quant à elle nécessaire pour traiter correctement le cas des régions ayant des cavités.
En 2D, chaque région R possède toujours une courbe frontière dite externe telle que l’intérieur de cette courbe contiennent tout les pixels de R, et entre 0 et k contours internes, un par cavité de R. Il en est de même en 3D pour la surface frontière externe et les éventuelles surfaces frontières internes. La frontière entre deux régions peut être vide lorsque les régions ne sont pas adjacentes, elle peut être composée d’une seule arête/face frontière lorsque les deux régions sont simplement adjacentes, ou de plusieurs arêtes/faces frontières lorsque les régions sont multi-adjacentes.
Il est facile de prouver que les arêtes (resp. faces) frontières forment une partition des courbes (resp. surfaces) frontières c’est-à-dire qu’une courbe (resp. surface) frontière est une union d’arêtes (resp. de faces) frontières, et que l’intersection de deux arêtes (resp. faces) frontières différentes est toujours vide. De même, les courbes (resp. surfaces) frontières forment une partition des frontières. De ce fait, la frontière d’une région R est l’union de toutes ses arêtes (resp. faces) frontières avec toutes les autres régions.
La première structure de données qui a été définie dans l’objectif de représenter une image segmentée est le graphe d’adjacence de régions (appelé RAG) [Ros74]. C’est un graphe associant un sommet à chaque région de l’image, et deux sommets sont reliés par une arête lorsque les deux régions correspondantes sont voisines.
[a][b]
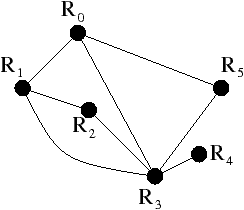
Figure 4.7: Exemple de graphe d’adjacence des régions. (a) Une image 2D segmentée en régions. (b) Le RAG correspondant.
Ce graphe d’adjacence possède comme avantages d’avoir une définition simple et générique quelle que soit la dimension de l’image. Par contre, il possède comme inconvénients majeurs de ne pas représenter les adjacences multiples ni l’ordre entre les régions adjacentes à une même région, de ne pas différencier les relations d’adjacence et les relations d’imbrication, et de ne pas représenter toutes les cellules ni les relations d’incidence. Ces problèmes deviennent majeurs dès la dimension trois où le graphe d’adjacence contient alors très peu d’information topologique.
Pour résoudre ces problèmes, les graphes d’adjacences ont été étendus, tout d’abord de manière directe pour représenter la multi-adjacence, puis pour représenter l’ordre des régions autour d’une région. Pour cela, les graphes duaux ont été définis [WK94, KM95, Kro95].
L’idée principale des graphes duaux est de conserver deux graphes en parallèle, un multi-RAG d’un côté, et son graphe dual de l’autre. Le premier graphe représente les adjacences entre régions, avec des boucles lorsqu’une région contient des régions imbriquées. Ces boucles proviennent du fait que le graphe primal et son dual doivent tous deux être connexes. De ce fait, dans le dual, une arête permet à la région imbriquée d’être reliée à la région qui l’entoure. Cette arête devient, dans le graphe primal, une boucle autour de la région imbriquée.
[a][b]
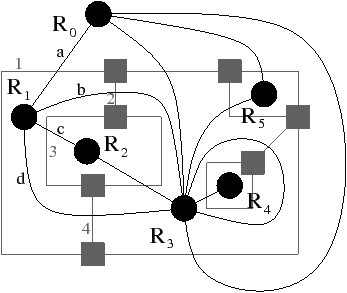
Figure 4.8: Exemple de graphes duaux. (a) Une image 2d segmentée en régions. (b) Les graphes duaux correspondant. En noir le graphe primal (qui est un multi-RAG), et en gris son graphe dual.
En parcourant simultanément les deux graphes, il est possible de retrouver l’ordre des régions adjacentes à une région donnée. Sur l’exemple de la Fig. 4.8, le parcours des régions adjacentes à la région R1 de manière ordonnée se fait en partant d’une arête d’extrémité R1 et de son arête duale, par exemple (a,1). Ensuite, parmi les arêtes d’extrémité R1 (b, c et d), il en existe seulement deux ayant leur arête duale adjacente à l’arête 1. Ces deux arêtes sont les deux orientations possibles pour tourner autour de la région R1. Nous choisissons un couple, par exemple (b,2) et continuons le parcours en prenant parmi les arêtes incidentes à R1 celle telle que son arête duale soit adjacente à l’arête 2. Il y a encore deux possibilités, mais une des deux est l’arête précédente du parcours. Nous choisissons donc l’autre qui est (c,3). La dernière arête obtenue est (d,4) avant de revenir sur l’arête initiale (a,1).
Les graphes duaux résolvent certains problèmes du RAG. En effet, leurs principaux avantages sont qu’ils :
Mais il reste des inconvénients :
C’est pour répondre à ces problèmes que les travaux cherchant à utiliser les cartes combinatoires pour représenter des images se sont développés. En effet, une carte combinatoire 2D code explicitement l’ordre des arêtes autour des sommets, et représente toutes les cellules de la subdivision (sommets, arêtes et faces). Le principe des deux approches principales développées durant les thèses de Jean-Philippe Domenger, Luc Brun et Christophe Fiorio est d’utiliser une carte combinatoire pour représenter les frontières interpixels des régions de l’image. Les deux approches sont similaires sur la définition de la carte combinatoire utilisée, mais diffèrent pour le codage de la carte, le codage de la relation d’imbrication et pour l’algorithme calculant le modèle à partir de l’image.
Le premier modèle, appelé carte discrète, a été développé initialement durant la thèse de Jean-Philippe Domenger puis durant la thèse de Luc Brun (cf. exemple Fig. 4.2.3). Ce modèle utilise une carte combinatoire M=(B,α,σ) dans laquelle chaque arête correspond à une arête frontière entre deux régions de l’image, et chaque sommet correspond soit à l’intersection de plus de deux arêtes frontières (donc 3 ou 4 frontières vu que l’espace sous-jacent est discret), soit à un sommet arbitraire de l’arête frontière dans le cas d’une arête frontière fermée (cas de la frontière entre les régions R3 et R4 sur l’exemple). Chaque face (c’est-à-dire une orbite ⟨ϕ⟩) est identifiée par une étiquette, et λ donne pour chaque brin l’étiquette de sa face (ces faces sont numérotées de f1 à f7 sur l’exemple de la Fig. 4.2.3). La face représentant l’extérieur de la carte combinatoire est appelée face infinie (la face f1 de l’exemple) tandis que les autres faces sont appelées faces finies. Par convention, les brins sont numérotés de telle manière que pour chaque brin b de numéro i, le brin α(b) soit numéroté −i. Cette convention permet, lorsque les brins sont représentés dans un tableau, de ne pas avoir besoin de représenter explicitement l’involution α. Par contre, cela complexifie les mises à jour lorsqu’il faut modifier cette involution, car cela nécessite de réorganiser les brins au sein du tableau.
[a][b]
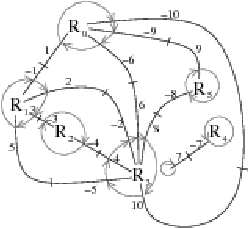
Figure 4.9: (a) La carte discrète et (b) le graphe topologique des frontières de l’image de la Fig. 4.2.2. Les brins des deux modèles sont numérotés de manière identique pour faciliter la comparaison.
De par sa définition, lorsqu’une région est imbriquée dans une autre région (comme la région R4 dans l’exemple de la Fig. 4.2.3), la carte combinatoire n’est pas connexe. En effet, il n’y a pas d’arête frontière reliant les deux courbes frontières représentant l’extérieur de la face et la cavité. Dans ce cas, la carte est composée d’un ensemble de composantes connexes, chacune ayant une face infinie (sur l’exemple de la Fig. 4.2.3, il y a deux composantes connexes donc deux faces infinies f1 et f6). Il n’existe pas de relation dans la carte combinatoire entre les différentes composantes connexes4. Pour résoudre ce problème, les relations d’imbrication sont représentées à l’aide de deux fonctions sur les étiquettes des faces : Parent et Children. La fonction Parent associe à chaque face infinie l’étiquette de la face finie la contenant (à l’exception de la face infinie englobant l’image qui n’est contenue dans aucune face). La fonction Children associe à chaque face finie l’ensemble des étiquettes des faces infinies imbriquées dans la face (par exemple Parent(f6)=f4 et Children(f4)={f6}). Ces deux fonctions permettent de parcourir l’ensemble des courbes frontières d’une région donnée, et permettent également de retrouver la région entourant une autre région. Enfin, la géométrie de la carte discrète est codée à l’aide d’une matrice d’éléments interpixels dans laquelle seuls les pointels associés aux sommets, et seuls les lignels appartenant aux frontières sont allumés. Chaque brin est associé avec un couple (pointel, lignel) donnant le point de départ et la direction initiale de l’arête frontière. À partir de ce point de départ, il est simple de parcourir tous les lignels de l’arête frontière en suivant les lignels allumés jusqu’à trouver un pointel allumé indiquant la fin de l’arête frontière.
Les cartes discrètes ont été ensuite étendues en 3D [BDDW99, BDD01, Des01, BDDV03] en utilisant un principe similaire à la solution proposée en 2D. Les principaux changements sont l’utilisation d’une carte combinatoire 3D codée par une matrice d’éléments intervoxels, et représentant les régions. Un brin est donc représenté par un triplet (pointel, lignel, surfel), et des fonctions sont définies sur ces triplets pour retrouver directement les différentes relations sur les brins. Mais cette solution n’a pas pu être utilisée en pratique car car la représentation des brins par un triplet n’est possible que pour des images étiquetées dites faiblement bien-composées, c’est à dire dans lesquelles il n’existe pas deux voxels 18-adjacents appartenant à la même région. Cela rend ce modèle peu utilisable en pratique, car il nécessite une étape de normalisation d’une image avant de pouvoir en calculer la carte discrète, étape itérative et donc coûteuse, qui de plus modifie les régions de l’image segmentée. Cela rend également difficile les opérations puisqu’après chaque modification de la carte, il faut vérifier si cela n’a pas entraîné une configuration interdite, et le cas échéant régler le problème, à nouveau de manière itérative. Pour ces raisons, autant l’approche 2D a été utilisée afin de résoudre des problématiques de segmentation d’images [BDB97, BD97, BB98, BDM03], autant le problème lié à l’approche 3D c’est avéré bloquant. De ce fait, les travaux successeurs de cette approche ont consisté à repartir sur un modèle à base de graphe d’adjacence étendu, en le liant avec une matrice d’éléments intervoxels [BBDD08, Bal09, BBD09].
Le second modèle, appelé graphe topologique des frontières (TGF), a été développé durant la thèse de Christophe Fiorio (cf. exemple Fig. 4.2.3). Son principe, très proche de la carte discrète, est toujours d’utiliser une carte combinatoire représentant une arête par arête frontière entre deux régions de l’image. Les différences portent simplement sur :
La carte combinatoire et les régions sont liées car chaque brin connaît sa région d’appartenance. Enfin, une région supplémentaire (la région infinie) est ajoutée qui représente le complémentaire de l’image.
La première différence est anecdotique car les utilisations d’une carte ou de sa duale sont équivalentes. La seconde différence change la manière de parcourir la structure. Ici, la notion de région est maintenant explicitée contrairement aux cartes discrètes. De ce fait, retrouver les courbes frontières internes d’une région se fait ici à l’aide de la liste des brins, ce qui est équivalent à l’utilisation de la fonction Children pour les cartes discrètes. Enfin, une dernière différence entre les deux modèles concerne la manière usuelle de les dessiner, comme nous pouvons le vérifier sur la Fig. 4.9. Pour les cartes discrètes, les arêtes sont dessinées le long des frontières des régions ce qui permet de faire plus facilement le lien avec la géométrie des régions, alors que pour le TGF les arêtes sont dessinées de manière similaire à un RAG ce qui rend son interprétation visuelle plus délicate. Mais la encore, c’est une différence négligeable, d’autant plus que c’est uniquement une habitude et qu’il est possible de dessiner le TGF de manière similaire aux cartes discrètes (comme nous l’avons présenté Section 2.2.2).
Lorsque j’ai débuté ma thèse, l’objectif était d’étendre ces modèles en 3D. Les cartes combinatoires avaient déjà été définies en dimension quelconque, il semblait alors naturel de vouloir poursuivre les travaux autour de la carte discrète ou du TGF afin d’utiliser ces cartes combinatoires pour représenter des images 3D. Mais cette tâche s’est vite avérée très difficile de par la définition directe de ces deux modèles. En effet, le problème en 2D est suffisamment simple pour que nous puissions définir directement la subdivision voulue (principalement une arête par arête frontière) et la carte associée (car une arête est toujours composée de deux brins dans une carte combinatoire 2D fermée). Cela devient beaucoup plus délicat en 3D où il faut définir la notion de surface frontière en intervoxel, mais cette notion n’est plus suffisante car nous devons nous intéresser aux bords de ces surfaces et à la manière dont ils se rejoignent. Les cas possibles deviennent beaucoup plus nombreux et complexes à visualiser. Enfin, le nombre de brins associés aux cellules de la subdivision peut maintenant être quelconque ce qui complexifie encore plus la tâche.
Pour résoudre ce problème, je me suis reposé la question de la définition d’un modèle 2D mais dans l’optique d’avoir une définition pouvant s’étendre directement en dimension supérieure. C’est ce qui m’a amené à définir la carte topologique, qui en 2D est très proche des deux modèles qui existaient déjà, mais dont l’avantage principal est sa définition progressive basée sur la notion nouvelle de niveaux de simplification. Ces niveaux facilitent la définition du modèle, sont directement extensibles en dimension supérieure, fournissent directement un algorithme de construction et enfin facilitent l’étude des propriétés. En effet, un niveau de simplification s’obtient à partir du niveau précédent par application d’un seul type d’opération, ce qui simplifie l’étude des propriétés en diminuant le nombre de cas à considérer. Une version préliminaire de ces travaux a été présentée dans [BDF00, BDF01], un résumé dans [DB07], et les versions complètes ont été publiées en 2D dans [DBF04] et en 3D dans [Dam08].
Pour définir la carte topologique 2D, c-à-d la carte combinatoire minimale décrivant une image 2D étiquetée, nous avons défini la notion de niveaux de simplification. Le principe général de ces niveaux de simplification consiste à donner une suite de définitions constructive de chaque niveau à partir du niveau précédent. Chaque niveau s’obtient à partir du niveau précédent par application d’un ensemble d’opérations de suppression de même type. Définir la carte topologique revient donc à définir le niveau initial, puis les propriétés des cellules à supprimer pour chaque nouveau niveau.
Pour décrire une image étiquetée, la carte initiale va représenter chaque élément interpixel de l’image, le premier niveau va supprimer les arêtes séparant deux pixels de même étiquette, et le dernier niveau va supprimer les sommets se trouvant au milieu d’une arête frontière. Ces niveaux sont définis plus formellement par les Defs. 64, 65 et 66.
La carte combinatoire initiale C=(B,β1,β2), appelée niveau 0, représente chaque élément interpixel de l’image (cf. Fig. 4.10). Cette carte contient (n × m)+1 faces, et ne représente pas les frontières des régions mais tous les éléments de l’image.
[a][b]
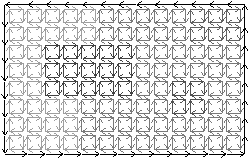
Figure 4.10: Le niveau 0 d’une image 2D. (a) Une image étiquetée. (b) La carte de niveau 0 correspondante.
La carte de niveau 1 s’obtient en supprimant toute les arêtes séparant deux pixels de même étiquette (cf. Fig. 4.11). Après ces suppressions, les seules arêtes restantes séparent deux régions distinctes : cette carte représente donc les frontières interpixels des régions de l’image. C’est uniquement lors de la construction de ce niveau que les données de l’image sont prises en compte afin de décrire les régions de l’image.
[a][b]
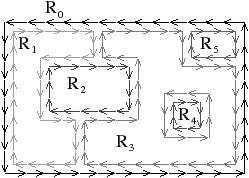
Figure 4.11: La carte de niveau 1 d’une image. (a) Le niveau 0. (b) La carte de niveau 1 correspondante.
La dernière étape de simplification utilise uniquement la carte combinatoire et les propriétés des cellules.
La carte de niveau 2 s’obtient en supprimant successivement tous les sommets supprimables et de degré deux de la carte du niveau précédent (cf. Fig. 4.12). En effet, ces sommets appartiennent nécessairement au milieu d’une même arête frontière puisque, comme nous l’avons vu lors de la présentation des modèles existants Section 4.2.3, les sommets extrémités de ces frontières sont nécessairement soit incidents à une boucle (donc de degré un), soit de degré trois ou quatre.
[a][b]
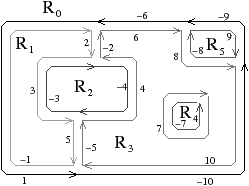
Figure 4.12: La carte de niveau 2 d’une image. (a) Le niveau 1. (b) La carte de niveau 2 correspondante. La numérotation des brins utilisée ici est la même que pour la Fig. 4.9 pour faciliter la comparaison.
Dans cette définition, il est nécessaire d’utiliser les deux conditions supprimable et de degré deux, pour résoudre correctement le cas des boucles (dans le cas général, si le sommet est incident à deux arêtes distinctes, il est de degré deux et supprimable). Deux cas peuvent se produire. Premièrement, lorsque deux boucles sont incidentes au même sommet (cf. Fig. 4.3.2), le sommet est de degré deux (incident à exactement deux arêtes distinctes), mais il n’est pas supprimable. Le second cas est celui d’un sommet de degré un (cf. Fig. 4.3.2). Ce type de sommet est supprimable mais ne doit pas l’être sous peine de faire disparaître totalement l’arête frontière associée à la boucle (l’arête frontière entre R1 et R2 sur l’exemple). Il n’y a pas d’autre cas à considérer que ces deux cas de par les propriétés de l’espace discret sous-jacent qui rend impossible plus de deux boucles autour d’un même sommet.
[a][b]
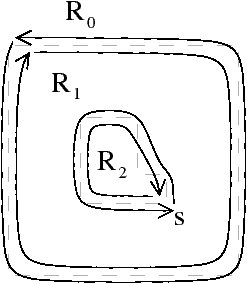
Figure 4.13: Cas pour lesquels la Def. 66 utilise les deux conditions : sommets supprimables et de degré deux. (a) Le cas d’un sommet s de degré deux qui ne doit pas être supprimé car il n’est pas supprimable. (b) Le cas d’un sommet s supprimable qui ne doit pas être supprimé car il n’est pas de degré deux.
Il faut noter le terme successivement qui est nécessaire pour traiter correctement le cas des arêtes frontières fermées (comme la frontière entre R3 et R4 dans l’exemple). En effet, tous les sommets de ce type de frontière sont initialement supprimables et de degré deux. Si les suppressions se font de manière simultanée, tous ces sommets vont être supprimés et l’arête frontière va disparaître. Par contre, en effectuant les suppressions de manière successive, le dernier sommet considéré sera alors de degré un puisqu’il ne restera plus qu’une seule arête : de ce fait il sera conservé. Il faut noter que la position de ce sommet dépend de l’ordre de suppression des sommets, mais ce n’est pas important car topologiquement toutes les configurations obtenues sont équivalentes.
Cette carte de niveau 2 est équivalente aux deux modèles qui existaient au préalable (la carte discrète et le graphe topologique des frontières). La carte utilisée est la même que celle du TGF : la permutation relie les arêtes frontières successives d’une même courbe frontière contrairement à la carte discrète qui est la carte duale. Comme dans ces deux modèles, nous devons rajouter des informations afin de représenter les relations d’imbrication. Nous avons choisi de les représenter par un arbre d’imbrication des régions contenant chaque région de l’image. Pour lier les deux structures de données, chaque brin b connaît sa région d’appartenance, notée region(b), et chaque région connaît un de ses brins (qui doit vérifier des propriétés spécifiques comme expliqué ci-dessous).
La racine de l’arbre d’imbrication est toujours la région infinie. Chaque région R connaît la région dans laquelle elle est directement imbriquée (notée father(R)). À l’inverse, chaque région R connaît les régions qui sont directement imbriquées dans R. Pour avoir un accès direct aux cavités de R, ces régions sont regroupées par composantes 8-connexe. En effet, chaque composante 8-connexe de régions directement imbriquée dans R représente une même cavité (cf. exemple Fig. 4.14). Cette définition respecte la contrainte, déjà évoquée plus haut, que la connexité de l’objet doit être différente de la connexité du fond [KR89]. Dans notre cas, l’objet est la région considérée R qui est 4-connexe par définition, et le fond est l’union de toute les autres régions qui est donc considérée avec la 8-connexité. De ce fait, une région R a pour fils l’ensemble des plus petites régions (au sens lexicographique) de chaque composante 8-connexe de régions imbriquées, les autres régions étant accessibles à partir de ces régions par une relation d’appartenance à la même composante connexe.
[a][b]
[c]
Figure 4.14: Exemple d’arbre d’imbrication des régions. (a) Une image 2D étiquetée, ses régions, et ses frontières interpixels. (b) La carte de niveau 2 correspondante. Cette carte est composée de trois composantes connexes car la région R1 possède deux cavités : une première composée des régions {R2,R3} et une seconde des régions {R4,R5,R6}. (c) L’arbre d’imbrication associé. R1 a pour fils R2 et R4 (les plus petites régions de chaque composante 8-connexe de régions imbriquées), les autres régions sont accessibles par la relation sameCC symbolisée par les ensembles pointillés.
Nous identifions un brin particulier de chaque région R appelé brin représentant, noté rep(R). Ce brin représentant doit vérifier la propriété : region(β2(rep(R))<R (la région du brin atteignable par β2 à partir du brin représentant doit être plus petite que la région R). Cette propriété garantit que le brin représentant est situé sur le contour frontière extérieur de la région (car les régions imbriquées dans R sont forcément plus grandes que R dans l’ordre lexicographique). De plus, cela garantit également que pour chaque ensemble 8-connexe de régions, en prenant la plus petite région de cet ensemble A, la région du brin β2(rep(A)) est toujours la région dans laquelle A (et donc toute les régions de la composante 8-connexe) est directement imbriquée.
Dans la carte de la Fig. 4.3.3, le brin représentant de R1 est forcément le brin 1 (car c’est le seul brin de R1 vérifiant la propriété ci-dessus). Le brin représentant de R2 est le brin 2 et celui de R4 est le brin 4. Dans ces trois cas, nous pouvons vérifier que le brin relié par β2 au brin représentant appartient à la région dans laquelle est imbriquée la région du brin (par exemple pour le brin 2 qui appartient à la région R2, β2(2) appartient à la région R1 et R2 est bien imbriquée dans R1).
Une région R est dite isolée lorsque qu’elle est la seule région d’une composante 8-connexe. Une région de ce type est imbriquée dans une région englobante et n’a pas d’autre région adjacente sauf éventuellement des régions imbriquées (formant des cavités et donc n’appartenant pas à la même composante 8-connexe).
L’arbre d’imbrication des régions et les propriétés sur le brin représentant font qu’il est possible de parcourir directement chaque courbe frontière d’une région R donnée : la courbe extérieure est obtenue par l’orbite ⟨β1⟩(rep(R)), et ses éventuelles courbes frontières intérieures s’obtiennent par les orbites ⟨β1⟩(rep(β2(F)) pour chaque fils F de R. De plus, l’ordre des régions et la position du brin représentant se calculent sans surcoût lors du balayage de l’image pour construire la carte [Dam08].
La carte combinatoire de niveau 2 plus l’arbre d’imbrication des régions permet de représenter la topologie de l’image (les régions et les cellules de la subdivision, les relations d’incidence, d’adjacence et d’imbrication). Mais il faut également représenter la géométrie des régions. Pour cela, nous pouvons utiliser la même solution que celle des cartes discrètes, c’est-à-dire utiliser une matrice d’éléments interpixels dans laquelle nous allumons les lignels appartenant à une frontière interpixel et les pointels à l’intersection de plus de deux arêtes frontières (cf. exemple Fig. 4.3.3). Il suffit alors d’associer à chaque brin un couple (pointel, lignel) pour donner le point de départ et la direction de l’arête frontière associée pour être capable de retrouver la géométrie de chaque élément en combinant les informations données par la carte (par exemple pour retrouver toutes les courbes frontières d’une région) et celles données par la matrice.
Nous avons expérimenté d’autres types de représentation de la géométrie [Dam01, DBF04] dans lesquelles nous associons des listes de points 2D à chaque arête orientée (cf. exemple Fig. 4.15), ou une autre variante dans laquelle nous associons également un point 2D à chaque sommet de la carte (cf. exemple Fig. 4.16) ce qui évite de représenter plusieurs fois les points extrémités des arêtes frontières. Il est possible d’envisager d’autres solutions, par exemple en utilisant des cartes généralisées 1D afin de s’affranchir de l’orientation, voire d’associer des ensembles de pixels à chaque région…Chaque méthode a ses propres avantages et inconvénients qui, de manière classique, oscillent entre gain en espace mémoire et gain en temps d’accès aux informations. La représentation par matrice d’éléments interpixel est plus coûteuse en espace mémoire, mais facilite les parcours, par exemple pour parcourir les pixels à l’intérieur d’une région donnée. Les représentations de la géométrie des frontières offrent une représentation plus compacte en mémoire, facilitent les parcours de la géométrie des frontières qui est donnée explicitement, mais rends plus complexe le parcours des pixels des régions qui ne sont pas manipulables directement.
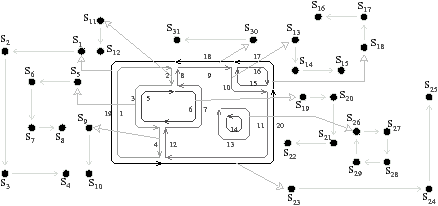
Figure 4.15: Exemple de représentation de la géométrie en associant une liste de points 2D à chaque arête orientée. Les sommets aux extrémités des listes sont dupliqués entre toutes les listes des arêtes incidentes aux mêmes sommets.
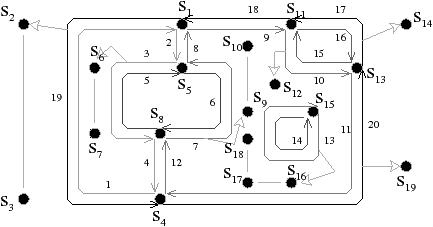
Figure 4.16: Exemple de représentation de la géométrie en associant une liste de points 2D à chaque arête orientée privée de ses extrémités, et un point 2D à chaque sommet. Ces sommets ne sont donc plus dupliqués.
Nous appelons carte topologique le modèle composé de la carte combinatoire de niveau 2, de l’arbre d’imbrication des régions, et d’une représentation de la géométrie. Ce modèle est équivalent aux deux modèles qui existaient déjà au démarrage de mes travaux, mais nous pouvons observer dans les différentes définitions des niveaux les avantages de notre approche par simplifications successives. Les définitions sont simples car progressives. Nous n’avons pas besoin de définir la notion d’arête frontière mais simplement de nous intéresser aux éléments à supprimer (par contre nous utilisons les arêtes frontières pour prouver les propriétés des cartes topologiques). De plus, il est facile d’ajouter des niveaux de simplification intermédiaires comme par exemple dans [DBF04] où nous avions un niveau supplémentaire pour lequel chaque arête correspondait à un ensemble de lignels alignés. Enfin, le principal avantage de ces niveaux de simplification est de s’étendre directement en dimension supérieure.
Afin de définir la carte topologique 3D, nous appliquons le même principe qu’en dimension 2 des niveaux de simplification. Nous commençons par définir une carte combinatoire représentant chaque élément intervoxel de l’image (cf. Fig. 4.17) puis nous la simplifions progressivement.
[a][b]
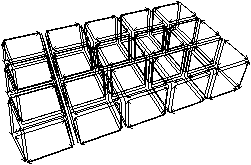
Figure 4.17: Le niveau 0 d’une image 3D. (a) Une image étiquetée. (b) La carte de niveau 0 correspondante (pour des raisons de visibilité, nous ne dessinons pas de manière générale le volume infini).
Le niveau 1 est totalement équivalent au niveau 1 en dimension 2 en remplaçant pixel par voxel : il consiste à fusionner les voxels pour représenter les frontières des régions (cf. Fig. 4.18).
[a][b]
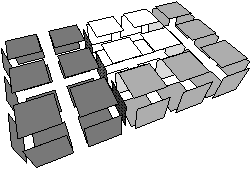
Figure 4.18: Le niveau 1 d’une image 3D. (a) La carte de niveau 1 obtenue à partir de la carte de niveau 0 de la Fig. 4.4. (b) La subdivision correspondante.
Cette carte de niveau 1 représente les frontières de chaque région. En suivant le même principe que pour la dimension 2, nous allons maintenant simplifier cette carte pour représenter chaque relation d’adjacence de manière unique. Le fait d’avoir augmenté l’espace d’une dimension entraîne de manière logique un niveau de simplification supplémentaire : nous allons tout d’abord supprimer des arêtes puis supprimer des sommets. Les suppressions doivent être réalisées par dimensions décroissantes car la suppression d’une i-cellule diminue le degré des (i−1)-cellules. De ce fait, une (i−1)-cellule peut devenir supprimable après la suppression de i-cellules. Traiter les cellules par dimensions décroissantes permet de garantir qu’à la fin du traitement il ne reste plus de cellule supprimable.
Pour définir le niveau 2, nous devons supprimer deux types d’arêtes : les arêtes supprimables et de degré deux (de manière similaire au cas de la dimension 2) et les arêtes pendantes.
Nous devons utiliser les deux conditions supprimable et de degré deux, pour les mêmes raisons qu’en 2D : le cas d’une arête entre deux faces repliées sur l’arête (cf. Fig. 4.4.2), et le cas d’une région isolée (cf. Fig. 4.4.2). Dans le premier exemple, l’arête incidente à R2 et à R3 est conservée car elle est de degré deux mais non supprimable. Dans le second exemple, la dernière arête de la face de R2 est conservée car elle est de degré un et n’est pas pendante (c’est une arête isolée). Dans ces deux cas, la suppression de l’arête entraînerait la suppression d’une face (et même de deux faces dans le premier cas) et donc la perte d’une relation d’adjacence entre les deux régions incidentes à la face.
[a][b]
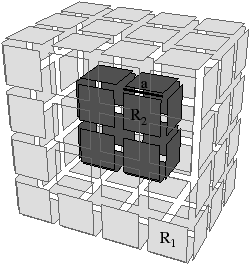
Figure 4.19: Cas pour lesquels les deux conditions de la Def. 69 sont nécessaires. (a) Le cas d’une arête a de degré deux qui ne doit pas être supprimée car elle n’est pas supprimable (cette configuration est obtenue en supprimant toutes les autres arêtes incidente à R2 et R3 qui étaient toutes supprimables et de degré deux ou pendantes). (b) Le cas d’une arête a supprimable mais qui ne doit pas être supprimée car elle n’est pas de degré deux (configuration obtenue en supprimant toutes les autres arêtes incidentes à R2). L’arête restante est n’importe quelle arête de la subdivision initiale et dépend de l’ordre de traitement des arêtes.
Mais il est nécessaire d’ajouter une condition pour supprimer les arêtes pendantes. En effet, une arête de degré deux dans la carte de niveau 1 peut devenir pendante après certaines suppressions d’arêtes (cf. Fig. 4.20). Il faut noter que ce type de cas ne se posait pas en dimension 2 car un sommet ne peut pas être pendant.
[a][b]
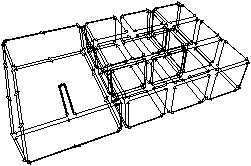
Figure 4.20: Le niveau 2 d’une image 3D en cours de construction. (a) La carte de niveau 1 de la Fig. 4.18. (b) La carte de niveau 2 en cours de construction. Certaines arêtes de degré deux ont été supprimées. L’arête en gras était de degré deux dans la carte de niveau 1 et est maintenant de degré un.
Ne pas supprimer les arêtes de degré un (à l’exception des arêtes pendantes) fait que nous n’allons pas supprimer une face composée d’une seule arête (cas de la représentation minimale de la sphère, comme pour la région R2 dans la Fig. 4.4.2), ni supprimer une arête interne à une face dont la suppression aurait pour conséquence que la face ne soit plus homéomorphe à un disque (cf exemple Fig. 4.21).
[a][b]
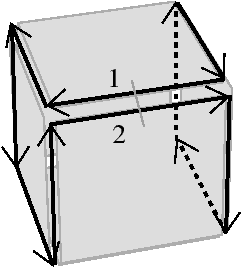
Figure 4.21: Cas d’une arête de degré un non pendante. (a) Une configuration composée de quatre régions, R0 étant la région infinie englobant les trois autres régions. (b) La face séparant R0 et R2 dans la carte de niveau 2 (en fait seule la demi-face est dessinée, il faudrait représenter la même demi-face du coté de R0). L’arête {1,2} est de degré un mais n’est pas pendante. Cette arête doit être conservée pour préserver la face homéomorphe à un disque, ou dit autrement afin de ne pas déconnecter l’orbite face en deux.
Les arêtes de degré un non pendantes sont appelées arêtes fictives car contrairement aux autres arêtes, elles ne représentent pas le bord d’une face frontière entre deux régions. Par opposition, les autres arêtes sont appelées arêtes réelles.
Pour supprimer toute les arêtes données par la Def. 69, nous devons être capables de tester si une arête est supprimable et de degré deux ou pendante.
Tester si une arête est supprimable se fait en testant pour un brin b de l’arête si β23(d)=β32(d) (cf. Def. 49). Si ce test est vrai pour un brin, alors il est vérifié pour chaque brin de l’arête5 et l’arête est supprimable par définition. Il faut alors tester si l’arête correspond à un des deux cas de la Def. 49 : une arête de degré deux, ou une arête pendante. L’arête est de degré un si les deux brins b et β2(d) appartiennent à la même face, c-à-d β2(d) ∈ ⟨β1⟩(d). Il est possible d’effectuer ce test en parcourant l’orbite ⟨β1⟩(d) et en vérifiant si le brin β2(d) est trouvé lors de ce parcours. Mais la complexité de cette opération est linéaire en nombre de brins de la face contenant l’arête. Comme ce test doit être fait pour chaque arête de la carte, cela nous donne une complexité quadratique pour la construction de la carte de niveau 2. Pour améliorer cette complexité, nous utilisons les arbres union-find [Tar75] qui permettent de manipuler efficacement des ensembles disjoints.
Cette structure de données est manipulée à l’aide de deux primitives : find qui retourne le représentant d’un élément donné, et union qui fusionne deux ensembles. L’intérêt de cette structure est que, en utilisant deux optimisations simples, la complexité amortie d’un ensemble de m opérations union-find sur un ensemble contenant n éléments est en O(n.α(m,n)) avec α(m,n) étant l’inverse de la fonction Ackermann qui est une fonction qui croit très lentement, et qui est inférieure à 5 dans les cas pratiques (cf. [Tar75] pour l’étude de complexité).
Lors de la création des volumes pour la construction du niveau 0, à chaque face est associé un arbre union-find étant le seul élément de son ensemble. Lors de la suppression d’une arête de degré deux, les deux arbres union-find des faces incidentes à l’arête (face(d) et face(β2(d))) sont fusionnées. Avec ce principe, tester si β2(d) ∈ ⟨β1⟩(d) se fait simplement en testant si find(d)=find(β2(d)). En utilisant les heuristiques sur les arbres union-find et l’étude de la complexité amortie des opérations, tester si une arête est de degré un s’effectue alors en temps constant, et la complexité de la construction de la carte de niveau 2 est linéaire en le nombre de brins de la carte.
Lorsque l’arête est de degré un, il reste à tester si elle est pendante ou non. La Fig. 4.22 montre les quatre configurations possibles d’une arête de degré un en fonction du degré des sommets de l’arête. Pour chaque sommet, nous distinguons le cas du sommet de degré un car le sommet est alors uniquement incident à l’arête supprimée, du cas du sommet de degré supérieur à un car le sommet est alors incident à au moins deux arêtes. Il y a deux cas distingués par sommet, et une arête est composée de deux sommets (car la carte de niveau 2 ne peut pas contenir de boucle), ce qui donne les quatre cas possibles de la Fig. 4.22. Pour chacun de ces cas, nous sommes capables de caractériser localement la configuration correspondante par un simple test sur le voisinage d’un brin de l’arête, les formules étant données dans la légende de la figure. De plus, chaque test est réalisé en temps constant. Les deux cas des Figs. 4.4.2 et 4.4.2 sont les cas des arêtes pendantes, les deux autres cas sont des arêtes fictives car l’arête considérée est de degré un mais non pendante.
[a] [b]
[c]
[d]
Figure 4.22: Les quatre configurations possibles de faces autour d’une arête de degré un en fonction du degré de ses sommets. (a) Les deux sommets sont de degré un : l’arête est isolée et donc fictive (de degré un et non pendante). β0(b)=β2(b) et β1(b)=β2(b). (b) Une arête pendante : un sommet est de degré un, l’autre de degré supérieur à un. β0(b)=β2(b) et β1(b) ≠ β2(b). (c) Une arête pendante : cas symétrique avec β1(b)=β2(b) et β0(b) ≠ β2(b). (d) Les deux sommets sont de degré supérieur à un, l’arête est fictive (de degré un et non pendante). β0(b)≠ β2(b) et β1(b)≠ β2(b).
Nous avons prouvé que les simplifications effectuées pour calculer le niveau 2 à partir du niveau 1 préservent la topologie de la partition en montrant que les propriétés suivantes sont vérifiées :
Le premier point garantit que les surfaces présentes dans la carte de niveau 1 sont préservées dans la carte de niveau 2 ; le second point garantit que chaque face est représentée par une seule orbite ⟨β1⟩ et donc que les surfaces sont représentées par des complexes cellulaires 2D, et le dernier point garantit que la topologie des surfaces est préservée (cf. [Dam08] pour plus de détails sur les propriétés des niveaux et les preuves).
Ces trois propriétés permettent de prouver que les nombres de Betti restent inchangés entre le niveau 1 et le niveau 2. En effet, le nombre de composantes connexes et le nombre de cavités sont donnés par le nombre de surfaces frontières : chaque région est représentée par une surface frontière pour son bord externe, et une surface frontière par cavité. Le nombre de tunnels est quant à lui lié au nombre de surfaces frontières, et à la caractéristique d’Euler de chaque surface (cf. Section 2.1.4 page ??).
Nous pouvons voir Fig. 4.23 la carte de niveau 2 de l’exemple utilisé Fig. 4.18. Cette carte est désormais composée de 16 sommets, 18 arêtes, 6 faces, et 4 volumes.
[a][b]
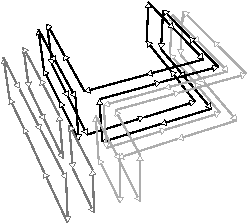
Figure 4.23: Le niveau 2 d’une image 3D. (a) La carte de niveau 1 de la Fig. 4.18. (b) La carte de niveau 2 dans laquelle toutes les arêtes de degré deux et les arêtes pendantes ont été supprimées.
La dernière passe de simplification concerne la suppression de sommets. Comme en dimension 2, nous devons supprimer les sommets supprimables et de degré deux afin de ne pas supprimer un sommet incident à une seule arête (cas du sommet supprimable mais de degré un), et pour ne pas supprimer un sommet incident à deux boucles (cas du sommet de degré deux mais non supprimable). En effet, dans les deux cas, la suppression du sommet entraînerait la disparition des arêtes et des faces incidentes, et donc la disparition d’une relation d’adjacence entre les volumes incidents. Mais un traitement spécifique est nécessaire pour obtenir une carte ne dépendant pas de la position des arêtes fictives. Ce traitement est basé sur le décalage des arêtes fictives.
Nous appelons sommet fictif un sommet incident uniquement à des arêtes fictives, et par opposition sommet réel un sommet incident à au moins une arête réelle.
La Def. 70 donne la définition de la carte de niveau 3 intégrant la suppression des sommets supprimables et de degré deux et le décalage des arêtes fictives.
Cette définition distingue deux cas pour les sommets réels et les sommets fictifs (cf. exemples Fig. 4.24). Tout d’abord pour les sommets réels, il existe au moins une arête réelle incidente. Le sommet doit être supprimé s’il est supprimable et de degré deux après avoir décalé toutes les arêtes fictives lui étant incidentes. Les deux conditions (supprimable et de degré deux) sont identiques au cas 2D et proviennent des mêmes considérations : chercher à supprimer les sommets entre deux arêtes distinctes en préservant les boucles qui sont les bords de faces frontières. Mais avant de tester ces conditions, nous commençons par décaler toutes les arêtes fictives incidentes au sommet. En effet, ces arêtes sont nécessaires pour préserver la topologie de la partition en conservant chaque face homéomorphe à un disque topologique, mais la position de ces arêtes n’est pas importante. Afin de garantir l’obtention de la carte minimale en nombre de cellules, nous devons garantir qu’un sommet n’est pas non supprimable à cause de la présence d’une arête fictive. En effet, nous obtiendrions alors une carte non minimale puisqu’il existe une autre carte avec moins de cellules, obtenue en changeant la position de l’arête fictive. L’étape de décalage des arêtes fictives résout ce problème en garantissant qu’un sommet réel est supprimé indépendamment de la position des arêtes fictives.
[a][b]
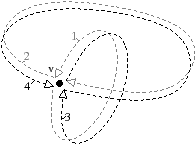
Figure 4.24: Les différents cas possibles de sommets : fictifs ou non, supprimables et de degré deux ou non. (a) Deux sommets satisfont les conditions de la Def. 70 et seront supprimés : v2 est non fictif, supprimable et de degré deux après avoir décalé les arêtes fictives incidentes ; v4 est fictif, supprimable et de degré deux après avoir décalé les arêtes fictives incidentes sauf une arête non boucle. Deux sommets ne satisfont pas les conditions et seront conservés : v1 est de degré trois après avoir décalé les arêtes fictives ; v3 est de degré un après avoir décalé les arêtes fictives. (b) Cas d’une représentation minimale d’un tore : le seul sommet v n’est pas supprimé car il est fictif et il n’existe pas d’arête non boucle incidente à v.
L’opération de décalage d’arête présentée au chapitre 3 (page ??) préserve la topologie de la partition car chaque arête décalée est ici de degré un. De ce fait, la modification est locale à la face et la seule modification topologique qui pourrait se produire est la déconnexion de la face en deux, ce qui n’est pas possible. De plus, il est facile de vérifier que le nombre de cellules de la partition reste constant avant et après le décalage d’arête. Dans la définition du niveau 3, après avoir décalé toutes les arêtes fictives incidentes au sommet réel, ce sommet n’est plus incident à une arête fictive et nous pouvons donc tester simplement s’il est supprimable et de degré deux. Si une arête réelle incidente au sommet considéré est une boucle, le sommet ne sera soit pas supprimable, soit pas de degré deux, ce qui garantit qu’aucune face ne disparaisse de par la suppression du sommet.
Pour les sommets fictifs, le principe est un peu différent : en effet, le décalage ne peut pas concerner toutes les arêtes fictives incidentes au sommet (car ce serait alors toutes les arêtes), mais il concerne toutes les arêtes fictives sauf une arête non boucle. Il y a donc deux sous cas selon qu’il existe une arête non boucle incidente au sommet ou non. Dans le premier cas (par exemple le sommet v4 dans la Fig. 4.4.3), plusieurs arêtes fictives dont au moins une non boucle se rejoignent «au milieu» d’une face. Cette configuration n’est pas minimale car les arêtes fictives servent uniquement à préserver la face homéomorphe à un disque. Il est possible dans ce cas de décaler toutes les arêtes sauf une non boucle, puis de supprimer cette arête qui est devenue pendante. Nous obtenons alors une carte avec moins de cellules et représentant les mêmes informations topologiques. Il faut noter que s’il existe plusieurs arêtes fictives non boucle incidentes au sommet, les configurations obtenues sont isomorphes quel que soit le choix de l’arête a utilisée pour le décalage des autres arêtes.
Le deuxième cas est celui d’un sommet fictif pour lequel il n’existe pas d’arête non boucle incidente. Ce cas correspond à la configuration minimale d’un tore à k tunnels, comme le sommet v de l’exemple de la Fig. 4.4.3. Dans cette configuration, le sommet ne peut alors pas être supprimé sans entraîner la suppression de la face entière incidente au sommet et donc la perte de l’information topologique représentée par cette face frontière. Pour cette raison ce type de sommet est conservé dans la Def. 70.
En pratique, nous testons les propriétés des sommets avant d’effectuer le décalagage des arêtes fictives pour des raisons d’efficacité. Pour cela, nous parcourons chaque arête incidente au sommet courant, en comptant le nombre d’arêtes non fictives #anf, ainsi que le nombre d’arêtes réelles et arêtes fictives non boucles #arnb et #afnb (ces nombres peuvent être calculés par un algorithme linéaire en nombre de brins incidents au sommet, en marquant les arêtes rencontrées). Si #anf>0, le sommet est réel, sinon il est fictif. Dans les deux cas, nous pouvons facilement caractériser les deux conditions de la Def. 70 :
[a][b]

Figure 4.25: Le niveau 3 d’une image 3D. (a) La carte de niveau 2 de la Fig. 4.23. (b) La carte de niveau 3 dans laquelle tous les sommets de degré deux ont été supprimés.
Nous pouvons voir Fig. 4.25 la carte de niveau 3 de l’exemple utilisée Fig. 4.23. Cette carte est désormais composée de 2 sommets, 4 arêtes, 6 faces, et 4 volumes. Elle est minimale : il n’est pas possible de supprimer une cellule en conservant toutes les faces frontières de l’image, et chaque face homéomorphe à un disque. Nous pouvons prouver que le processus de décalage d’arête couplé à la suppression de sommet permet bien d’obtenir un minimum global quel que soit la position initiale des arêtes fictives. En effet, les sommets sont considérés sans tenir compte de la position des arêtes fictives. De ce fait, au moment de traiter un sommet s, soit il satisfait les conditions de la Def. 70 et il est supprimé, soit il ne pourra jamais les satisfaire, quel que soient les autres suppressions et décalages effectués ultérieurement.
La carte de niveau 3 est, de manière similaire à la carte de niveau 2 en 2D, la carte combinatoire minimale représentant la partition de l’image en régions. Mais comme en 2D, nous devons ajouter un arbre d’imbrication des régions pour positionner entre elles les éventuelles composantes connexes de la carte. Cet arbre repose sur le même principe qu’en dimension 2 : les régions appartenant à la même composante 18-connexe sont regroupées au sein d’un même ensemble, ce qui permet de retrouver directement un brin par surface bordant les cavités d’une région donnée (cf. les explications données en Section 4.3.3, les seules différences étant le remplacement de la 4-connexité 2D en 6-connexité 3D, et de la 8-connexité 2D en 18-connexité 3D).
[a][b]
[c]
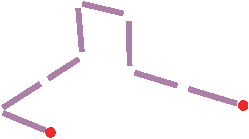
Figure 4.26: Exemples de plongements géométriques associés à différentes cellules de la carte. (a) Une face sphérique représentée par un ensemble de surfels. Cette face n’a pas de bord, donc aucun lignel n’est allumé. (b) Une face représentée par un ensemble de surfels, et bordée par une arête (une boucle) représentée par un ensemble de lignels. L’arête n’a pas de bord, il n’y a pas de pointel allumé. (c) Une arête représentée par un ensemble de lignels, ayant ses deux sommets extrémités allumés.
Pour décrire la géométrie, nous utilisons la même solution qu’en 2D : une matrice d’éléments intervoxels dans laquelle sont allumés les éléments appartenant aux frontières des régions (cf. les exemples de la Fig. 4.26) :
Chaque brin de la carte est associé avec un triplet (pointel, lignel, surfel) qui permet de retrouver la géométrie de n’importe quelle cellule non fictive. Les cellules fictives (sommets et arêtes) n’ont pas de géométrie car leur rôle est purement topologique. De plus, il n’est pas toujours possible d’associer à une arête fictive une courbe simple de lignels (par exemple dans le cas d’un tore à quatre trous, la carte correspondante est composée de huit arêtes fictives. Il n’est alors pas possible d’associer une géométrie à ces huit arêtes qui se rejoignent uniquement à leur extrémités en un même pointel, étant donné qu’un pointel peut être au maximum incident à six lignels).
La géométrie d’un sommet est directement obtenue par le pointel. La géométrie d’une arête est l’ensemble des lignels obtenus par un parcours dans la matrice à partir du lignel orienté du triplet (l’orientation du lignel est donnée par le couple (pointel,lignel)), en avançant de lignel en lignel jusqu’à tomber sur un pointel allumé ou à revenir sur le lignel initial. La géométrie d’une face est l’ensemble des surfels obtenus par un parcours dans la matrice à partir du surfel orienté (l’orientation étant donnée par le triplet), en parcourant tous les surfels voisins du surfel courant, non séparés par un lignel (cf. exemple Fig. 4.26 et l’article [Dam08] pour plus de détails).
Il existe un cas particulier pour les pointels incidents à un seul lignel. Ce cas se produit lorsqu’un lignel est incident à quatre surfels mais incident uniquement à deux régions (cf. exemple Fig. 4.27). Dans ce cas, le lignel est allumé car il est incident à plus de deux surfels, et les pointels extrémités du lignel sont incidents uniquement à ce pointel. Ces pointels doivent être allumés dans la matrice, afin que les extrémités de chaque arête non boucle soient bien composées de deux pointels allumés. Ce cas n’est pas possible pour les lignels, car un lignel ne peut pas être incident à un seul surfel par définition des régions et des frontières.
Comme en 2D, nous appelons carte topologique le modèle composé de la carte combinatoire de niveau 3, de l’arbre d’imbrication des régions, et d’une représentation de la géométrie (cf. exemple Fig. 4.28). Comme en 2D, le choix du modèle utilisé pour représenter la géométrie dépendra des besoins des applications, et n’est pas crucial pour nous, les principales difficultés portent en effet sur la définition du modèle minimal préservant les informations topologiques.
Nous pouvons voir Fig. 4.29 les différents cas résolus par la conservation des arêtes fictives. En effet, contrairement à la déconnexion de volume qui se produit uniquement en présence d’imbrication, le problème de déconnexion de face se pose lorsqu’une surface possède plusieurs bords. De plus, un problème se pose également pour les surfaces sans bord. Dans ces cas, la solution à base d’arbre d’imbrication n’est pas adaptée pour trois raisons :
Figure 4.29: Le problème de représentation de faces selon leur nombre de bords (en noir et épais sur les figures). (a) Une face comportant 3 bords, sans relation d’imbrication entre eux. (b) Une face sans bord. (c) et (d) Deux surfaces avec les mêmes bords mais pas la même topologie.
La préservation des arêtes fictives résout tous ces problèmes. En effet, avec ce type d’arête, chaque face de la carte est homéomorphe à un disque et le genre de chaque surface peut toujours être calculé en comptant le nombre de cellules la composant et en utilisant la formule d’Euler-Poincaré. En effet, ce type d’arête permet :
[a][b]
[c]
[d]
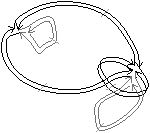
Figure 4.30: Représentation avec des arêtes fictives des exemples de la Fig. 4.29. Les arêtes fictives sont dessinées en noir. La suppression de ces arêtes entraîne la disparition de l’objet ou une déconnexion de face.
Après avoir défini le modèle des cartes topologiques, nous nous sommes intéressés à la définition d’opérations sur ces modèles. La première opération que nous avons étudiée est l’opération d’extraction qui permet de construire une carte topologique à partir d’une image étiquetée. Cette phase est en effet l’étape préalable à toutes les autres opérations. Nous avons ensuite étudié les opérations de fusion et de division de régions, qui sont les opérations de base permettant de modifier la subdivision de l’image en régions. De plus, ces opérations nous permettent par la suite de définir des algorithmes de segmentation utilisant la carte topologique. Nous donnons ici simplement les principes généraux de ces opérations sans rentrer dans le détail. Le lecteur intéressé pourra trouver plus d’informations dans les différentes références indiquées lors de la présentation des opérations.
Nous avons proposé trois algorithmes permettant de construire la carte topologique, en 2D et 3D, à partir d’une image étiquetée. Un premier algorithme, dit naïf, consiste à construire la carte de niveau 0 puis à la simplifier progressivement selon les définitions des différents niveaux (cf. Fig. 4.31 pour une illustration en 2D). Cet algorithme a l’avantage d’être simple. Son inconvénient principal est de devoir créer la carte de niveau 0 qui peut contenir énormément de brins. De ce fait, cette carte peut ne pas tenir en mémoire et donc empêcher le calcul de la carte minimale, malgré le fait qu’elle contienne beaucoup moins de brins.
Figure 4.31: Le principe de construction naïf d’une carte topologique 2D. (a) Une image 2D étiquetée. (b) La carte de niveau 0 initiale. (c) La carte de niveau 1 obtenue après suppression de chaque arête séparant deux pixels de même étiquette. (d) La carte de niveau 2 obtenue après la suppression de chaque sommet supprimable et de degré deux.
Pour résoudre ce problème, nous avons proposé un second algorithme d’extraction, dit par balayage. Son principe consiste à balayer l’image (cf. la Fig. 4.32 pour une illustration en 2D). Pour chaque pixel/voxel, un carré/cube est créé, et ajouté à la carte en cours de construction. Pour cela, nous conservons un brin correspondant à l’élément précédent du parcours, qui permet de raccrocher le nouvel élément. Ensuite, la carte est localement simplifiée autour du nouvel élément, en supprimant les cellules caractérisées dans les définitions des niveaux de simplification. L’avantage de cet algorithme est de ne pas représenter toute la carte de niveau 0 en mémoire puisque les simplifications sont effectuées de manière progressive. De plus, afin de traiter simplement les éléments situés au bord de l’image, nous avons créé un bord initial qui est replié sur lui-même (cf. exemple Fig. 4.5.1). Ce bord revient à replier l’image 2D sur un cylindre, en identifiant les pixels à droite de l’image avec les pixels à gauche de l’image et sur la ligne suivante, ce qui ramène le parcours de l’image à toujours avancer le pixel courant.
Figure 4.32: Déroulement de quelques étapes de la construction par balayage de la carte topologique représentant une image 2D étiquetée. Les pixels hachurés appartiennent à la région infinie. Le trait pointillé représente la relation β1 permettant de «fermer» le bord. (a) La carte initiale représentant le bord supérieur et gauche (correspondante à l’image de la Fig. 4.5.1). (b) Création et couture du carré représentant le pixel (1,1). (c) Les cellules sont localement simplifiées autour du pixel (1,1) lorsqu’elles vérifient les conditions. (d) Création et couture du carré représentant le pixel (2,1). (e) Carte obtenue après le traitement du pixel (2,1). (f) Création du carré associé à un pixel (4,1) appartenant à la dernière colonne. (g) Carte obtenue après le traitement du pixel (4,1). Comme l’image est plaquée sur un cylindre, cette configuration est équivalente à la carte présentée en (h).
En 3D, nous effectuons deux repliements afin de replier l’image sur un tore volumique. De ce fait, le balayage de l’image se ramène également à uniquement faire avancer le voxel courant (cf. [Dam01] pour plus de détails. La version 2D est également décrite précisément dans [DBF04] et celle 3D dans [Dam08]). Cet algorithme a une complexité linéaire en nombre d’éléments de l’image. De plus, il nécessite un seul balayage, le calcul de l’arbre d’imbrication des régions étant réalisé dans une seconde étape, après l’extraction de la carte, avec un algorithme linéaire en le nombre de brins de la carte.
Enfin, nous avons défini un troisième algorithme d’extraction, dit optimal, utilisant la notion de précode. Un précode est une configuration locale de pixels/voxels dans une fenêtre de taille 2n (n étant la dimension de l’espace, donc 2 ou 3). Le principe de cet algorithme est d’associer à chaque précode possible un traitement modifiant localement la carte (cf. les deux exemples de la Fig. 4.33). L’algorithme d’extraction se ramène alors à balayer l’image (de manière similaire à l’algorithme par balayage) et à appliquer la modification associée au précode courant. Cet algorithme est alors optimal car pour chaque configuration, il effectue un nombre minimal d’opérations de mise à jour de la carte. En 2D, il existe 15 précodes différents. En découpant l’étude de ces précodes en fonction des niveaux de simplification, nous avons montré que des configurations pouvaient être factorisées en introduisant la notion de précode partiel, un précode dans lequel certain pixels/voxels peuvent avoir n’importe quelle valeur. Cette factorisation nous a amené à réduire le nombre de cas à 10, sans aucun surcoût de traitement. Le gain n’est pas très important en 2D mais il devient beaucoup plus intéressant en dimension 3 où le nombre total de précodes existant est de 4140, ce qui rend difficile le développement de toutes les fonctions associées. En factorisant ces précodes à l’aide de la notion de précode partiel, nous avons réduit le nombre de cas à 379, et l’avons encore diminué à 129 en regroupant les configurations symétriques. Ce nombre de cas reste important, mais le développement des différentes fonctions redevient envisageable, ce qui n’était pas le cas avec le nombre initial de cas. Une première version de cet algorithme à base de précodes a été présentée dans [BDF00]. La version 2D est décrite dans [DBF04], et la version 3D est décrite en détail dans [Dam01].
Précode Carte initiale Carte finale
Figure 4.33: Deux exemples de précodes, le premier étant un précode partiel. Pour chaque précode, il faut transformer la carte initiale en la carte finale. Cette transformation est équivalente à la création d’un carré représentant le pixel, puis à la suppression locale des cellules autour de ce pixel. Mais l’opération est ici optimale car nous évitons la création inutile de brins, et nous réutilisons lorsque c’est possible les brins existants.
Les premières opérations de modification que nous avons définies sont la fusion et la découpe de régions. Ce travail a été initié durant le stage de master recherche de Patrick Resch [DR02, DR03] avant d’être poursuivi et généralisé durant la thèse d’Alexandre Dupas [DD08a, DD09, Dup09]. Les opérations présentées ici le sont pour les cartes topologiques 3D, mais sont bien entendu définies pour les cartes topologiques 2D de manière équivalente.
De manière générale, l’opération de fusion va s’appuyer sur les opérations de suppression, et l’opération de découpe va s’appuyer sur les opérations d’insertion. La principale difficulté des opérations de modification dans le cadre des cartes topologiques est de garantir la préservation des propriétés de ce modèle, c’est-à-dire principalement la minimalité de la carte combinatoire, et conserver chaque face homéomorphe à un disque. Il faut également garantir le lien cohérent entre la carte combinatoire et l’arbre d’imbrication des régions, la propriété sur le brin représentant, et le lien entre la carte et le plongement géométrique. Pour simplifier les modifications, nous découpons souvent l’opération en deux étapes : la première étape effectue les modifications sans se préoccuper des contraintes, et la deuxième étape s’occupe uniquement des mises à jour liées à ces contraintes.
La première opération définie est la fusion de régions. Nous avons proposé deux approches pour cette opération (détaillées dans les Algorithmes 4.34 et 4.5.2) : la première, dite fusion locale, qui va fusionner un ensemble connexe de régions dans une seule région ; la seconde approche, dite fusion globale, qui va effectuer la fusion simultanée de plusieurs ensembles de régions connexes, chaque ensemble étant fusionné dans une région. Nous avons comparé ces approches et montré que la première est plus intéressante dans le cadre d’un faible nombre de régions à fusionner, comme par exemple dans une utilisation interactive où les régions sont sélectionnées par un utilisateur, et que la seconde est plus intéressante dans le cadre de la fusion d’un grand nombre de régions, comme par exemple dans le cas d’une segmentation d’images par agrégation de régions.
Figure 4.34: Algorithme : Approche locale de la fusion de régions
- Entrées : Une carte topologique C;
Un ensemble 6-connexe de régions E.- Résultat : Fusionne les régions de E dans C.
choisir la plus petite région de E comme région résultante;
Pour chaque brin b appartenant aux régions de E faire
Si region(β3(b)) ∈ E alors
marquer b et β3(b);mettre à jour l’arbre d’imbrication des régions;
supprimer toutes les faces intérieures (préalablement marquées);
simplifier les cellules incidentes aux faces supprimées;
L’Algorithme 4.34 donne le principe général de l’approche locale de la fusion. Il comporte trois étapes principales :
La première étape garantit que le brin représentant b de la région résultante de l’union vérifiera bien la contrainte des brins représentants (c-à-d par β3, nous obtenons un brin d’une région plus petite que la région de b). Ensuite, le marquage des faces intérieures se fait simplement en testant pour chaque brin b des régions de S si β3(b) est un brin d’une région de E. Si oui la face est intérieure aux régions de l’ensemble et elle devra être supprimée. La mise à jour de l’arbre d’imbrication va consister à supprimer les régions de E et à les remplacer par une seule région, mais également à détecter des éventuelles nouvelles imbrications créées par la fusion. Cette étape est réalisée avant la suppression des faces intérieures afin de pouvoir utiliser ces faces pour retrouver les futures relations d’imbrication. Ensuite, il reste à mettre à jour la carte combinatoire, tout d’abord en supprimant les faces intérieures (en utilisant les opérations de 2-suppression, tout en mettant également à jour la géométrie dans la matrice d’inter-éléments), puis en simplifiant la carte pour la rendre minimale (en utilisant les définitions des différents niveaux, et les opérations de 1- et 0-suppression).
L’approche globale de la fusion de régions consiste à fusionner simultanément plusieurs ensembles 6-connexes de régions. Son principe est de séparer les modifications de la carte topologique du processus de fusion de régions proprement dit. Dans un premier temps, les régions sont manipulées avec un haut niveau d’abstraction, à l’aide d’arbres union-find. Puis, dans un second temps, les fusions de haut niveau sont retranscrites dans la partition représentée par une carte topologique en supprimant les cellules inutiles et en construisant le nouvel arbre d’imbrication des régions.
L’Algorithme 4.5.2 présente le principe de la fusion de régions par approche globale. Il prend en paramètres une carte topologique C et une fonction Oracle qui indique si deux régions doivent être fusionnées. L’algorithme modifie la carte topologique de sorte que tous les ensembles 6-connexes de régions désignés par l’oracle soient effectivement fusionnés dans la partition finale. Il comporte trois étapes principales :
Figure 4.35: Algorithme : Approche globale de la fusion de régions
- Entrées : Une carte topologique C ;
Une fonction Oracle.- Résultat : Fusionne toutes les régions par composante 6-connexe en fonction de l’oracle.
Pour chaque brin b ∈ C faire
Si Oracle(region(b),region(β3(b))) alors
fusionner symboliquement region(b) et region(β3(b));
supprimer toutes les faces intérieures;
simplifier la carte topologique;
construire le nouvel arbre d’imbrication des régions;
Lors de la première étape de l’algorithme, chaque région est initialisée comme racine de son propre arbre union-find. La fusion symbolique de deux régions consiste alors simplement à faire l’union des deux arbres union-find correspondants. À la fin de cette étape, chaque arbre union-find est un ensemble 6-connexe de régions à fusionner. Un brin b appartient à une face intérieure si region(b)=region(β3(b)). Les étapes suivantes de l’algorithme sont identiques à celles de la fusion locale : supprimer les faces intérieures, simplifier la carte et mettre à jour l’arbre d’imbrication. La différence avec la fusion locale est que ces modifications sont faites sur toute la carte, et non plus de manière locale. De ce fait, nous préférons reconstruire totalement l’arbre d’imbrication plutôt que de le mettre à jour : en effet, comme le nombre de modifications dans cet arbre peut être important, il est moins coûteux de le recalculer entièrement.
L’opération inverse de la fusion de régions est la division d’une région. L’objectif est d’obtenir plusieurs régions en découpant une région initiale. De manière générale, la division de région utilise un guide, par exemple une surface, pour découper la région initiale. Le nombre de régions résultantes dépend alors de la géométrie de la région initiale et de la géométrie du guide utilisé pour la découpe. Une division particulière est l’éclatement d’une région. Il s’agit de la division d’une région de manière à ce que chaque région résultante ne contienne qu’un seul voxel.
L’Algorithme 4.5.2 présente les différentes opérations réalisées pour éclater une région en régions élémentaires. Il prend comme paramètres une carte topologique et une région à éclater.
Figure 4.36: Algorithme : Éclatement d’une région en régions élémentaires
- Entrées : Une carte topologique C;
Une région R.- Résultat : Éclatement dans C de la région R en régions élémentaires.
D ← ensemble de brins vide;
Pour chaque surface S du bord de R faire
ajouter l’un des brins de S à D;
éclater le volume incident aux brins de D en volumes élémentaires;
construire une nouvelle région par volume;
mettre à jour l’arbre d’imbrication;
simplifier les bords des régions éclatées;
Son principe consiste à éclater chaque surface bordant la région R en ce que nous appelons des volumes élémentaires. Un volume élémentaire est un volume qui correspond à un voxel de l’image (de même pour une face/arête élémentaire pour les surfels/lignels). Cette étape se réalise en insérant des sommets sur les bords des faces jusqu’à avoir des arêtes élémentaires. Puis nous saturons chaque face en insérant toutes les arêtes possibles jusqu’à obtenir uniquement des faces élémentaires, et enfin nous saturons le volume en insérant toutes les faces possibles jusqu’à obtenir uniquement des volumes élémentaires (cf. exemple Fig. 4.37). Nous associons ensuite une nouvelle région à chaque volume élémentaire et mettons à jour l’arbre d’imbrication des régions en remplaçant la région éclatée par ces nouvelles régions, et en modifiant éventuellement les relations d’imbrication qui existaient avec R. Enfin, nous devons simplifier le bord des nouvelles régions car il se peut que celles touchant le bord de R aient des cellules non minimales.
[a][b]
[c]
[d]
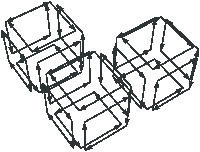
Figure 4.37: Exemple d’éclatement d’une région en volumes élémentaires. (a) La région initiale composée de trois faces : deux représentées par une seule arête qui est une boucle, et une troisième qui est composée de trois arêtes, dont une fictive. (b) Résultat après l’éclatement des arêtes non fictives en arêtes élémentaires. (c) Résultat après la saturation des faces : chaque face de la région est maintenant élémentaire. (d) Carte finale obtenue après la saturation de la région en volumes élémentaires.
L’éclatement d’une région construit une partition généralement sursegmentée de la région initiale. Une partition aussi détaillée n’est pas souhaitable dans la plupart des applications. D’une part le temps de calcul de cette opération est long, et d’autre part l’espace mémoire nécessaire pour représenter la partition éclatée est très important, surtout lorsque la région éclatée est grande. Nous avons donc défini une opération de division d’une région qui est plus adaptée aux besoins pratiques : la division de régions par un guide. Le guide est donné par un ensemble de surfels qui doit être séparant, c’est-à-dire couper la région R en au moins deux régions.
L’Algorithme 4.5.2 présente l’opération de division d’une région par un guide. Il prend en paramètres une carte topologique, une région et un ensemble de surfels qui est un guide de division pour la région sélectionnée.
Figure 4.38: Algorithme : Division d’une région par un guide
- Entrées : Une carte topologique C ;
Une région R ;
Un guide G.- Résultat : Division dans C de la région R par le guide G.
éclater les arêtes et les faces du bord de la région R;
construire le guide de division défini par G;
coudre le guide aux bords de la région R;
construire l’arbre d’imbrication des nouvelles régions;
simplifier la carte topologique;
La première étape de l’algorithme consiste à éclater le bord de la région à diviser en faces élémentaires, de manière similaire à l’étape d’éclatement d’une région, mais sans effectuer la dernière étape qui éclate les volumes. L’étape suivante construit le guide de division dans la carte topologique, en construisant une face carrée par surfel du guide, et en cousant correctement ces faces entre elles selon les configurations des surfels dans G. Ce guide est ensuite fusionné dans la carte topologique. Comme nous avons éclaté le bord de la région R, et par construction du guide, nous n’avons que des arêtes élémentaires. La fusion consiste alors simplement à interclasser les faces autour des arêtes du bord du guide. Le résultat de cette opération est le remplacement du volume associé à la région R par l’ensemble des volumes décrits par le guide et les bords de la région (cf. exemple Fig. 4.39). Il faut alors effectuer la mise à jour de l’arbre d’imbrication, puis simplifier la carte pour la rendre minimale.
[a][b]
[c]
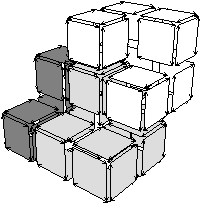
Figure 4.39: Exemple de découpe d’une région par un guide. (a) La région initiale après que son bord ait été éclaté en faces élémentaires. (b) Le guide utilisé pour découper cette région. (c) Résultat obtenu après l’insertion du guide dans la région qui est découpée en trois volumes. Il reste à simplifier les bords de ces volumes et à mettre à jour l’arbre d’imbrication.
Dans ce chapitre, nous avons défini la carte topologique 2D et 3D, un modèle de représentation d’une image étiquetée. Ce modèle utilise une carte combinatoire minimale afin de représenter la partition de l’image en cellules ainsi que les relations d’incidence et d’adjacence entre ces cellules. Cette carte est liée à un modèle décrivant la géométrie de ses cellules, qui peut être une matrice d’inter-éléments, mais qui peut aisément être changé selon les besoins des applications. Enfin, un arbre d’imbrication des régions permet de compléter la représentation du modèle en décrivant les relations entre les différentes composantes connexes de la carte.
La carte topologique est définie de manière progressive, en utilisant les opérations de base définies au chapitre 3. Cette définition progressive simplifie les définitions ainsi que l’étude des problèmes de déconnexion, car chaque niveau est défini par l’application d’un seul type d’opération. C’est ce type de définition qui nous a permis d’étendre de manière assez directe la carte topologique 2D en dimension supérieure, chose qui semblait beaucoup plus délicate avec les modèles proposés précédemment dans la littérature, soit de par leur définition directe, soit à cause de leur algorithme de construction. Cette définition progressive a également simplifié la définition d’algorithmes d’extraction à partir d’une image, en facilitant l’intégration progressive des opérations de simplification, et en proposant un moyen direct de regrouper les cas à traiter.
Nous avons également présenté brièvement quelques opérations définies dans le cadre des cartes topologiques : tout d’abord l’extraction d’une carte topologique à partir d’une image étiquetée, puis les opérations de fusion et de découpe qui sont les opérations de modification de base d’une carte topologique.
Nous avons dans ce chapitre utilisé les cartes combinatoires, mais comme l’ensemble des définitions utilisent les opérations de base, ces définitions sont également valides sans aucune modification pour les cartes généralisées. Le choix des cartes combinatoires a été ici guidé par le développement d’un logiciel (présenté chapitre 7) qui demande deux fois moins d’espace mémoire pour les cartes combinatoires que pour les cartes généralisées.
Nous souhaitons poursuivre ces travaux afin d’étendre la carte topologique en dimension quelconque. Les niveaux de simplification s’étendent de manière directe : en dimension n, une carte topologique serait définie par n niveaux de simplification, chaque niveau i, 1≤ i ≤ n étant la simplification du niveau i−1 en utilisant la (n−i)-suppression. Un arbre d’imbrication serait utilisé pour conserver les relations entre les différentes composantes connexes de la carte. Le seul problème qui reste partiellement ouvert est celui des éléments fictifs. Pour tout i, 1≤ i < n−1, nous aurions des i-cellules fictives pour conserver chaque (i+1)-cellule homéomorphe à une boule. La conservation de ces cellules doit pouvoir se faire en détectant les cellules de degré un, mais cela doit être étudié plus précisément. Par contre, pour obtenir la carte minimale, nous devons décaler ces cellules afin qu’elles n’empêchent pas d’autres suppressions. C’est ce point qui reste à étudier plus précisément : le décalage de i-cellule, et son utilisation pour garantir la préservation de la topologie des objets, tout en garantissant également l’obtention de la carte minimale. Nous allons également poursuivre le développement d’autres opérations, pour proposer un ensemble d’outils permettant de réaliser la plupart des opérations possibles de traitement d’images.
Nous allons maintenant présenter une extension hiérarchique des cartes que sont les pyramides généralisées. L’objectif de ce modèle est de manipuler différentes représentations d’un même objet, par exemple afin de conserver plusieurs niveaux de détails, ou pour décrire différentes subdivisions d’un même objet, chacune pouvant correspondre à une sémantique particulière. Ces pyramides sont à nouveau définies à partir des opérations de base présentées au chapitre précédent.
Dans ce chapitre, nous étudions une extension des cartes afin de décrire une hiérarchie de partitions, ainsi que les liens entre ces partitions : les pyramides de cartes. Ce type de représentation permet par exemple de décrire un objet à différentes résolutions, ou de manipuler différentes subdivisions d’un même objet, chaque subdivision pouvant correspondre à une certaine description sémantique.
Il existe de nombreux travaux ayant étudié des représentations hiérarchiques. Comme pour les modèles de représentation d’images présentés au chapitre précédent, de nombreuses recherches ont tout d’abord porté sur l’utilisation de graphes pour définir des pyramides de graphes d’adjacence [Mee89, MMR91, JM92, Jol03], avant d’être étendus aux pyramides de graphes duaux [WK94, KM95, Kro95]. Par la suite, compte-tenu des avantages des cartes combinatoires par rapport aux graphes, des recherches ont porté sur la définition des pyramides de cartes combinatoires [BK01, BK02, BK03a] mais uniquement en 2D. Il faut également citer d’autres travaux en modélisation géométrique, où différentes structures ont été proposées, et notamment le modèle simplicial multi-résolution [dFPM97], ou des modèles ad hoc basés sur les cartes généralisées [Lev99, Gui00, Fra04]. Ces différentes structures hiérarchiques ont soit l’inconvénient de ne pas représenter toutes les informations topologiques (cellules, incidences et adjacences), soit d’être définies uniquement en 2D, soit d’être définies spécifiquement pour un domaine précis.
Pour ces raisons, nous avons étudié la définition d’une structure de données qui soit à la fois générique, c’est-à-dire pouvant s’adapter à différents domaines d’utilisation et en dimension quelconque, et complète, c’est-à-dire qu’elle représente toutes les cellules et relations d’incidence et d’adjacence : c’est ce que nous avons appelé les pyramides généralisées. Nous avons ensuite étudié les propriétés de cette structure de données, le lien entre ses différents niveaux, et différentes représentations possibles. Ce travail est le résultat de la thèse de Carine Grasset-Simon [Sim06] et a été présenté dans [SDL05a, SDL05b, SDL06].
L’organisation de ce chapitre est la suivante. Nous commençons Section 5.1 par introduire et définir les pyramides généralisées. Puis Section 5.2 nous présentons les orbites généralisées, une extension des orbites entre deux niveaux non nécessairement consécutifs d’une pyramide. Enfin, Section 5.3, nous définissons trois représentations différentes de ces pyramides. Ces trois représentations sont équivalentes, mais sont plus ou moins compactes en mémoire, au détriment bien entendu d’une représentation plus ou moins explicite des différentes informations. Enfin nous concluons cette partie et donnons des perspectives Section 5.4.
Une pyramide de cartes généralisées, appelée pyramide généralisée, est une structure hiérarchique composée d’une séquence de nG-cartes, où chaque niveau est une réduction du niveau précédent obtenue par l’application des opérations de suppression et contraction de cellules.
Nous présentons Def. 71 la définition des pyramides généralisées basée sur les opérations de contraction et suppression.
Chaque nouveau niveau de la pyramide est obtenu par simplification du niveau précédent en supprimant et contractant certaines cellules. Nous conservons ici les notations introduites à la Section 3.2 lors de la définition de l’opération de suppression et contraction simultanées, en ajoutant un exposant pour indiquer le niveau concerné dans la pyramide. De ce fait, ∀ l: 0 ≤ l <m et ∀ i: 0 ≤ i ≤ n, nous notons Sil et Cil les ensembles de i-cellules du niveau l qui sont respectivement supprimées et contractées, et BVil l’ensemble des brins survivants du niveau l, i-voisins de i-cellules supprimées ou contractées.
Par définition de l’opération de suppression et contraction simultanées (cf. Def. 53 page ??), ces cellules doivent vérifier les conditions suivantes :
Un exemple de pyramide de 2G-cartes est donnée Fig. 5.1.1.
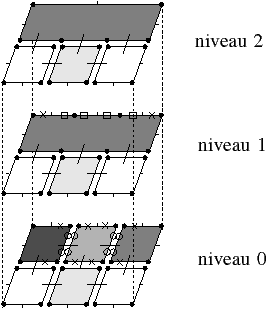
Figure 5.1: Exemple de pyramide de 2G-cartes composée de trois niveaux. Les brins 0-supprimés (resp. 1-supprimés) sont marqués par □ (resp. ∘); les brins voisins d’une cellule supprimée sont marqués par ×.
Suite à cette définition des pyramides généralisées, il est facile de prouver qu’un brin ne peut disparaître qu’une seule fois au cours de la construction de la pyramide, c’est-à-dire à un seul niveau de la pyramide et suite à une seule opération : par la suppression ou la contraction d’une cellule. Nous parlons de brin survivant au niveau l pour un brin qui n’appartient pas à une cellule contractée ou supprimée de ce niveau, et notons BSl pour l’ensemble des brins survivants du niveau l. Ces brins sont reliés par ϕl aux brins de BSl+1. Plus formellement, ϕl est la bijection ϕl:BSl → Bl+1 induite par l’opération de suppression et contraction simultanées utilisée lors de la définition du niveau l+1 à partir du niveau l. Cette bijection est la relation successeur existant entre les brins survivants du niveau l de la pyramide et les brins du niveau l+1. De plus, la bijection inverse (ϕl)−1 est la relation prédécesseur existant entre les brins du niveau l+1 et les brins survivants du niveau l. Nous notons nivb le dernier niveau dans lequel le brin b existe. Si b appartient à une cellule supprimée ou contractée à un niveau l<m, alors nivb=l, sinon (b est survivant à chaque niveau), nivb=m.
Après avoir défini la notion de pyramide, il est nécessaire d’étudier le moyen de retrouver les informations d’un niveau en propageant les informations des niveaux précédents. Ces notions sont liées aux chemins de connexions («connecting walks» en anglais) initialement définis par Brun et Kropatsch dans le cadre des pyramides combinatoires (cf. [BK01]) en 2D. Intuitivement, un chemin de connexion entre deux brins reliés par αi au niveau j permet de retrouver les brins du niveau j−1 parcourus lors de la redéfinition de αi par l’opération de suppression et contraction simultanées. La définition de ces chemins peut ensuite être étendue entre deux niveaux non consécutifs. Mais cette notion n’est pas suffisante pour manipuler les informations au sein d’une pyramide. En effet, une information est souvent associée à une orbite d’un certain niveau (par exemple les coordonnées d’un point associées à une orbite sommet). De ce fait, nous nous sommes intéressés à l’extension de la notion d’orbite permettant de retrouver tout les brins d’un niveau inférieur qui composent une orbite d’un niveau donné : c’est la notion d’orbite généralisée. Cette notion permet de propager les informations associées aux orbites d’un niveau inférieur à n’importe quel niveau de la pyramide.
Un chemin de connexion, défini entre deux niveaux consécutifs de la pyramide, est une séquence de brins du niveau inférieur séparant deux brins liés par un αi au niveau supérieur (cf. exemple Fig. 5.1.2). La liaison entre deux brins d’un même niveau est, par définition de l’opération de suppression/contraction simultanée, déduite d’une succession de liaisons du niveau précédent, effectuées en tenant compte de l’état des brins parcourus, à savoir supprimé, contracté ou survivant. Ainsi, la définition du chemin de connexion entre deux niveaux consécutifs a et a+1, pour un brin b donné et pour une involution αi donnée, reprend les termes de la définition de l’involution αia+1. Nous notons Ch(i,a,d)(b) le chemin de connexion défini entre les niveaux a et d (a ≤ d), pour l’involution αi et pour le brin b ∈ Bd.
Les chemins de connexion peuvent être définis de manière récursive (cf. Def. 72) ou itérative (cf. Def. 73). Dans les deux cas, le principe de base est similaire : il consiste à regarder l’état du brin courant, et selon les cas (supprimé, contracté, survivant) à utiliser la liaison en relation avec l’opération correspondante, ou à changer de niveau pour récupérer les informations du niveau précédent.
L’idée principale de la définition récursive repose sur le fait qu’un chemin de connexion entre les niveaux a et d est une concaténation de sous-chemins entre les niveaux a et d−1 séparant les brins du niveau d−1 qui relient b et b′ et qui appartiennent à des cellules supprimées ou contractées au niveau d−1 (étant donné deux chemins C1 et C2, nous notons (C1,C2) le chemin obtenu par concaténation de C1 et C2).
| i si u est impair, |
| i+1 si u est pair et bu ∈ Sid−1, |
| i−1 si u est pair et bu ∈ Cid−1. |
Comme nous pouvons le voir sur la Fig. 5.2, le chemin de connexion Ch(0,0,2)(1), défini entre les niveaux 0 et 2 et reliant les brins 1 et 10 correspond à la concaténation des sous-chemins Ch(0,0,1)(1)=(2), Ch(1,0,1)(2)=(3,4,5), Ch(0,0,1)(5)=(6), Ch(1,0,1)(6)=(7,8,9) et Ch(0,0,1)(9)=(10) composant respectivement les liaisons existant entre les brins séparant les brins 1 et 10 au niveau 1.
[a][b]
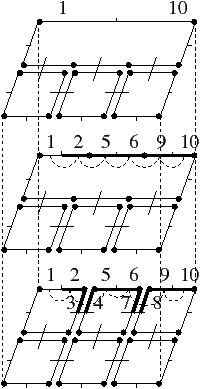
Figure 5.2: Chemins de connexion. La pyramide considérée est celle de la Fig. 5.1.1. (a) Exemples de chemin entre deux niveaux consécutifs : les brins des chemins de connexion Ch(1,0,1)(2) et Ch(1,0,1)(6) sont dessinés en gras au niveau 0 de la pyramide. Ces brins se situent respectivement entre les brins 2 et 5, et entre les brins 6 et 9 où 5 = 2 α11 et 9 = 6 α11 : Ch(1,0,1)(2) = (3,4,5) et Ch(1,0,1)(6) = (7,8,9). (b) Exemple de chemin entre deux niveaux non consécutifs : les brins du chemin de connexion Ch(0,1,2)(1) sont dessinés en gras au niveau 1 de la pyramide. Ces brins se situent entre les brins 1 et 10 où 10 = 1 α02 : Ch(0,1,2)(1) = (2,5,6,9,10). Les brins du chemin de connexion Ch(0,0,2)(1) sont dessinés en gras au niveau 0 de la pyramide : Ch(0,0,2)(1)=(2,3,4,5,6,7,8,9,10).
Une autre manière de définir la notion de chemin de connexion est de le faire itérativement et non récursivement. L’idée repose sur le fait que connaissant l’état du brin courant (supprimé ou contracté) et l’involution ayant permis d’arriver sur ce brin, il est possible de déduire la prochaine involution du chemin.
En se plaçant entre deux niveaux consécutifs a et a+1, nous utilisons les propriétés suivantes sur le chemin issu de b par αi :
Nous pouvons remarquer que par définition des i-cellules, le chemin peut parcourir différentes i-cellules, supprimées ou contractées au niveau a :
Soient bu le dernier brin du chemin qui a été découvert, et αku−1a l’involution qui a permis de le découvrir. Nous pouvons alors remarquer que :
Afin d’exprimer la prochaine involution (αku) en fonction de la dernière involution (αku−1), les quatre points précédents peuvent être reformulés de la manière suivante :
Ces quatre formules, étant donné un brin et la dernière involution, nous donnent la prochaine involution, et donc le prochain brin du chemin. Les constatations précédentes, réalisées dans le cas d’un chemin de connexion défini entre deux niveaux consécutifs, peuvent être généralisées dans le cas où nous considérons un chemin entre deux niveaux quelconques, ce qui nous permet ainsi de déduire la définition itérative suivante :
| ||||||
| ||||||
Les chemins de connexion vérifient différentes propriétés prouvées dans [Sim06] :
D’autre part, de la même manière qu’une involution liant deux brins est symétrique, le chemin de connexion liant deux brins est «réversible». En effet, soit C un chemin de connexion liant les brins b et b αid auquel est ajouté b en premier élément. La séquence de brins inverse de C correspond au chemin de connexion liant b αid à b auquel est ajouté b αid en premier élément. D’autre part, si deux ensembles connectants ouverts ne sont pas égaux alors ils n’ont aucun brin en commun. De plus, les deux définitions des chemins de connexion donnent directement deux algorithmes permettant de parcourir ces chemins, le premier récursif basé sur la Def. 72, et le second itératif basé sur la Def. 73.
Nous notons DBC(i,a,d)(b) le dernier brin du chemin de connexion Ch(i,a,d)(b).
Étant donné un chemin de connexion Ch(i,a,d)(b), nous pouvons déduire deux ensembles de brins : l’ensemble connectant ouvert Ech(i,a,d)∘(b), et l’ensemble connectant fermé Ech(i,a,d)(b). Intuitivement, le premier ensemble correspond à l’ensemble des brins à l’intérieur du chemin de connexion et le second correspond à l’ensemble des brins du chemin, extrémités incluses.
| ∅ si Ch(i,a,d)(b)=() |
| Ech(i,a,d)∘(b)⋃{b,b′} sinon, où b′ =DBC(i,a,d)(b) |
Tout niveau d’une pyramide généralisée est construit à partir du niveau précédent en effectuant des suppressions ou contractions de cellules. Ainsi, toute cellule supprimée ou contractée à un niveau a une incidence directe sur la construction des cellules et plus généralement des orbites composant le niveau suivant. Si un chemin de connexion Ch(i,d−1,d) permet de tenir compte des modifications occasionnées par la disparition de i-cellules situées entre deux i-cellules survivantes en les parcourant partiellement, il ne permet pas de tenir compte des i-cellules disparues non situées entre deux i-cellules survivantes.
Nous pouvons voir Fig. 5.3 le problème que cela occasionne lorsque les chemins de connexion sont utilisés pour retrouver par exemple les faces d’un niveau d−1 qui ont fusionnées en une seule face F au niveau d. Nous retrouvons seulement les faces qui sont incidentes au «bord» de la face F.
[a][b]
[c]
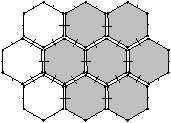
Figure 5.3: (a) Les niveaux d−1 et d d’une pyramide de 2G-cartes. Le niveau d est obtenu à partir du niveau d−1 par suppression des quatorze arêtes marquées par ∘. En grisé la face F pour laquelle nous cherchons l’ensemble des faces du niveau d−1 qui ont fusionné pour former F. (b) En grisé, les six faces obtenues en utilisant les chemins de connexion à partir des brins survivants. (c) En grisé, l’ensemble des sept faces que nous souhaiterions retrouver et qui correspond à l’ensemble des faces qui ont été fusionnées pour former F.
En effet, comme nous pouvons le voir dans la Fig. 5.4 qui détaille les différents chemins de connexion utilisés, les chemins de connexion Ch(1,d−1,d) permettent de découvrir les arêtes a à h situées entre deux arêtes survivantes, mais pas les arêtes i à n non situées entre deux arêtes survivantes.
[a][b]
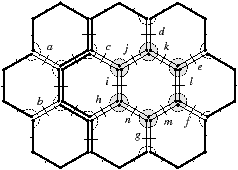
Figure 5.4: Niveau d−1 de la pyramide de la Fig. 5.1.3 où le niveau d est obtenu par suppression des arêtes a à n. Le parcours de chaque chemin de connexion Ch(1,d−1,d) est symbolisé en pointillé, et les arêtes survivantes au niveau d sont dessinées en gras. (a) Les chemins de connexion Ch(1,d−1,d) permettent de découvrir partiellement les arêtes a à h situées entre deux arêtes survivantes. Mais ces chemins ne permettent pas de découvrir les arêtes i à n non comprises entre deux arêtes survivantes. (b) En grisé, des chemins appliquant les mêmes règles de parcours que les chemins de connexion Ch(1,d−1,d) mais partant d’un brin supprimé n’appartenant pas à une arête découverte partiellement par un chemin de connexion Ch(1,d−1,d).
L’idée des chemins de connexion étendus est de permettre de parcourir toutes les cellules disparues entre deux niveaux consécutifs pour ainsi tenir compte de toutes les cellules étant intervenues dans la construction d’une cellule donnée. Pour cela, la notion de chemin de connexion est étendue à tout brin b de la pyramide de la manière suivante :
Les chemins de connexion étendus sont donc l’extension des chemins de connexion définis pour tout brin et non plus seulement les brins survivants. Comme les chemins non-étendus, ces chemins étendus peuvent être définis de manière récursive et de manière itérative.
| i si u est impair, |
| i+1 si u est pair et bu ∈ Sid−1, |
| i−1 si u est pair et bu ∈ Cid−1. |
| si b ∈ (Sid−1 ⋃ Cid−1) : br appartient à Bd, |
| si b ∈ (Sjd−1 ⋃ Cjd−1) avec j ≠ i : br appartient à Bd−1. |
| ||||||
| ||||||
Les chemins de connexion étendus vérifient des propriétés similaires à celles des chemins de connexion. Tout d’abord, les deux définitions, itérative et récursive, proposées pour ces chemins sont équivalentes et définissent un unique chemin à partir d’un brin. De plus, deux chemins de connexion étendus, observés entre deux mêmes niveaux sont soit disjoints soit ils ont un ou plusieurs sous-chemins consécutifs en commun.
De manière similaire aux chemins de connexion, nous notons DBCE(i,a,d)(b) le dernier brin d’un chemin de connexion étendu, et nous définissons l’ensemble connectant étendu ouvert EchE(i,a,d)∘(b), et l’ensemble connectant étendu fermé EchE(i,a,d)(b). Ces ensembles connectants étendus sont à la base de la définition des orbites généralisées.
| ∅ si ChE(i,a,d)(b)=() |
| EchE(i,a,d)∘(b)⋃{b,b′} sinon, où b′ =DBCE(i,a,d)(b) |
Dans le cadre des pyramides de graphes [MMR91] ou des pyramides combinatoires [BK03b], souvent utilisées pour stocker différentes partitions d’une même image 2D, la notion de champ récepteur («receptive field» en anglais) permet de retrouver l’ensemble des pixels qui ont été fusionnés pour former une région de l’image dans une certaine partition. De façon plus générale, un champ récepteur représente en 2D l’ensemble connexe des cellules de dimension deux (représentées par les sommets du graphe) du niveau initial qui ont été fusionnées pour former une cellule de dimension deux observée à un niveau donné de la pyramide.
Dans la pyramide de graphes de la Fig. 5.5, le champ récepteur associé au sommet s situé au troisième niveau de la pyramide est l’ensemble des sommets dessinés en noir au niveau initial. Dans le cas où cette pyramide représente une pyramide d’images, le champ récepteur correspond à l’ensemble des pixels de l’image initiale (sommets du niveau initial de la pyramide) qui composent la région observée (sommet d’un niveau supérieur de la pyramide).
[a][b]
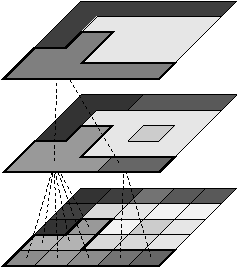
Figure 5.5: Champ récepteur dans une pyramide de graphes. (a) Pyramide de graphes avec en noir les nœuds des deux premiers niveaux qui correspondent au nœud s du troisième niveau. (b) Pyramide d’images correspondante.
Puisque les cartes généralisées ne représentent pas uniquement les cellules de plus grande dimension, mais toutes les cellules et même plus généralement toutes les orbites composant l’objet observé, il est nécessaire de pouvoir retrouver des informations quel que soit le type de cellule ou d’orbite observée. D’autre part, l’information utile n’étant pas nécessairement située au niveau initial de la pyramide, il est nécessaire de pouvoir retrouver l’information désirée dans n’importe quel niveau de la pyramide. Pour répondre à ces besoins, nous avons défini la notion d’orbite généralisée comme une extension des champs récepteurs en toute dimension, pour toute orbite, et entre deux niveaux quelconques.
Nous allons tout d’abord introduire la notion d’orbite généralisée de manière intuitive, en étudiant pour cela l’exemple de la Fig. 5.6, où l’orbite observée est l’arête l (nous parlons de cellule généralisée pour désigner l’orbite généralisée associée à une orbite correspondant à une cellule, et de sommet généralisé, arête généralisée …pour une orbite généralisée correspondant à un sommet, une arête …) :
La formation de l’arête l est alors due à :
Puisque ces arêtes sont intervenues lors de la formation de l’arête l, elles doivent toutes faire partie de l’arête généralisée associée à l’arête l. Ainsi, suivant le niveau considéré, nous obtenons les arêtes généralisées suivantes :
Plus généralement, la i-cellule généralisée associée à une i-cellule c est l’ensemble des i-cellules :
[a][b]
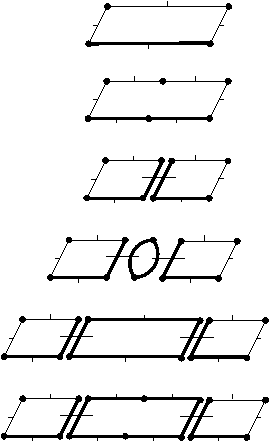
Figure 5.6: Présentation intuitive d’une orbite généralisée. (a) Pyramide de 2G-cartes comptant six niveaux obtenus par suppressions d’arêtes (∘), contractions d’arêtes (•), suppression de sommets (□) et contraction de faces (filled square). (b) À chaque niveau de la pyramide, les arêtes composant l’arête généralisée associée à l’arête l sont dessinées en gras.
L’idée principale du parcours des brins composant une orbite généralisée est d’utiliser une méthode similaire à celle mise en pratique pour parcourir les brins d’une orbite, en remplaçant l’utilisation des αi par l’utilisation des Ch(i,a,d). Par définition, une orbite est l’ensemble des brins pouvant être atteints à partir d’un brin donné en utilisant les involutions définissant l’orbite. Par exemple, l’orbite ⟨α0,α1⟩(b) qui, en 3D, correspond à l’ensemble des brins appartenant à une même face d’un même volume, est obtenue à partir du brin b en effectuant un parcours utilisant les involutions α0 et α1.
Par analogie, nous introduisons la suite ( OGi(K,a,d)(b) ) qui définit le parcours de l’orbite généralisée OG(K,a,d)(b) associée à l’orbite <>(K)d(b) du niveau d, et observée au niveau a.
| et | ∀ i: i > 0, |
| OGi(K,a,d)(b) = ∪j ∈ K ∪b′ ∈ OGi−1(K,a,d)(b) EchE(j,a,min{d, nivb′+1})(b′). |
Cette suite est croissante, bornée, et stationnaire car il existe p, 0 ≤ p ≤ |Ba|, tel que ∀ i: i ≥ p: OGi(K,a,d)(b) = OGp(K,a,d)(b). La suite ( OGi(K,a,d)(b) ) converge donc en un nombre fini d’itérations, et sa limite peut donc être considérée.
Dire que b′ est un brin de OG(K,a,d)(b) est équivalent à dire qu’il existe une suite de brins {b1, …, bq+1}, qui lie les brins b et b′ au moyen d’une succession de chemins de connexion étendus (ou d’une partie d’un chemin de connexion étendus).
Les orbites généralisées vérifient les propriétés suivantes, prouvées dans [Sim06] :
De manière générale, les orbites les plus utilisées sont les cellules. Il en est de même pour les orbites généralisées, et nous avons donc étudié plus particulièrement les propriétés des orbites généralisées associées à des cellules, que nous appelons cellules généralisées et nous notons CG(i,a,d)(b) pour la i-cellule généralisée calculée au niveau a et associée à la i-cellule du niveau d contenant le brin b.
Dans le cas où la pyramide considérée ne contient aucune suppression ni contraction de i-cellule, les i-cellules généralisées respectent une propriété particulièrement intéressante : deux i-cellules généralisées sont nécessairement disjointes ou confondues. Il faut noter que cette propriété n’est pas vérifiée dans le cas général.
Cette propriété est illustrée dans l’exemple de la Fig. 5.7. Dans cette pyramide de 2G-cartes, il n’y a pas eu de contraction ni suppression de face. De ce fait, les faces généralisées observées dans cette pyramide sont soit distinctes, soit confondues. Les niveaux 0 et 1 sont tous les deux composés de quatre faces généralisées distinctes associées chacune à une face du niveau 2. Trois d’entre elles sont respectivement associées aux faces du niveau 2 contenant les brins 14, 15 et 16, et la quatrième correspond à deux faces généralisées confondues et respectivement associées aux faces du niveau 2 contenant les brins 1 et 13. Nous pouvons remarquer au niveau 2, que si la face grise en tant que cellule d’une subdivision est représentée dans la G-carte par deux orbites faces du fait que la G-carte ne soit plus connexe, les faces généralisées calculées à partir de ses bords sont confondues car elles utilisent les informations des niveaux précédents dans lesquels la carte était connexe.
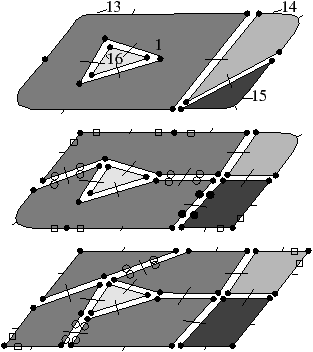
Figure 5.7: Pyramide de 2G-cartes comportant trois niveaux. Les niveaux 1 et 2 sont respectivement obtenus à partir des niveaux 0 et 1 par suppression des sommets marqués par □, suppression des arêtes marquées par ∘ et par contraction des arêtes marquées par •. Les faces généralisées associées aux orbites faces contenant les brins 1, 13, 14, 15 et 16 sont représentées à chaque niveau par différents niveaux de gris. Remarquons que les deux orbites faces contenant respectivement les brins 1 et 13 et représentant les deux bords déconnectés d’une même face sont associées à la même face généralisée. Dans cette pyramide ne comportant ni suppression ni contraction de face, les faces généralisées sont soit disjointes, soit confondues.
Une pyramide de cartes généralisées peut être représentée de façon plus ou moins explicite selon les besoins des applications. Il s’agit ici d’un problème classique de définition d’une structure de données concrète : il est nécessaire d’une part de compléter la structure en fonction des informations nécessaires pour l’application, et d’autre part de choisir en fonction des informations manipulées et des opérations utilisées, l’équilibre optimal entre information explicitement et implicitement représentées (compromis d’efficacité espace mémoire / temps de calcul).
De multiples représentations des pyramides de cartes généralisées sont possibles : nous décrivons ici trois représentations «caractéristiques» : explicite, hiérarchique et implicite. La représentation explicite correspond exactement à la définition des pyramides généralisées, chaque niveau de la pyramide est explicitement représenté ainsi que les liens entre les niveaux. La représentation hiérarchique définit les différents niveaux par un même ensemble de brins évitant ainsi une certaine redondance de l’information. Enfin, la représentation implicite est particulièrement intéressante pour le stockage sur disque puisque seul le niveau de base est explicitement représenté, les autres niveaux pouvant être déduits en conservant les opérations effectuées pour les réaliser.
La Fig. 5.8 illustre chacune de ces trois représentations dans le cas d’une pyramide de 2G-cartes. Cette pyramide est composée de trois niveaux, les deuxième et troisième niveaux étant respectivement obtenus par suppression de deux arêtes et de deux sommets.
[a][b]
[c]
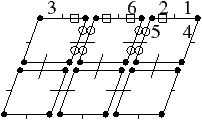
Figure 5.8: Trois représentations d’une même pyramide de 2G-cartes. (a) Représentation explicite : chaque niveau de la pyramide est explicitement représenté. Un □ (resp. ∘) marque un brin d’une 0-cellule (resp. une 1-cellule) à supprimer. (b) Représentation hiérarchique : les brins composant les différents niveaux ne sont pas dupliqués, mais toutes les involutions des différents niveaux sont représentées. Les cellules supprimées sont marquées de la même manière que dans la représentation explicite. Chaque brin est ici dessiné dans le dernier niveau de la pyramide où il existe. Quand deux brins liés par αi sont dessinés dans le même niveau, leur liaison αi est dessinée de manière usuelle. Sinon, les liaisons α01 et α00 entre deux brins de deux niveaux différents sont représentées par des lignes marquées par ◇, et les liaisons α10 par des lignes marquées par filled diamond. (c) Représentation implicite : elle est composée d’une unique G-carte correspondant au niveau initial de la pyramide. Un ∘ (resp. un □) marque un brin d’une 1-cellule du niveau 0 (resp. une 0-cellule du niveau 1) à supprimer.
La représentation explicite d’une pyramide généralisée est très proche de la définition de celle-ci. Chaque niveau de la pyramide est explicitement représenté ainsi que chaque bijection existant entre ces niveaux. Comme l’illustre la Fig. 5.9, cette représentation contient autant de cartes généralisées que la pyramide compte de niveaux, et les liaisons bijectives successeur-prédécesseur existant entre les brins de deux niveaux consécutifs sont également présentes. Ainsi, tout brin à tout niveau est lié à son prédécesseur et à son successeur, mis à part les brins du niveau initial de la pyramide qui n’ont pas de prédécesseur, et les brins disparus ou du dernier niveau de la pyramide qui n’ont pas de successeur.
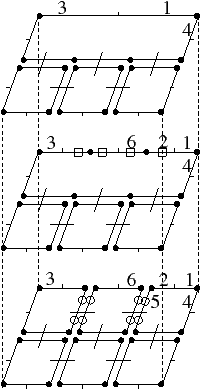
niveau 0 α00 α10 α20 marque 1 2 4 1 2 1 5 2 niveau 1 α01 α11 α21 marque 1 2 4 1 2 1 6 2 S0 niveau 2 α02 α12 α22 marque 1 3 4 1
Figure 5.9: Représentation explicite de la pyramide de la Fig. 5.8. Le tableau associé précise les images des brins 1 et 2 pour chaque niveau et chaque involution.
Afin de différencier, à chaque niveau de la pyramide, les brins appartenant à une cellule supprimée ou contractée des brins survivants, deux marques sont associées à chaque brin éliminé, indiquant d’une part l’opération concernée (contraction ou suppression), et d’autre part la dimension de la cellule concernée dans l’élimination. Bien sûr, ces marques respectent les contraintes de cohérence des pyramides de G-cartes (par exemple si un brin est marqué par une marque d’opération et une marque de dimension, tous les brins de la cellule concernée possèdent les mêmes marques).
Ce type de représentation est intéressant du point de vue théorique car les différents niveaux et les relations sont plus simples à manipuler lorsqu’ils sont explicites. Il est également intéressant pour manipuler les niveaux de manière indépendante : chaque niveau étant une G-carte, il est simple de conserver un niveau en mémoire et de laisser les autres niveaux sur disque.
La représentation hiérarchique d’une pyramide généralisée est plus compacte que la représentation explicite. En effet, tenant compte de la bijection existant entre les brins survivants d’un niveau et les brins du niveau suivant, elle limite la redondance en identifiant ces deux ensembles de brins (Ba+1 = Ba − (Sa ∪ Ca), ∀ a: 0≤ a < m).
Cette représentation est composée d’un unique ensemble de brins, celui du niveau initial de la pyramide, sur lequel sont définies (éventuellement de façon partielle) les différentes involutions des différents niveaux de la pyramide. Un exemple illustrant la représentation hiérarchique d’une pyramide de 2G-cartes est donné Fig. 5.10. Dans cette représentation nous associons au brin 1 (resp. au brin 2) trois suites, une pour chaque involution α0, α1, et α2. Ainsi, la première suite indique que le brin 1 (resp. 2) est lié par α0 au brin 2 aux niveaux 0 et 1, puis au brin 3 au niveau 2 (resp. au brin 1 aux niveaux 0 et 1). Une deuxième suite indique qu’il est lié par α1 au brin 4 aux trois niveaux (resp. au brin 5 au niveau 0, et au brin 6 au niveau 1). Enfin une troisième suite indique qu’il est lié à lui-même par α2 aux trois niveaux également (resp. à lui-même aux niveaux 0 et 1). Une optimisation possible pour compacter ces informations consiste à associer à chaque brin une suite ne comportant (pour chaque involution) que les brins différents ainsi que le niveau auquel l’involution d’un brin est modifiée. Pour l’exemple de la Fig. 5.10, trois suites seront associées au brin 1. La première, correspondant à α0, ne comportera que deux éléments (0,2) et (2,3), indiquant que le brin 1 est lié par α0 au brin 2 du niveau 0 au niveau 1 inclus, puis au brin 3 à partir du niveau 2. Les deuxième et troisième suites ne comporteront chacune qu’un seul élément, respectivement (0,4) et (0,1), indiquant que le brin 1 est respectivement lié par α1 et α2 aux brins 4 et 1 à partir du niveau 0.
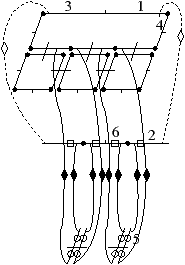
brin 1 marque -1.5exliaisons niveaux 0 1 2 α0 2 2 3 α1 4 4 4 α2 1 1 1
brin 2 marque S0 -1.5exliaisons niveaux 0 1 2 α0 1 1 α1 5 6 α2 2 2
Figure 5.10: Représentation hiérarchique de la pyramide de la Fig. 5.8. Les tableaux associés précisent les images par α0, α1 et α2 des brins 1 et 2 pour chaque niveau.
D’autre part, et de la même manière que pour la représentation explicite, deux marques sont associées à chaque brin éliminé : la première indique l’opération appliquée pour éliminer ce brin, la deuxième indique la dimension de la cellule concernée par l’opération.
Ce type de représentation est intéressant dans les traitements top-down où l’on commence à traiter un objet à un faible niveau de résolution avant d’éventuellement aller étudier certaines parties de manière détaillée. Il est proche du modèle proposé dans [KCB09] pour représenter des surfaces de subdivision, et de celui proposé dans [Fra04] pour représenter des bâtiments sous forme hiérarchique.
La représentation implicite est la représentation compacte d’une pyramide généralisée. Cette représentation tient compte du fait que chaque niveau est déduit du niveau précédent, et peut donc être construit à partir du niveau initial si la séquence des différentes suppressions et contractions effectuées à chaque niveau est conservée en mémoire.
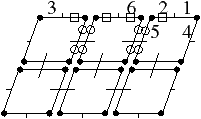
brins liaisons marque α0 α1 α2 1 2 4 1 2 1 5 2 S01
Figure 5.11: Représentation implicite de la pyramide de la Fig. 5.8. Le tableau associé présente les images par α0, α1 et α2 des brins 1 et 2 au niveau initial de la pyramide.
Ainsi, cette représentation se compose d’une unique G-carte correspondant au niveau initial de la pyramide (cf. exemple Fig. 5.11), et trois marques sont associées à chaque brin lorsque celui-ci disparaît à un niveau. De même que pour les deux premières représentations, une marque indique l’opération ayant entraîné la disparition de la cellule incidente à ce brin, et une deuxième indique la dimension de cette cellule. Une troisième marque indique le niveau auquel cette opération est appliquée. Nous pouvons remarquer que ce système de marquage ne laisse aucune ambiguïté, puisqu’une cellule ne peut disparaître qu’une seule fois, et n’est donc marquée qu’une fois au plus.
Ce type de représentation est intéressant pour stocker une pyramide de manière compacte. C’est une généralisation nD de la représentation proposée en 2D dans [BK03a, BK06].
Dans [Sim06], nous avons prouvé que ces trois représentations étaient équivalentes, et nous avons effectué une étude de complexité (mémoire et temporelle) comparative mettant en avant les avantages et inconvénients de chacune d’elle.
Dans ce chapitre nous avons présenté la définition des pyramides généralisées, en donnant leurs principales propriétés, et en définissant les notions importantes de chemin de connexion et d’orbite généralisée. Ces deux notions permettent en effet de faire le lien entre les différents niveaux de la pyramide. Nous avons également défini trois représentations possibles de ces pyramides qui sont plus ou moins compactes en mémoire. L’intérêt de ces pyramides est de représenter différentes subdivisions d’un même objet, et d’autoriser la navigation entre ces subdivisions au travers des cellules et de leurs raffinements. De plus, nous profitons des définitions formelles des cartes et des opérations de contraction et de suppression afin de garantir la validité de la structure.
Ces pyramides généralisées se définissent à nouveau à partir des opérations de base (contraction/suppression) définies au chapitre 3. De ce fait, il est possible de transposer les définitions de la carte topologique présentée au chapitre précédent pour que les différents niveaux de simplification soient conservés au sein d’une pyramide. Il suffit pour cela que chaque niveau de simplification devienne un nouveau niveau dans la pyramide et plus une modification «sur place» de la carte du niveau précédent. Enfin, nous avons utilisé ici des cartes généralisées pour profiter de leur définition homogène en toute dimension, mais ce travail peut être porté de manière directe aux cartes combinatoires en utilisant les algorithmes de conversion présentés au chapitre 2. Il faut noter que ce travail a débuté dans [FB09b, FB09a] où les auteurs définissent les opérations de contraction et de suppression, et la notion de chemin de connexion pour les cartes combinatoires.
Dans [Sim06], nous avons également étudié d’autres aspects autour des pyramides non présentés dans ce chapitre. Nous avons tout d’abord défini des opérations de modification locale d’une pyramide. Le principe de ces opérations est de fournir une opération autorisant la modification du marquage des cellules d’un niveau de la pyramide : des cellules qui étaient supprimées ou contractées ne le sont plus, et à l’inverse des cellules qui survivaient deviennent marquées à supprimer ou à contracter. Ce type d’opération est intéressant car il autorise une modification locale de la pyramide, par exemple pour remettre en question la fusion de deux faces dans un niveau précis, sans avoir à recalculer entièrement la pyramide. La problématique sous-jacente est appelée le «relinking». Il faut en effet étudier l’impact de la modification locale sur les niveaux suivants de la pyramide. En effet, par exemple le fait de ne plus supprimer une cellule dans un niveau peut entraîner qu’une cellule qui était supprimée dans le niveau suivant ne soit plus supprimable. Nous avons proposé deux définitions de mise à jour d’une pyramide, qui dépendent de la manière dont les propagations sont effectuées, et nous avons prouvé que les pyramides obtenues après modification sont identiques à celles que nous aurions obtenues par construction (cf. [Sim06] pour le détail de ces opérations).
Plus récemment, nous avons commencé l’étude des pyramides dites «top-down». Le principe de ces pyramides est d’être défini de manière inverse par rapport aux pyramides présentées dans ce chapitre (qui sont appelées «bottom-up» afin de les différencier). Une pyramide top-down est donc la donnée d’une séquence de cartes, où chaque niveau est un raffinement du niveau précédent obtenue par l’application des opérations d’insertion et d’éclatement de cellules. Ce type de pyramide à l’avantage de mieux correspondre à un processus de construction par raffinement, où une zone d’intérêt d’un niveau est raffinée au niveau suivant. Nous avons utilisé ce type de pyramide dans un projet de traitement de segmentation de grandes images histologiques (de taille jusqu’à 320002 pixels), où l’utilisation de méthode bottom-up n’est pas envisageable. De plus, nous avons défini une notion de pyramide tuilée permettant de s’affranchir du problème lié à la taille des images. Nous avons ainsi pu proposer un modèle qui peut être chargé tuile par tuile en mémoire, les autres parties étant basculées sur disque (cf. [GBD09, GDB09, GBD10, GDB10] pour plus de détails).
Les perspectives de ce chapitre concernent principalement l’utilisation des pyramides et la définition d’opérations, ces deux problématiques étant fortement liées car le besoin d’opérations spécifiques apparaît souvent en lien avec des utilisations pratiques. Nous avons commencé à étudier l’utilisation des pyramides de cartes 2D et 3D dans le but de proposer des méthodes de segmentation multi-échelle (qui seront évoquées au chapitre 7) mais ces travaux doivent être poursuivis afin de valider les apports de ces structures pour la résolution de problématiques précises. Nous souhaitons pour cela approfondir les travaux autour des problématiques liées à l’image, dans des méthodes de segmentation ou de reconnaissance. L’idée est d’utiliser une pyramide représentant un même objet à différentes échelles, puis de combiner les résultats des différentes échelles pour proposer des méthodes plus précises mais aussi plus rapides. En effet, en montant dans les niveaux supérieurs de la pyramide, le nombre d’éléments diminue et donc les temps de traitement également.
Nous souhaitons pour cela nous intéresser à la définition d’opérations spécifiques et à la manière dont elles utilisent les différents niveaux de la pyramide, afin d’être améliorées. Nous souhaitons également étudier l’utilisation des pyramides en modélisation géométrique, où nous envisageons de définir des opérations de modélisation multi-échelles, là encore en s’appuyant sur les liens entre les cellules des différents niveaux. Une nouvelle fois, nos définitions génériques nD montrent leur avantages en autorisant différentes applications en différentes dimensions. Une dernière perspective de recherche concerne la possibilité de compacter plusieurs niveaux d’une pyramide en un seul. L’objectif est ici de diminuer l’espace mémoire nécessaire à la représentation d’une pyramide, mais également les temps de parcours puisqu’il y aura moins de niveaux différents à traverser. Nous souhaitons pour cela étudier des méta-opérations regroupant différentes suppressions et contractions, en autorisant les cellules à ne plus être disjointes, tout en garantissant l’absence de perte d’information.
Nous allons maintenant présenter des opérations de calcul d’invariants topologiques sur les cartes. L’objectif de ce chapitre est de fournir ces opérations afin de pouvoir par la suite s’en servir pour caractériser les objets, ou encore pour guider ou contrôler des opérations.
Après avoir défini les modèles combinatoires de représentation de subdivisions dans les chapitres précédents, nous nous intéressons maintenant aux opérations de calcul d’invariants topologiques. En effet, un des intérêts des modèles présentés est qu’ils décrivent la topologie des objets manipulés. Il est donc important d’être capable d’utiliser ces informations au sein d’opérations, et pour cela il est nécessaire de pouvoir calculer des invariants topologiques.
Une spécificité de notre approche est l’utilisation des opérations de suppression et contraction pour simplifier un objet donné, ce qui permet soit de calculer plus simplement l’invariant topologique recherché, soit d’accélérer ce calcul car le nombre de cellules est beaucoup moins important. Pour cela, nous devons garantir que les opérations de simplification ne modifient pas la topologie de l’objet ce qui assure l’absence de perte d’information par rapport à l’objet initial. Nous faisons dans ce chapitre cette étude pour l’opération de suppression, le cas de la contraction pouvant se déduire directement par propriété de dualité. En dimension n, nous étudions seulement la caractéristique d’Euler-Poincaré. Nous avons également étudié trois autres invariants : les nombres de Betti, le schéma polygonal canonique, et les groupes d’homologie, mais pour le moment uniquement en 2D ou 3D.
Nous avons introduit Section 2.1.4 (page ??) la notion d’invariant topologique, et détaillé deux invariants numériques : la caractéristique d’Euler-Poincaré et les nombres de Betti. Nous allons montrer dans ce chapitre comment calculer ces invariants sur des objets décrits par des cartes. Mais avant, nous commençons par introduire Section 6.1 deux autres invariants topologiques qui sont le schéma polygonal canonique (un polygone canonique décrivant une surface) et les groupes d’homologie (des invariants classiques de la topologie algébrique).
Nous présentons simplement les notions de base des groupes d’homologie, et seulement de manière intuitive, le lecteur intéressé pourra consulter les références [Gib81, Hat02]. Ensuite, nous présentons Section 6.2 la mise à jour locale des nombres de cellules d’une subdivision lors des opérations de simplification, ce qui fournit directement un algorithme de calcul de la caractéristique d’Euler-Poincaré. Puis, Section 6.3, nous utilisons ce résultat pour proposer un algorithme de calcul des nombres de Betti d’une subdivision 3D orientable. Section 6.4 nous donnons une méthode de calcul du schéma polygonal canonique d’une surface 2D fermée, et Section 6.5 nous présentons deux algorithmes de calcul des groupes d’homologie 2D, et 3D dans le cas où l’objet est orientable. La Section 6.6 conclut et donne des perspectives à ce chapitre.
Toute surface S (2-variété) fermée peut être représentée par un polygone P, appelé schéma polygonal [Sti80, Gib81]. C’est un polygone dans lequel chaque arête est orientée et étiquetée avec une lettre de telle manière que chaque lettre soit l’étiquette de deux arêtes différentes du polygone. Ce polygone correspond à la surface obtenue en identifiant chaque couple d’arêtes ayant la même étiquette, en respectant l’orientation (cf. exemple Fig. 6.1).
Pour obtenir un schéma polygonal à partir d’une surface, il faut tout d’abord subdiviser la surface en sommets, arêtes et faces, orienter chaque arête de manière arbitraire, et étiqueter chaque arête avec une lettre distincte des lettres utilisées pour les autres arêtes. Il faut alors découper au maximum la surface le long des arêtes de la subdivision, jusqu’à ce que la surface soit homéomorphe à un disque. Il ne reste plus qu’à supprimer les arêtes se trouvant au milieu de la surface afin d’obtenir un seul polygone, qui lorsque les arêtes de même étiquette sont identifiées en respectant l’orientation, va donner une surface homéomorphe à la surface initiale.
Il existe plusieurs schémas polygonaux associés à la même surface, ce qui complexifie la comparaison des surfaces. L’exemple de la Fig. 6.1 montre deux schémas polygonaux qui sont tous deux associés à un tore. Il est possible d’associer un mot à chaque schéma polygonal en partant d’une arête du polygone et en lisant les lettres rencontrées en tournant dans un sens donné, sachant qu’une lettre est inversée lorsque l’arête est d’orientation opposée par rapport au sens de parcours. Pour l’exemple de la Fig. 6.1, en partant de l’arête a à gauche sur le dessin, et en tournant dans le sens trigonométrique, nous obtenons le mot abab, et pour l’exemple de la Fig. 6.1, le mot obtenu à partir de l’arête étiquetée a à gauche sur le dessin est le mot abcbac. Ce mot est cyclique car l’arête de départ du polygone est quelconque : par exemple les mots abcbac et acabcb sont identiques.
[a]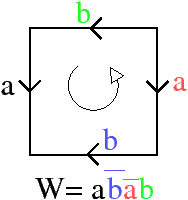
[b]
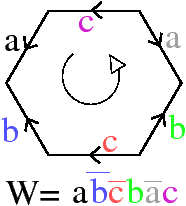
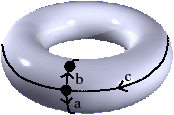
Figure 6.1: Exemple de schéma polygonal. (a) Un polygone composé de quatre arêtes, et la subdivision du tore correspondante. (b) Un polygone composé de six arêtes, et la subdivision du tore correspondante.
Pour résoudre ce problème de différents schémas polygonaux représentant la même surface, le schéma polygonal canonique a été défini [Bra22, VY90, FK97]. Ce schéma polygonal est unique et caractérise la topologie de la surface. Il est en lien direct avec le théorème de classification des surfaces (cf. Théorème 1 Section 2.1.4, page ??). Il existe trois formes différentes selon le type de surface considérée :
Tous les sommets du polygone associé au schéma polygonal canonique sont identifiés en un seul sommet, et toutes les arêtes sont donc des boucles (sauf dans le cas de la sphère).
Par exemple, le schéma polygonal canonique d’un tore est le mot abab (c’est l’exemple de la Fig. 6.1), le schéma polygonal canonique du plan projectif est le mot aa, et celui de la bouteille Klein (qui est la somme connexe de deux plans projectifs) est aabb.
Grâce au théorème de classification des surfaces, nous savons que le schéma polygonal canonique classifie totalement la topologie de la surface qu’il représente. Mais ce type de théorème n’existant pas en 3D, nous devons utiliser des invariants topologiques afin de décider si deux surfaces sont topologiquement différentes. Un invariant particulièrement intéressant pour cela est l’homologie. Le principe est d’associer à tout espace topologique X de dimension n une famille de n+1 groupes commutatifs, appelés groupes d’homologie. Ces groupes sont caractérisés par des générateurs qui sont en bijection avec des sous-ensembles de cellules de la subdivision, chaque générateur étant défini à homotopie près (les éléments de chaque classe pouvant s’obtenir par des déplacements continus). De ce fait, les groupes d’homologie peuvent être décrits de manière algébrique par ces ensembles de cellules.
Une i-chaîne (chaîne de dimension i) est une somme formelle de i-cellules. Dit autrement, c’est un ensemble pondéré de i-cellules, la pondération étant signée. À partir de ces i-chaînes est défini le groupe des chaînes Ci. L’opérateur de bord ∂ est défini pour chaque i-cellule c, i ∈ {1,…,n}, et donne une somme pondérée sur l’ensemble des (i−1)-cellules du bord de c. Le bord d’une i-chaîne est alors simplement la somme du bord de ses i-cellules (c’est une (i−1)-chaîne). Un cycle est une chaîne dont le bord est nul. Un bord est une i-chaîne qui est l’image d’une (i+1)-chaîne par l’opérateur de bord. L’ensemble des cycles (resp. bords) de dimension i de X est noté Zi(X) (resp. Bi(X)). La propriété principale de l’opérateur de bord est que pour toute chaîne c, c ∂ ∂ =0, c-à-d le bord d’une chaîne est nécessairement un cycle, qui donc n’a lui-même pas de bord. Deux chaînes c1 et c2 sont homologues si elles diffèrent par un bord. Dans ce cas, une chaîne peut s’écrire comme la somme de l’autre chaîne et d’un bord. La notion de chaîne homologue est une relation d’équivalence, et les groupes d’homologie sont définis par le quotient du groupe des cycles par cette relation d’équivalence. De ce fait, tout élément de Hi(X) est un cycle qui n’est pas un bord. Dit autrement, ∀ i ∈ {0,…,n}, le ième groupe d’homologie est noté Hi(X). Il est obtenu en quotientant le groupe des cycles par le sous-groupe des bords : Hi(X)=Zi(X)/Bi(X).
Les nombres de cellules d’une subdivision n’est pas un invariant topologique, mais sert au calcul des invariants topologiques numériques que sont la caractéristique d’Euler-Poincaré et les nombres de Betti.
Pour calculer ces nombres de cellules dans une carte (généralisée ou combinatoire), il suffit d’utiliser la définition de cellule, et pour chaque dimension de l’espace, de compter le nombre d’orbites distinctes. Cela donne un algorithme en O(n · k), où n la dimension de l’espace et k le nombre de brins de la carte. Mais lorsque ces nombres sont utilisés dans un algorithme itératif qui modifie la subdivision (comme dans l’application de segmentation avec contrôle topologique présentée Section 7.2), faire ce calcul à chaque étape de l’itération s’avère trop coûteux.
Pour régler ce problème, nous avons proposé un algorithme de mise à jour de ces nombres de cellules lors des opérations de suppression. Le principe de cet algorithme consiste à calculer une première fois les nombres de cellules (par exemple en utilisant la méthode comptant le nombre d’orbites) puis à les mettre à jour lors des opérations de suppression.
Lorsqu’une i-cellule est supprimée, cela modifie bien évidemment le nombre de i-cellules qui diminue de un, mais selon les configurations, d’autres modifications peuvent se produire :
Ces modifications possibles, qui ne sont pas exclusives, nous amènent à la Prop. 9 de mise à jour des nombres de cellules pour l’opération de suppression.
Il y a deux cas différents : le premier pour l’évolution du nombre de i-cellules qui diminue toujours de un, et le second pour tenir compte des trois types de modifications évoquées ci-dessus : fusions, disparitions, ou déconnexions de j-cellules, avec j ≠ i. La prise en compte correcte de ces trois cas nécessite de compter le nombre de j-cellules incidentes à c avant et après la suppression de c, le nombre de j-cellules étant alors simplement mis à jour en effectuant la différence entre ces deux nombres.
De ce fait, dans ces trois cas, la mise à jour du nombre de cellules va être correctement réalisée. (1) Si c séparait deux (i+1)-cellules distinctes qui sont fusionnées après la suppression, nous allons avoir e1=2 et e2=1, le nombre de (i+1)-cellules diminue de un (cf. l’exemple de la Fig. 6.2). (2) Si une j-cellule est incluse dans c, cette cellule va être comptée dans les cellules avant la suppression mais pas après et donc le nombre de j-cellules va bien diminuer de un (cf. l’exemple de la Fig. 6.4). (3) Si une j-cellule est déconnectée en trois j-cellules après la suppression, le nombre de j-cellules va augmenter de deux (cf. l’exemple de la Fig. 6.6).
Compter les nombres de cellules avant et après la suppression revient à compter des nombres d’orbites. Pour le nombre de j-cellules incidentes à c avant la suppression, nous avons directement e1=|{⟨h(αj)⟩(b)|b∈ c}|. Pour le nombre de j-cellules incidentes à c après la suppression, nous devons considérer les brins j-voisins de c qui n’appartiennent pas à c : vc=c αj∖ c. Ce sont les brins survivants «autour» de c. Le nombre de j-cellules incidentes à c après la suppression est alors e2=|{⟨h(αj)⟩(b)|b∈ vc}| en considérant la carte obtenue après l’opération de suppression.
Nous illustrons ces modifications dans différentes configurations. Tout d’abord, la Fig. 6.2 présente le cas général de la 2-suppression, lorsque la face supprimée est de degré deux, et qu’il n’existe pas d’arête uniquement incidente à cette face. La suppression de la face entraîne que le nombre de volumes diminue de un (deux volumes différents sont fusionnés), et que le nombre de faces diminue de un également (la face supprimée). La caractéristique d’Euler-Poincaré (qui est la somme alternée du nombre de cellules) est donc inchangée.
[a][b]
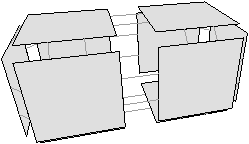
Figure 6.2: Cas général de 2-suppression d’une face de degré deux, sans arête uniquement incidente à cette face. (a) Carte initiale. La face à supprimer est en gris foncé. (b) Carte obtenue après la suppression de la face. Le nombre de volumes diminue de un (deux volumes différents sont fusionnés), et le nombre de faces diminue de un également : la caractéristique d’Euler-Poincaré est inchangée.
Dans la Fig. 6.3, la face supprimée f est de degré un et aucune de ses arêtes n’est incidente seulement à f. Le nombre de faces diminue de un et les autres nombres de cellules restent constants, ce qui entraîne la diminution de un de la caractéristique d’Euler-Poincaré. Il faut noter ici que la carte obtenue ne vérifie plus les conditions de la Def. 45 de caractéristique d’Euler cellulaire (page ??). De ce fait, cette caractéristique n’est plus valide, même si les nombres de cellules sont correct.
[a][b]
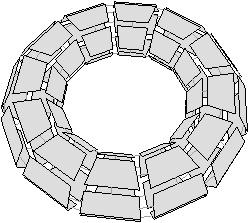
Figure 6.3: 2-suppression d’une face de degré un, sans arête uniquement incidente à cette face. (a) Carte initiale. La face à supprimer est en gris foncé. (b) Carte obtenue après la suppression de la face. Le nombre de faces diminue de un, les autres nombres de cellules restent constants : la caractéristique d’Euler-Poincaré diminue de un.
Dans l’exemple de la Fig. 6.4, la face supprimée f est de degré un, et trois de ses arêtes sont incidentes uniquement à f. Le nombre de faces diminue de un, le nombre d’arêtes diminue de trois, et le nombre de sommets diminue de deux. La caractéristique d’Euler-Poincaré est donc ici inchangée.
[a][b]
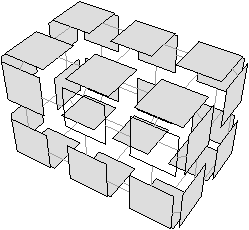
Figure 6.4: 2-suppression d’une face de degré un, ayant trois arêtes incidentes uniquement à la face supprimée. (a) Carte initiale (deux faces sont dessinées en fil-de-fer pour visualiser l’intérieur du volume). La face à supprimer est en gris foncé. (b) Carte obtenue après la suppression de la face, qui a entraîné la disparition des trois arêtes et des deux sommets incidents uniquement à cette face. Le nombre de faces diminue de un, le nombre d’arêtes de trois, et le nombre de sommets de deux : la caractéristique d’Euler-Poincaré est inchangée.
Dans l’exemple de la Fig. 6.5, la face supprimée f est de degré un, et deux de ses arêtes (non adjacentes1) sont incidentes uniquement à f. Le nombre de faces diminue de un, et le nombre d’arêtes diminue de deux : la caractéristique d’Euler-Poincaré augmente de un.
[a][b]
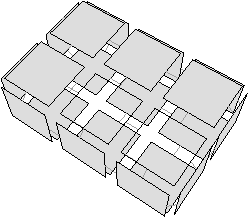
Figure 6.5: 2-suppression d’une face de degré un, ayant deux arêtes non adjacentes incidentes uniquement à la face supprimée. (a) Carte initiale (deux faces sont dessinées en fil-de-fer pour visualiser l’intérieur du volume). La face à supprimer est en gris foncé. (b) Carte obtenue après la suppression de la face, qui a entraîné la disparition des deux arêtes incidentes uniquement à cette face. Le nombre de faces diminue de un, et le nombre d’arêtes diminue de deux : la caractéristique d’Euler-Poincaré augmente de un.
Dans l’exemple de la Fig. 6.6, la carte initiale est composée d’un seul volume, car la face à supprimer f est reliée à elle-même par α2 le long de l’arête supérieure. Après la suppression de f, ce volume se trouve déconnecté en trois volumes distincts. Cela entraîne une diminution de un du nombre de faces et une augmentation de deux du nombre de volumes. Le nombre d’arêtes diminue également de un car une arête est incluse dans f.
[a][b]
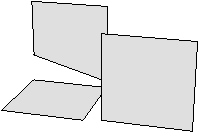
Figure 6.6: 2-suppression d’une face entraînant la déconnexion d’un volume en plusieurs volumes. (a) Carte initiale. La face à supprimer est en gris foncé. (b) Carte obtenue après la suppression de la face, qui a entraîné la déconnexion du volume en trois volumes. Le nombre de faces diminue de un, le nombre de volumes augmente de deux, et le nombre d’arête diminue de un.
Dans l’exemple de la Fig. 6.7, un volume incident à la face supprimée f est inclus dans f. La suppression de f entraîne la disparition de ce volume et donc le nombre de 3-cellules diminue de un. Comme le nombre de faces diminue également de un, la caractéristique d’Euler-Poincaré est inchangée.
[a][b]
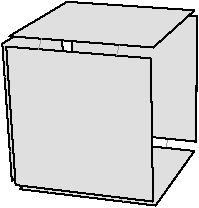
Figure 6.7: 2-suppression d’une face entraînant la disparition d’un volume. (a) Carte initiale. La face à supprimer est en gris foncé. (b) Carte obtenue après la suppression de la face, qui a entraîné la disparition du volume qui était incident uniquement à cette face. Le nombre de faces diminue de un, et le nombre de volumes diminue de un : la caractéristique d’Euler-Poincaré est inchangée.
Les deux exemples des Figs. 6.8 et 6.9 montrent l’évolution du nombre de cellules lors de la suppression d’arête. Dans le premier cas, le nombre de faces diminue de un (deux faces sont fusionnées), le nombre d’arêtes diminue de un et le nombre de sommets n’est pas modifié car les deux sommets de l’arête a ne sont pas incidents uniquement à a. La caractéristique d’Euler-Poincaré reste donc constante.
[a][b]
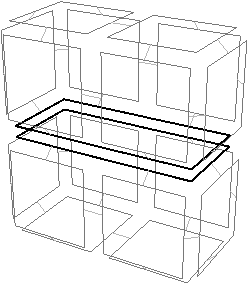
Figure 6.8: 1-suppression de l’arête incidente au brin b qui est de degré deux. (a) Carte initiale. (b) Carte obtenue après la suppression de l’arête qui a entraîné la fusion des deux faces en une. Le nombre de faces diminue de un, et le nombre d’arêtes aussi : la caractéristique d’Euler-Poincaré est inchangée.
Dans le second exemple de la Fig. 6.9, l’arête est pendante, donc un sommet est incident uniquement à l’arête. Le nombre de faces reste alors constant, le nombre d’arêtes diminue de un, et le nombre de sommets diminue également de un, ce qui fait que la caractéristique d’Euler-Poincaré reste également inchangée.
[a][b]
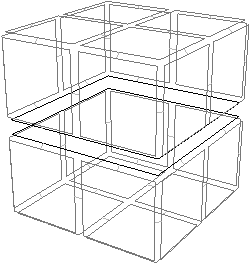
Figure 6.9: 1-suppression de l’arête incidente au brin b qui est pendante. (a) Carte initiale. (b) Carte obtenue après la suppression de l’arête qui a entraîné la disparition du sommet incident uniquement à cette arête. Le nombre d’arêtes diminue de un, et le nombre de sommets aussi : la caractéristique d’Euler-Poincaré est inchangée.
Cette mise à jour nécessite donc le parcours des j-cellules incidentes à c, afin de compter leur nombres avant et après la suppression. Même si dans le pire des cas toutes les cellules de la carte sont incidentes à c, il est clair que dans la majorité des cas le nombre de cellules à tester sera petit en comparaison du nombre de brins de la carte car cela reste un traitement local.
Ces modifications des nombres de cellules de la subdivision nous donnent directement un algorithme permettant de calculer la caractéristique d’Euler-Poincaré lors des opérations de suppression, sous réserve que la carte vérifie les conditions de la caractéristique d’Euler cellulaire. De plus, en utilisant la dualité suppression/contraction, la Prop. 9 s’étend directement aux opérations de contraction :
Enfin, il est possible d’utiliser ce principe de mise à jour du nombre de cellules pour stocker et mettre à jour le nombre de cellules de chaque région d’une carte.
Une région R est un élément de dimension n, ayant un bord externe (une quasi variété de dimension n−1) et k bords internes entourant les cavités de R (k quasi-variétés). Une région sans cavité (k=0) est équivalente à une n-cellule, mais ce n’est pas vrai pour les régions avec cavités (cf. le chapitre 4 où nous avons utilisé cette notion de région dans le cadre cartes topologiques).
Nous associons alors à chaque région son nombre initial de cellules, puis mettons à jour ces nombres lors des opérations de suppression (cela nous servira Section 6.3 pour le calcul des nombres de Betti des régions).
Cela entraîne deux types de changements par rapport à ce que nous venons de présenter, où les cellules étaient comptées de manière globale à toute la carte, alors qu’elles sont maintenant comptées indépendamment pour chaque région :
Pour la (n−1)-suppression d’une cellule c, il y a deux cas différents selon si c est incidente à deux régions distinctes ou à une seule région (cf. Prop. 11).
Dans le premier cas, nous devons calculer le nombre de cellules de la nouvelle région qui est la fusion des deux régions initiales. Pour cela, nous commençons par additionner les nombres de cellules de R1 et de R2. Mais certaines cellules peuvent alors être comptées deux fois : ce sont les cellules qui étaient incidentes aux deux régions R1 et R2. Pour chacune de ces i-cellules, le nombre de i-cellules de la région résultante est diminuée de un ce qui fait que la cellule est désormais bien comptée une seule fois. Il ne reste plus qu’à utiliser la propriété précédente de mise à jour des nombres de cellules pour l’opération de suppression (donnée Prop. 9) sur la région résultante pour tenir compte des modifications entraînées par la (n−1)-suppression de c. Dans le cas où la cellule supprimée est incidente à une seule région R, la modification est plus simple puisqu’il suffit alors d’utiliser directement la Prop. 9 car il n’y a alors pas de fusion de régions.
Pour les autres opérations, que ce soit la i-suppression, avec 0≤ i<n−1, ou la i-contraction, avec 1≤ i≤ n, les Props. 9 et 10 sont toujours valides, mais elles doivent êtres appliquées pour chaque région incidente à la cellule concernée. Par exemple la suppression d’une arête en 3D va modifier le nombre de cellules de toutes les régions autour de cette arête. Cette modification se fait simplement en parcourant l’orbite de la cellule supprimée ou contractée, et en appliquant la définition correspondante pour chaque nouvelle région rencontrée.
Nous avons utilisé ces propriétés de mise à jour des nombres de cellules de chaque région lors des opérations de suppression dans [DPFL06] pour compter ces nombres durant l’extraction de la carte topologique 3D. Comme cette extraction s’effectue par un balayage de l’image voxel par voxel, nous avons pu éviter le premier calcul global des nombres de cellules en initialisant ces nombres lors de la création de nouvelles régions. En effet, une région est toujours initialement associée à un seul voxel et nous pouvons donc fixer ses nombres de volumes, faces, arêtes et sommets à un, six, douze et huit. Nous utilisons ensuite les formules données ci-dessus pour mettre à jour ces nombres de cellules lors des opérations de suppression. Nous avons pu simplifier, et donc optimiser, la mise à jour des nombres de cellules en utilisant les propriétés spécifiques liées aux propriétés de la carte topologique et de l’algorithme d’extraction. À la fin de l’extraction de la carte topologique, nous avons directement les nombres de cellules de chaque région, avec un surcoût presque nul par rapport à l’algorithme initial (cf. [DPFL06] pour plus de détails). Ces nombres nous servent ensuite à calculer la caractéristique d’Euler-Poincaré, soit de la subdivision globale, soit de chaque région. Nous avons également utilisé ces nombres comme outils de base pour calculer les nombres de Betti.
De manière similaire au calcul de la caractéristique d’Euler-Poincaré, nous avons proposé deux méthodes permettant de calculer les nombres de Betti d’une région dans une carte (combinatoire ou généralisée) : une méthode directe, et une seconde méthode utilisant les opérations de suppression et la mise à jour locale des nombres de cellules. Ce travail est pour le moment limité aux objets 3D orientables, et une perspective est son extension à tout type de quasi-variété. Par contre, il est valide pour les cartes combinatoires et les cartes généralisées car il se base sur les nombres de cellules qui sont définis pour les deux modèles. Ce travail est un résultat de la thèse d’Alexandre Dupas [Dup09] et a été présenté dans [DD09].
Pour calculer les nombres de Betti d’une région R donnée, nous utilisons les propriétés présentées à la section précédente permettant de calculer le nombre de cellules de chaque région d’une carte. Nous notons χ′(R) la somme alternée (le nombre sommets moins le nombre d’arêtes plus le nombre de faces) des cellules de la région R. Ce nombre n’est pas la caractéristique d’Euler-Poincaré de la région R dans le cas où elle possède des cavités ou des tunnels (car la région n’est alors pas homéomorphe à une boule, donc la carte n’est pas un complexe cellulaire). Mais nous allons voir dans ce chapitre que ce nombre peut être utilisé pour calculer la caractéristique d’Euler-Poincaré et donc les nombres de Betti.
La première méthode permettant de calculer les nombres de Betti consiste à utiliser directement χ′(R), et le nombre de surfaces bordant la région R. Comme nous ne considérons ici que des objets 3D orientables plongés dans ℝ3, seuls les trois premiers nombres de Betti sont significatifs (b0, b1 et b2), les autres étant tous nuls.
b0(R) est toujours égal à un car il compte le nombre de composantes connexes de l’objet, et nous calculons le nombre de Betti d’une région qui est connexe par définition (un objet non connexe à nécessairement plusieurs bords externes).
Nous étudions maintenant b2, car nous verrons par la suite que b1 se déduit des autres nombres. b2(R) compte le nombre de cavités de la région R. Ce nombre est égal au nombre de surfaces bordant R, noté #s(R), moins un. En effet, le bord de chaque région est composé d’une surface externe, et de k surfaces internes, une par cavité de la région. Pour calculer #s(R), nous devons retrouver toutes les surfaces bordant la région R. Cette information n’est pas contenue dans la carte, et il est nécessaire d’avoir une structure de données supplémentaire la représentant. Nous avons présenté au chapitre 4 l’arbre d’imbrication des régions qui est une réponse à ce besoin, et que nous réutilisons ici. L’avantage de cet arbre est que les régions imbriquées sont regroupées par composantes connexes. De ce fait, chaque région R a pour fils direct un représentant par composante connexe, et donc le nombre de surfaces internes de la région est exactement le nombre de ses fils directs, noté fils(R).
Il reste à étudier b1(R) qui compte le nombre de tunnels de la région R. Ce nombre est lié à la caractéristique d’Euler-Poincaré par la formule χ(R)=b0(R)−b1(R)+b2(R) (cf. Def. 14). Notre démarche consiste ici à calculer χ(R). Comme nous venons de donner les formules permettant de calculer b0(R) et b2(R), cela nous permettra directement de calculer b1(R).
Nous avons vu au chapitre précédent comment calculer χ′(R), mais ce nombre peut être différent de la caractéristique d’Euler-Poincaré. Ce cas se pose lorsque la carte n’est pas un complexe cellulaire (au sens présenté au chapitre 2), c’est-à-dire si toutes ses cellules ne sont pas homéomorphes à des boules. Nous nous plaçons ici dans un cadre similaire à celui utilisé pour la carte topologique dans lequel chaque 0-cellule, 1-cellule et 2-cellule est homéomorphe à une boule, et seuls les volumes ne sont pas nécessairement des boules. Cette supposition est raisonnable pour deux raisons. Premièrement elle est toujours vraie pour les 0-cellules et les 1-cellules. Deuxièmement, le cas d’une 2-cellule non homéomorphe à une boule pose des difficultés dans la manipulation des faces. Ces problèmes sont résolus en conservant des arêtes fictives lors des opérations de suppression, ce qui préserve alors chaque face homéomorphe à une 2-boule (cf. chapitre 4).
Notre solution afin de traiter correctement le cas des régions non homéomorphes à des boules consiste à rajouter des cellules pour rendre ces régions homéomorphes à des boules, et pour lesquelles nous avons alors χ′(R)=χ(R). En pratique, ces éléments ne sont pas ajoutés dans la carte mais simplement comptés comme s’ils étaient présents : c’est la notion de cellules implicites.
La Fig. 6.10 présente deux exemples de cellules implicites. La région de la Fig. 6.3.1 contient un tunnel qui est bouché par la face implicite dessinée en gris : l’objet devient homéomorphe à une 3-boule. Dans la Fig. 6.3.1, la région contient une cavité, qui est reliée à la surface externe par une face implicite (en gris sur la figure), ce qui rend le volume de la région homéomorphe à une 3-boule. Cette face est composée de 4 arêtes, les deux arêtes noires qui existaient déjà sur les deux surfaces à relier, et les deux autres en gris qui sont des nouvelles arêtes implicites.
[a][b]
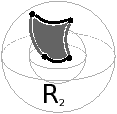
Figure 6.10: Exemples de cellules implicites (dessinées en gris foncé) pour des régions qui ne sont pas homéomorphes à des 3-boules. (a) Une région torique R1. La face implicite permet de couper le tunnel en deux et ainsi rend la région homéomorphe à une 3-boule. (b) Une région sphérique R2 ayant une cavité sphérique. L’ajout de la face implicite permet de connecter la cavité avec l’extérieur et ainsi rend la région homéomorphe à une 3-boule.
Nous pouvons maintenant utiliser ces cellules implicites pour lier χ(R) et χ′(R). En effet, χ′(R) est la somme alternée du nombre de cellules des surfaces bordant R : χ′(R)=#c0(R)−#c1(R)+#c2(R). La caractéristique d’Euler-Poincaré χ(R) est quant à elle la somme alternée du nombre de cellules du complexe cellulaire χ(R)=k0(R)−k1(R)+k2(R)−k3(R), en notant ki(R) le nombre de i-cellules du complexe cellulaire associé à la région R, en tenant compte des cellules implicites.
Il suffit d’utiliser la Def. 83 donnant les cellules implicites qui sont ajoutées pour faire le lien entre les ki(R) et les #ci(R). k0(R)=#c0(R) car il n’y a pas de sommet implicite. k1(R)=#c1(R)+2 b2(R) car il y a deux arêtes implicites ajoutées pour chaque cavité de R, et ce nombre de cavités est b2(R). Enfin, k2(R)=#c2(R)+b1(R)+b2(R) car il y a une face ajoutée pour chaque tunnel et une face ajoutée pour chaque cavité. k3(R)=1 car chaque région est connexe, donc composée d’un seul volume par définition.
En remplaçant les ki(R) par ces nouvelles écritures, nous obtenons χ(R)=(#c0(R)−#c1(R)+#c2(R))−(1−b1(R)+b2(R)). Comme χ(R)=1−b1(R)+b2(R) (cf. la Def. 14 page ?? liant les nombres de Betti et la caractéristique d’Euler-Poincaré), nous avons directement χ(R)=χ′(R)/2.
En re-écrivant la formule χ(R)=b0(R)−b1(R)+b2(R) pour calculer b1(R), nous obtenons b1(R) = b0(R) + b2(R) − χ′(R) / 2. Nous avons montré à la section précédente comment calculer χ′(R), et nous venons de voir comment calculer b0(R) et b2(R), nous pouvons donc à l’aide de cette formule calculer b1(R).
Pour résumer, les nombres de Betti d’une région R sont donnés par la proposition suivante :
Pour utiliser les nombres de Betti au sein d’algorithmes modifiant une carte à l’aide des opérations de suppression, nous avons défini une méthode de mise à jour locale de ces nombres de Betti.
Comme b0(R) est égal à 1 pour toute région R, il n’y a pas de mise à jour à réaliser.
Pour calculer b1(R), nous venons de donner une formule basée sur b0(R), b2(R) et χ′(R). Nous avons vu au chapitre précédent comment mettre à jour localement χ′(R), et b0(R) est constant. En donnant la manière de mettre à jour localement b2(R), nous serons donc directement capables de mettre à jour b1(R).
Étudions donc maintenant la mise à jour de b2(R) qui est le nombre de cavités de la région R. La mise à jour locale consiste donc à étudier les évolutions du nombre de cavités de R durant les opérations de suppression. Nous pouvons faire une première remarque qui est que le nombre de cavités est constant lors des 0-suppressions et des 1-suppressions d’une cellule non isolée et n’entraînant pas de déconnexion de cellule. En effet, ce type de suppression ne peut pas entraîner de création ou de suppression de cavités. Nous nous intéressons donc uniquement à l’opération de 2-suppression. Nous avons vu au chapitre précédent que le nombre de cavité est égal au nombre de surfaces bordant R (noté #s(R)) moins un (pour ne pas compter la surface externe). Nous étudions donc comment calculer #s(R), ce qui nous donnera directement b2(R).
Nous étudions pour cela l’impact de la suppression d’une 2-cellule c sur le nombre de surfaces bordant la région R. Nous pouvons remarquer que seules les surfaces incidentes à c sont concernées par la suppression. Comme pour les 0- et 1-suppressions, nous ajoutons une contrainte sur la 2-cellule à supprimer qui ne doit pas être isolée2. Dans ce cas, la suppression de la cellule peut soit ne pas modifier le nombre de surfaces, soit l’augmenter, mais en aucun cas le diminuer. En effet, une 2-suppression de cellule non isolée peut éventuellement déconnecter une surface en plusieurs parties (et donc augmenter le nombre de surfaces) mais ne peut pas fusionner plusieurs surfaces en une seule.
Comme pour la mise à jour locale du nombre de cellules, nous distinguons deux cas selon le type de la 2-cellule supprimée. Si c sépare deux régions distinctes R1 et R2, il y a deux surfaces incidentes à c avant la suppression (une du côté de R1 et une autre du coté de R2), et ces deux surfaces sont fusionnées en une seule après la suppression. De ce fait, le nombre de surfaces de la nouvelle région #s(R1∪ R2)=#s(R1)+#s(R2)−1 (comme ∀ R, #s(R)>0, #s(R1∪ R2)>#s(R1) et #s(R1∪ R2)>#s(R2)).
Si c est incidente à une seule région R, la mise à jour est plus complexe car nous devons tester quelles surfaces incidentes à c sont déconnectées, en étudiant le nombre de composantes connexes de l’orbite ⟨α0,α1,α2⟩ autour de c, avant et après la suppression (de manière similaire à la mise à jour locale du nombre de cellules présenté à la section précédente).
Nous proposons pour cela un algorithme qui calcule le nombre de surfaces incidentes à c qui seront disjointes après la suppression de c. Cet algorithme permet de calculer les nombres de Betti de l’union de deux régions avant de réaliser cette union, ce qui est utile dans les algorithmes souhaitant contrôler l’évolution des caractéristiques topologiques (cf. l’application de segmentation avec contrôle topologique présentée au chapitre 7).
Nous utilisons pour cela l’Algorithme 6.3.2 qui parcourt une surface, sans passer par des faces marquées .
Figure 6.11: Algorithme : Parcours de la surface en sautant les face marquées
- Entrées : Une carte combinatoire C ;
Un brin b non marqué minner ;
Une marque minner marquant les faces à ignorer.- Résultat : Parcours de la surface incidente à b en ignorant les faces marquées.
P ← pile de brins vide;
empiler b dans P;
Tant que P n’est pas vide faire
b′ ← tête de P;
dépiler P;
Si b′ n’est pas déjà traité alors
// le brin b′ appartient à la surface incidente à b
// traiter le brin
empiler β1(b′) dans P;
b2 ← β2(b′);
Tant que b2 est marqué par minner faire
b2 ← β32(b2);
empiler b2 dans P;
Le principe de cet algorithme est similaire à un parcours classique de surface. Il utilise une pile des brins à traiter, et pour un brin non traité va ajouter dans la pile les voisins de ce brin par β1 et β2. Le changement par rapport à un parcours classique de surface consiste à ne pas empiler directement le brin β2(b′) mais à sauter les éventuelles faces marquées en utilisant β32 autant de fois que nécessaire jusqu’à obtenir un brin non marqué par minner. Cela revient à simuler l’opération de 2-suppression qui redéfinit β2 de cette manière. De ce fait, la surface parcourue par cet algorithme est identique à la surface qui serait parcourue après la suppression des faces marquées minner. Cet algorithme est donné pour un ensemble quelconque de faces marquées, de manière similaire à la définition de l’opération de suppression d’un ensemble de cellules. De plus, nous l’avons donné ici pour les cartes combinatoires mais il peut être porté très simplement pour les cartes généralisées, la seule différence étant qu’il faudra parcourir α0, α1 et α2 pour parcourir la surface, et utiliser α32 pour sauter les faces marquées.
Cet algorithme de parcours de surface en sautant les faces marquées est la base de l’Algorithme 6.3.2 qui va calculer le nombre de surfaces incidentes à une 2-cellule c qui seront disjointes après la suppression de c.
Figure 6.12: Algorithme : Compte les surfaces autour d’une face après sa suppression.
- Entrées : Une carte combinatoire C ;
Un brin b.- Résultat : Le nombre de surfaces incidentes à c2(b) après la suppression de c2(b).
k ← 0;
minner, mtraite ← marques sur les brins;
marquer tout les brins de c2(b) avec minner;
Pour chaque brin d ∈ c2(b) faire
Si β2(d) n’est pas marqué par mtraite ni par minner alors
marquer avec mtraite la surface incidente à β2(d) en sautant les brins marqués par minner;
k ← k+1;
Retourner k;
Le principe de cet algorithme consiste tout d’abord à marquer avec la marque minner tous les brins de la cellule c2(b) qui va être supprimée. Ensuite, pour chaque brin de cette cellule, nous testons si le brin β2(d) n’est pas un brin déjà traité ni un brin de c2(b). En effet, dans le premier cas, sa surface a déjà été comptée, et dans le deuxième cas c’est qu’il n’y a pas de surface incidente à ce brin. Lorsque ces deux conditions sont vérifiées, la surface incidente à ce brin est marquée avec mtraite, en sautant les brins marqués minner (ce qui garantit que la surface traitée ne passe pas par la cellule c2(b)). Nous avons trouvé une nouvelle surface, et incrémentons donc le résultat de un, puis passons à un autre brin. À la fin de cet algorithme, nous avons parcouru toutes les surfaces incidentes à c2(b), et nous avons donc compté toutes les futures surfaces distinctes que nous allons obtenir après la suppression de c2(b).
Cet algorithme a une complexité linéaire en nombre de brins des surfaces incidentes à c2(b). C’est une complexité importante pour une mise à jour, mais elle reste locale en nombre de brins des cellules incidentes à la cellule supprimée.
Le nombre de surfaces de R après la suppression de c2(b) se calcule maintenant très simplement : #s(R)=#s(R)−1+k, où k est le nombre de surfaces autour de c2(b) (le résultat de l’Algorithme 6.3.2). Nous enlevons un pour enlever la surface initiale qui était incidente à c2(b), car cette surface sera comptée dans l’algorithme. Comme c2(b) n’est pas isolée, k>0 et donc nécéssairement #s(R) est inchangé ou augmente.
Nous pouvons maintenant résumer la mise à jour locale du nombre de surfaces pour la 2-suppression de la cellule c2(b) :
Cela nous donne directement la mise à jour locale de b2(R) puisqu’il est égal à #s(R)−1.
Après les nombres de Betti, nous nous intéressés à un autre invariant topologique : le schéma polygonal canonique. Après avoir étudié cet invariant, nous avons remarqué que nous obtenons le même type de résultats que ceux présentés chapitre 4 pour la carte topologique 3D, dans le cas des régions représentées par une surface fermée. Cela nous a amenés à étudier le lien entre les opérations que nous utilisons lors de la construction de cette carte topologique (les opérations de suppression et le décalage d’arête) et les opérations utilisées pour la construction du schéma polygonal canonique : ces opérations sont basées sur la découpe et le collage de la surface, et la transcription de ces opérations en terme de transformations de mots. Nous avons ainsi pu transcrire l’algorithme original [VY90] qui transforme un schéma polygonal en schéma polygonal canonique dans un algorithme effectuant la transformation similaire pour une 2G-carte [DA08].
Le premier algorithme permettant de construire un schéma polygonal canonique provient de [VY90]. Dans cet article, les auteurs définissent 5 règles de transformation, ils prouvent que ces règles préservent la topologie de la surface, et que l’application itérative de ces règles permet toujours d’obtenir le schéma polygonal canonique.
L’algorithme se décompose en deux étapes. La première consiste à transformer le schéma polygonal initial en un schéma polygonal réduit, c’est-à-dire un polygone de la forme aa dans le cas de la sphère, ou un polygone dont la subdivision de la surface associée est composée d’un seul sommet. Cette première étape est réalisée à l’aide des deux transformations A et B suivantes :
[a][b]
[c]
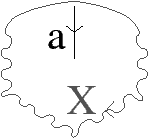
Figure 6.13: Transformation A : aaX ⇒ X. (a) Le schéma polygonal initial. (b) Les deux arêtes a sont identifiées. (c) L’arête a est effacée, car elle est à l’intérieur du polygone.
(où X et Y sont des mots quelconques, éventuellement vides).
La transformation B est découpée en deux cas selon que l’arête a est orientable3 ou non. Ces trois cas sont illustrés dans les Figs. 6.13, 6.14 et 6.15.
[a][b]
[c]
[d]
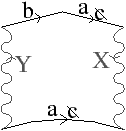
Figure 6.14: Transformation B dans le cas orientable : aXabY ⇒ baXaY. (a) Le schéma polygonal initial. (b) Le polygone est coupé pour isoler les arêtes a et b. (c) Le morceau coupé est re-collé le long de l’arête a. (d) L’arête a est effacée, car elle est à l’intérieur du polygone, et l’arête c est renommée a.
[a][b]
[c]
[d]
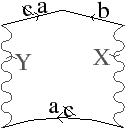
Figure 6.15: Transformation B dans le cas non-orientable : aXabY ⇒ abXaY. Les étapes sont les mêmes que dans le cas orientable, mais le résultat change de par le fait que l’arête a est non-orientable.
En utilisant ces transformations de manière itérative, un algorithme linéaire permet de transformer n’importe quel schéma polygonal en schéma polygonal réduit [VY90].
La deuxième étape de la transformation consiste à transformer ce schéma réduit en schéma polygonal canonique. Pour cela, les trois transformations C, D et E sont utilisées :
(où X et Y sont à nouveau des mots quelconques, éventuellement vides). Ces trois transformations peuvent, comme les deux précédentes, être réalisées sur le schéma polygonal par des opérations de découpe et de collage (cf. [VY90]).
Nous nous intéressons maintenant à la manière de construire le schéma polygonal d’une 2G-carte fermée, où chaque arête est représentée par quatre brins. La première étape consiste à étiqueter chaque brin de la G-carte. Pour chaque brin b n’ayant pas encore d’étiquette, nous l’étiquetons avec une nouvelle étiquette e, étiquetons le brin α2(b) avec e, et enfin nous étiquetons les deux brins α0(b) et α02(b) avec l’étiquette inverse e. L’arête incidente au brin b est donc associée à l’étiquette e, et les deux orientations possibles de l’arête ont bien des étiquettes inverses (cf. exemple de la Fig. 6.4.2).
[a][b]
[c]
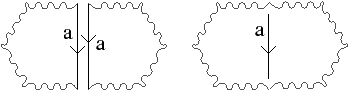
Figure 6.16: (a) Une 2G-carte ayant ses brins étiquetés : deux brins en relation par α0 ont deux étiquettes inverses, et deux brins en relation par α2 ont même étiquette. (b) 2G-carte où l’arête a a été supprimée. Le mot associé est W=dbcdcb. (c) L’opération correspondante pour obtenir un schéma polygonal consiste à coller les deux polygones le long des arêtes a et à supprimer l’arête a.
Pour construire le schéma polygonal, cette carte doit être simplifiée afin de ne contenir qu’une seule face qui est le polygone. Pour cela, chaque arête de degré 2 de la carte est supprimée. Comme nous pouvons voir Fig. 6.16, cette opération est équivalente à coller deux polygones le long d’une arête de même étiquette puis à effacer cette arête. Comme chaque arête de degré deux est supprimée, et comme la 2G-carte initiale est fermée, à la fin de cette étape la G-carte est composée d’une seule face car toutes les arêtes restantes sont de degré un (donc incidentes deux fois à la même face).
Le mot associé à cette 2G-carte et représentant le schéma polygonal est calculé en partant d’un brin b quelconque de cette carte. L’étiquette de b donne la première lettre du mot. Ensuite, la carte est parcourue en déplaçant b sur le brin α01(b), et en ajoutant la lettre obtenue à la fin du mot. Le mot est terminé lorsque b est revenu sur le brin initial (cf. Fig. 6.4.2).
Nous avons maintenant une 2G-carte composée d’une seule face, mais ayant plusieurs arêtes et sommets. La première étape de l’algorithme initial consiste à transformer ce polygone en un polygone réduit, c-à-d un polygone équivalent mais n’ayant plus qu’un seul sommet.
Nous utilisons pour cela les deux transformations A et B de l’algorithme original, en les transposant aux 2G-cartes. Pour la transformation A, le mot est de la forme aaX. Dans ce cas, l’arête a est pendante et la transformation revient à supprimer cette arête pendante (cf. Fig. 6.17).
[a][b]
[c]
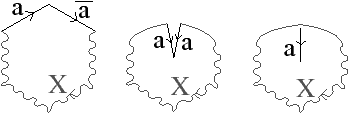
Figure 6.17: Transformation A. (a) Une 2G-carte avec une arête pendante a. (b) La 2G-carte obtenue après la suppression de l’arête a. (c) L’opération correspondante sur le schéma polygonal.
La transformation B correspond à l’opération de décalage d’arête. Nous avons exactement le même résultat que sur le polygone : l’opération utilisée est identique dans le cas orientable et le cas non-orientable, mais elle produit deux résultats différents.
Pour la transformation B dans le cas ou l’arête a est orientable (c-à-d prise deux fois dans des sens opposés), le mot associé est aXabY (avec éventuellement X ou/et Y vide). Après le décalage de l’arête a, le mot devient baXaY : la lettre qui était après a a été mise avant a (cf. Fig. 6.18).
(a) (c) (e) 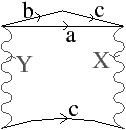
(b) (d) (f)
Figure 6.18: Transformation B dans le cas orientable. (a) Une 2G-carte avec une arête orientable a. (b) Le schéma polygonal correspondant. (c) et (d) première étape : une nouvelle arête est insérée, c, qui va couper le polygone en isolant les arêtes a et b. (e) et (f) deuxième étape : l’arête a est supprimée, en deux temps dans le schéma polygonal, puis l’arête c est renommée a.
Pour la transformation B dans le cas ou l’arête a est non-orientable (c-à-d prise deux fois dans le même sens), le mot associé est aXabY (avec éventuellement X ou/et Y vide). Après le décalage de l’arête a, le mot devient abXaY : la lettre qui était après le second a est inversée et mise après le premier a (cf. Fig. 6.19).
(a) (c) (e) 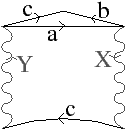
(b) (d) (f)
Figure 6.19: Transformation B dans le cas non-orientable. (a) Une 2G-carte avec une arête non-orientable a. (b),(c), (d), (e) et (f) sont les mêmes étapes que pour le cas orientable.
Pour transformer le schéma polygonal réduit en schéma polygonal canonique, les trois opérations C, D et E sont utilisées.
La transformation C transforme le mot aXaY en aaY−1X, avec a une arête non-orientable. Cette transformation peut être réalisée en décalant |Y| fois l’arête a. En effet, le mot initial peut s’écrire sous la forme aXay1… yk (les yi étant les lettres du mot Y). Nous venons de voir (pour la transformation B2) que lors du décalage d’une arête non-orientable, la lettre qui était après le second a est inversée et mise après le premier a. De ce fait, décaler l’arête a une fois va nous donner le mot ay1Xay2… yk. Le second décalage va donner le mot ay2y1Xay3… yk et ainsi de suite jusqu’à obtenir le mot aayk…y1X qui correspond bien à aY−1Xa. Le problème de cette transformation est que l’algorithme associé a une complexité en O(k), avec k le nombre de lettres du polygone.
Nous avons donc proposé un algorithme optimisé (cf. l’Algorithme 6.4.4 et Fig. 6.21) qui va effectuer la transformation C sur la 2G-carte en O(1).
1-coudre(α01(a),α201(a));
1-coudre(α1(a),α0(a));
1-coudre(a,α20(a));
Figure 6.20: Algorithme : Transformation C(a)
(a) (b)
Figure 6.21: Transformation C. (a) Une 2G-carte correspondant au mot aXaY. (b) La 2G-carte obtenue comme résultat de l’Algorithme 6.4.4 : elle correspond bien au mot aaY−1X.
Nous pouvons vérifier sur la Fig. 6.21 que l’algorithme correspond bien à la transformation C. Cet algorithme a une complexité en temps constant car il est composé d’opérations atomiques de liaison de brins qui s’effectuent en temps constant, et ce quel que soit la longueur du mot Y, ce qui n’est a priori pas évident étant donné qu’il faut inverser l’ordre et la valeur des lettres de ce mot. Mais ces transformations se font directement grâce au fait qu’une 2G-carte contient les deux orientations possibles de chaque chemin et donc de chaque mot. De ce fait, changer simplement le point d’entrée dans le mot Y revient à inverser l’ordre et la valeur des lettres (cf. Fig. 6.22).
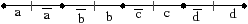
Figure 6.22: Exemple d’inversion d’un mot représenté dans une G-carte. Si le premier brin rencontré est celui étiqueté a, le mot est Y=abcd. En commençant le parcours par le dernier brin de ce chemin, étiqueté d, le mot est dcba, qui est bien égal à Y−1.
La transformation D peut, comme la C, s’effectuer de manière non optimisée en décalant plusieurs fois l’arête a et l’arête b. Mais nous pouvons également définir un algorithme optimisé, donné Algorithme 6.23 et illustré Fig. 6.24, qui effectue la modification en temps constant.
1-coudre(α1(a),α21(a));
1-coudre(α1(b),α21(b));
1-coudre(a,α201(a));
1-coudre(α01(b),α201(b));
1-coudre(α2(b),α01(a));
1-coudre(α2(a),α02(b));
1-coudre(b,α0(a));
1-coudre(α20(a),α0(b));
Figure 6.23: Algorithme : Transformation D(a,b)
(a) (b)
Figure 6.24: Transformation D. (a) Une 2G-carte correspondant au mot aXbYaUbV. (b) La 2G-carte obtenue comme résultat de Algorithme 6.23 : elle correspond bien au mot ababXVUY.
Enfin, de manière similaire, nous proposons un algorithme optimisé pour la transformation E (Algorithme 6.25 et Fig. 6.26) qui est à nouveau en O(1).
1-coudre(α0(a),α2(a));
1-coudre(α02(a),b);
1-coudre(α0(b),α2(b));
1-coudre(α02(b),c);
Figure 6.25: Algorithme : Transformation E(a,b,c)
(a) (b)
Figure 6.26: Transformation E. (a) Une 2G-carte correspondant au mot ababccX. (b) La 2G-carte obtenue comme résultat de Algorithme 6.25 : elle correspond bien au mot aabbccX.
Nous avons donc désormais tous les outils nécessaires pour calculer le schéma polygonal canonique de n’importe quelle 2G-carte fermée. Ces outils sont les briques de base utilisées dans l’algorithme original, ce qui nous donne directement notre algorithme sur les 2G-cartes. L’avantage de notre approche par rapport à la méthode initiale est que nous travaillons directement sur la subdivision et pas sur un mot associé (bien qu’il soit directement possible de retrouver ce mot). Cela évite une étape préalable de transformation de la surface, et cela permet surtout de faire le lien plus directement entre les transformations utilisées et les modifications de la surface sous-jacente. Nous souhaitons par exemple étudier comment mettre à jour la géométrie de la surface afin de pouvoir dessiner le polygone canonique sur la surface initiale, et cela sera plus simple avec notre approche qui modifie directement la subdivision qu’avec la méthode originale qui travaille sur le mot correspondant. Un autre avantage de notre approche est la transformation C que nous pouvons réaliser en O(1) et ce sans aucune structure de données annexe, chose qui n’est pas possible dans l’algorithme initial. Un autre point de recherche qu’il serait intéressant d’étudier est l’extension en 3D de la notion de schéma polygonal. En effet, la notion de schéma polyédrique a été introduite par Poincaré dans les années 1895 [Sti80], mais apparemment il y a eu très peu de travaux autour de cette notion. Avec les cartes, nous avons les outils nécessaires pour représenter et manipuler les subdivisions 3D, et cela pourrait servir de pont vers la meilleure compréhension et vers l’extension possible du schéma polygonal en 3D.
Après avoir étudié les invariants topologiques numériques que sont la caractéristique d’Euler-Poincaré et les nombres de Betti, et un invariant non numérique mais limité aux surfaces, le schéma polygonal canonique, l’étape suivante était d’étudier les groupes d’homologie. Afin d’attaquer ce problème de manière progressive, nous l’avons tout d’abord étudié en 2D dans le cas des surfaces fermées, orientables ou non [DPF06], puis nous avons étendu ce premier travail aux subdivisions orientables 3D [DPF08]. La généralisation en nD de ces travaux est en cours de réalisation.
Pour calculer les groupes d’homologie d’une 2G-carte, le principe est similaire au calcul du schéma polygonal réduit de la section précédente. Il consiste à simplifier une 2G-carte fermée, qui représente donc une surface, dans une représentation minimale tout en préservant son homologie. L’ensemble des arêtes de la 2G-carte minimale obtenue est l’ensemble des générateurs du premier groupe d’homologie de la surface initiale. L’approche utilisée est similaire à l’algorithme présenté dans [KMS98]. Mais la méthode présentée dans ce papier peut ne pas aboutir à une représentation minimale. Nous résolvons ce problème par l’utilisation de l’opération de décalage d’arête qui garantit, comme nous avons vu dans la section précédente, que l’objet obtenu soit minimal. La principale différence avec le schéma polygonal est que nous n’obtenons pas de représentation canonique mais nous limitons à l’équivalent du schéma polygonal réduit.
Le principe de la méthode présentée Algorithme 6.27 est de commencer par supprimer les arêtes de degré deux et les arêtes pendantes jusqu’à obtenir une 2G-carte composée d’une seule face, puis par supprimer les sommets de degré deux, en utilisant au préalable le décalage d’arête, jusqu’à obtenir une 2G-carte composée d’un seul sommet (le nombre d’arêtes étant alors fixé par la caractéristique d’Euler-Poincaré de la surface).
- Entrées : Une 2G-carte G fermée.
- Résultat : La simplification de G dans sa forme minimale.
1.
Pour chaque arête a de G faire
Si a est de degré 2 alors
Supprimer a;
Sinon Tant que a est une arête pendante faire
a′ ← une arête adjacente à a;
Supprimer a; a ← a′;
2.
Pour chaque sommet s de G faire
Si s est de degré 2 alors
Supprimer s;
Sinon Si il existe une arête a non-boucle incidente à s alors
Décaler toutes les arêtes incidentes à s sauf a;
Supprimer s;
Figure 6.27: Algorithme : Simplification d’une 2G-carte dans sa forme minimale.
Lors de la première étape de l’algorithme, les arêtes sont supprimées dans n’importe quel ordre. Pour les arêtes de degré deux, deux faces distinctes sont fusionnées. Les autres arêtes sont de degré un. Les arêtes pendantes doivent être supprimées, et les autres doivent être conservées car leur suppression entraînerait la déconnexion d’une face.
Lorsqu’une arête pendante a est supprimée, nous devons éventuellement re-traiter l’arête incidente à a. En effet, lorsque a est l’extrémité d’un chemin d’arêtes pendantes, sa suppression fait que l’arête précédente du chemin devient pendante et doit être supprimée (alors qu’avant la suppression de a, cette arête n’était pas pendante et devait être conservée). Ce traitement doit être itéré tant que l’arête courante est supprimée.
Lors de la seconde étape de l’algorithme, nous supprimons les sommets pour obtenir la représentation minimale composée d’un seul sommet. Chaque sommet de degré deux est supprimé. Pour les autres sommets s (de degré supérieur à deux), nous devons tester s’il existe une arête a non-boucle incidente à s. Si c’est le cas, le sommet peut-être supprimé après avoir décalé les arêtes différentes de a sur un autre sommet. Sinon, c’est que nous avons obtenu la représentation minimale de la surface avec un seul sommet incident uniquement à des boucles, et le sommet ne doit pas être supprimé.
Nous pouvons voir Figs. 6.28 et 6.29 deux exemples de cartes minimales : le premier exemple est obtenu à partir d’une 2G-carte représentant un tore à deux trous, et le second à partir d’une 2G-carte représentant une bouteille de Klein. Nous montrons dans ces deux exemples la 2G-carte initiale, celle obtenue à la fin de la première étape de suppression des arêtes, puis la 2G-carte finale qui est la représentation minimale. Dans le premier cas, cette G-carte est composée d’une face, quatre arêtes et d’un sommet : la caractéristique d’Euler-Poincaré est égale à moins deux. Dans le second cas, la G-carte est composée d’une face, de deux arêtes, et d’un sommet : la caractéristique d’Euler-Poincaré est égale à zéro.
[a][b]
[c]
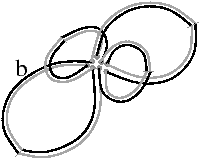
Figure 6.28: Un exemple de G-carte minimale d’un tore à deux trous. (a) La 2G-carte initiale. (b) La G-carte obtenue après les suppressions d’arêtes. (c) La G-carte obtenue après les suppressions de sommets. Les brins en noirs appartiennent à l’orbite ⟨α0∘α1⟩(b).
[a][b]
[c]
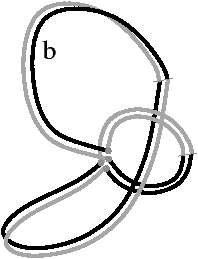
Figure 6.29: Un exemple de G-carte minimale de la bouteille de Klein. (a) La 2G-carte initiale. (b) La G-carte obtenue après les suppressions d’arêtes. (c) La G-carte obtenue après les suppressions de sommets. Les brins en noirs appartiennent à l’orbite ⟨α0∘α1⟩(b).
Pour tester le degré d’une arête, nous utilisons à nouveau des arbres union-find [Tar75] (de manière similaire au calcul du niveau 2 présenté Section 4.4.2 page ??). Nous initialisons ces arbres avant de commencer les simplifications en associant un arbre différent à chaque face de la G-carte. Lors de la suppression d’une arête incidente à deux faces distinctes, nous fusionnons les deux arbres associés (face(d) et face(β2(d))). De ce fait, tester si une arête est de degré un (c-à-d incidente deux fois à la même face) se fait simplement en testant si find(d)=find(β2(d)), et la complexité amortie de ce test peut-être considéré en temps constant.
Pour montrer la validité de notre algorithme, nous avons prouvé que l’homologie est préservée par les opérations utilisées, et que la G-carte obtenue est minimale (cf. [DPF06]). Pour montrer que l’homologie est préservée, nous avons fait un parallèle entre l’opération de suppression d’arête et l’opération de réduction utilisée dans [KMS98], pour laquelle les auteurs ont prouvé que l’homologie était préservée. La preuve que la G-carte est minimale s’effectue par contradiction en supposant qu’elle est composée de plus d’un sommet, ce qui contredit le fait que toute les arêtes non boucles ont été supprimées.
De plus, les arêtes de la G-carte résultante de notre algorithme sont les générateurs du premier groupe d’homologie (sauf dans le cas particulier de la sphère où la 2G-carte minimale est composée d’une face, d’une arête et de deux sommets alors qu’il n’y a pas de générateur du premier groupe d’homologie). En effet, ces arêtes sont des cycles car ce sont toutes des boucles et donc leur bord est nul. De plus, nous pouvons distinguer les générateurs libres des générateurs de torsions. Pour cela, nous orientons la face de la G-carte obtenue, en marquant les brins de l’orbite <α0 ∘ α1>(b) où b est un brin quelconque de la G-carte. Pour chaque arête de la G-carte désignée par un de ses brins b, si b et α2(b) sont tous les deux marqués, le générateur associé à cette arête est de torsion, sinon il est libre. Dans l’exemple de la Fig. 6.5.1, nous pouvons vérifier que les deux générateurs sont libres car il n’existe pas de brin b marqué avec α2(b) également marqué. Par contre dans l’exemple de la Fig. 6.5.1, nous pouvons observer qu’un générateur est libre et que l’autre est de torsion.
Nous avons étendu l’algorithme précédent pour calculer les générateurs des groupes d’homologie d’un objet 3D orientable, c’est à dire un objet 3D bordé d’une ou plusieurs surfaces orientables.
Nous nous sommes pour cela inspiré du travail présenté dans [DG98] qui étudie l’homologie des variétés 3D. Ils montrent deux résultats que nous utilisons par la suite : (1) Pour un objet X bordé par j+1 surfaces s0,...,sj, où s0 est la surface externe de X, alors l’ensemble {s1,...,sj} est une base du deuxième groupe d’homologie H2(X) ; (2) les générateurs longitudinaux de s0 plus les générateurs latitudinaux de {s1,...,sj} forment une base du premier groupe d’homologie H1(X). Intuitivement, pour une surface bordant un objet, un générateur est longitudinal s’il «entoure» un tunnel de l’objet (donc «du vide» pour l’objet), et il est latitudinal sinon (et dans ce cas il «entoure» de «la matière» de l’objet) (cf. [DG98] pour les définitions précises).
Sur l’exemple de la Fig. 6.5.2, la surface externe s0 borde un tore à trois tunnels. Cette surface à donc six générateurs : trois longitudinaux, chacun entourant un tunnel du tore, et trois latitudinaux reliant ces trois premiers générateurs (non représentés). La surface bordant la cavité torique est composée de deux générateurs : un longitudinal entourant le tunnel du tore (non représenté) et un latitudinal entourant le tunnel du complémentaire du tore. L’ensemble des générateurs du premier groupe d’homologie est composé des trois générateurs longitudinaux de la surface externe plus le générateur latitudinal de la cavité torique. Il faut noter que le premier groupe d’homologie de la sphère est trivial, donc il n’y a pas de générateur dans ce cas.
[a][b]
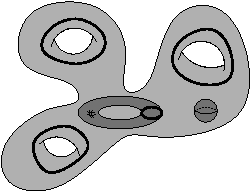
Figure 6.30: (a) Un objet 3D ayant trois tunnels et deux cavités. (b) Le générateur latitudinal de la cavité torique, et les trois générateurs longitudinaux de la surface externe de l’objet forment une base du premier groupe d’homologie de l’objet.
Le principe de l’Algorithme 6.31 consiste, comme l’algorithme précédent dans le cas 2D, à simplifier la 3G-carte en utilisant les opérations de suppression tout en préservant l’homologie de la 3G-carte.
- Entrées : Une 3G-carte G décrivant une subdivision orientable, avec chaque cellule homéomorphe à une boule topologique
- Résultat : La subdivision minimale homologue à G
1.
Pour chaque face f de G faire
Si le degré de f est 2 alors
Supprimer f;
Sinon Si f est une face pendante alors
empiler(P,f);
Faire
f ← dépiler(P);
empiler dans P toute les faces pendantes incidentes à f;
Supprimer f;
Tant que non vide(P);
Sinon Marquer f comme face fictive;
2. Supprimer toutes les faces fictives;
3. Marquer la surface externe;
4. Calculer les générateurs H1 de chaque surface;
5.
Si la surface externe est une sphère alors
ext ← la seule arête de la surface externe;
Sinon Pour une arête sur deux e de la surface externe faire
Insérer une face fictive incidente à e;
ext ← e;
Pour chaque surface interne s faire
Si s est une sphère alors
int ← la seule arête de s;
Sinon Pour une arête sur deux e de s faire
Insérer une face fictive incidente à e;
int ← e;
Insérer une face fictive face entre int et ext;
Figure 6.31: Algorithme : Simplification d’une subdivision 3D dans sa forme minimale.
Nous simplifions progressivement la subdivision d’un objet 3D dans lequel chaque cellule est initialement homéomorphe à une boule, en utilisant les opérations de suppression par dimension décroissante. Tout d’abord nous supprimons des faces tout en conservant les volumes homéomorphes à des boules. Pour cela, nous gardons des faces fictives (qui sont l’extension des arêtes fictives). Ces faces sont de degré un (c-à-d incidentes deux fois au même volume) et non pendantes. À la fin de cette étape nous obtenons une 3G-carte composée d’un seul volume. Ensuite, nous pouvons nous ramener au cas 2D présenté section précédente, mais nous devons pour cela supprimer les faces fictives. En effet, après cette suppression nous obtenons un ensemble de surfaces 2D et nous pouvons utiliser l’Algorithme 6.27 pour chacune d’elle, ce qui nous donne un ensemble de 2G-cartes minimales. Pour reconstruire la 3G-carte minimale correspondante à l’objet initial, nous insérons les faces fictives préalablement supprimées afin de rendre la 3G-carte connexe et le volume homéomorphe à une boule. Ces faces correspondent aux cellules implicites définies Section 6.3.1 pour le calcul des nombres de Betti.
Nous détaillons maintenant plus précisément chaque étape de l’algorithme de simplification. La première étape (ligne 1) consiste à supprimer toutes les faces de degré deux et toutes les faces pendantes jusqu’à obtenir un seul volume homéomorphe à une boule. Le principe est similaire à l’algorithme 2D, où lorsqu’une face pendante est supprimée, nous devons re-considérer les faces adjacentes pour traiter le cas où elles deviennent à leur tour pendantes. Durant cette étape, nous marquons les faces fictives (qui sont des faces de degré un non pendantes). À la fin de cette étape, nous obtenons une 3G-carte composée d’un seul volume homéomorphe à une boule, des faces réelles (composées de brins 3-libres) et des faces fictives (composées de brins non 3-libres).
La Fig. 6.5.2 montre un exemple de résultat obtenu à la fin de cette première étape. Nous pouvons vérifier sur cet exemple que les faces fictives sont de deux types différents : celles qui bouchent des tunnels, et celles qui relient entre elles différentes surfaces pour garder la carte connexe.
[a][b]
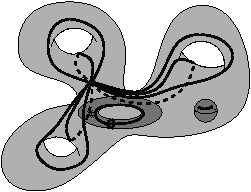
La deuxième étape de l’algorithme (à partir de la ligne 2) va travailler sur chaque surface de l’objet. Pour cela, nous supprimons chaque face fictive, ce qui va déconnecter les différentes surfaces qui pourront être considérées séparément, et marquons la surface externe. La distinction entre la surface externe et les autres surfaces est nécessaire pour calculer les générateurs H1, car pour la surface externe nous devons considérer les générateurs longitudinaux tandis que pour les autres surfaces nous devons considérer les générateurs latitudinaux. Pour marquer la surface externe, nous devons trouver un brin de départ (par exemple le brin associé à la plus petite coordonnées géométrique), puis parcourir la surface en utilisant l’orbite ⟨α0,α1,α2⟩ à partir de ce brin.
L’étape d’après (ligne 4) consiste à calculer les générateurs H1 de chaque surface de manière indépendante. Nous utilisons pour cela l’algorithme 2D présenté section précédente. En effet, même si nous travaillons sur une 3G-carte, tous ses brins sont 3-libres ce qui nous permet de considérer chaque composante connexe comme une 2G-carte.
À la fin de cette étape, nous avons obtenu la représentation minimale de chaque surface. Cette représentation est composée d’une face, une arête et deux sommets pour une sphère, et d’une face, 2k arêtes et un sommet pour un tore à k trous. Nous devons maintenant reconstruire la subdivision minimale de l’objet 3D. C’est l’objet de la dernière étape de l’algorithme (à partir de la ligne 5) qui va ajouter des faces fictives pour reconstruire une 3G-carte connexe, et composée d’un seul volume homéomorphe à une boule.
Pour cela, nous insérons une face fictive entre ext, un brin de la surface externe, et un brin de chaque surface interne, ce qui rend la 3G-carte connexe (nous ne différencions pas ici les générateurs latitudinaux et les longitudinaux car topologiquement ils ont le même rôle et donc cette distinction n’intervient pas pour le calcul des groupes d’homologies. Nous reviendrons par contre sur cette distinction qui intervient pour plonger les générateurs). Nous insérons également une face fictive pour boucher chaque tunnel. Cela se fait en insérant une face pour un brin sur deux de chaque surface. En effet, chaque arête d’un tore à k trous est une boucle, et il y a 2k arêtes. En insérant k faces fictives le long de ces boucles, nous bouchons bien chaque tunnel et obtenons un volume homéomorphe à une boule (cf. Fig. 6.5.2).
[a][b]
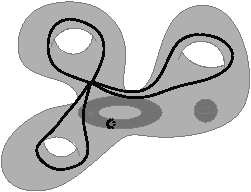
Figure 6.33: (a) La G-carte minimale obtenue à la fin de l’algorithme (représentation partielle, les faces fictives liant la surface externe et les surfaces internes ne sont pas représentées). Cette carte est homologue à la subdivision initiale. (b) Les générateurs H1 sont composés de toutes les arêtes non-incidentes à une face fictive, et non-incidentes à une sphère.
À la fin de l’algorithme, nous obtenons une carte où chaque cellule est homéomorphe à une boule. Cette propriété est nécessaire afin de prouver que la G-carte est homologue à l’objet initial. De plus, cette carte est composée de j+1 faces réelles, une pour chaque surface de la subdivision initiale, et elle contient directement les générateurs des groupes d’homologie :
Comme en 2D, la 3G-carte obtenue est homologue à l’objet initial, et permet de calculer directement les générateurs des groupes d’homologie de l’objet initial par une simple caractérisation des cellules. De plus, ce principe de simplification par dimension décroissante est intéressant dans le but d’étendre cette méthode en dimension quelconque.
Nous prouvons la validité de notre méthode en montrant que l’homologie de l’objet est préservée durant les simplifications, et que les générateurs de l’homologie peuvent être directement obtenus. Ces preuves reposent principalement sur les travaux de [KMS98] et de [DG98] (cf. [DPF08] pour ces preuves). Pour cela, nous faisons le lien entre l’opération de réduction dans les complexes simpliciaux et notre opération de suppression de face, et utilisons les travaux de [KMS98] qui montrent que ajouter une face le long de chaque générateur latitudinal coupe le volume correspondant en un objet homéomorphe à une boule. Pour la caractérisation directe des générateurs, nous utilisons les deux propriétés énoncées en début de ce chapitre et provenant de [DG98]. Pour H2(X), nous récupérons l’ensemble des surfaces internes, et pour H1(X) les générateurs longitudinaux de la surface externe, et les générateurs latitudinaux des surfaces internes. Pour distinguer les deux types de générateurs, nous utilisons les faces fictives. En effet, les arêtes incidentes aux faces fictives n’appartient pas aux générateurs de H1(X) par construction. De ce fait, nous obtenons une caractérisation simple des arêtes appartenant aux générateurs du groupe d’homologie H1(X) qui est combinatoire, et qui est plus simple que la méthode utilisée dans [DG98] et consistant à utiliser le nombre de liaisons et à perturber les générateurs.
L’Algorithme 6.31 permet de calculer la 3G-carte minimale homologue à la subdivision initiale, ce qui nous permet de calculer directement les générateurs des groupes d’homologie de l’objet. Mais il n’est pas directement possible de retrouver le lien entre ces générateurs et les cellules de la subdivision initiale pour H1.
C’est par contre possible pour H2, car chaque face réelle de la carte minimale va fournir un brin de départ pour une surface de la subdivision originale. Parcourir cette surface se fera ensuite simplement par un parcours de surface en sautant les brins non 3-libres, qui appartiennent forcément aux faces fictives
Pour les générateurs de H1, la difficulté concerne la dernière étape de l’algorithme qui insère des faces fictives en prenant une arête sur deux des surfaces, sans propriétés particulières sur ces arêtes. Cela suffit pour le calcul des groupes d’homologie car ces arêtes jouent topologiquement des rôles identiques, mais cela pose problème pour le lien avec la subdivision initiale car les plongements de ces arêtes n’ont plus des rôles équivalents (il faut conserver les arêtes entourant uniquement du vide par rapport à l’objet). Pour résoudre ce problème, il suffit d’ajouter un test supplémentaire dans l’Algorithme 6.31 :
Avec ces deux modifications, les générateurs H1 peuvent maintenant être plongés sur la G-carte initiale. Mais pour cela, il faut conserver lors des opérations de suppression d’arêtes et de décalage d’arête un lien entre les arêtes modifiées et les arêtes de la subdivision initiale, de manière similaire à ce que nous avons présenté au chapitre 5 pour les chemins de connexion.
Dans ce chapitre, nous avons présenté plusieurs méthodes permettant de calculer différents invariants topologiques pour les cartes : un algorithme de calcul de la caractéristique d’Euler-Poincaré, le calcul des nombres de Betti, avec une version de mise à jour locale lors des opérations de suppression, le schéma polygonal canonique d’une surface, et les groupes d’homologie d’une surface fermée, et d’un volume orientable fermé.
Ces différentes méthodes ont toutes comme point commun d’être en lien avec les opérations de suppression et contraction, qui sont utilisées dans des cadres différents, mais toujours en contrôlant l’évolution des caractéristiques topologiques. Ce sont ces opérations de simplification qui nous ont permis de proposer des algorithmes efficaces permettant de mettre à jour les invariants topologiques de manière locale lors de ces opérations.
Par contre nos travaux ne sont pas tous au même niveau concernant les différents invariants topologiques. En effet, notre objectif global est de fournir des outils génériques autour des cartes, et nous avons pour le moment restreint le calcul des nombres de Betti et des générateurs des groupes d’homologie à une sous-classe d’objets (2D ou 3D orientable fermé).
Cela ouvre donc directement des perspectives à ce chapitre qui sont l’extension des méthodes proposées en dimension quelconque et à des objets quelconques (ouverts ou non, orientables ou non). Pour cela, nous devons étudier plus précisément la notion de face fictive, et plus généralement en dimension n de cellule fictive, pour éviter l’étape de déconnexion utilisée dans l’algorithme de calcul des générateurs de l’homologie 3D. En effet, en utilisant un procédé similaire à celui du décalage des arêtes en 2D, nous devrions pouvoir éviter cette étape en décalant les faces fictives. Cela aurait l’avantage de ne pas avoir perdu une information durant la déconnexion (la différence entre les générateurs longitudinaux et latitudinaux), et cela permettrait également plus facilement de faire le lien entre la carte minimale et la représentation initiale de la subdivision.
Pour proposer une méthode générale de calcul des groupes d’homologie en nD, nous avons défini dans [APDL09] un opérateur de bord en dimension quelconque, qui est l’étape préalable à la définition directe de l’homologie cellulaire. De plus, nos travaux actuels ont principalement porté sur l’utilisation des opérations de suppression, et il serait également intéressant d’étudier le lien avec l’opération de contraction. Une autre piste que nous avons pour le moment étudiée en 2D dans [PIH+07, PIK+09] est l’utilisation d’une pyramide de cartes pour guider les calculs des groupes d’homologie. L’idée consiste à construire une pyramide, en préservant l’homologie des objets manipulés, puis de manière un peu similaire aux algorithmes de mise à jour locaux, à calculer les générateurs de l’homologie sur le niveau au sommet de la pyramide, puis à propager ces générateurs de niveau en niveau jusqu’à la base. Ce type de technique a l’avantage d’effectuer le calcul initial sur un niveau contenant très peu de cellules (proche d’une carte minimale), mais également de simplifier la propagation en la découpant en plusieurs petites étapes. Un autre avantage de ce type de technique est qu’il est possible de déformer la géométrie des générateurs lors de leurs projection de niveau en niveau, en garantissant bien évidemment la préservation de leur topologie.
Nous allons maintenant nous intéresser aux applications des modèles et des opérations que nous avons présentés tout au long de ce mémoire. Nous avons principalement deux champs applicatifs privilégiés qui sont la modélisation géométrique et le traitement d’images. Dans les deux cas, nos préoccupations centrales tournent autour de la topologie et de son apport dans les différentes opérations.
Dans ce chapitre, nous présentons quelques utilisations que nous avons pu faire des modèles et opérations présentés tout au long de ce mémoire. Cela nous permet d’illustrer une nouvelle fois l’intérêt de la généricité de nos travaux qui peuvent s’appliquer à différentes dimensions et dans différents domaines, bien que principalement en modélisation géométrique et traitement d’images 2D et 3D. Nous présentons également la façon dont nous avons utilisé la méthode de mise à jour locale des nombres de Betti afin de guider un algorithme de segmentation d’images 3D en intégrant un critère topologique. Ce travail est un premier résultat démontrant un apport important de l’utilisation de modèles combinatoires de haut niveau. Nous verrons que cela ouvre de nombreuses perspectives prometteuses sur la poursuite de ces travaux.
Le plan de ce chapitre est le suivant. Nous commençons Section 7.1 par présenter le modeleur géométrique à base topologique Moka qui est défini à partir d’un noyau de cartes généralisées 3D. Ce modeleur est à la base de nombreux travaux, dont un modeleur de bâtiments. Il est également l’outil d’expérimentation avec lequel il est facile de tester de nouvelles méthodes. Nous avons par exemple implanté dans Moka certaines méthodes de calcul d’invariants topologiques présentés au chapitre 6. Nous présentons ensuite Section 7.2 l’utilisation des cartes topologiques 2D et 3D (qui sont définies à partir de noyaux de cartes combinatoires pour des raisons d’espace mémoire) pour la mise en œuvre d’algorithmes de segmentation d’images. La Section 7.3 propose l’extension de ces méthodes pour la segmentation multi-échelle en utilisant les pyramides de cartes. Enfin, nous concluons et donnons des perspectives de ce chapitre à la Section 7.4.
Moka1 est un modeleur géométrique 3D à base topologique, disponible en téléchargement libre sur http://moka-modeller.sourceforge.net/. Ce projet a débuté en 1999 durant un stage de Master que j’ai encadré, puis a été poursuivi dans le cadre du projet RNTL Nogemo de Septembre 2001 à Août 2004. Le principal développeur a été Frédéric Vidil, ingénieur embauché dans le cadre de ce projet, et j’ai été le second développeur principal en collaboration avec Frédéric. Depuis la fin du projet Nogemo, je suis le chef de projet et le principal développeur de Moka.
Figure 7.1: Capture d’écran de Moka avec une scène comportant différents objets : un tore obtenu par création d’objet de base, une bouteille de Klein obtenue par extrusion, couture puis lissage, et un avion obtenu par importation d’un fichier au format off.
Ce modeleur se base sur un noyau de 3G-cartes qui fournit les opérations de manipulations de base des objets 3D. Plusieurs surcouches ont été développées afin d’enrichir ce noyau de nombreuses fonctionnalités. Moka contient actuellement plus de 20 types d’opérations différentes, qui se déclinent pour la plupart en plusieurs variantes selon la dimension ou selon plusieurs options (cf. Figs. 7.2 et 7.3 pour quelques exemples d’opérations). Ces opérations principales peuvent être regroupées en grandes catégories :
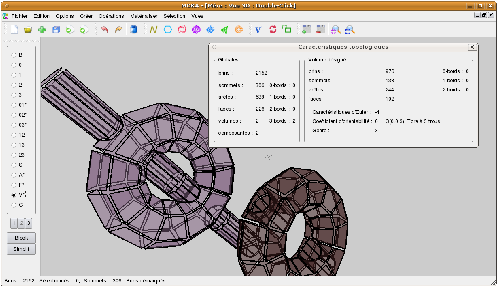
Figure 7.3: Exemple d’opération booléenne entre un tore et un cylindre. Nous avons ici conservé l’union des deux objets, et le résultat du tore moins le cylindre. La boîte de dialogue montre le calcul du nombre de cellules et de la caractéristique d’Euler-Poincaré de ce résultat qui est un tore à trois trous.
De par sa richesse en fonctionnalités et sa stabilité, Moka est un outil d’expérimentation très riche dans lequel il est facile d’intégrer et tester de nouvelles méthodes issues de problématiques de recherche. Nous avons par exemple intégré dans Moka la plupart des méthodes de calcul d’invariants topologiques présentées au chapitre 6. Nous avons pu ainsi tester nos algorithmes de simplification en forme minimale, en utilisant les invariants topologiques pour vérifier que la topologie des objets est préservée durant les simplifications.
Enfin, de par sa généricité et son nombre important de fonctionnalités, Moka a servi de base de développement à plusieurs projets de modélisation géométrique. La plupart du temps, ces projets ont des contraintes spécifiques, qu’il suffit de rajouter dans une surcouche spécifique, mais les opérations de base restent valides et utilisables. Les principaux projets ayant utilisé Moka sont VORTISS, un projet labélisé à l’ANR MDCA, dont l’objectif est la reconstruction d’organes pour l’interaction temps réel en simulation chirurgicale ; un projet de générateur d’évolutions géologiques par animation basée sur la topologie [LSM08, LSM09] ; un projet de nomination persistante afin de faire du suivi d’objets et de la réévaluation de modèles [BMSB07] ; un projet de modélisation géométrique du sous-sol [BSP+04] ; un modeleur hiérarchique de complexes architecturaux [Fra04, FML06].
Parmi ces projets, j’ai participé à l’encadrement de la thèse de Sébastien Horna [Hor08] dont l’objectif était de proposer une méthode de reconstruction topologique de complexes architecturaux 3D à partir de plans numériques 2D [HDMB07, HMDB09]. Nous avons pour cela mis en œuvre un outil de reconstruction de bâtiments 3D en utilisant les informations contenues dans les plans d’architecte, et en contrôlant la validité du résultat obtenu grâce à des contraintes métier. Nous avons proposé des opérations automatiques, mais aussi certaines opérations semi-automatiques permettant d’aider et de guider la reconstruction d’un bâtiment complet en un nombre réduit d’interactions.
La reconstruction est réalisée en plusieurs étapes, chacune utilisant des opérations de base de Moka et des propriétés des G-cartes afin de contrôler la validité de la subdivision obtenue. Durant ce processus, les opérations géométriques sont toutes réalisées en Epsilon geometry [SSG89] (test d’intersection, de colinéarité, trouver les mêmes sommets…). Avant de débuter le processus de reconstruction, les plans d’origine doivent tout d’abord être importés dans Moka. Ces plans sont au format DXF (Drawing eXchange Format) qui est un format très répandu en CAO (cf. Fig. 7.4 pour quelques exemples). Les données récupérées sont un ensemble de segments qui représentent les plans, et nous construisons alors une G-carte dans Moka qui contient une arête pour chaque segment.
[a][b]
[c][d]
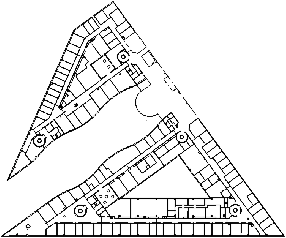
Figure 7.4: Exemple de plans 2D traités : (a) Étage 3 Sp2mi, 8120 brins ; (b) LEA, 17168 brins ; (c) LR, 25976 brins ; (d) Étage 0 Sp2mi, 33508 brins.
Nous avons à ce stade un ensemble une G-carte composée d’arêtes déconnectées. Le processus de reconstruction d’un modèle valide 2D est découpé en 5 étapes :
La première étape consiste à corriger les problèmes géométriques de l’ensemble des segments. En effet, l’objectif initial des architectes lors de la création des plans est d’avoir un résultat visuel satisfaisant. Peu importe alors que deux arêtes soient superposées, ou que deux arêtes se croisent en dehors de leurs extrémités. Mais ces cas posent problème dans notre approche car ils empèchent de garantir que nous reconstruisons bien une partition de l’espace. Afin de résoudre ces problèmes, chaque couple d’arêtes supperposées est traité et corrigé de la manière détaillée Fig. 7.5. Comme la complexité de ce processus est quadratique en le nombre total d’arêtes, nous avons utilisé une grille régulière afin d’accélérer les temps de calcul en limitant la recherche à un petit nombre d’arêtes.
[a][b]

Figure 7.5: Résolution des problèmes d’arêtes supperposées. (a) Lorsqu’une arête est incluse dans une autre, elle est supprimée. (b) Lorsqu’une arête a une partie en commun avec une autre, elle est réduite afin de supprimer cette partie. Le choix de l’arête à réduire n’importe pas dans le résultat final. En effet, le sommet de l’arête qui a été déplacé (A′ sur cet exemple) sera inséré à nouveau, lorsque c’est nécessaire, par la phase traitant les problèmes d’intersection d’arêtes.
Le traitement des problèmes d’intersection d’arêtes est réalisé en testant si l’intersection entre chaque couple d’arêtes est vide ou est une extrémité des deux arêtes. Lorsque ce n’est pas le cas, les deux arêtes s’intersectent en dehors de leurs extrémités. Le problème est alors résolu en insérant un sommet sur l’une ou sur les deux arêtes selon les configurations qui sont détaillées Fig. 7.6. Comme pour le traitement des arêtes confondues, nous utilisons également une grille régulière afin d’accélérer la recherche sur les couples d’arêtes ayant une intersection non vide.
[a][b]
[c]
[d]
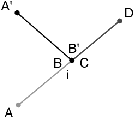
Figure 7.6: Résolution des problèmes d’intersection d’arêtes. (a) Lorsque deux arêtes s’intersectent en leurs milieux, (b) il faut insérer un sommet au point d’intersection sur les deux arêtes. (c) Lorsque deux arêtes s’intersectent en l’extrémité de l’une mais pas de l’autre, (d) il faut insérer un sommet seulement sur une arête.
Nous avons maintenant un ensemble d’arêtes disjointes sans problème géométrique. Nous passons alors à la seconde phase qui consiste à relier ces arêtes entres elles afin de former des faces. Nous utilisons pour cela un algorithme d’interclassement qui consiste à trier angulairement les arêtes incidentes à un même sommet, puis à les relier deux à deux par α1 en cousant à chaque étape l’arête courante avec la prochaine arête dans l’ordre angulaire. Après avoir traité toutes les arêtes du sommet, il reste à fermer la boucle en cousant la dernière arête avec la première. Ce processus est illustré Fig. 7.7. Après avoir traité toutes les arêtes de la G-carte, nous avons défini les liaisons α1 de chaque brin, ce qui fait que la G-carte est désormais 1-fermée. Comme elle était 0- et 2-fermée par construction (chaque arête est créée avec quatre brins et ses liaisons α0 et α2), la 2G-carte est donc fermée. Durant ce processus, nous devons trouver toutes les arêtes qui partagent une même extrémité, et à nouveau l’utilisation d’une grille régulière permet d’accélérer cette recherche en la limitant aux brins appartenant à la même cellule de la grille. Il faut noter que ce travail pourrait sans doute être amélioré en utilisant un algorithme de calcul d’arrangements de segments [EGS90], ainsi qu’en utilisant des calculs géométriques exacts [Yap04].
[a][b]
[c]
[d]
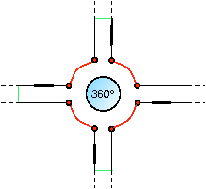
Figure 7.7: Illustration du processus d’interclassement. (a) Configuration initiale dans laquelle nous avons un ensemble d’arêtes partageant une même extrémité. (b) Première liaison par α1. (c) Résultat après avoir traité toutes les arêtes. (d) Résultat final après avoir fermé la boucle en cousant la dernière arête avec la première.
L’étape suivante consiste à corriger le problème survenant lorsque la G-carte est composée de plusieurs composantes connexes. En effet, comme expliqué au chapitre 4 dans le cadre des cartes topologiques, ces différentes composantes sont déconnectées et sans lien entre elles. De ce fait, les faces de la subdvision ne sont pas correctement représentées dans la carte. La solution utilisée ici est à nouveau l’ajout d’arêtes fictives rendant la carte connexe, et liant entre elles les différentes composantes connexes (cf. Fig. 7.8). Pour chaque composante connexe C, une recherche est effectuée afin de trouver la face contenant géométriquement C. Une arête fictive est alors insérée entre la face externe de la composante connexe et sa face englobante. Les sommets support de cette arête sont choisi de telle manière d’éviter que l’arête insérée intersecte une autre arête (cf. [Hor08] pour plus de détails).
[a][b]
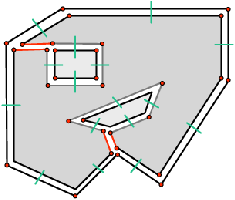
Figure 7.8: Ajout d’arêtes fictives pour rendre la carte connexe. (a) Configuration initiale composée de trois composantes connexes. (b) Carte finale après avoir inséré deux arêtes fictives.
Le dernier problème pouvant se poser est la présence d’arêtes pendantes. Ce problème est lié à l’application car ce type d’arête correspond ici à une incohérence qui est due à une imprécision numérique ou à l’omission d’un objet par l’architecte (cf. quelques exemples Fig. 7.9).
[a][b]
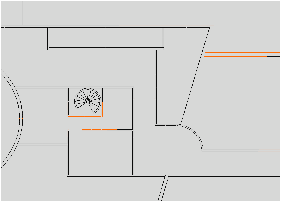
Figure 7.9: Exemple d’arêtes pendantes (en rouge) détectées dans un plan 2D. (a) Des erreurs numériques font que les arêtes associées aux marches de l’escalier ne touchent pas le rectangle englobant. (b) Un exemple d’objet manquant, ici probablement une porte.
La correction de ce problème dépend du contexte de l’arête pendante et ne peut pas être réalisée de manière totalement automatique. En effet, selon les cas, cette correction va consister à :
Ces quatre opérations sont proposées à l’utilisateur, avec des variantes permettant par exemple d’appliquer simultanément un ensemble d’opérations, ou d’essayer automatiquement de prolonger chaque arête pendante en dessous d’un seuil donné afin de corriger automatiquement les arêtes très proches qui sont souvent issues d’erreurs de précision numérique.
Nous avons désormais une partition 2D valide. La dernière étape consiste à associer une sémantique à chaque face qui sera utilisée ensuite lors de l’extrusion du plan afin de construire le modèle 3D. Nous avons défini des étiquettes sémantiques (mur, façade, sol, plafond, porte, fenêtre, escalier, pièce), chaque face de la carte étant associée avec exactement une étiquette. Nous avons ensuite défini des contraintes de voisinage (par exemple une porte doit être adjacente à deux murs et deux pièces) et nous utilisons ces contraintes afin de déterminer automatiquement le plus d’étiquettes sémantiques possible. Nous commençons par affecter la façade car nous savons que c’est la face externe de la 2G-carte, qui se retrouve simplement en utilisant les coordonnées des sommets.
Ensuite, nous avons défini un algorithme de propagation des sémantiques qui utilise les contraintes de voisinages pour propager les valeurs sémantiques de proche en proche. Enfin, nous avons proposé des heuristiques permettant de déterminer automatiquement les étiquettes sémantiques non affectées en utilisant des caractéristiques géométriques des faces (par exemple des coefficients d’élongation, le co-degré des faces…). Nous avons offert la possibilité à l’utilisateur de vérifier et corriger la sémantique associée à chaque élément du modèle, tout en contrôlant à chaque fois que les contraintes de voisinages soient respectées.
[a][b]
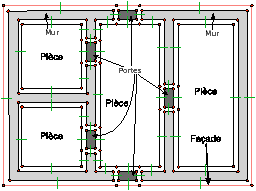
Figure 7.10: Résultat obtenu à la fin des 5 étapes de reconstruction du modèle 2D. (a) Le plan initial. (b) La 2G-carte reconstruite avec sa sémantique associée.
À la fin des cinq étapes de reconstruction 2D, nous obtenons une 2G-carte valide correspondant au plan initial, avec une sémantique associée à chacune de ses faces (cf. Fig. 7.10). Nous avons désormais toutes les informations nécessaires afin de transformer ce modèle en bâtiment 3D. Cette reconstruction 3D se décompose à son tour en trois étapes :
La première étape est l’extrusion du modèle 2D qui permet de le convertir en modèle 3D. Comme nous pouvons voir Fig. 7.11, il existe trois types d’extrusion selon la sémantique de la face. L’opération d’extrusion existe déjà dans Moka, la seule difficulté est ici de l’appeler avec les bons paramètres, puis ensuite de relier les différents volumes issus des trois types d’extrusion. Après cette étape, nous obtenons un modèle 3D où chaque face du plan 2D est devenue un volume 3D. Durant cette étape d’extrusion, nous propageons correctement la sémantique des faces aux volumes créés.
[a][b]
[c]
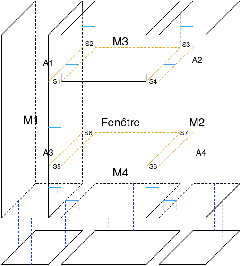
Figure 7.11: Les trois types d’extrusion possibles en fonction de la sémantique des faces. (a) Cas général (pièce, mur, façade) : extrusion le long d’un chemin composé d’une seule arête. (b) Cas d’une porte : extrusion le long d’un chemin composé de deux arêtes. La première arête pour la porte elle-même, la seconde pour le pan de mur au dessus de la porte. (c) Cas d’une fenêtre : extrusion le long d’un chemin composé de trois arêtes. La première arête pour le mur en dessous de la fenêtre, la seconde pour la fenêtre elle-même, et la troisième pour le mur au dessus de la fenêtre.
La seconde étape consiste à créer un volume sol et un volume plafond en dessous (resp. en dessus) du résultat de l’extrusion. Ces volumes sont construits à partir d’une copie des faces inférieures (resp. supérieures) de l’étage, comme illustré Fig. 7.1. Ces volumes ont deux raisons d’être : la première raison est physique, car ils correspondent à la réalité d’un bâtiment et peuvent avoir un impact, par exemple sur des simulations de propagation d’ondes. La seconde raison est qu’ils servent lors de la superposition de plusieurs étages. En effet, comme illustré Fig. 7.12, lorsque les deux étages ont la même géométrie, cette superposition revient à supprimer la face supérieure du plafond du premier étage, et la face inférieure du sol de l’étage à superposer, puis à relier entre elles les faces qui étaient incidentes à ces faces supprimées.
Figure 7.12: Sol, plafond et superposition d’étages. (a) Illustration des volumes sol et plafond. (b) Configuration initiale avant la superposition. (b) La face supérieure du plafond et la face inférieure du sol sont supprimées. (c) Les faces adjacentes sont reliées entre elles.
Lorsque les étages ont des géométries différentes, une étape supplémentaire est nécessaire afin de découper la géométrie de la face entre les deux étages, de manière à créer une sous-partie identique. Cette découpe s’effectue au moyen des opérations d’insertion de sommet et d’arête. C’est ensuite le long de cette partie commune que les étages sont superposés en se ramenant au cas précédent où les deux étages avaient la même géométrie (cf. Fig. 7.13 pour deux exemples d’étages superposés).
[a][b]
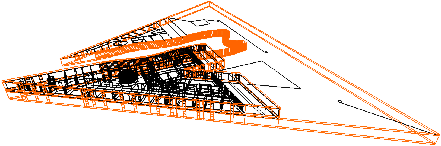
Figure 7.13: Deux exemples de résultats obtenus après extrusion et superposition de deux étages. (a) Cas de deux étages ayant la même géométrie. (b) Cas de deux étages ayant des géométries différentes.
La dernière étape du processus de reconstruction 3D consiste à relier les étages entre eux en insérant des escaliers. Ces escaliers sont présents dans les plans 2D, et détectés automatiquement durant la phase d’assignation de sémantique par la présence de nombreuses petites faces similaires, en tenant compte des différents types d’escaliers possibles (droits, colimaçons…). Les faces étiquetées escalier ne sont pas extrudées durant l’étape précédente, et les escaliers sont construits par un algorithme spécifique. Afin de relier les étages entre eux, l’étage supérieur est découpé par un volume obtenu par extrusion de la forme de l’escalier dans le plan 2D, en utilisant les opérations booléennes de Moka (et plus précisément la soustraction, cf. Fig. 7.14 pour deux illustrations).
[a][b]

Figure 7.14: Visualisation du résultat d’insertion d’un escalier en colimaçon entre deux étages.
Nous avons également proposé d’autres opérations (non détaillées ici) permettant de finaliser le modèle 3D, comme la construction de toit qui est basée sur l’opération de chanfreinage, ou d’autres opérations de modification permettant à l’utilisateur de modifier soit le plan 2D reconstruit, soit directement le modèle 3D à la fin de l’ensemble de la reconstruction. Nous pouvons par exemple citer les fusions et découpes de pièces qui s’appuient sur les opérations de suppression et d’insertion, les translations de murs avec contraintes, la simplification et à l’inverse la triangulation des scènes, ou encore l’ameublement automatique (cf. Fig. 7.15), ou une visualisation interactive. Pour toutes ces opérations, nous utilisons à chaque fois différentes cellules de la subdivision, ainsi que les relations d’adjacence et d’incidence entre ces cellules, ce qui montre l’intérêt d’utiliser un modèle combinatoire décrivant toutes ces informations.
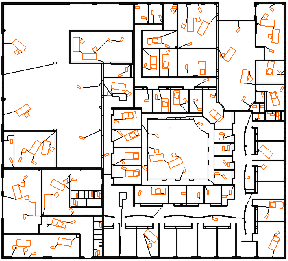
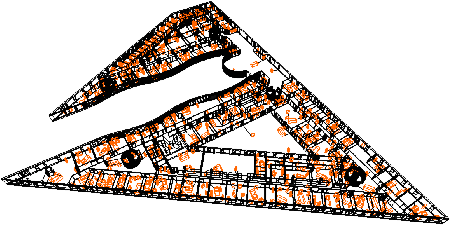
Figure 7.15: Exemple de résultat obtenu après l’opération d’ameublement automatique. (a) Pour le bâtiment LEA. (b) Pour le bâtiment Étage 0 Sp2mi.
Grâce à toutes ces opérations, nous disposons d’une chaîne complète de traitement partant de la reconstruction de bâtiments à partir de données numériques 2D jusqu’à la visualisation de ces environnements en utilisant une méthode de lancer de rayons interactive. Le point fort de notre approche est que chaque étape composant la chaîne de reconstruction utilise des contraintes géométriques, topologiques et sémantiques de notre modèle, ce qui garantit l’obtention d’un modèle valide. Nous pouvons voir Fig. 7.16 quelques résultats de reconstruction obtenus.



Figure 7.16: Bâtiments 3D reconstruits à partir de plans numériques, et visualisés avec le logiciel Pov-ray.
Notre deuxième champ d’expérimentation privilégié est le traitement d’images, en suivant et étendant l’idée initiale qui était d’utiliser un graphe d’adjacence de régions pour la résolution de problématiques de traitement d’images. Nous avons utilisé le modèle des cartes topologiques et les opérations proposées au chapitre 4 afin de mettre en œuvre des algorithmes de segmentation d’images. Nous avons tout d’abord adapté l’algorithme proposé dans [FH98, FH04], qui est basé sur une segmentation par croissance de régions en utilisant un critère basé sur la notion de contraste d’une région définie sur un graphe.
De manière simplifiée, la méthode originale consiste à associer un sommet du graphe à chaque pixel de l’image, à mettre une arête entre chaque couple de pixels 4-voisins (la méthode initiale était proposée en 2D), et à associer un poids à chaque arête, qui est une mesure non négative de dissimilarité entre les éléments associés aux deux sommets extrémités de l’arête. Avec ce formalisme, une segmentation de l’image est induite par un sous-ensemble d’arêtes : chaque composante connexe dans le sous-graphe induit par cet ensemble d’arêtes correspond à une région de la segmentation. Dans la méthode originale, les auteurs utilisent deux prédicats pour mesurer la dissimilarité des régions : le contraste interne à une région Int(R) qui est le poids de l’arête de coût maximum dans l’arbre couvrant de poids minimum des arêtes de cette région ; et le contraste externe entre deux régions Ext(R1,R2) qui est le poids de l’arête de coût minimum entre R1 et R2.
Deux régions R1 et R2 sont considérées comme similaires si Ext(R1,R2)>MInt(R1,R2), avec MInt(R1,R2)=min(Int(R1)+τ(R1), Int(R2)+τ(R2)) qui est le plus petit contraste interne des régions R1 et R2 pondéré par une fonction τ qui permet de paramétrer l’algorithme.
Le rôle de τ est de mitiger l’estimation du contraste interne lorsque celui-ci n’est pas représentatif comme par exemple pour les petites régions. Les auteurs suggèrent d’utiliser une fonction τ(R) = k / |R| avec |R| le nombre de pixels de R, et k une constante qui définit l’échelle de segmentation : en augmentant k, le nombre de régions fusionnées va augmenter. N’importe quelle fonction à valeurs positives peut être utilisée pour τ.
Dans leur article, les auteurs établissent une notion de segmentation optimale (pour le critère donné) qui est une segmentation n’ayant pas deux régions voisines pouvant fusionner (segmentation appelée sur-segmentation), ni une région pour laquelle il existe un raffinement qui n’est pas une sur-segmentation (segmentation appelée sous-segmentation) et montrent que leur algorithme produit une segmentation optimale.
Nous avons adapté cet algorithme aux cartes topologiques 2D et 3D, en modifiant les critères de contraste pour les rendre plus facilement calculables [DD08b]. Pour cela, nous avons transformé le contraste externe Ext(R1,R2) en un contraste associé à chaque face de la carte Ext(f). Nous avons prouvé que le contraste externe entre R1 et R2 est égal au plus petit des contrastes de toutes les faces entre ces deux régions. Avec cette modification, nous pouvons associer chaque contraste externe aux faces de la carte topologique, et chaque contraste interne aux régions. De ce fait, étant donné un brin, nous retrouvons en O(1) ces deux valeurs.
L’Algorithme 7.2 présente la segmentation d’une image par critère de contraste à l’aide d’une carte topologique. Il prend en paramètre une carte topologique M représentant une sur-segmentation d’une image et modifie la carte afin que la partition représentée soit optimale. Cet algorithme est donné ici en 3D mais est directement modifiable en dimension n, en remplaçant β3(b) par βn(b), et en associant le contraste externe aux (n−1)-cellules. Nous avons également prouvé dans [DD08b] que cet algorithme est équivalent à l’algorithme original.
Figure 7.17: Algorithme : Segmentation par critère de contraste
- Entrées : Une carte topologique 3D M.
- Résultat : M représente la segmentation optimale de l’image.
L ← liste triée des faces;
Tant que L n’est pas vide faire
b ← défiler L;
f ← face(b);
R1 ← region(b); R2 ← region(β3(b));
Si R1 ≠ R2 alors
Si Ext(f) ≤ MInt(R1,R2) alors
R ← fusionner symboliquement R1 et R2;
Int(R) ← Ext(f);
fusion effective des régions dans la carte topologique;
Cet algorithme utilise l’opération de fusion globale évoquée Section 4.5.2, la seule différence porte sur l’initialisation des arbres union-find qui est réalisée au moyen des critères de contraste. Cet algorithme montre à nouveau l’intérêt des cartes topologiques qui autorisent la manipulation de différentes cellules (ici les régions et les faces entre les régions) en décrivant les relations d’adjacence et d’incidence entre ces cellules. Nous avons intégré cette méthode à nos deux logiciels permettant de calculer les cartes topologiques 2D et 3D à partir d’images (cf. Fig. 7.18 pour une capture d’écran du logiciel 3D) et effectué plusieurs expérimentations afin d’étudier l’efficacité de notre approche. Ces résultats montrent en moyenne que la segmentation d’une image 3D de taille 256×256×93 est réalisée en 13 secondes ce qui est tout à fait raisonnable sachant que le logiciel développé est pour le moment un prototype et pourrait bénéficier de nombreuses optimisations.
De plus, nous avons proposé des variantes de cet algorithme, en modifiant simplement le critère utilisé pour autoriser la fusion, afin par exemple de proposer un algorithme fusionnant chaque région de taille inférieure à un seuil donné avec la région la plus proche dans son voisinage. Cette opération permet de supprimer rapidement toutes les petites régions obtenues après une passe de segmentation, qui sont souvent issues de bruit.
Nous avons proposé dans [DD09] une variante particulièrement intéressante, et justifiant l’intérêt d’un modèle topologique, qui consiste à intégrer un critère topologique à l’algorithme de segmentation. Nous avons pour cela utilisé la méthode de calcul des nombres de Betti des régions de la carte topologique présenté Section 6.3, et avons montré comment utiliser ces nombres de Betti au sein du critère de segmentation. Notre idée est de contrôler l’évolution des nombres de Betti durant la segmentation afin de guider le résultat en fonction de connaissance a-priori. Un exemple d’utilisation pourrait être la segmentation du cortex cérébral sur les images IRM, où un résultat connu en médecine dit que chaque hémisphère du cortex est homéomorphe à une sphère sans cavité. En intégrant un critère topologique basé sur les nombres de Betti, nous pouvons garantir que le résultat produit par la segmentation vérifie cette propriété.
Pour mettre en place ce contrôle, nous conservons le même algorithme de segmentation que nous venons de présenter, en modifiant simplement le critère utilisé lors de la fusion symbolique. Durant l’exécution de cet algorithme, pour chaque face courante incidente à R1 et R2, nous effectuons les quatre étapes suivantes :
Le premier test utilise un critère valeur classique, par exemple celui à base des contrastes, afin de fusionner des zones homogènes de l’image. Lorsque ce critère est satisfait, nous calculons les nombres de Betti de la région que nous obtiendrions comme résultat de la fusion en utilisant la méthode de mise à jour locale, et vérifions si le critère topologique sur cette éventuelle future région est satisfait. Lorsque c’est le cas, la fusion symbolique est réalisée.
Nous avons proposé différents types de critères topologiques, qui peuvent contrôler l’évolution des tunnels avec b1 et/ou des cavités avec b2. Ces critères peuvent être :
Il est simple de définir d’autres critères, voire de combiner les deux nombres de Betti afin par exemple d’autoriser les objets pour lesquels la somme des nombres de tunnels et de cavités est inférieure à un seuil donné.
Afin de réaliser ce critère topologique, nous calculons les nombres de Betti de R1 ∪ R2 au cours de l’étape de la fusion symbolique, sans réaliser effectivement cette fusion, ce qui est beaucoup plus efficace. Par contre, cela demande à modifier le parcours de surface utilisé lors de la mise à jour locale des nombres de Betti afin de parcourir les régions résultantes de la fusion symbolique. Il suffit pour cela de traverser également les brins des faces internes des régions, c’est-à-dire les faces incidentes à un brin b tel que find(region(b))=find(region(β3(b))). Traverser ces faces revient à parcourir le chemin de connexion entre les brins situés autour de celles-ci, ce qui nous ramène bien au parcours des brins de la surface obtenue après la suppression des faces internes.
Nous avons effectué plusieurs tests afin d’étudier l’impact du critère topologique sur le résultat de segmentation. Nous pouvons voir Fig. 7.19 un exemple obtenu avec une image artificielle en utilisant un critère topologique interdisant à b1 de dépasser un certain seuil. Nous voyons sur cet exemple l’impact du critère topologique qui entraîne différents résultats. Comme ici le critère utilisé interdit strictement à b1 de dépasser le seuil, nous garantissons que chaque région du résultat a bien un b1 inférieur ou égal au seuil. Ce résultat dépend toutefois de la partition initiale. En effet, il est garanti uniquement si chaque région de la carte initiale est homéomorphe à une boule sans cavité. Si ce n’est pas le cas, nous ne pourrons pas, avec cette méthode, garantir de propriétés sur chaque région.
[a][b]
[c]
[d]

Figure 7.19: Expériences avec une image 3D artificielle, en utilisant un critère topologique interdisant à b1 de dépasser un certain seuil k (la région de fond n’est pas représentée afin d’observer ce qui se passe sur la région claire). Figure 7.2 Image originale. Chaque voxel de l’image appartient à une région différente. Figure 7.2 Résultat avec k=0. L’objet est représenté par trois régions, chacune n’ayant pas de tunnel. Figure 7.2 Résultat avec k=1. L’objet est représenté par deux régions, une ayant un tunnel, l’autre non. Selon l’ordre des fusions (qui dépend de la couleur des voxels) nous aurions pu obtenir deux régions sans tunnel, ou deux régions à un tunnel. Figure 7.2 2-tore obtenu lorsque nous n’utilisons pas de contrainte sur les nombres de Betti.
Nous avons utilisé les pyramides généralisées afin de mettre en place un outil de segmentation multi-échelle d’images 3D [SD06]. La construction d’une telle pyramide se base sur le même principe que celui utilisé lors de la définition des cartes topologiques 3D pour simplifier une carte en sa forme minimale, ainsi que sur l’algorithme de segmentation d’une carte présenté section précédente. L’intérêt de conserver plusieurs niveaux de segmentation d’une même image est de pouvoir ensuite travailler en parallèle sur plusieurs niveaux de segmentation différents, de choisir la segmentation la plus adaptée à l’opération effectuée, ou d’effectuer un traitement préliminaire sur une segmentation relativement grossière qui va donc demander moins de ressources, puis de concentrer les traitements de manière locale sur une segmentation plus fine.
La pyramide de cartes généralisées utilisée dans le cadre de la segmentation multi-échelle d’une image 3D représente chaque niveau de segmentation et permet une navigation entre les niveaux de segmentation mais aussi entre les cellules les composant. La construction de cette pyramide est réalisée à partir d’une première carte qui représente soit chaque voxel de l’image dans sa propre région, soit qui est une pré-segmentation de l’image initiale en un grand nombre de régions. Le choix de la méthode initiale dépendra de la taille des images à traiter et du niveau de bruit.
Ensuite, l’ajout d’un nouveau niveau de segmentation est obtenu en trois étapes :
En n’effectuant qu’un seul type de suppression à la fois, l’ajout d’un k-ième niveau de segmentation d’une image est réalisé par l’ajout de trois nouveaux niveaux dans la pyramide :
La pyramide permettant de représenter différents niveaux de segmentation d’une même image 3D peut être définie formellement de la manière suivante.
Le critère de segmentation utilisé pour construire chaque nouveau niveau de segmentation peut-être celui présenté à la section précédente basé sur les contrastes ou un autre, et il peut éventuellement intégrer un critère de contrôle topologique. En effet, tout les travaux présentés dans les chapitres précédents (calcul des cartes topologiques et des invariants topologiques) s’étendent directement aux pyramides puisque chaque niveau est une carte généralisée. De plus, ces travaux peuvent souvent être optimisés en utilisant le modèle hiérarchique afin de propager les calculs et simplifier les opérations et les parcours. Nos expérimentations de segmentation hiérarchique 3D se sont pour le moment limitées à des images artificielles de très faibles tailles, afin de tester et valider les algorithmes. Ces travaux autour de l’utilisation de ces pyramides doivent être poursuivis et étendus afin de pouvoir traiter des images réelles de taille plus importante, et de définir des méthodes de traitement d’images hiérarchiques.
Dans ce chapitre, nous avons présenté différentes utilisations des cartes et des extensions présentées tout au long de ce mémoire. Nos champs privilégiés d’expérimentation sont la modélisation géométrique et le traitement d’images. Ces deux thématiques de recherche, a priori relativement éloignées, se rejoignent dans les besoins de décrire des objets, les cellules des subdivisions, et les relations d’incidence et d’adjacence entre les cellules. De plus, les opérations spécifiques développées dans des applications précises se rejoignent souvent dans l’utilisation d’opérations de base communes (par exemple les opérations de suppression), et dans les besoins de contrôler l’évolution des objets durant ces simplifications. Nous avons par exemple pu voir que le problème de déconnexion se produisant dans le cadre de la reconstruction de complexes architecturaux est résolu par l’adjonction d’arêtes fictives qui est la solution utilisée pour résoudre le même problème dans les cartes topologiques 3D.
Nous avons également vu dans ce chapitre comment mettre en œuvre un processus de segmentation d’images à l’aide des cartes topologiques. Dans un premier temps, nous avons simplement porté un algorithme existant sur les graphes. Mais nos travaux trouvent leur pleine justification dans l’utilisation d’un critère topologique au sein de l’algorithme de segmentation. En effet, mettre en place ce critère nécessite d’être capable de calculer efficacement, donc localement, l’évolution des caractéristiques topologiques étudiées, ce qui est possible ici grâce à l’utilisation d’un modèle à base de carte décrivant la topologie de la subdivision.
Nous avons également utilisé les cartes combinatoires dans différentes autres applications. Nous pouvons citer un algorithme de remplissage de l’intérieur de régions [DA07], une méthode de reconstruction parallèle de contours discrets multi-régions [DC08], ou encore des méthodes de segmentation d’images 2D par approches stochastiques à base de chaînes de Markov [BAD+02, DAB03]. Dans chacun de ces cas, les cartes permettent de manipuler la subdivision des objets manipulés, d’associer des informations aux cellules (comme par exemple des équations de droites discrètes aux arêtes pour la reconstruction parallèle de contours discrets), et d’utiliser des critères topologiques (comme par exemple la profondeur dans l’arbre d’imbrication pour le remplissage de l’intérieur de régions).
Les poursuites possibles de ces travaux sont nombreuses et les perspectives très riches. Tout d’abord dans le cadre de la modélisation, nous souhaitons étudier le lien entre les pyramides de cartes et les opérations de modélisation, afin de pouvoir, à long terme, proposer un modeleur géométrique qui devrait être l’équivalent de Moka, mais totalement hiérarchique. Pour cela, nous devons étudier chaque opération et définir quel est le résultat à produire dans le cas hiérarchique. L’intérêt de ce type d’opération réside à nouveau dans les optimisations possibles en effectuant certains calculs à une faible résolution puis en propageant ces informations de proche en proche dans les niveaux de la pyramide.
Ces perspectives sont plus importantes concernant le traitement d’images. En effet, nous avons pour le moment proposé un premier critère topologique de contrôle de segmentation, et ce travail doit être poursuivi et développé afin de montrer pleinement son intérêt dans des problématiques réelles. Pour cela, nous devons travailler en collaboration avec des spécialistes de traitement d’images, et nous atteler à la résolution de problèmes concrets dans lesquels nous sommes convaincus que l’apport d’information topologique peut aider à améliorer le résultat obtenu. De plus, nous pouvons également envisager de proposer de nouvelles opérations utiles dans le cadre du traitement d’images. Nous souhaitons développer de nouveaux critères de segmentation, utilisant par exemple des critères géométriques sur la taille ou la forme des frontières entre les régions, mais aussi des nouvelles opérations semi-interactives afin de permettre à un expert de corriger simplement le résultat d’une segmentation qu’il ne trouverait pas satisfaisant. Ce type d’opération rejoint partiellement les opérations de modélisation géométrique, tout en rajoutant un contrôle supplémentaire lié au fait que l’espace sous-jacent est discret. Nous envisageons par exemple une opération de découpe d’une région 3D, qui serait guidée par la souris de l’expert mais également par les données images, par exemple en utilisant une image de gradient, tout en ajoutant un contrôle topologique. Ces travaux peuvent être très nombreux et trouver des débouchés importants, mais nécessitent des collaborations avec des spécialistes afin de répondre à des problématiques précises.
Une dernière perspective de recherche qui est relativement récente concerne l’intégration d’un noyau de cartes combinatoires dans la CGAL (Computational Geometry Algorithms Library, cf. http://www.cgal.org/), une bibliothèque très importante de géométrie algorithmique. Cette bibliothèque très riche permet pour le moment, entre autres, de manipuler des triangulations 2D et 3D, et des subdivisions cellulaires 2D à l’aide d’une structure de demi-arêtes, mais il n’existe pas de structure pour les subdivisions cellulaires 3D ce qui peut s’avérer limitant pour ses utilisateurs. Nous avons donc commencé à développer un noyau de cartes combinatoires pouvant s’intégrer dans CGAL, en utilisant l’expérience acquise durant le développement de Moka et des deux programmes autour des cartes topologiques 2D et 3D. Notre premier objectif est de proposer assez rapidement un noyau permettant de manipuler des subdivisions nD à l’aide de n-cartes, puis par intégrer progressivement des opérations de manipulation et de calcul d’invariants topologiques.
Dans ce mémoire nous avons résumé nos principales contributions autour des cartes combinatoires et cartes généralisées qui sont : la définition générique des quatre opérations de base, la définition des cartes topologiques 2D et 3D, la définition des pyramides généralisées, le calcul d’invariants topologiques, et l’utilisation de ces résultats dans différentes applications.
Nous avons tout d’abord défini les quatre opérations de base, génériques et en dimension quelconque qui sont la suppression, la contraction, l’insertion et l’éclatement. Ces opérations peuvent être considérées comme la généralisation des opérateurs d’Euler, tout en jouant un rôle de factorisation puisque ces quatre opérations de base recouvrent et généralisent les nombreux opérateurs d’Euler 2D existants. Nous avons également défini l’opération de décalage d’arête, mais pour le moment uniquement en 2D et 3D. Ces opérations, et principalement l’opération de suppression, sont au cœur de nos travaux et servent dans différentes utilisations très diverses, allant de la segmentation d’images avec contraintes topologiques au calcul des générateurs des groupes d’homologie.
Nous avons ensuite défini les cartes topologiques en 2D et 3D, qui généralisent et étendent les travaux précédents autour de la définition de modèles topologiques de représentation de partitions d’images. Les définitions utilisent les opérations de base, et l’introduction du concept de niveau de simplification facilite l’étude de ces modèles en découpant les problèmes. Nous avons montré que ces cartes topologiques sont un bon outil pour manipuler les partitions d’images et pour définir ensuite des opérations de plus haut niveau.
Nous nous sommes également intéressés aux pyramides généralisées qui sont une extension hiérarchique permettant de manipuler au sein d’une même structure différentes résolutions d’une même carte. Nous avons défini cette structure à nouveau de manière générique en dimension quelconque, sans contrainte additionnelle sur les opérations utilisés pour la construction. Cela autorise différentes utilisations possibles, en ajoutant si besoin des contraintes supplémentaires. Nous avons ensuite étudié comment les informations pouvaient être retrouvées à travers les différents niveaux de la pyramide. Nous avons pour cela introduit la notion d’orbite généralisée, et montré que sous certaines conditions nous avions des propriétés intéressantes sur les cellules généralisées qui sont associées aux cellules.
Nous avons également étudié différentes méthodes de calcul d’invariants topologiques permettant de calculer la caractéristique d’Euler-Poincaré, les nombres de Betti, et les groupes d’homologie. Pour ces deux derniers invariants, nous avons pour le moment uniquement des résultats en 2D et 3D, et l’extension en dimension supérieure est une de nos perspectives de recherche. Pour ces algorithmes, nous avons proposé lorsque c’est possible une version permettant de calculer localement la mise à jour de ces invariants lors des opérations de simplification. Cela nous a permis de proposer une méthode de contrôle topologique des opérations de fusion que nous avons utilisée ensuite afin de contrôler l’évolution des nombres de Betti des régions obtenues au cours de l’application d’un algorithme de segmentation d’images 3D.
Enfin nous avons présenté différentes utilisations de nos travaux, principalement un projet de reconstruction de complexes architecturaux à partir de plans numériques, et des méthodes de segmentation d’images 2D et 3D. Ces différentes utilisations illustrent différentes possibilités applicatives, tout en montrant également l’intérêt d’avoir des opérations de base génériques puisqu’elles servent ensuite dans des cadres très différents.
Notre programme de recherche consiste à continuer d’enrichir les modèles à base de cartes de nouvelles opérations, en nous concentrant sur l’étude et le contrôle des propriétés topologiques, et à utiliser ces résultats théoriques au sein d’applications de traitement d’images et de modélisation géométrique. De plus, ces travaux peuvent être à chaque fois menés dans le cadre mono-échelle et multi-échelle. À long terme, notre objectif est de définir un cadre complet permettant la mise en place rapide de nouvelles méthodes, tant du point de vue théorique en s’appuyant sur des opérations de base génériques, prouvées, et autorisant un contrôle précis, que pratique, en utilisant des bibliothèques existantes et leurs fonctionalités.
Pour atteindre cet objectif, il reste à étendre plusieurs travaux présentés dans ce mémoire afin de les généraliser en dimension quelconque. C’est le cas de la définition de la carte topologique pour laquelle le principe des niveaux de simplification est déjà valide en dimension quelconque, mais pour laquelle il reste à étudier la définition de cellules fictives et leur décalage. En effet ces opérations existent pour le moment seulement pour les arêtes, et posent encore des problèmes dans le cas général.
C’est le cas également pour le calcul des nombres de Betti et des groupes d’homologie qui sont pour le moment uniquement définis en 2D et 3D. Pour atteindre cet objectif, nous avons déjà défini un opérateur de bord sur les G-cartes en dimension quelconque, et avons des premiers résultats non encore publiés mais très prometteurs sur son utilisation permettant de calculer les matrices d’incidences des cellules de la carte. De plus, nos premières expérimentations montrent un fort intérêt à coupler ces méthodes avec une passe de simplification utilisant les opérations de suppression pour diminuer à la fois les temps de calcul, et l’espace mémoire occupé par les matrices. Mais pour cela, nous devons étudier le lien entre les opérations de réduction sur les ensembles simpliciaux, et les opérations de suppression et contraction. En effet, il a été prouvé que ces opérations de réductions préservent l’homologie, et ce lien nous permettrait de prouver la propriété équivalente pour nos opérations.
Nous souhaitons également étudier plus précisément la notion de schéma polyédrique pour voir s’il est possible d’étendre nos méthodes de calcul de schéma polygonal en dimension supérieure. Cela rejoint une autre problématique théorique qui est sous-jacente à de nombreuses parties de nos travaux et qui est la caractérisation combinatoire des boules. En effet, différents algorithmes fonctionnent uniquement si les cellules de la subdivision sont des boules. Nous savons garantir cette contrainte si les objets sont orientables et de dimension 3, et lorsque la subdivision initiale vérifie cette contrainte, ce qui est le cas dans le cas des subdivisions cubiques des images 3D. Mais il serait très intéressant d’être capable de caractériser cette propriété pour vérifier si une carte donnée la respecte ou non. Cela semble un sujet ouvert très difficile, mais les pistes évoquées lors de la présentation de la caractéristique cellulaire d’Euler-Poincaré dans le cadre des G-cartes doivent être creusées.
Nous allons également étudier la possibilité d’étendre les opérations de base en relâchant les contraintes de cellules disjointes. Notre objectif est ici de pouvoir simplifier plus rapidement une carte. Cela fournirait une optimisation en temps de calcul puisque plusieurs passes pourraient alors être regroupées en une seule. Mais cela fournirait surtout une optimisation en espace mémoire dans le cadre des pyramides de cartes, en diminuant le nombre de niveaux nécessaires puisque plusieurs niveaux seraient regroupés en un seul. Ce dernier point est crucial pour que les pyramides puissent être utilisées dans des applications 3D réelles. La problématique est ici de garantir qu’il n’y a pas de perte d’information, c’est-à-dire qu’il est possible après l’opération de retrouver correctement les chemins de connexion entre les brins survivants, ainsi que les notions d’orbites généralisées.
Dans le cadre des cartes topologiques, nous devons maintenant valider nos méthodes au sein d’applications réelles de traitement d’images. Il faudra pour cela travailler en collaboration avec des spécialistes de traitement d’images pour résoudre des problèmes spécifiques et précis. Cela nous permettra de paramétrer nos algorithmes dans ces objectifs, en utilisant le contrôle topologique, et d’éventuelles opérations semi-automatiques. Nous attendons également de ce travail un retour nous permettant de mieux cerner les besoins en applications réelles, tant au niveau de nouvelles opérations, qu’au niveau des temps de calcul ou pour le contrôle topologique.
Toujours dans ce cadre, nous souhaitons étudier les opérations de bas niveaux travaillant sur les pixels/voxels de l’image, en commençant par la modification de la région d’un pixel/voxel. Ce type d’opération n’est pas simple à intégrer car la carte topologique représente les régions, donc les ensembles de pixels/voxels, mais l’accès et la modification des pixels/voxels n’est pas immédiat. Il est important de fournir également ce type d’opérations pour qu’un utilisateur puisse modifier directement les images en fonction de ses besoins. À partir de ces opérations, nous pouvons ensuite étudier différentes opérations qui s’appuient sur ces opérations de base comme par exemple des opérations de morphologie mathématique, de squelettisation ou encore des calculs de distances. Pour ces opérations, il peut être intéressant d’étudier l’apport d’un modèle global de représentation qui va permettre de calculer des informations rapidement sur la surface des objets. Dans ce cadre nous avons commencé à travailler sur un modèle déformable discret multi-étiquette [DDL09, DDL10] qui permet de modifier localement la géométrie d’une partition tout en préservant sa topologie. Enfin, à l’autre bout de la chaîne, nous devons poursuivre le développement d’opérations de haut niveau de traitement d’images, en profitant des spécificités de nos modèles pour guider les opérations et de les contrôler.
Un autre point de recherche, qui est totalement nouveau, concerne l’étude d’outils de comparaison de cartes. En effet, la seule opération qui existait jusqu’à présent pour comparer deux cartes était le test d’isomorphisme, ce qui est très limitant. Notre objectif est ici de proposer des outils permettant de comparer des cartes, par exemple pour savoir si deux cartes sont similaires ou au contraire totalement différentes. Nous avons donc débuté récemment des travaux autour de la définition ce type d’outils. Nous avons tout d’abord défini un algorithme de détection de sous-isomorphisme entre cartes [DdlHJ+09b, DdlHJ+09a] qui est polynomial. Nous avons également proposé une signature de cartes combinatoires qui permet une recherche polynomiale d’une carte dans une base de cartes [GDS09]. Nous poursuivons maintenant ces travaux autour de deux axes, dans le cadre de deux thèses co-encadrées avec Christine Solnon. Le premier axe, dans le cadre de la thèse de Stéphane Gosselin, concerne la fouille de données dans une base de cartes, où l’objectif est de rechercher la présence de motifs fréquents dans la base (un motif fréquent est une sous-carte apparaissant dans un suffisamment grand nombres de cartes de la base). Le second axe, dans le cadre de la thèse de Camille Combier, concerne la définition de mesure de similarité entre cartes. Cette mesure peut être vue comme une distance permettant de quantifier la similarité des cartes. Nous souhaitons ensuite utiliser cette mesure pour définir une distance d’édition calculant le nombre minimal d’opérations de base pouvant transformer une carte dans une autre. Ces travaux débutent juste mais nos premiers résultats sont très encourageants et montrent que la structure combinatoire et ordonnée des cartes nous permet de définir des algorithmes gloutons, là où il faut des recherches plus complexes avec des graphes étant donné que les arêtes ne sont pas ordonnées autour des sommets. Ces travaux doivent être réalisés de manière théorique et générique en dimension quelconque, puis de manière appliquée en s’attaquant à la résolution d’une problématique précise en utilisant ces nouveaux outils.
Enfin, les deux dernières perspectives de recherche sont très vastes, et pas du tout abordées pour le moment. La première perspective concerne l’étude de cartes permettant de représenter des partitions pouvant se chevaucher. Ce type de carte pourrait être intéressant, par exemple pour représenter des zones de flou au bord des régions, ou encore pour assigner plusieurs labels apportant des informations différentes à une même région. La problématique est ici complexe car le modèle même des cartes est très lié à la représentation des subdivisions. La seconde perspective concerne l’utilisation des cartes topologiques dans des images animées 2D ou 3D plus temps. En théorie, comme les cartes combinatoires sont définies en dimension quelconque, la représentation de ce type d’objet doit pouvoir de faire sans problème. En pratique, nous devons étudier l’impact de la non homogénéité dans les dimensions sur les opérations et sur les calculs des caractéristiques. Ce type de modèle ouvre des perspectives très intéressantes. Nous envisageons par exemple de faire du suivi d’objet, où une occlusion à un certain moment qui s’arrête plus tard pourrait correspondre à un tunnel ayant un générateur temporel.
Pour pouvoir aboutir, ces travaux doivent être menés en collaboration avec d’autres chercheurs, et dans le cadre de différents projets. Nous souhaitons pour cela poursuivre les collaborations existantes, mais également créer des nouveaux liens avec des spécialistes de traitement d’images concernant nos travaux autour de l’imagerie, ou de topologie algébrique pour les aspects liés aux invariants topologiques. Dans cet objectif, nous envisageons le dépôt d’un projet européen «Homology-based Discrete Image Processing» en collaboration avec le laboratoire XLIM-SIC de Limoges, le laboratoire CATAM de Séville, en Espagne, et le laboratoire PRIP de Vienne, en Autriche. Nous avons également participé au montage du projet «DigitalSnow: Géométrie discrète et mathématiques appliquées pour la métamorphose de neige», en collaboration avec le LAMA de Chambéry et le CEN de Grenoble, soumis à l’appel 2010 des programmes blanc de l’ANR. Enfin, nous sommes également impliqué dans le projet de David Coeurjolly «GigaSpel: Digital Geometry for High Performance n-D Image Analysis» soumis à l’ERC Starting Grant 2010. Ces trois projets tournent autour des problématiques liées à la représentation efficace d’objets 3D, 4D ou nD, à la définition d’opérations de manipulation, au calcul d’invariants topologiques, et à l’utilisation de tous ces outils dans la résolution de problématiques spécifiques. Ils illustrent bien la richesse de nos travaux, et les différentes possibilités de recherche tant au niveau théorique que pratique.
En effet, l’étude de toutes ces perspectives de recherches doit être menée conjointement de manière théorique et générique, de manière spécialisée afin de proposer des méthodes efficaces et éventuellement spécialisées, mais s’appuyant sur les bases fondamentales, et de manière pratique en implémentant et testant nos méthodes au sein de différents logiciels.
|
|
Ce document a été traduit de LATEX par HEVEA