Constructing an n-dimensional cell complex from a soup of (n-1)-dimensional faces

Arroyo Ohori K., Damiand G., Ledoux H.

Proc. of 1st International Conference on Applied Algorithms (ICAA)
Lecture Notes in Computer Science 8321, pages 37-48, January 2014, Kolkata, India

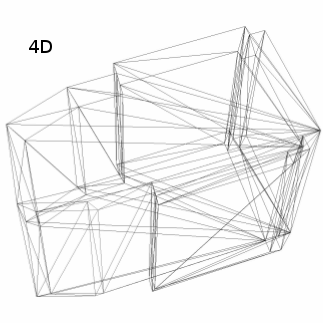
Abstract: There is substantial value in the use of higher-dimensional (>3D) digital objects in GIS that are built from complex real-world data. This use is however hampered by the difficulty of constructing such objects. In this paper, we present a dimension independent algorithm to build an n-dimensional cellular complex with linear geometries from its isolated (n-1)-dimensional faces represented as combinatorial maps. It does so by efficiently finding the common (n-2)-cells (ridges) along which they need to be linked. This process can then be iteratively applied in increasing dimension to construct objects of any dimension. We briefly describe combinatorial maps, present our algorithm using them as a base, and show an example using 2D, 3D and 4D objects which was verified to be correct, both manually and using automated methods.

Keywords: n-D reconstruction; GIS; Combinatorial maps.

BibTex references

@InProceedings{ADL14,
      author = {{Arroyo Ohori}, K. and {Damiand}, G. and {Ledoux}, H.},
      title = {Constructing an n-dimensional cell complex from a soup of (n-1)-dimensional faces},
      booktitle = {Proc. of 1st International Conference on Applied Algorithms (ICAA)},
      series = {Lecture Notes in Computer Science},
      publisher = {Springer International Publishing},
      volume = {8321},
      pages = {37-48},
      month = {January},
      year = {2014},
      address = {Kolkata, India},
      keywords = {n-D reconstruction; GIS; Combinatorial maps.},
      url = {https://doi.org/10.1007/978-3-319-04126-1_4}
}

Guillaume Damiand

Constructing an n-dimensional cell complex from a soup of (n-1)-dimensional faces

Links:

BibTex references

Image