2D Topological Map Isomorphism for Multi-label Simple Transformation Definition

Damiand G., Roussillon T., Solnon C.

Proc. of 18th International Conference on Discrete Geometry for Computer Imagery (DGCI)
Lecture Notes in Computer Science 8668, pages 39-50, September 2014, Siena, Italy

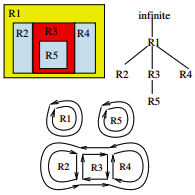
Abstract: A 2D topological map allows one to fully describe the topology of a labeled image. In this paper we define 2D topological map isomorphism. We show that isomorphic topological maps correspond to homeomorphic embeddings in the plane and we give a polynomial-time algorithm for deciding of topological map isomorphism. Then we use this notion to give a generic definition of multi-label simple transformation as a set of transformations of labels of pixels which does not modify the topology of the labeled image. We illustrate the interest of multi-label simple transformation by generating look-up tables of any pair of adjacent pixel transformation preserving the topology.

Keywords: Combinatorial maps; 2D topological maps isomorphism; Labeled image; Simple points; Simple sets.

BibTex references

@InProceedings{DRS14,
      author = {{Damiand}, G. and {Roussillon}, T. and {Solnon}, C.},
      title = {2D Topological Map Isomorphism for Multi-label Simple Transformation Definition},
      booktitle = {Proc. of 18th International Conference on Discrete Geometry for Computer Imagery (DGCI)},
      series = {Lecture Notes in Computer Science},
      publisher = {Springer International Publishing},
      volume = {8668},
      pages = {39-50},
      month = {September},
      year = {2014},
      address = {Siena, Italy},
      keywords = {Combinatorial maps; 2D topological maps isomorphism; Labeled image; Simple points; Simple sets.},
      url = {https://doi.org/10.1007/978-3-319-09955-2_4}
}

Guillaume Damiand

2D Topological Map Isomorphism for Multi-label Simple Transformation Definition

Links:

BibTex references

Image