Persistent Homology Computation Using Combinatorial Map Simplification

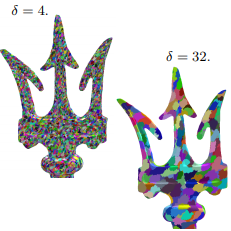
Abstract: We propose an algorithm for persistence homology computation of orientable 2-dimensional (2D) manifolds with or without boundary (meshes) represented by 2D combinatorial maps. Having as an input a real function h on the vertices of the mesh, we first compute persistent homology of filtrations obtained by adding cells incident to each vertex of the mesh, The cells to add are controlled by both the function h and a parameter delta. The parameter delta is used to control the number of cells added to each level of the filtration. Bigger delta produces less levels in the filtration and consequently more cells in each level. We then simplify each level (cluster) by merging faces of the same cluster. Our experiments demonstrate that our method allows fast computation of persistent homology of big meshes and it is persistent-homology aware in the sense that persistent homology does not change in the simplification process when fixing delta.

Keywords: Persistent homology computation; 2D combinatorial map; mesh simplification.