Home page
Home page Researches
Researches Publications
Publications Teaching
Teaching Supervised Thesis
Supervised Thesis CV
CV Contacts
ContactsRasterized Planar Face Complex
Computer-Aided Design (CAD)
Volume 90, pages 146-156, September 2017
Volume 90, pages 146-156, September 2017
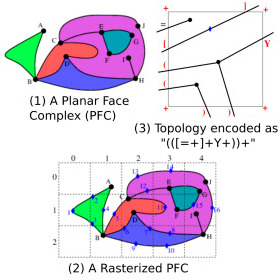
Abstract: We consider a Planar Face Complex (PFC). It is defined by the immersion of a planar and connected graph G, which comprises a set of vertices joined by curved edges. G decomposes the plane into faces that need not be manifold or open-regularized and may be bounded by a single loop edge. The PFC may, for example, be used to represent the complex street network of a city, the decomposition of a continent into countries, or the inhomogeneous structure made of a large set of regions of different materials possibly with internal cracks. The rasterized Planar Face Complex (rPFC) proposed here provides a compact representation of an approximation of a PFC, where the precise location of each vertex is quantized to the pixel that contains it and where the precise geometry of each curved edge is approximated by the ordered list (with possible repetitions) of the pixels traversed by (a chosen polygonal approximation of) the edge. We claim three key contributions: (1) The geometric error between a PFC and its rPFC is bounded by the pixel half-diagonal. (2) In spite of such a drastic discretization of the geometry, the rPFC captures the exact topology of the original PFC (provided that no street lies entirely inside a single pixel) and supports standard graph traversal operators that permit to walk the loop of sidewalks along the streets that bound a face, to cross a street to the opposite sidewalk, or to cross streets in order while walking around their common junction. (3) The local connectivity and order information needed to provide the above functionality is stored at each pixel using only about 4 bits per crossing. We discuss the details of this representation, our implementation of its exact construction, four possible embodiments that offer different space/time efficiency compromises, experimental results, relations between rPFC and prior solutions.
Keywords: Planar polygonal meshes; Combinatorial maps; Compact representation; Topology preserving rasterization.
Keywords: Planar polygonal meshes; Combinatorial maps; Compact representation; Topology preserving rasterization.
BibTex references
@Article{DamRos17,
author = {Damiand, G. and Rossignac, J.},
title = {Rasterized Planar Face Complex},
journal = {Computer-Aided Design (CAD)},
publisher = {Elsevier},
volume = {90},
pages = {146-156},
month = {September},
year = {2017},
keywords = {Planar polygonal meshes; Combinatorial maps; Compact representation; Topology preserving rasterization.},
url = {https://doi.org/10.1016/j.cad.2017.05.010}
}
author = {Damiand, G. and Rossignac, J.},
title = {Rasterized Planar Face Complex},
journal = {Computer-Aided Design (CAD)},
publisher = {Elsevier},
volume = {90},
pages = {146-156},
month = {September},
year = {2017},
keywords = {Planar polygonal meshes; Combinatorial maps; Compact representation; Topology preserving rasterization.},
url = {https://doi.org/10.1016/j.cad.2017.05.010}
}
Image
 [Back]
[Back]