3D Shape Reconstruction via Optimal Transport Project
Back
This project, done during my postdoc, aims at reconstructing 3D shapes from a set of points using an optimal transportation inspired metric to guide the reconstruction.
Assuming that the set of input points is a set of Dirac masses and the mesh it is transported to as a piecewise constant measure on each triangle, the problem can be formulated as a linear problem.
Using a local relaxation (which converges to a local minium of the Optimal Transport Cost), the problem can be efficiently solved.
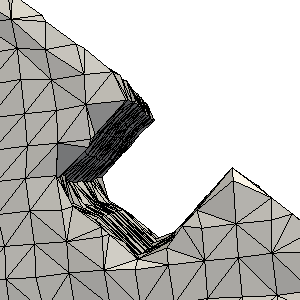
Apart from 3d reconstruction, the method can be used to recover sharp features and surface boundaries as a post-processing step after using a semi-smooth closed shape reconstruction method.
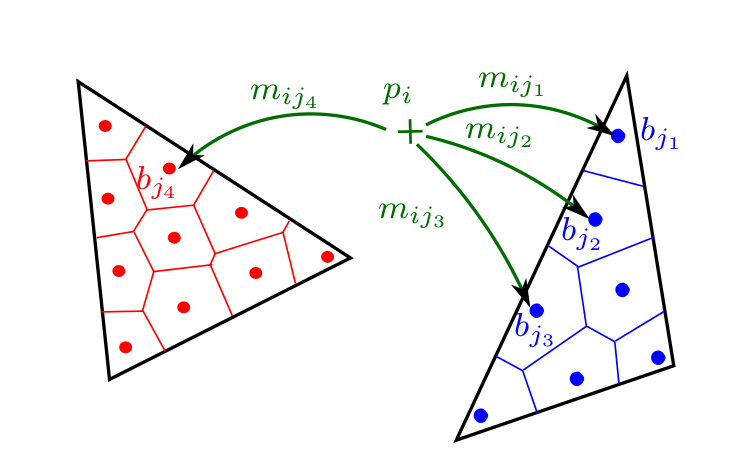
Each point pi with mass mi can be partially transported to several bin locations bj, this transportation is naturally computed so that it minimizes the transport cost (Wasserstein 2). Let s(j) be the index of the simplex containing bin bj, an cj the capacity of bin bj (proportional to the area of bin bj on simplex s(j)). Thus the program can be rewritten using variables mij (partial mass of pi transported to bin bj) with the constraints:
- Mass conservation: the total mass of the point must be transported (first constraint)
- Piecewise uniformity: each bin of a given simplex must receive the exact same mass (second constraint).
- Non-negativity of the transported mass and the mass received by the bin
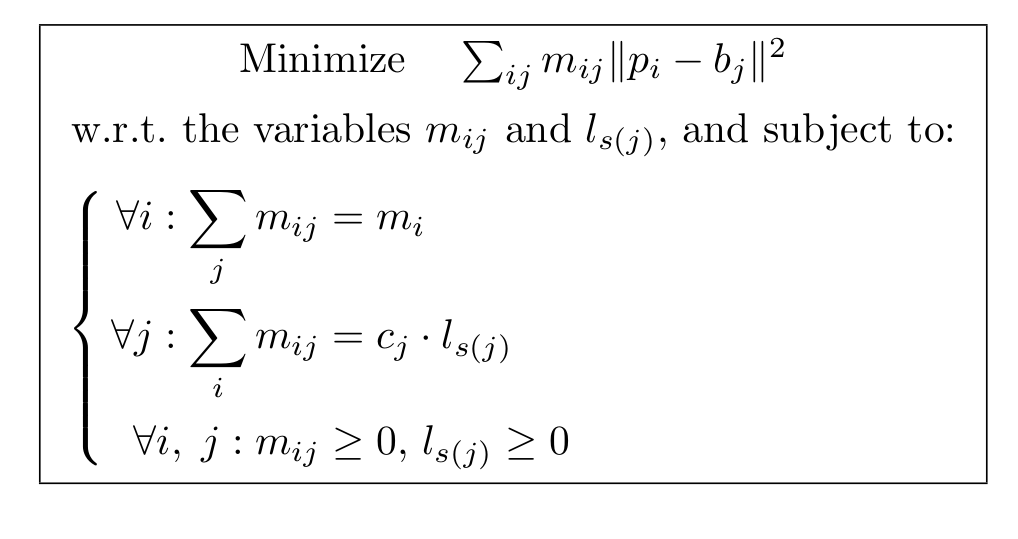
Paper: Feature-Preserving Surface Reconstruction and Simplification from Defect-Laden Point Sets
final PDF file (2013)
preprint - June 2012
Version française - communication aux GTMG 2013
Abstract of the paper
We introduce a robust and feature-capturing surface reconstruction and simplification method that turns an input point set into a low triangle-count simplicial complex. Our approach starts with a (possibly non-manifold) simplicial complex filtered from a 3D Delaunay triangulation of the input points. This initial approximation is iteratively simplified based on an error metric that measures, through optimal transport, the distance between the input points and the current simplicial complex---both seen as mass distributions. Our approach is shown to exhibit both robustness to noise and outliers, as well as preservation of sharp features and boundaries. Our new feature-sensitive metric between point sets and triangle meshes can also be used as a post-processing tool that, from the smooth output of a reconstruction method, recovers sharp features and boundaries present in the initial point set.
Some results from the paper

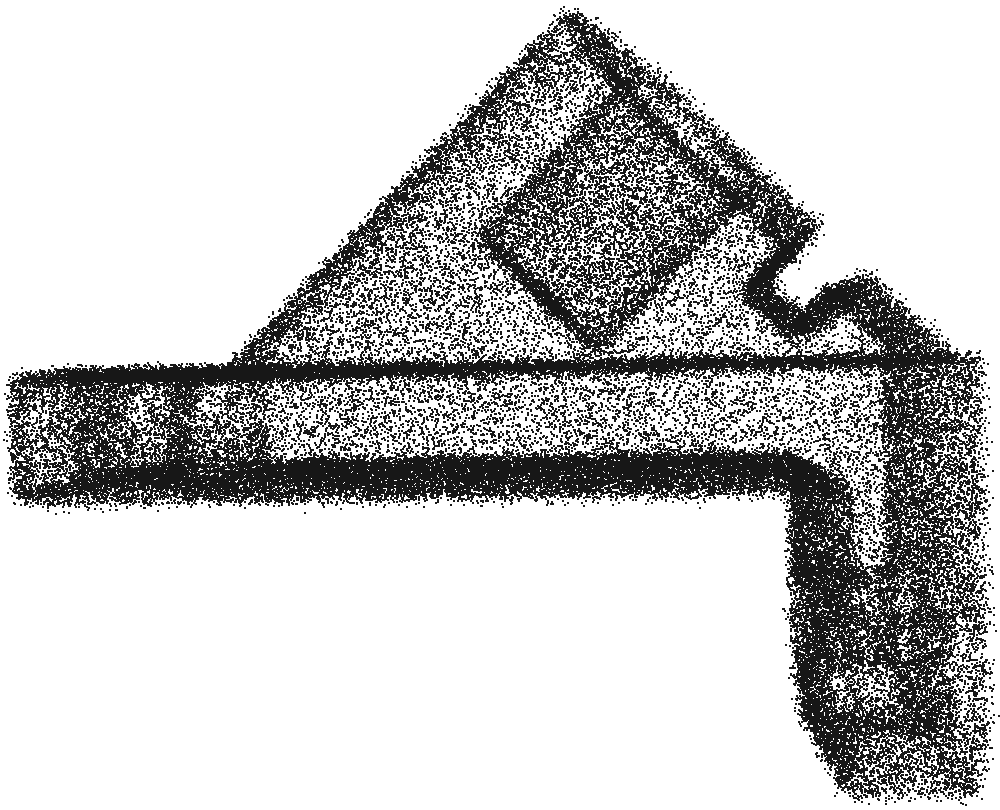
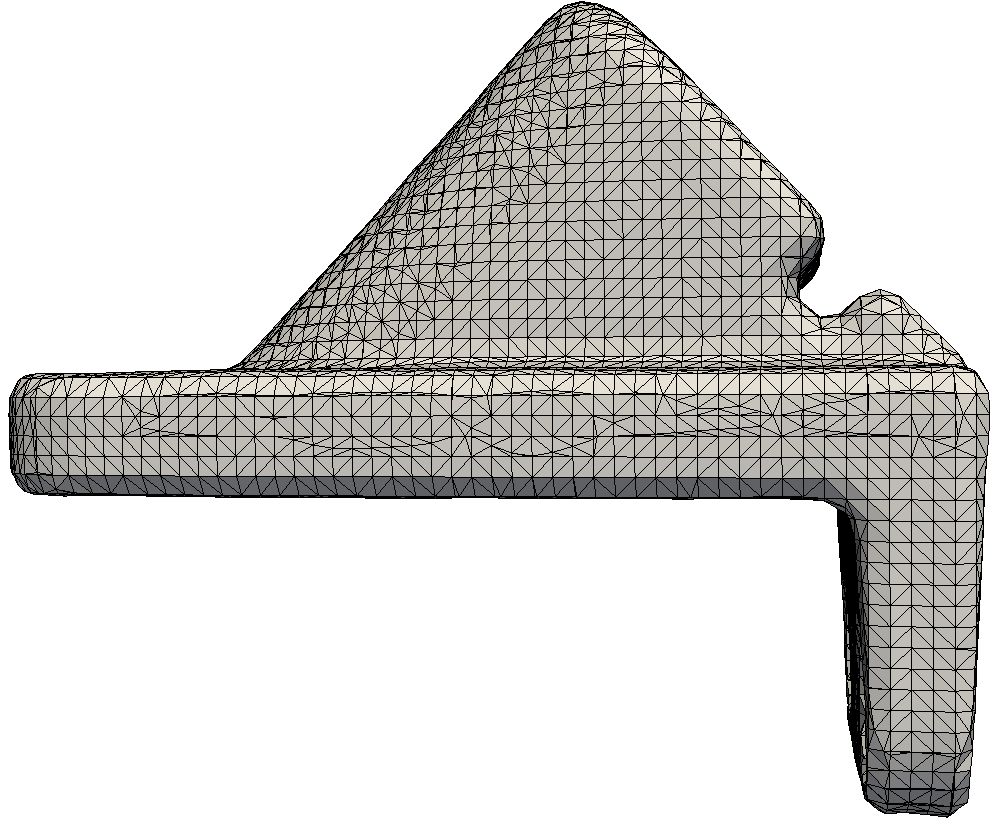
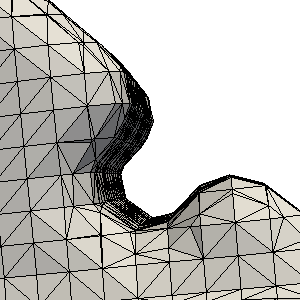
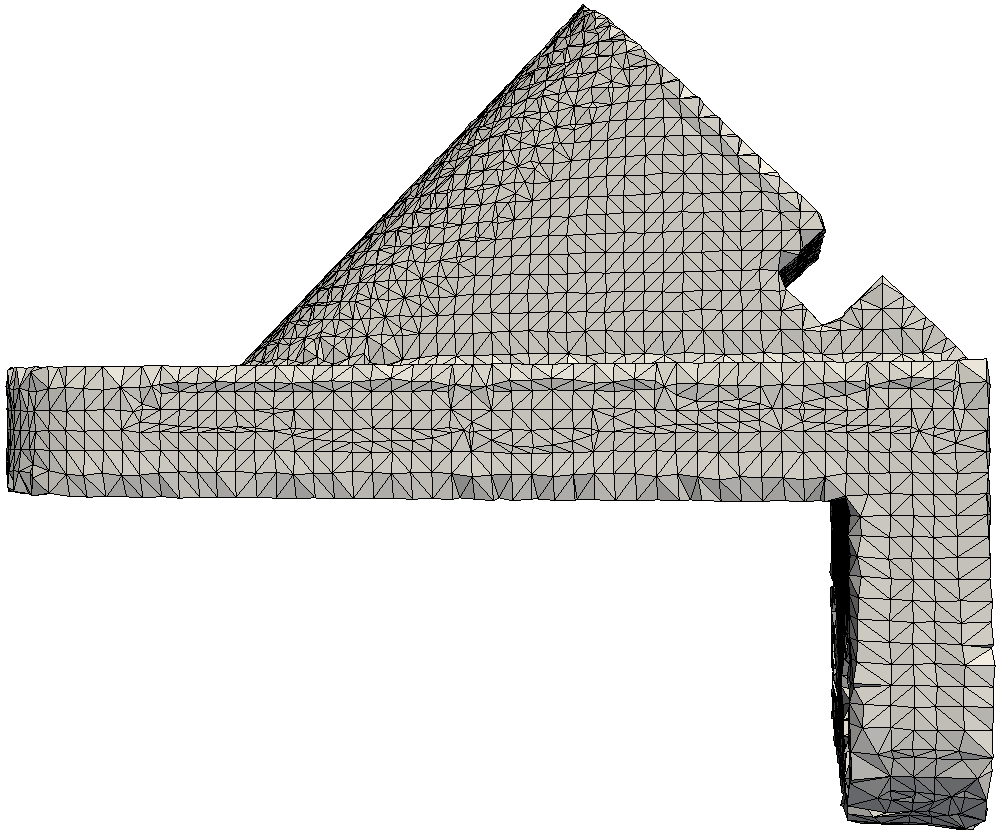
Bibtex
@article{ot_reconstruction,
year={2014},
issn={0924-9907},
journal={Journal of Mathematical Imaging and Vision},
volume={48},
number={2},
doi={10.1007/s10851-013-0414-y},
title={Feature-Preserving Surface Reconstruction and Simplification from Defect-Laden Point Sets},
url={http://dx.doi.org/10.1007/s10851-013-0414-y},
publisher={Springer US},
keywords={Optimal transportation; Wasserstein distance; Linear programming; Surface reconstruction; Shape simplification; Feature recovery},
author={Digne, Julie and Cohen-Steiner, David and Alliez, Pierre and de Goes, Fernando and Desbrun, Mathieu},
pages={369-382},
language={English}
}
year={2014},
issn={0924-9907},
journal={Journal of Mathematical Imaging and Vision},
volume={48},
number={2},
doi={10.1007/s10851-013-0414-y},
title={Feature-Preserving Surface Reconstruction and Simplification from Defect-Laden Point Sets},
url={http://dx.doi.org/10.1007/s10851-013-0414-y},
publisher={Springer US},
keywords={Optimal transportation; Wasserstein distance; Linear programming; Surface reconstruction; Shape simplification; Feature recovery},
author={Digne, Julie and Cohen-Steiner, David and Alliez, Pierre and de Goes, Fernando and Desbrun, Mathieu},
pages={369-382},
language={English}
}