Enchaînements d'instructions¶
Dans ce chapitre, nous abordons l'écriture d'un algorithme à proprement parler. Un algorithme est composé d'une série d'instructions, qui peuvent être enchaînées ou regroupées de différentes manières.
Séquence¶
La forme la plus simple d'enchaînement d'instructions composant une fonction est la séquence. Les instructions sont écrites l'une après l'autre, séparées par un saut de ligne. Pour Python, il est indispensable qu'elles soient toutes au même niveau d'indentation, c'est-à-dire précédées du même nombre d'espaces1. Les instructions d'une séquence sont toutes exécutées, dans l'ordre ou elles sont écrites.
Considérons par exemple l'algorithme suivant, calculant les trois premières puissances d'un nombre :
"""
:entrée x: float, SAISI au clavier
:pré-cond: Ø
:sortie p2: float, AFFICHÉ à l'écran
:sortie p3: float, AFFICHÉ à l'écran
:sortie p4: float, AFFICHÉ à l'écran
:post-cond: p2 = x², p3 = x³, p4 = x⁴
"""
x = float(input("x="))
p2 = x*x
p3 = p2*x
p4 = p3*x
print(p2, p3, p4)
On peut représenter l'enchaînement des instructions de cet algorithme par le diagramme ci-dessous :
![digraph sequence {
rankdir=LR; splines=line
node [ shape=box ]
i0 [ label="x = float(...)" ]
i1 [ label="p2 = x*x" ]
i2 [ label="p3 = p2*x" ]
i3 [ label="p4 = p3*x" ]
i4 [ label="print(p2, p3, p4)"]
i0 -> i1 -> i2 -> i3 -> i4
}](../_images/graphviz-73e9d238eabb7d06048d6277a19c472834e8d4ac.png)
Note
La spécification ne fait pas partie de l'algorithme (elle décrit le « quoi », pas le « comment »).
On l'encadre par des triples guillemets (""")
pour indiquer à Python qu'il peut ignorer cette partie lorsqu'il exécute l'agorithme.
Condition¶
Dans certains cas, il est nécessaire d'exécuter des instructions différentes selon qu'une condition est remplie ou non. Dans ce cas, on utilisera un enchaînement conditionnel. Celui-ci est composé ainsi :
première ligne :
le mot-clé
if,l'expression booléenne représentant la condition,
le caractère
:.
enchaînement d'insructions à exécuter si la condition est vraie
toutes avec un niveau d'indentation supérieur à la première ligne.
le mot-clé
else:au même niveau d'indentation que la première ligne.
enchaînement d'instructions à exécuter si la condition est fausse
toutes avec un niveau d'indentation supérieur à la première ligne.
NB : la clause else et les points suivants sont facultatifs.
Les enchaînements suivant le if et le else ne sont bien sûr
pas limités à des enchaînements séquentiels.
Il peuvent comporter d'autres enchaînements conditionnels,
ou des enchaînements répétitifs (cf. ci-dessous).
La première instruction
précédée du même nombre d'espaces (ou moins) que la première ligne (la ligne du if)
sera reconnue comme ne faisant pas partie de l'enchaînement conditionnel.
Elle sera donc exécutée que la condition soit vraie ou non.
Considérons par exemple l'algorithme suivant, qui calcule pour un nombre donné sa valeur absolue et son signe (représenté par le nombre 1 ou -1) :
"""
:entrée x: float, AFFECTÉ précédemment
:pré-cond: Ø
:sortie signe: int, AFFICHÉ à l'écran
:sortie valabs: float, AFFICHÉ à l'écran
:post-cond: signe = +1 si x ≥ 0, -1 sinon
:post-cond: valabs = |x|
"""
if x >= 0:
signe = +1
valabs = x
else:
signe = -1
valabs = -x
print(signe, valabs)
On peut représenter l'enchaînement des instructions de cet algorithme par le diagramme ci-dessous :
![digraph condition {
rankdir=LR; splines=line
node [ shape=box ]
t1 [ label="x >= 0", shape=diamond ]
i1 [ label="signe = +1" ]
i2 [ label="valabs = x" ]
i3 [ label="signe = -1" ]
i4 [ label="valabs = -x" ]
j1 [ label="", shape=none, width=0, height=0 ]
i5 [ label="print(signe, valabs)" ]
t1 -> i1 [ taillabel=" oui" ]
i1 -> i2; i2 -> j1 [ arrowhead=none ]
t1 -> i3 [ taillabel=" non" ]
i3 -> i4; i4 -> j1 [ arrowhead=none ]
j1 -> i5
}](../_images/graphviz-ba398d66546aea6e5544eab35ca546bf96482f13.png)
Conditions multiples¶
Afin d'éviter d'imbriquer les if et les else les uns
dans les autres, Python propose l'instruction elif (contraction
de else if) qui se traduit en langage courant par "sinon si".
Le elif doit être utilisé avec précaution et parcimonie,
uniquement lorsque l'on est certain que toutes les conditions
sont exclusives. En effet, les conditions sont vérifiées les unes
après les autres jusqu'à ce qu'une condition soit vraie. Si une
condition est vérifiée, les suivantes dans la liste ne sont pas
examinées.
Une suite de elif peut se terminer par un else qui sera
donc traité si aucune condition n'a été vérifiée jusque là.
Voici un exemple d'utilisation du elif,
qui donne le nombre de jours dans le mois donné (pour une année non bissextile) :
"""
:entrée mois: int, AFFECTÉ précédemment
:pré-cond: 1 ≤ mois ≤ 12
:sortie nbj: int, AFFECTÉ pour la suite
:post-cond: nbj est le nombre de jours du mois dont le numéro est donné
"""
if mois == 2:
nbj = 28
elif mois == 4 or mois == 6 or mois == 9 or mois == 11:
nbj = 30
else:
nbj = 31
Cette écriture est totalement équivalente à :
if mois == 2:
nbj = 28
else:
if mois == 4 or mois == 6 or mois == 9 or mois == 11:
nbj = 30
else:
nbj = 31
Répétition¶
Python supporte deux types d'enchaînements répétitifs,
également appelés « enchaînements itératifs » ou « boucles » :
la boucle while et la boucle for.
La boucle while¶
Dans certains cas,
il est nécessaire d'exécuter les mêmes instructions un nombre de fois variable
selon les valeurs d'entrée de l'algorithme.
Plus précisément, on répétera ces instructions
tant qu'une condition est remplie.
Dans ce cas, on utilisera une boucle while, qui est composée ainsi :
première ligne :
le mot-clé
while,l'expression booléenne représentant la condition,
le caractère
:.
enchaînement d'instructions à répéter tant que la condition est vraie
toutes avec un niveau d'indentation supérieur à la première ligne.
Ici encore, l'enchaînement d'instructions suivant le while peut comporter
tous types d'enchaînements (séquentiel, conditionnel, répétitif).
La première instruction
précédée du même nombre d'espaces (ou moins) que la première ligne (la ligne du while)
sera reconnue comme ne faisant pas partie de la boucle.
Elle sera donc exécutée dès que la condition devient fausse.
Considérons par exemple l'algorithme suivant qui calcule le nombre de chiffres (en base 10) nécessaires à l'écriture d'un entier positif :
"""
:entrée n: int, AFFECTÉ précédemment
:pré-cond: n > 0
:sortie c: int, AFFICHÉ à l'écran
:post-cond: n s'écrit en base 10 avec c chiffres
"""
c = 1
while n > 10:
c = c+1
n = n//10
print(c)
On peut représenter l'enchaînement des instructions de cet algorithme par le diagramme ci-dessous :
![digraph boucle_while {
rankdir=LR; splines=ortho
node [ shape=box ]
i1 [ label="c = 1" ]
t1 [ label="n > 10", shape=diamond ]
i2 [ label="c = c+1" ]
i3 [ label="n = n//10" ]
i4 [ label="print(c)" ]
i1 -> t1
t1 -> i2 [ taillabel="oui" ]
i2 -> i3
i3 -> i4 [ style=invis ]
i3:se -> t1:s [ constraint=false ]
t1:n -> i4 [ taillabel="non "; constraint=false ]
}](../_images/graphviz-afb6e59175f18bbe9b172efb2d8593f302ae5c59.png)
Il est intéressant de remarquer que, selon les valeurs en entrée, les instructions de la boucle peuvent être exécutée plusieurs fois, une seule fois, voire pas du tout (si n=7, par exemple, dans l'algorithme ci-dessus).
La boucle for¶
Certaines valeurs manipulées par un algorithme peuvent être vues comme « contenant » d'autres valeurs ; par exemple, une chaîne de caractères peut être vue comme une liste d'éléments plus simples que sont chacun de ses caractères.
Ces valeurs complexes sont qualifiées d'itérables en Python,
c'est-à-dire que l'on peut itérer dessus.
Autrement dit, on peut parcourir leurs éléments un par un, dans l'ordre,
et appliquer le même ensemble d'actions sur chacun d'eux.
Ceci s'effectue avec la boucle for, qui est composée ainsi :
première ligne :
le mot-clé
for,un nom de variable
le mot-clé
in,l'itérable sur lequel on veut boucler
le caractère
:.
enchaînement d'instructions à exécuter pour chaque élément de l'itérable
toutes avec un niveau d'indentation supérieur à la première ligne.
La première instruction
précédée du même nombre d'espaces (ou moins) que la première ligne (la ligne du for)
sera reconnue comme ne faisant pas partie de la boucle.
La variable nommée après le for prendra successivement pour valeur
chacun des éléments de l'itérable;
et pour chacun d'entre eux, les instructions de la boucle seront exécutées.
Considérons par exemple l'algorithme suivant qui retourne la chaîne de caractères « miroir » de la chaîne passée en entrée :
"""
:entrée s: str, SAISI au clavier
:pré-cond: Ø
:sortie r: str, AFFICHÉ à l'écran
:post-cond: r est la chaîne miroir de s
"""
s = input("s=")
r = ""
for c in s:
r = c+r
print(r)
Par exemple, si l'utilisateur saisit la chaîne « épater », cet algorithme affichera « retapé ».
Boucles avec range¶
Il existe un cas particulier de boucle extrêmement fréquent :
une boucle itérant sur des entiers successifs.
Pour répondre à ce besoin, Python fournit la fonction range,
qui fournit un itérable contenant une séquence d'entier.
Plus précisément :
range(i)itère sur l'intervalle [0,i[range(i, j)itère sur l'intervalle [i,j[
Note
Notez à nouveau l'interprétation des bornes en Python. La borne inférieure est toujours inclue, la borne supérieure est toujours exclue.
Considérons par exemple l'algorithme suivant qui retourne la factorielle de l'entier n :
"""
:entrée n: int, AFFECTÉ précédemment
:pré-cond: n ≥ 0
:sortie f: int, AFFICHÉ au clavier
:post-cond: f = n! = 1×2×3×...×(n-1)×n
"""
f = 1
for i in range(2, n+1):
f = f*i
print(f)
Notons que ce type de boucle for2
peut également s'écrire sous forme d'une boucle while :
1 2 3 4 5 6 | f = 1
i = 1 # 2 = valeur initiale du range
while i < n+1: # n+1 = valeur finale du range
f = f*i
i = i+1
print(f)
|
Le choix de l'une ou l'autre des écitures est une question de goût.
La boucle for a l'avantage d'être plus concise,
alors que la boucle while est plus explicite (notamment sur le fait qu'on ne rentre pas dans la boucle pour i = n+1).
La boucle while est aussi plus générale :
on peut faire varier i de différentes manières (par exemple, en le multipliant par deux à chaque itération),
mais il est plus facile d'oublier l'initialisation de la variable (ligne 3 ci-dessus)
ou sa modification en fin d'itération (ligne 6 ci-dessus).
Fonction¶
Une fonction est un enchaînement d'instruction auquel on donne un nom pour pouvoir le réutiliser plus tard. Toute fonction résoud un problème précis, et est donc accompagnée de la spécification de ce problème. À titre d'exemple, voici comment on peut ré-écrire l'algorithme ci-dessus, qui calcule la factorielle de n'importe quel entier strictement positif :
def factorielle(n: int) -> int:
"""
:pré-cond: n > 0
:post-cond: retoune n! = 1×2×3×...×(n-1)×n
"""
f = 1
for i in range(2, n+1):
f = f*i
return f
On constate que
la première ligne est composée ainsi :
le mot-clé
def, qui annonce que nous définissons une nouvelle fonction,le nom de la fonction,
la liste des paramètres d'entrée, entre parenthèse et séparés par des virgules (le cas échéant),
chaque paramètre est décrit par son nom, suivi de deux points (
:), suivi de son type de données,
le type de la valeur de retour, précédé par
->,le caractère deux points (
:).
Toutes les lignes suivantes ont un niveau d'indentation supérieur à la première.
La première ligne est suivie par la spécification du problème, encadrée par des triples guillemets (
"""). En général, on peut ommettre les paramètres d'entrée et de sortie, puisque l'infomation est déjà présente dans la première ligne3.La dernière ligne de l'algorithme comporte le mot-clé
return, suivi de la valeur à donner au paramètre de sortie.
Lorsqu'une fonction possède plusieurs paramètres de sortie, leurs types (sur la première ligne) sont mis entre parenthèses et séparés par des virgules. Les valeurs retournées sont simplement séparées par des virgules :
def encadre_racine_carrée(x: float) -> (int, int):
"""
:pré-cond: x ≥ 0
:post-cond: inf ≤ √x < sup
:post-cond: sup-inf = 1
"""
inf = 0
sup = 0
# (...) séquence d'inscruction
return inf, sup
Appel de fonction¶
Une fois que l'on a défini une fonction, cette dernière fait alors partie des « capacités » de l'ordinateur.
Pour indiquer à l'ordinateur qu'il doit appeler (ou utiliser) une fonction, on écrira une affectation dont :
la partie gauche comportera autant de variables que la fonction comporte de paramètres de sorties ;
la partie droite est constituée du nom de la fonction, suivi par la liste des valeurs des paramètres d'entrée, entre parenthèses et séparées, le cas échéant, par des virgules.
Par exemple :
>>> bi, bs = encadre_racine_carrée(2.0)
>>> k = max(2*j, i-1) # max() retourne la plus grande des valeurs passées en entrée
Dans les exemples ci-dessus, on voit que les valeurs passées aux paramètres d'entrée peuvent être des expressions complexes. On constate aussi que les variables recevant les valeurs des paramètres de sortie ne sont pas tenues d'avoir le même nom que ces paramètres (s'ils sont nommés) ; c'est l'ordre des variables qui détermine leur correspondance avec les paramètres de sortie.
Enfin, notons que, dans le cas particulier des fonctions n'ayant qu'un seul paramètre de sortie, l'appel à la fonction peut être utilisé directement dans une expression. Par exemple, au lieu d'écrire :
>>> i = factorielle(5)
>>> j = i-1
on peut écrire directement :
>>> j = factorielle(5)-1
Types particuliers de fonction¶
On définit ici quelques notions qui sont parfois utiles pour distinguer certains types particuliers de fonctions.
- effet de bord
tout effet produit par une fonction en dehors des valeurs qu'elle retoure. Un exemple classique d'effet de bord est l'affichage d'information à l'écran. Dans le chapitre sur les tableaux, nous rencontrerons un autre type d'effet de bord, lié aux paramètres d'entrée-sortie.
- fonction pure
toute fonction n'ayant aucun effet de bord, et dont les valeurs de retour dépendent exclusivement des valeurs passées en entrée. Des exemples de fonctions pures sont les fonctions mathématiques telles que sinus ou factorielle.
- procédure
une fonction ne retournant rien. Elle ne comporte donc pas d'instruction return, ou alors le return n'est suivi d'aucune valeur. Par définition, une telle fonction doit avoir des effets de bord (sans quoi elle n'aurait aucun effet, et donc aucune utilité). Un exemple de procédure est la fonction print, dont le seul effet est d'afficher les valeurs qui lui sont passées en entrée.
Puisqu'une procédure ne retourne aucune valeur, son appel se limitera au nom de la procédure suivi de ses paramètres, sans affectation :
>>> print("bonjour le monde")
Notons qu'une fonction peut n'être ni une fonction pure, ni une procédure :
la fonction input (vue précédemment) retourne une valeur (ce n'est donc pas une procédure) mais elle a aussi des effets de bord en affichant un message à l'écran et en sollicitant une action de l'utilisateur (ce n'est donc pas une fonction pure).
La fonction randrange(start, stop) retourne un entier aléatoire compris entre start et stop. Puisqu'elle retourne une valeur, ce n'est pas une procédure. Mais cette valeur ne dépend pas uniquement des paramètres d'entrées : en appelant deux fois de suite randrange(1, 7), on peut obtenir deux résultats différents. Ce n'est donc pas non plus une fonction pure.
Variables d'une fonction¶
On a présenté au chapitre précédent la notion de variable. Il convient de décrire ici les différentes catégories de variables utilisées dans une fonction. Elles sont au nombre de trois :
les variables correspondant aux paramètres d'entrée ;
les variables correspondant aux paramètres de sortie ;
les variables intermédiaires.
Les variables correspondant aux paramètres d'entrée ont une particularité : elles ont déjà une valeur au début de la fonction (on verra dans la section Appel de fonction d'où vient cette valeur). Elles n'ont donc pas besoin d'être affectées, et on évitera en général de changer leur valeur5.
Les variables correspondant aux paramètres de sortie, quant à elles,
doivent absolument être affectées dans la fonction,
puisque c'est le rôle de cette dernière de déterminer leur valeur (rappelons que les paramètres de sortie décrivent
la solution au problème que l'on cherche à résoudre).
Ces valeurs sont transmises à l'appelant par l'instruction return
à la fin de la fonction.
Les variables intermédiaires, enfin, sont toutes les autres variables
qui peuvent être nécessaires au calcul des paramètres de sortie.
Par définition, elles n'ont pas de valeur initialement (elle doivent donc être affectées avant d'être utilisées),
et leur valeur est « oubliée » à la fin de la fonction (puisqu'elles ne sont pas données à l'instruction return).
Note
Même si c'est souvent préférable,
il n'est pas techniquement indispensable d'avoir une variable par paramètre de sortie.
L'instruction return peut être suivie d'une expression complexe,
impliquant des variables d'entrées et/ou des variables intermédiaires.
Exemple :
def prochain_multiple_de_7(n:int) -> int:
"""
:pré-cond: n ≥ 0
:post-cond: retourne le plus petit multiple de 7 supérieur à n
"""
return (n//7+1)*7
Si l'on voit la fonction comme une boîte noire dont le rôle est d'effectuer une opération précise, alors :
les paramètres d'entrée contiennent les valeurs passées à la boîte noire ;
les paramètres de sortie contiennent les valeurs retournées par la boîte noire ;
les variables intermédiaires sont invisibles en dehors de la boîte noire.
Imaginons que le rôle de notre boîte noire soit de déterminer quelles sont la plus petite et la plus grande valeur d'une liste de valeurs, ainsi que la moyenne des éléments de la liste. La liste de valeur est notre paramètre d'entrée, le minimum, le maximum et la moyenne sont les paramètres de sortie, et on imagine aisément que d'autres variables temporaires sont utilisées à l'intérieur de la fonction pour effectuer les calculs intermédiaires (par exemple, la somme des valeurs et le nombre de valeurs, nécessaires au calcul de la moyenne).
Portée des variables¶
Les variables utilisées dans une fonction sont propres à cette fonction. Elles ne sont ni visibles, ni utilisables depuis d'autres fonctions, même si ces dernière définissent une variable ayant le même nom. On dit que la portée de la variable est limitée à la fonction qui la définit6.
Considérons l'exemple ci-dessous :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | def nb_chiffres(n: int) -> int:
"""
:pré-cond: n > 0
:post-cond: retourne le nombre de chiffres nécessaires
pour écrire n en base 10
"""
c = 1
while n > 10:
c = c+1
n = n//10
return c
def total_chiffres_fact(n: int) -> int:
"""
:pré-cond: n > 0
:post-cond: retournr le nombre total de chiffres nécessaires pour
écrire les factorielles de tous les entiers entre 1 et n
"""
f = 1
c = 0
for i in range(1, n+1):
f = f*i
c = c+nb_chiffres(f)
return c
|
La fonction total_chiffres_fact appelle la fonction nb_chiffres.
On remarquera que ces deux fonctions utilisent les mêmes noms de variable (n, c).
Cependant, il n'y a aucune interaction entre
la valeur de n (respectivement de c) dans nb_chiffres et
la valeur de n (respectivement de c) dans total_chiffres_fact.
Il faut imaginer que,
lorsque l'ordinateur exécute total_chiffres_fact,
il stocke les valeurs de n, c et f dans un emplacement E1 de sa mémoire,
qui est dédié aux variables définies dans cette fonction.
Lorsqu'à la ligne 13, on lui demande d'exécuter la fonction nb_chiffres,
il laisse de coté l'emplacement E1 et
commence à travailler sur un emplacement E2,
dédié aux variables de nb_chiffres,
dans lequel il va stocker
les valeurs de n et c de nb_chiffres.
Lorsque cette dernière se termine, l'emplacement E2 est supprimé,
et l'ordinateur travaille à nouveau sur l'emplacement E1
pour terminer l'exécution de total_chiffres_fact,
ou n et c ont gardé les valeurs qu'elles avaient juste avant l'appel à nb_chiffres.
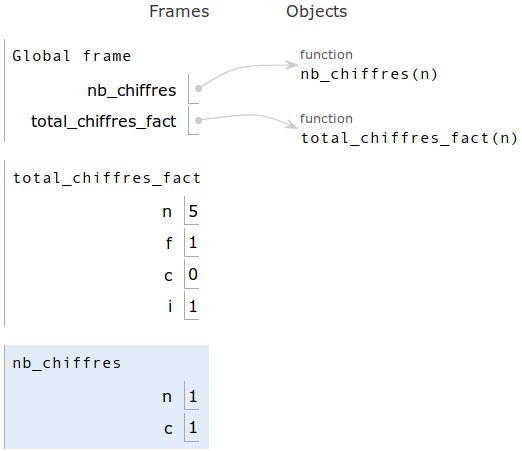
Fig. 1 Les variables de chaque fonction existent à des endroits différents de la mémoire, même lorsqu'elles ont le même nom.¶
Vous pouvez faire la simulation sur Pythontutor pour mieux comprendre comment sont gérés les espaces mémoires
Il est cependant important de détailler ce qui se passe aux moments du passage de E1 à E2, et du retour de E2 à E1 :
au moment de passer de la fonction appelante (E1) à la fonction appelée (E2), les expressions passées aux paramètres d'entrée (entre les parenthèses) sont calculées avec les variables de E1, et leurs valeurs sont affectées aux variables correspondantes dans E2 ;
au moment de revenir de la fonction appelée à la fonction appelante, les valeurs des paramètres de sortie sont affectées aux variables correspondantes dans E1, ou substituées à l'appel de fonction si celui-ci est utilisé directement dans une expression7.
Considérons l'exemple ci-dessus,
où on aurait appelé la fonction total_chiffres_fact avec n=5.
Au premier passage à la ligne 13,
les variables de total_chiffres_fact ont les valeurs suivantes :
n=5, c=0, i=1 et f=1.
À ce moment, l'ordinateur calcule
les valeurs à passer aux paramètres d'entrée de nb_chiffres,
en l'occurrence un seul paramètre, dont la valeur est 1 (valeur de f).
L'emplacement mémoire qui contiendra les variables de nb_chiffres
est donc initialisé avec n=1.
À la fin de l'exécution de nb_chiffres, ses variables ont pour valeur
n=1 et c=1 (cf figure 1).
Comme nb_chiffres est utilisée directement dans une expression,
la valeur du paramètre de sortie c est substituée à l'appel de fonction,
donc la ligne 13 de total_chiffres_fact revient ici à calculer :
c = c+1
dans l'emplacement mémoire de total_chiffres_fact, donc avec c=0.
Notons aussi que la valeur de n dans total_chiffres_fact est toujours 5,
et n'a pas été influencée par le fait que nb_chiffres utilisait
une variable du même nom avec une valeur différente.
L'apparente complexité de ce processus est en fait une simplification : elle permet au programmeur d'une fonction f de ne pas se soucier des noms de variables utilisés dans les autres fonctions (celles appelées par f comme celles qui appellent f). Il favorise donc la modularité du code.
Notes de bas de page
- 1
Dans la plupart des autres langages de programmation, l'indentation n'est pas obligatoire. Cependant, elle est un aspect important de l'écriture d'algorithmes. Une indentation claire et cohérente facilite grandement la lecture et la compréhension. Vous devriez donc toujours la considérer comme un obligation, même dans des langages qui ne l'imposent pas.
Lorsqu'on écrit des algorithmes à la main sur papier, il peut être utile de matérialiser les niveaux d'indentation par des lignes verticales.
- 2
En fait, n'importe quelle boucle
forpeut s'écrire sous forme d'une bouclewhile.- 3
En fait, la première ligne n'indique que les paramètres d'entrée « PASSÉS en paramètres », et les paramètres de sortie « RETOURNÉ ». Si la fonction attend d'autres entrées (par exemple saisies au clavier) ou fournit d'autres sorties (par exemple affichées à l'écran), il conviendra de déclarer ces paramètres supplémentaire explicitement.
- 4
On dit d'ailleurs couramment qu'une fonction retourne ses paramètres de sortie.
- 5
Ceci n'est en rien une contrainte technique, mais plutôt une règle de bonne pratique (cf. Bonnes pratiques de programmation). Et même cette règle peut, dans certains cas, souffrir des exceptions.
- 6
Il est possible, en Python et dans d'autres langages, de définir des variables avec une portée plus petite ou plus grande, mais nous ne traiterons pas de cela dans ce cours.
- 7
En fait, c'est l'expression passée à
returnqui est systématiquement substituée à l'appel de la fonction. Python autorise une utilisation beaucoup plus souple de l'instructionreturnque celle préconisée dans ce cours.