Equivalences en jeux
Table of Contents
1 Contexte
Nous considérons des jeux à deux joueurs, impartiaux (i.e., mêmes règles du jeu pour les deux joueurs), à information complète (i.e., chaque joueur connait tout de l'état du jeu), progressivement bornés (i.e., pour toute position \(x\), le jeu se terminera après un nombre fini \(B(x)\) de coups, et en forme normale (i.e., le premier joueur à ne plus pouvoir jouer a perdu).
Nous dirons position gagnante (G) pour une position à partir de laquelle un joueur parfait est sûr de gagner. C'est-à-dire qu'il possède une stratégie gagnante i.e., un algorithme qui place le jeu en position perdante pour son adversaire.
Nous dirons position perdante (P) pour une position à partir de laquelle un joueur, quel qu'il soit, ne gagnera jamais face à un joueur parfait. Autrement dit, quelque soit le coup qu'il choisit, le jeu passe en position gagnante pour son adversaire.
2 Un premier jeu
Soit une pile d'objets. Un coup consiste à retirer \(1\) ou \(2\) objets de la pile. Soit \(m\) le nombre d'objets de la pile.
- Qu'est-ce qu'une position perdante ?
- \(m \; mod \; 3 = 0\)
- Qu'est ce qu'une position gagnante ?
- \(m \; mod \; 3 \neq 0\)
- Qu'est ce qu'une stratégie gagnante ?
- Retirer \(m \; mod \; 3\) objets.
3 Représentation sous forme de graphe
Nous pouvons représenter un jeu comme un graphe dont les nœuds sont des positions et les arêtes sont des coups. Alors, une position perdante est un nœud dont toutes les arêtes sortantes pointent vers une position gagnante. De même, une position gagnante est un nœud pour lequel au moins une arête sortante pointe vers une position perdante. Sur l'exemple précédent, cela donne :
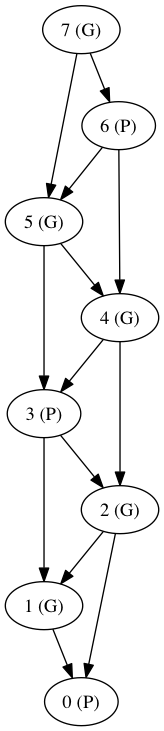
4 Jeux à soustractions
Un jeu à soustractions est formé d'une pile d'objets et d'un ensemble \(S\) d'entiers. A chaque coup, le nombre d'objets retirés de la pile doit être un élément de \(S\).
Par exemple, avec \(S = \{1 \; , \; 2 \; , \; 3 \; , \; 4\}\) :
| Pos | G/P | coup |
|---|---|---|
| 0 | P | |
| 1 | G | 1 |
| 2 | P | |
| 3 | G | 3 |
| 4 | G | 4 |
| 5 | G | 3 |
| 6 | G | 4 |
| 7 | P | |
| 8 | G | 1 |
| 9 | P | |
| 10 | G | 3 |
| 11 | G | 4 |
| 12 | G | 3 |
| 13 | G | 4 |
Nous remarquons une schéma de période 7. En fait, une telle périodicité dans la structure G/P existe toujours pour un jeu à soustractions. Prouvons-le.
Soit \(S\) un ensemble fini de soustractions.
Soit \(M\) son plus grand élément.
Depuis chaque position, il y a au plus \(M\) coups possibles.
Soit \(k\) une position.
Soit \(W.k\) un prédicat vrai ssi la position \(k\) est gagnante.
Pour \(k \geq M\), la valeur booléenne \(W.k\) est déterminée par la suite \((W.(k-1), W.(k-2),\dots,W.(k-M)\) notée \(s.k\).
Il y a \(2^M\) suites distinctes formées de \(M\) valeurs booléennes.
Ainsi, la suite \((s.(M+1), s.(M+2),\dots)\) doit se répéter après au plus \(2^M\) étapes.
Autrement dit, il existe un entier \(R\), avec \(M \leq R \leq M+2^M\) tel que \(s.M = s.R\).
Donc, \(W.M = W.R\), et la suite \(W\) se répète à partir du rang \(R\).
Q.E.D.
Par exemple, avec \(S = \{1 \; , \; 3 \; , \; 4\}\), \(W\) doit se répéter à partir d'un rang au plus égal à \(20 = 4 + 2^4\), et en fait à partir du rang \(7\). Autrement dit, pour une position \(k\) quelconque, \(W.k = W.(k \; mod \; 7)\).