Recuit Simulé
Table of Contents
1 Recherche locale itérative et recuit simulé
1.1 Hill-Climbing
L'approche itérative la plus naïve pour la résolution d'un problème combinatoire est le "hill-climbing" (ou "gradient-descent"). Il s'agit de générer une solution initiale puis, tant que possible, se déplacer vers une solution voisine meilleure.

Figure 1: Algorithme Hill-Climbing pour la recherche locale
Le problème principal de cette approche est qu'un optimum local peut être très éloigné de l'optimum global.
1.2 Recuit simulé
Le recuit simulé ("simulated annealing") est un algorithme itératif qui apporte une solution au problème de l'attraction par les optimums locaux. Une solution voisine meilleure que la solution actuelle sera toujours acceptée. Une solution voisine moins bonne que la solution actuelle sera parfois acceptée selon la probabilité :
\begin{equation*} e^{\frac{f(u)-f(v)}{kT}} \end{equation*}En thermodynamique, la probabilité de trouver une système dans un état d'énergie \(E\) à une température \(T\) est proportionnelle à \(e^{-\frac{E}{kT}}\) où \(k\) est la constante de Boltzmann (\(1.3896 \times 10^{-23}\) joule/kelvin). Le facteur de Boltzmann est le rapport entre deux états d'énergies \(E1\) et \(E2\): \(e^{-\frac{\Delta E}{kT}}\).
Par exemple, une molécule de gaz dans l'atmosphère terrestre a son plus bas niveau d'énergie au niveau de la mer. Son énergie augmente avec l'altitude. La probabilité de trouver la molécule 10 mètres au dessus du niveau de la mer est presque identique à celle de la trouver au niveau de la mer car \(\Delta E\) est très petit par rapport à \(kT\). Le ratio des probabilités de ces deux niveaux d'énergie est proche de 1. Mais quand l'altitude augmente, la différence des probabilités des niveaux d'énergie augmente. La probabilité de trouver la molécule à une haute altitude décroit exponentiellement avec l'augmentation linéaire de l'altitude. Par contre, si la température augmente, la probabilité de trouver une molécule à une haute altitude augmente également.
Ainsi, le recuit simulé débute avec une température élevée qui permet d'explorer de nombreuses solutions en s'échappant des minimums locaux. Un refroidissement progressif permet d'approcher une bonne solution de faible énergie.
Ci-dessous des graphes de cette distribution pour différentes valeurs de \(T\) (avec GNU Octave).
x = -2:0.1:0;
y1 = exp(x/0.5);
y2 = exp(x/0.3);
y3 = exp(x/0.1);
plot(x,y1,x,y2,x,y3);
xlabel('f(u)-f(v)');
ylabel('exp((f(u)-f(v))/T)');
legend('T=0.5','T=0.3','T=0.1');
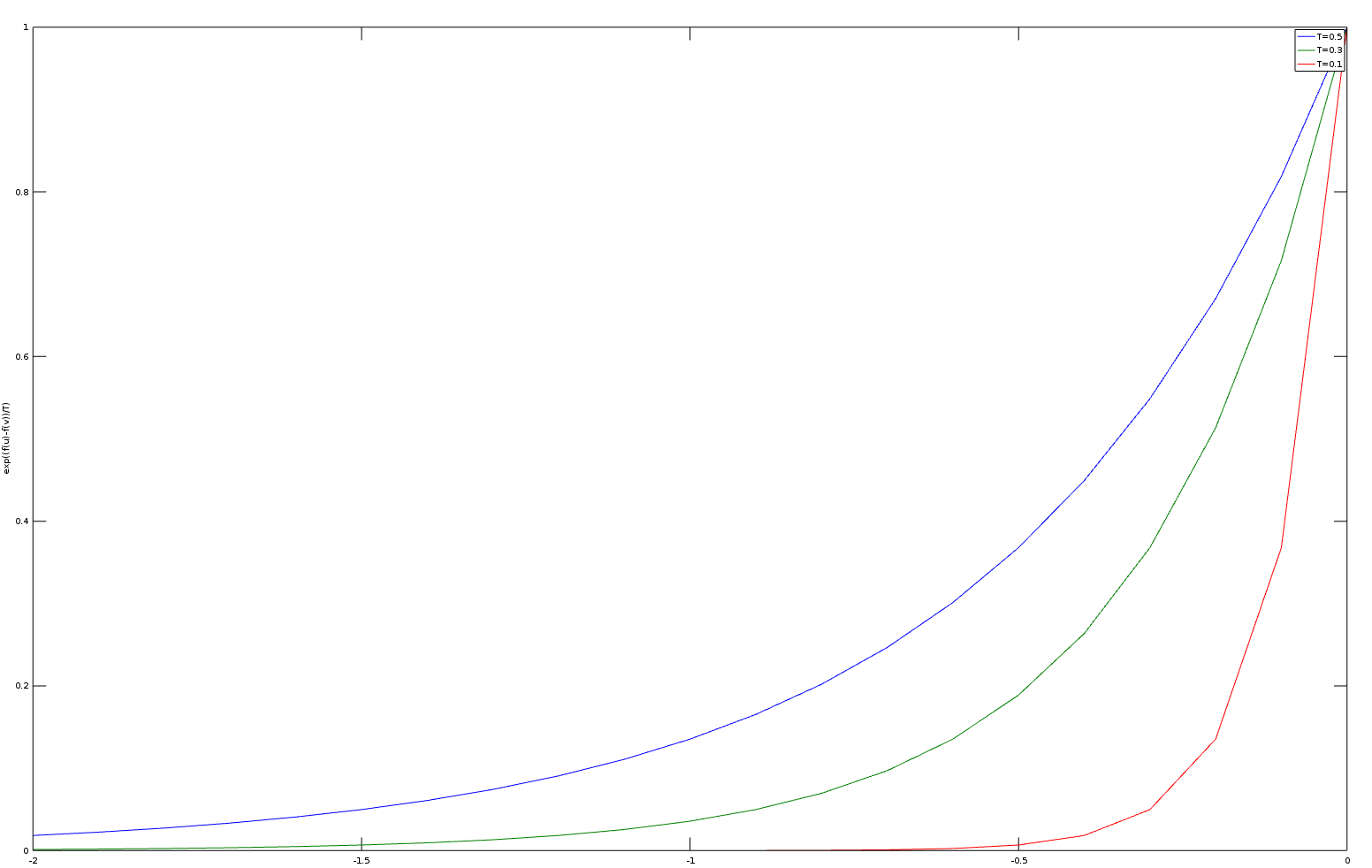

Figure 3: Algorithme Simulated Annealing
2 Implémentation
2.1 Générateur de nombre aléatoire
Nous commençons par introduire un générateur de nombres aléatoires classique qui sera utilisé pour l'implémentation de l'algorithme itératif du recuit simulé. Nous avons besoin d'un générateur qui respecte une distribution uniforme. Il s'agit par exemple de générer aléatoirement un nombre à virgule flottante sur l'intervalle \([0.0 .. 1.0]\) et chaque nombre doit être équiprobable.
Commençons par quelques remarques générales :
- Nous aurons besoin de l'implémentation d'opérations arithmétiques sur des valeurs codées avec 64 bits et non signées.
- Une notion clé sera la période du générateur qui ne devrait pas être inférieure à \(\text{~} 2^{64}\).
- Il ne faudra pas utiliser les implémentations par défaut des langages C, C++, Matlab, etc. (e.g.,
rand,srand, etc.) car leur implémentation n'étant pas standardisée, elles ne sont pas toujours d'une qualité suffisante (nous allons comprendre pourquoi…).
2.1.1 Approche par congruence linéaire
Les premiers générateurs conçus dans les années 1950 sont fondés sur un principe de congruence linéaire (LCG : linear congruential generator). Il s'agit d'utiliser une équation de récurrence linéaire :
\begin{equation*} I_{j+1} = aI_j + c \; (mod \; m) \end{equation*}Sont particulièrement intéressants les triplets \((a,c,m)\) tels que la période de la récurrence atteigne \(m\).
Malheureusement, il y a des corrélations entre sous-séquences de la récurrence. Par exemple, si \(k\) générateurs sont utilisés pour générer des points dans un espace à \(k\) dimensions, ces points vont se répartir sur des (k-1)-hyperplans parallèles entre eux (au plus \(m^{1/k}\) plans).
Ainsi, la méthode du test spectral a été introduite pour mesurer la qualité d'un générateur LCG (pour aller plus loin que ce rapide survol, voir la section 3.3.4 de "The Art of Computer Programming" de Donald Knuth).
Soit \(< I_n >\) la séquence de période \(m\) associée au générateur (i.e., on suppose que le triplet \((a,c,m)\) a été choisi de telle sorte que la période du générateur soit effectivement \(m\) ). On considère l'ensemble des \(m\) points :
\begin{equation*} \{ \frac{1}{m} (I_n,\dots,I_{n+t-1}) \; | \; 0 \leq n < m \} \end{equation*}d'un espace à \(t\) dimensions. En posant : \(s(x) = ax + c \; (mod \; m)\), cet ensemble s'écrit :
\begin{equation*} \{ \frac{1}{m} (x, s(x), \dots,s^{t-1}(x)) \; | \; 0 \leq x < m \} \end{equation*}Le graphe de cet ensemble de points montre des régularités : les \(t\)-uplets de nombres aléatoires vivent sur des hyperplans parallèles de dimensions \(t-1\).
Par exemple, en dimension 2 on notera \(1/\nu_2\) la distance maximale entre deux lignes parallèles ; le maximum étant pris sur l'ensemble des familles de lignes parallèles qui couvrent chacune les points \((x/m, s(x)/m)\).
\(\nu_t\) est appelée la précision du générateur aléatoire.
Pour fixer les idées, il semble assez juste de dire qu'une suite de \(t\) nombres générés aléatoirement correspond à une suite de \(t\) nombre "vraiment" aléatoires mais tronqués aux plus proches multiples de \(1/\nu_t\) (ou, de manière équivalente, dont la représentation est tronquée à \(log(\nu_t)\) bits). Il faut bien noter que la précision \(\nu_t\) diminue avec l'augmentation de \(t\) (c'est assez intuitif car la période \(m\), et donc le nombre de points, reste constante).
Pour se rendre compte du problème et voir des graphes de tests spectraux pour des générateurs traditionnels, se référer au travail de Entacher : "A collection of selected pseudorandom number generators with linear structures". En fait, beaucoup de générateurs très utilisés ne sont pas satisfaisants (voir par exemple le cas de Matlab).
2.1.2 Approche par équivalence booléenne
Nous introduisons une autre technique fondée sur l'équivalence booléenne (en fait sa négation notée \(\not\equiv\) ou \(\oplus\), i.e. le XOR). Puis nous proposerons une combinaison de ces deux techniques afin de fournir un générateur de nombres aléatoires de qualité.
Une technique très simple consiste à faire trois shift et trois xor pour calculer le prochain nombre aléatoire :
Afin de comprendre le principe de cette approche, considérons \(x\) comme un vecteur de \(\mathbb{Z}/2\mathbb{Z}^{64}\) (i.e., un vecteur de dimension 64 dont chaque composante est une valeur booléenne). Nous nous plaçons ainsi dans un espace vectoriel avec pour "addition" \(\oplus\) et pour "multiplication" \(\wedge\).
Prenons un exemple simple dans un espace à trois dimensions :
\begin{equation*} (011)_2 \oplus (\; (011)_2 >> (001)_2 \;) = (011)_2 \oplus (001)_2 = (010)_2 \end{equation*}Nous proposons une notation matricielle équivalente :
\begin{equation*} \begin{pmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 1 & 1 \end{pmatrix} \bullet \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \end{equation*}Ainsi, \(x \oplus (x >> a_1)\) équivaut au produit matriciel \(S_{a_1} \bullet x\). Avec, sur notre petit exemple à 3 dimensions, la matrice :
\begin{equation*} S_1 = \begin{pmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 1 & 1 \end{pmatrix} \end{equation*}Donc, le calcul du prochain nombre aléatoire correspond à la transformation linéaire : \(T = S_{a_3} S_{a_2} S_{a_1}\).
Il faut trouver des triplets \((a_1, a_2, a_3)\) tels que la période de la séquence aléatoire générée soit \(M = 2^{64} - 1\) (\(2^{64}\) est impossible car le \(0\) est absorbant). Il faut et il suffit que \(T^M = 1\) et \(T^N \neq 1\) pour tout \(N \in \{M/6700417 \; , \; M/65537 \; , \; M/641 \; , \; M/257 \; , \; M/17 \; , \; M/5 \; , \; M/3\}\) (i.e., \(M\) divisé par ses facteurs premiers).
2.1.3 Un générateur simple et fiable
Finalement, nous proposons un générateur qui a de bonnes propriétés et qui est simplement la combinaison des deux stratégies introduites plus haut (i.e., congruence linéaire et utilisation du XOR).
Nous utilisons un raccourci (Ullong) pour le type entier 64 bits, ce type fonctionnera avec la plupart des compilateurs (dont GNU g++) mais peut-être pas tous car ce type n'est pas dans le standard C++.
Le code du générateur aléatoire vient de l'ouvrage "Numerical Recipes, the Art of Scientific Computing" :
struct Ran { Ullong v; Ran(Ullong j) : v(4101842887655102017LL) { v ^= j; v = int64(); } inline Ullong int64() { v ^= v >> 21; v ^= v << 35; v ^= v >> 4; return v * 2685821657736338717LL; } inline double doub() { return 5.42101086242752217E-20 * int64(); } inline uint int32() { return (uint)int64(); } };