Interpolated corrected curvature measures for polygonal surfaces

Abstract

A consistent and yet practically accurate definition of curvature onto polyhedral meshes remains an open problem. We propose a new framework to define curvature measures, based on the Corrected Normal Current, which generalizes the normal cycle: it uncouples the positional information of the polyhedral mesh from its geometric normal vector field, and the user can freely choose the corrected normal vector field at vertices for curvature computations. A smooth surface is then built in the Grassmannian $\mathbb{R}^3\times\mathbb{S}^2$ by simply interpolating the given normal vector field. Curvature measures are then computed using the usual Lipschitz–Killing forms, and we provide closed-form formulas per triangle. We prove a stability result with respect to perturbations of positions and normals. Our approach provides a natural scale-space for all curvature estimations, where the scale is given by the radius of the measuring ball. We show on experiments how this method outperforms state-of-the-art methods on clean and noisy data, and even achieves pointwise convergence on difficult polyhedral meshes like digital surfaces. The framework is also well suited to curvature computations using normal map information.

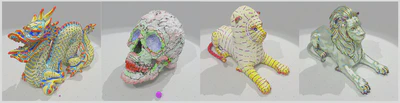
Caption: Left: mean curvature estimation. Middle left: convex, concave and saddle parts estimation on noisy data. Middle right: second principal curvature and direction estimation on coarse “Lion” mesh. Right: mean curvature extraction on the same “Lion” mesh geometry but with normal vector field given by normal map.

@article{lachaud2020,
      author = {Jacques-Olivier Lachaud and Pascal Romon and Boris Thibert and David Coeurjolly},
      journal = {Computer Graphics Forum (Proceedings of Symposium on Geometry Processing)},
      number = {5},
      title = {Interpolated corrected curvature measures for polygonal surfaces},
      volume = {39},
      month = jul,
      year = {2020}
}