Recherche de Courbes dans un Nuage de Points

Encadrants : Fabrice Jaillet (LIRIS-ORIGAMI)
Collaboration : (Universidad de Concepción, Chili)
Détails : Le stage se déroulera au sein du laboratoire LIRIS (bâtiment Nautibus).
Domaine : informatique graphique, algorithmie géométrique, IA
Compétences requises : C++

Sujet : le problème s’énonce simplement : trouver des courbes (comme sur l’image de gauche) passant exactement par certains points dans un nuage de points entiers 2D (à droite) !

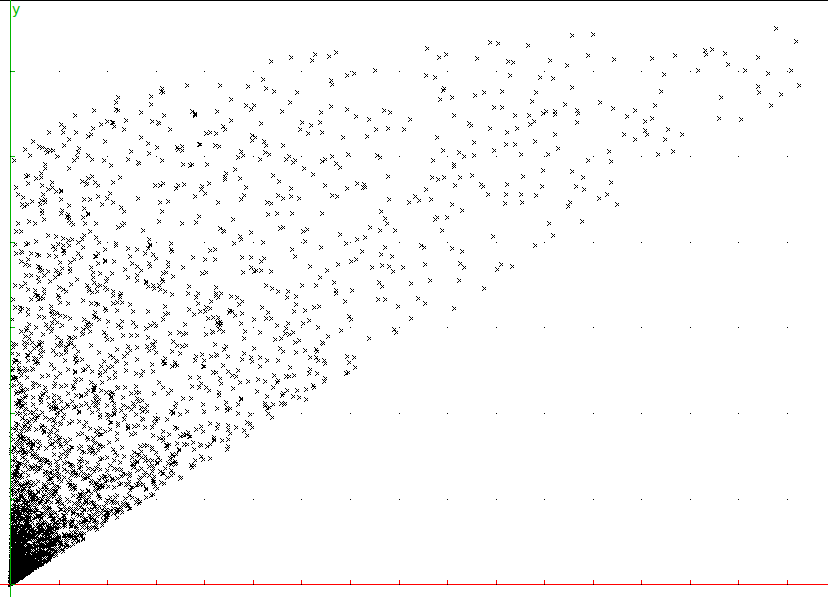
Le contexte : en théorie des nombres, il n’y a pas que le théorème de Fermat ! Le problème de Büchi (Büchi's Problem, Wikipedia), aussi connu comme les n-ièmes différences des carrés, reste encore ouvert ! Les séries de Büchi sont des séquences d’entiers telles que la seconde différence de leurs carrés est constante et égale à 2.

Par exemple, si x₁=1, x₂=2 et x₃=3, alors (x₃)²-(x₂)²=9-4=5 et (x₂)²-(x₁)²=4-1=3, et 5-3=2 ! Cela marche pour toute série d’entiers dont les valeurs absolues sont consécutives, et ces séries sont appelées triviales, par exemple [-7,6,5,4,-3,-2,1,0,-1,2]. Celles dont les valeurs sont non consécutives sont plus intéressantes, par exemple [6,23,32,39]. Il existe une infinité de suites (non-triviales) de longueur 3 et 4. Celles de longueur 3 sont parfaitement connues. Celle de longueur 4 ne sont que partiellement décrites, grâce notamment aux chercheurs de l’Universidad de Concepción, au Chili. Par contre, il n’existe pas de suite connue de longueur 5….

La question posée est donc de savoir s'il existe une limite M, telle qu’il n’existe plus de série non triviale de longueur M. Répondre à cette question permettrait de résoudre un certain nombre d’autres problèmes en théorie des nombres et en logique mathématique, dont savoir si un système particulier d’équations a une solution ou non.

Dans ce projet, une des pistes de recherche concerne le paramétrage polynomial de ces suites de Büchi de longueur 4. On sait que certains points sont liés par une courbe paramétrée polynomiale. Si les premières courbes de degré peu élevés ont été trouvées « à l’oeil », celles de degré plus élevé (6 et plus) ne sont pas évidentes. Et trouver un maximum de courbes permettrait de trouver des relations entre elles et d’être capable de générer un maximum de séquences facilement. Une des difficultés ici est de manipuler ces suites, dont les valeurs sont rapidement très grandes (même si leur paramétrage dans le plan est plus simple) :

Exemples de suites : ([127261567962,816475242713,1147635890536,1402677601065],
ou [91075841944817097,91076096988493904,91076352031456505,91076607073704906]).

L’objectif du projet est donc :

• Génération d’un très grand nombre de suites de Büchi de longueur 4, et les afficher dans le plan. Test si une d'elles engendre une suite de longueur 5 !

• Proposition d’une méthode de recherche de courbes polynomiales passant par certains points ! Attention, on travaille sur des entiers, donc les techniques classiques d’approximation ne fonctionnent pas…. On pourra regarder des méthodes de type k-means, RANSAC, ou machine-learning

• Implémentation d’un de ces algorithmes.

• Extension possible : en utilisation les propriétés géométriques, on peut « plonger » les points 2D dans un espace 3D ou plus, le problème revient alors à chercher des droites dans ce nouvel espace, plutôt que des courbes en 2D, à priori plus simple...