Cette page explique :

Comment lancer l'application ?

Repertoire ou se trouvent les donnees : gkit2light/data/

gkit2light/data/ textures : pour placer des textures
gkit2light/data/ CreateMesh : programme pour creer des maillages de tissu ou convertir des fichiers .obj .off en fichiers pour l'application
gkit2light/data/ drap10 : fichiers de donnees d'un tissu de 10 * 10 particules
gkit2light/data/ drap70 : fichiers de donnees d'un tissu de 70 * 70 particules
gkit2light/data/ vache : fichiers de donnees d'une vache
gkit2light/data/ sphere : fichiers de donnees d'une sphere
gkit2light/data/ bunny : fichiers de donnees du Standford bunny

Plusieurs fichiers dans ces repertoires

faceset.eti : definition des facettes triangulaires de l'objet
masses.eti : definition des masses associees aux sommets de l'objet
points.eti : definition des coordonnees (x,y,z) des sommets de l'objet
texcoord.eti : definition des coordonnees de textures des sommets de l'objet

Repertoire pour l'execution de l'application : gkit2light/src/master_MecaSim/exec/

Fichier_Param.simu : parametres de la simulation - gravite, viscosite, nb iterations
Fichier_Param.objet : parametres de l'objet simule - donnees, k, nu, dt, etc.

Pour lancer l'application depuis le repertoire gkit2light

Creer un fichier qui s'appelle go
Mettre dedans l'instruction suivante : ./bin/master_meca_sim_etudiant 1 ./src/master_MecaSim/exec/Fichier_Param.simu ./src/master_MecaSim/exec/Fichier_Param.objet1
Faire : chmod +x go
Lancer : ./go depuis le repertoire gkit2light
ou de maniere generale : Executable nbObjet fichier_param_simulation fichier_param_Obj1 fichier_param_Obj2 ...

Viewer de l'application

La methode init() de Viewer (dans Vierwer-init.cpp) permet de creer le maillage des objets servant pour leur affichage.

La methode render() de Viewer permet l'affichage les maillages (de type Mesh) des objets de la scene. Pour cela nous invoquons gl.draw() sur les Mesh des elements de la Scene. La classe Noeud comporte ainsi le membre m_ObjetSimule de type Mesh (maillage servant a l'affichage des objets simules).

La methode update() de Viewer permet de mettre a jour le Mesh des objets (maillage de l objet cree pour effectuer l affichage) en invoquant la methode updateVertex() pour chacun des elements du graphe de scene. La methode Simulation est notamment invoquee dans cette methode.

La touche 'h' permet de faire apparaitre le menu d'aide de l'application : affichage plein ecran, zoom, etc.

Le graphe de scene

Le graphe de scene est defini dans la classe Viewer par la variable _Simu de type Scene. Il permet de gerer les differents objets de la scene (qui sont attaches a la scene des leur creation).

La classe Scene contient ainsi la liste des Noeud de la scene (les enfants). Chaque objet que nous souhaitons gerer doit ainsi heriter de la classe Noeud. Par exemple la classe ObjetSimule herite de la classe Noeud.
Les differentes methodes de la classe Scene vont permettre d'appeler les methodes correspondantes pour chacun des objets Noeud attaches a la scene. Les methodes virtuelles pures de la classe Noeud doivent ainsi obligatoirement etre implementees dans les classes relatives aux differents objets de la scene (meme si elles ne font rien).
- La methode initObjetSimule() de Scene permet d'initialiser les structures de donnees des objets a partir des donnees fournies par les fichiers de donnees (definition des positions des particules, des masses, etc.)
- La methode initMeshObjet() de Scene permet d'initaliser le maillage (de type Mesh) de l'objet pour effectuer son affichage par le viewer.
- La methode Simulation() de la classe Scene permet d'effectuer les differents calculs d'un pas de temps de simulation pour l'ensemble des elements attaches a la Scene.
A noter que, la gravite et la viscosite du milieu sont definies dans la Scene, c'est-a-dire que leurs proprietes sont identiques pour chacun des objets simules. Leurs caracteristiques sont fournies au lancement de l'application via le fichier de donnees.

Representation d'un objet de la scene pour le visualiser

Les principales structures de donnees relatives a un objet pour effectuer sont affichages sont les suivantes :

La structure _VIndices contient les indices des sommets du maillage decrivant l'objet visualise. Sa taille est definie par _VISize qui vaut trois fois le nombre de facettes puisqu'une facette est definie par trois sommets. Les trois premiers elements de cette structure correspondent aux indices des trois sommets definissant la premiere facette de l'objet. L'ordre des indices des sommets au sein de cette structure suit ainsi l'ordre des facettes contenues dans la structure _vectFaceSet.
La structure _vectNormals contient les coordonnees des normales des sommets de l'objet visualise. Les premier elements de _vectNormals correspond aux coordonnees en x, y, z de la normale du premier sommet, et ainsi de suite. Les donnees de cette structure sont calculees a partir des coordonnees de positions des sommets (voir Lissage des normales des sommets).
La structure _vectTexture contient les coordonnees de texture des sommets de l'objet visualise.
La structure P qui contient les coordonnees 3D des sommets de l objet.
Ces differentes structures sont ainsi employees pour creer l objet m_objetSimule de type Mesh (dans la methode initMeshObjet()).

Representation d'un objet de la scene pour l'animer

Les objets simules sont de type ObjetSimule comportant les elements suivants :

Le tableau P (de type std::vector<Vector>) qui contient les coordonnees de positions des particules constituant l'objet a simuler. Ce tableau est initialise a partir du fichier de donnees correspondant rattache a l'objet. Pour permettre l acces aux coordonnees de position pour l affichage des objets, le tableau P est en fait mis dans la structure Noeud. Le premier element de P (de type Vector) correspond ainsi a la coordonnee en x, y et z de la position du premier sommet de l'objet visualise. L'element suivant correspond a la coordonnee en x, y, et z du deuxieme sommet, et ainsi de suite. Les valeurs de ce tableau sont mises a jour a chaque pas de temps de la simulation.
Le tableau V (de type std::vector<Vector>) qui contient les coordonnees de vitesses des particules constituant l'objet a simuler. Les elements de ce tableau sont initialises a zero au depart et sont mises a jour a chaque pas de temps de la simulation.
Le tableau A (de type std::vector<Vector>) qui contient les coordonnees des accelerations des particules constituant l'objet a simuler. Les elements de ce tableau sont initialises a zero au depart et sont mis a jour a chaque pas de temps de la simulation.
Le tableau Force (de type std::vector<Vector>) qui contient les coordonnees des forces appliquees aux particules constituant l'objet a simuler. Les elements de ce tableau sont initialises a zero au depart et sont mis a jour a chaque pas de temps de la simulation.
Le tableau M (de type std::vector<float>) qui contient les mases des particules constituant l'objet a simuler. Ce tableau est initialise a partir du fichier de donnees correspondant rattache a l'objet.

Pour un objet simule de type ObjetSimuleMSS qui est ainsi represente par un systeme masses-ressorts, nous utilisons un element appele _SytemeMasseRessort de type MSS.

La structure MSS permet ainsi de definir le systeme masses-ressorts de l'objet. La structure MSS contient ainsi une liste de Ressort, une liste de Particule.
- la structure Particule (definition physique d'une particule) est constituee d'un identifiant, d'une position, et de la liste des ressorts auxquels la particule est reliee.
- la structure Spring permet de stocker les caracteristiques physiques des ressorts (raideur, amortissement, longueur au repos et viscosite)
- la structure Ressort permet de donner la definition geometrique d'un ressort. Elle est constituee d'un identifiant, d'un Spring contenant ces proprietes, et des deux indices des particules auxquelles le ressort est relie.
- A noter que pour le moment, tous les ressorts d'un meme objet ont les memes caracteristiques physiques definies par l'utilisateur. Il sera possible d'ajouter ulterieurement ces caracteristiques pour chacun des ressorts constituant le systeme masses-ressorts en les mettant par exemple dans un fichier de donnees. Ce systeme masses-ressorts est cree lors de l'initialisation de l'objet simule, notamment a partir du fichier des facettes fourni en parametre de l'objet a simuler. Ce maillage est utilise pour connaitre les interactions qui existent entre les particules d'un objet donne.

La class SolveurExpl permet de gerer un solveur suivant la methode d'Euler semi-implicite.

La methode CalculAccel_ForceGravite rajoute la force de gravite a l ensemble des forces calculees, puis calcul l acceleration des particules.
La methode Solve calcul les vitesses et positions des particules avec le schema d integration numerique d Euler semi-implicite.

La class SolveurImpl permet de gerer un solveur suivant la methode d'Euler implicite.

La methode CalculAccel_ForceGravite rajoute la force de gravite a l ensemble des forces calculees, puis calcul l acceleration des particules.
La methode Solve calcul les vitesses et positions des particules avec le schema d integration numerique d Euler implicite.

Algorithmes de la simulation

Boucle de la simulation

A chaque pas de temps, les calculs suivants sont effectues pour un objet donne :

Calcul des forces appliquees aux particules constituant l'objet
Calcul des accelerations des particules
Calcul des vitesses et des positions des particules

Calcul des forces

Les forces f appliquees aux particules constituant un objet sont dues a la gravite du milieu ainsi qu'aux interactions des autres particules constituant l'objet. La force appliquee a la ieme particule du systeme peut ainsi etre formulee par :

$\vec{f}_i(t) = \sum_{j\mid(i,j)\in E} \left[\vec{f}^{e}_{i,j}(t) + \vec{f}^{v}_{i,j}(t) \right] \: + m_i \vec{g} +\: \vec{f}_{externe}(t),$

avec :

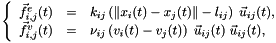
$\left\{ \begin{array}{lcl} \vec{f}^{e}_{i,j}(t) &=& k_{ij} \left(\|x_i(t) - x_j(t)\| - l_{ij}\right)\; \vec{u}_{ij}(t),\\ \vec{f}^{v}_{i,j}(t) &=& {\nu}_{ij} \left(v_i(t) - v_j(t)\right) \; \vec{u}_{ij}(t) \; \vec{u}_{ij}(t), \end{array} \right.$

ou :

E represente l'ensemble des aretes du systeme a particules,
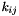$k_{ij}$ est la constante de raideur des ressorts,
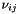${\nu}_{ij}$ est la constante d'amortissement des ressorts,
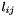$l_{ij}$ est la longueur du ressort au repos reliant la particule i et la particule j,
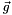$\vec{g}$ represente le vecteur de la gravite,
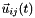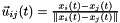et $\vec{u}_{ij}(t)$ est un vecteur unitaire defini par $\vec{u}_{ij}(t) = \frac{x_i(t) - x_j(t)}{\|x_i(t) - x_j(t)\|}$ .

Pour des raisons d'implementation, les forces dues a la gravite sont en fait ajoutees dans le calcul des accelerations.

Calcul des accelerations

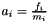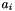Les accelerations des particules sont obtenues a partir de leurs forces en utilisant la loi fondamentale de la dynamique, avec $a_i = \frac{f_i}{m_i}$ ou $a_i$ est l'acceleration de la particule i, 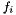$f_i $ la force appliquee sur cette particule, et 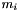$m_i $ sa masse.

C'est au sein de cette methode que le vecteur des forces est reinitialise.

Calcul des vitesses et des positions

Les vitesses et les positions des particules sont obtenues en utilisant la methode explicite de Leap-Frog Verlet :

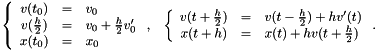
$\begin{array}{lr} \left\{ \begin{array}{ccl} v(t_0) &=& v_0\\ v(\frac{h}{2}) &=& v_0 + \frac{h}{2}v'_0\\ x(t_0) &=& x_0 \end{array} \right., & \left\{ \begin{array}{ccl} v(t+\frac{h}{2}) &=& v(t-\frac{h}{2}) + hv'(t) \\ x(t+h) &=& x(t) + hv(t+\frac{h}{2}) \end{array} \right.. \end{array}$

Calculs effectues pour la visualisation

Calcul de la normale d'une face

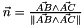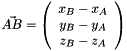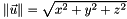Considerons une facette definie par les sommets A, B et C. La normale de cette facette est alors definie par $\vec{n} = \frac{\vec{AB} \wedge \vec{AC}}{\| \vec{AB} \wedge \vec{AC} \|}$ avec $\vec{AB} = \left( \begin{array}{c} x_B - x_A\\ y_B - y_A \\ z_B - z_A \end{array} \right)$ et $\|\vec{u}\| = \sqrt{x^2 + y^2 + z^2}$ ou x, y et z sont les coordonnees de $\vec{u}$ .

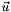Lissage des normales des sommets

Afin d'eviter d'avoir des "pics" entre les facettes, il faut lisser les normales des sommets. Voici les etapes de ce lissage :

La premiere etape consiste a initialiser a zero la normale en chacun des sommets du maillage.
Ensuite pour chacune des facettes, nous allons
calculer sa normale (voir Calcul de la normale d'une face),
et ajouter cette valeur a la normale de chacun des sommets constituant la facette.
Enfin la normale calculee pour chaque sommet est normalisee en la divisant par sa norme.