Wavejets: A Local Frequency Framework for Shape Details Amplification
Back
Paper (71Mo) Supplementary Octave/Matlab partial code
Our paper was awarded an honorable mention of the Gunter Enderle award at Eurographics 2018
Abstract
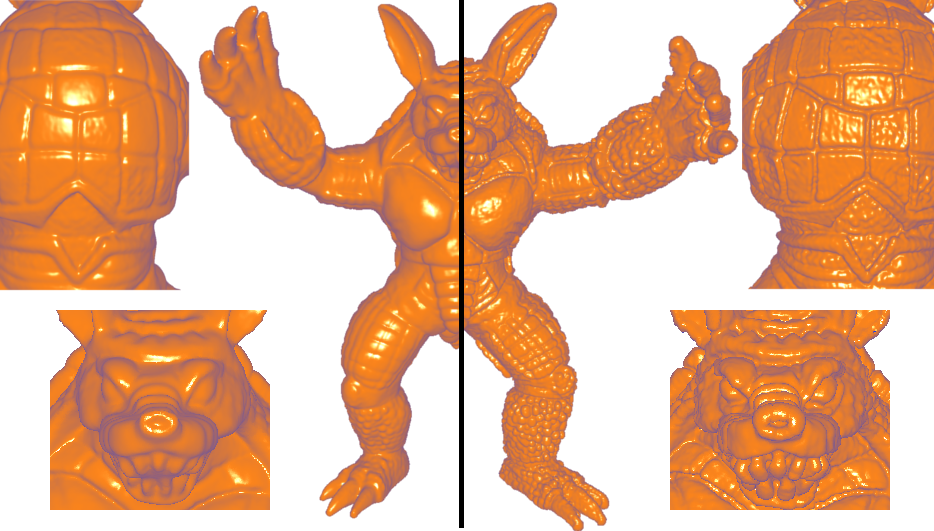
Detail enhancement is a well-studied area of 3D rendering and image processing, which has few equivalents for 3D shape processing. To enhance details, one needs an efficient analysis tool to express the local surface dynamics. We introduce Wavejets, a new function basis for locally decomposing a shape expressed over the local tangent plane, by considering both angular oscillations of the surface around each point and a radial polynomial. We link the Wavejets coefficients to surface derivatives and give theoretical guarantees for their precision and stability with respect to an approximate tangent plane. The coefficients can be used for shape details amplification, to enhance, invert or distort them, by operating either on the surface point positions or on the normals. From a practical point of view, we derive an efficient way of estimating Wavejets on point sets and demonstrate experimentally the amplification results with respect to noise or basis truncation.



Bibtex
@article {Bearzi2018,
author = {Béarzi, Yohann and Digne, Julie and Chaine, Raphaëlle},
title = {Wavejets: A Local Frequency Framework for Shape Details Amplification},
journal = {Computer Graphics Forum, Proc. Eurographics 2018},
year = {2018},
}
Acknowledgements
Research funded by ANR, PAPS project (ANR-14-CE27-0003)