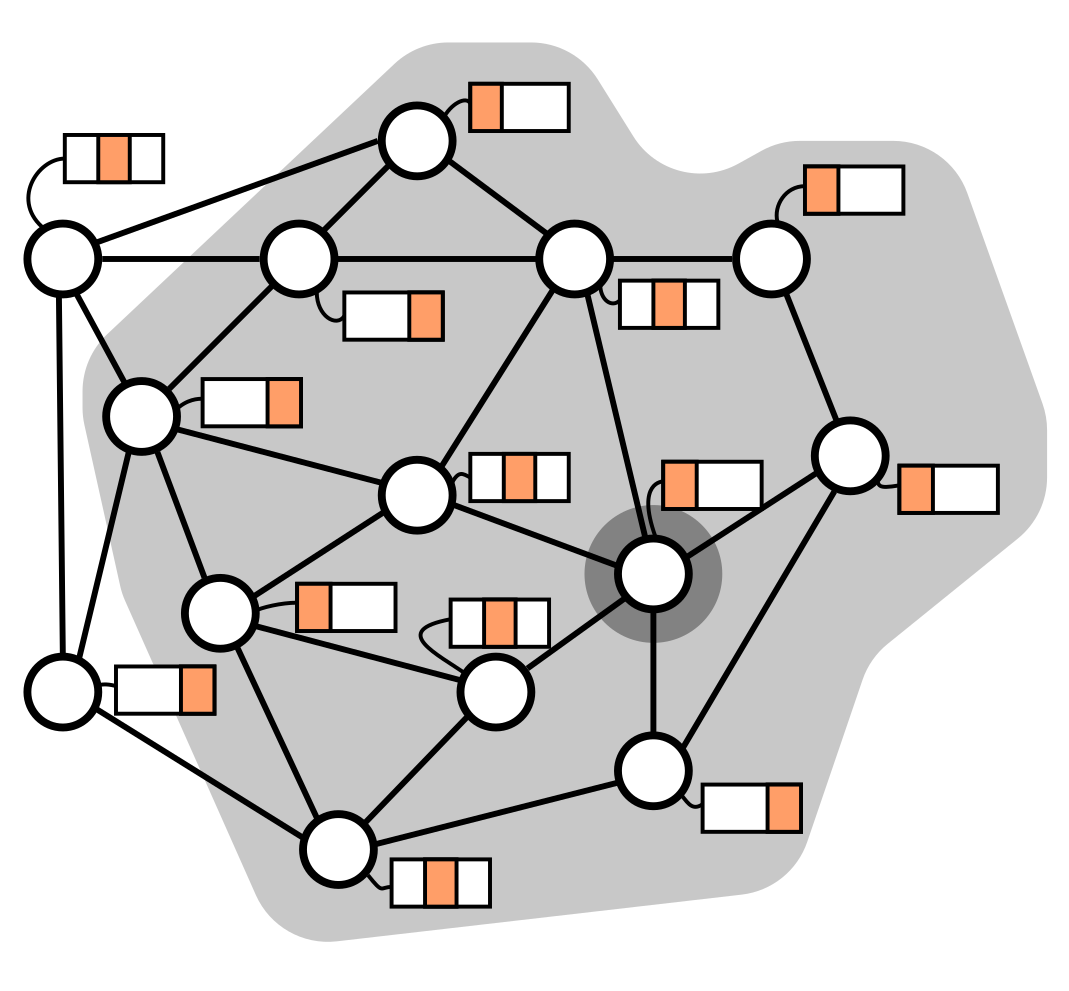
Distributed proofs are mechanisms that enable the nodes of a
network to collectively and efficiently check the correctness of
Boolean predicates on the structure of the network (e.g.,
having a specific diameter), or on objects distributed over the
nodes (e.g., a spanning tree). We consider well known
mechanisms consisting of two components: a
prover that
assigns a
certificate to each node, and a distributed
algorithm called a
verifier that is in charge of
verifying the distributed proof formed by the collection of
all certificates. We show that many network predicates have
distributed proofs offering a high level of redundancy,
explicitly or implicitly.
We use this remarkable property of distributed proofs to
establish perfect tradeoffs between the
size of the
certificate stored at every node, and the
number of rounds of the verification protocol.