Sliced Optimal Transport Sampling
In ACM Transactions on Graphics (Proceedings of SIGGRAPH), 2020
Abstract
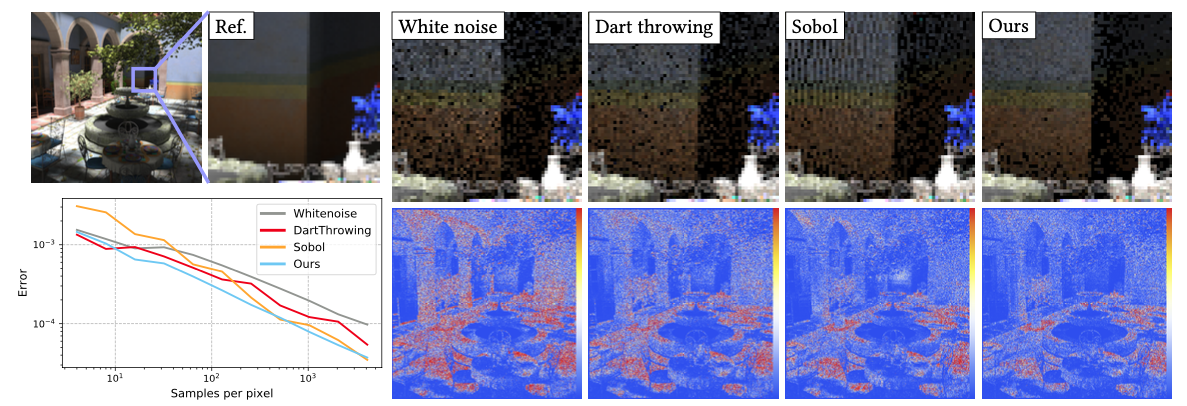
In this paper, we introduce a numerical technique to generate sample distributions in arbitrary dimension for improved accuracy of Monte Carlo integration. We point out that optimal transport offers theoretical bounds on Monte Carlo integration error, and that the recently-introduced numerical framework of sliced optimal transport (SOT) allows us to formulate a novel and efficient approach to generating well-distributed high-dimensional pointsets. The resulting sliced optimal transport sampling, solely involving repeated 1D solves, is particularly simple and efficient for the common case of a uniform density over a d-dimensional ball. We also construct a volume- preserving map from a d-ball to a d-cube (generalizing the Shirley-Chiu mapping to arbitrary dimensions) to offer fast SOT sampling over d-cubes. We provide ample numerical evidence of the improvement in Monte Carlo integration accuracy that SOT sampling brings compared to existing QMC techniques, and derive a projective variant for rendering which rivals, and at times outperforms, current sampling strategies using low-discrepancy sequences or optimized samples.
Downloads
Reference
@article{paulin2020,
author = "Paulin, Loïs and Bonneel, Nicolas and Coeurjolly, David and Iehl, Jean-Claude and Webanck, Antoine and Desbrun, Mathieu and Ostromoukhov, Victor",
title = "Sliced Optimal Transport Sampling",
journal = "{ACM} Transactions on Graphics (Proceedings of SIGGRAPH)",
year = "2020",
volume = "39",
number = "4",
month = jul,
abstract = "In this paper, we introduce a numerical technique to generate sample distributions in arbitrary dimension for improved accuracy of Monte Carlo integration. We point out that optimal transport offers theoretical bounds on Monte Carlo integration error, and that the recently-introduced numerical framework of sliced optimal transport (SOT) allows us to formulate a novel and efficient approach to generating well-distributed high-dimensional pointsets. The resulting sliced optimal transport sampling, solely involving repeated 1D solves, is particularly simple and efficient for the common case of a uniform density over a d-dimensional ball. We also construct a volume- preserving map from a d-ball to a d-cube (generalizing the Shirley-Chiu mapping to arbitrary dimensions) to offer fast SOT sampling over d-cubes. We provide ample numerical evidence of the improvement in Monte Carlo integration accuracy that SOT sampling brings compared to existing QMC techniques, and derive a projective variant for rendering which rivals, and at times outperforms, current sampling strategies using low-discrepancy sequences or optimized samples."
}
Citation(s)
Google scholar citations: ...