Ontologies et Logiques de description¶§
| author: | Pierre-Antoine Champin |
|---|
Historique¶§
Logique¶§
- Logique des propositions (Boole)
- Logique des prédicats (Frege, ...)
- Calculabilité, complexité (Turing-Church)
- Incomplétude (Gödel)
Règles¶§
Clauses de Horn
Systèmes experts (PROLOG)
cretois(minos) . menteur(X) :- cretois(X) . ?- menteur(minos) yes ?- menteur(M) M=minos
Difficulté à maintenir de grosses bases de règles
Remise en ordre¶§
- graphes conceptuels (Sowa)
- représentation graphique formalisée
- logiques de description
- représentation logique simplifiée
Logiques de description¶§
- Pas un langage, mais une famille de langage
- Formalisme de plus haut niveau que la LPO
- Compromis maîtrisé entre décidabilité et complexité
- Autres appellations :
- logiques descriptives
- logiques terminologiques
Ontologies¶§
- Une ontologie est “ une spécification explicite d’une conceptualisation ” (Gruber 1993)
- Modèle de données pour pouvoir
- représenter ce qui existe dans un domaine, et
- raisonner sur ces représentation.
- Notion popularisée avec le Web sémantique et le langage OWL
- lui même basé sur les logique de descriptions
Syntaxe et sémantique¶§
Syntaxe¶§
On utilise ici la syntaxe Manchester de OWL2.
Il existe d’autres syntaxes (XML, RDF), mais elles portent la même sémantique.
Éléments de base¶§
L’univers du discours est constitué d’individus, appartenant à des classes (ou concepts), et reliés entre eux par des propriétés (ou rôles).
| OWL | LPO |
|---|---|
| Individu | Constante |
| Classe | Prédicat 1-aire |
| Propriété | Prédicat 2-aire |
Axiomes¶§
| Syntaxe | Appellation | Sémantique |
|---|---|---|
| C SubClassOf D | subsomption | ∀ x, C(x) → D(x) |
| p SubPropertyOf q | subsomption | ∀ x, y, p(x, y) → q(x, y) |
Exemples
- Crétois SubClassOf Menteur
- ami SubPropertyOf connait
Classes pré-définines¶§
| Syntaxe | Appellation | Sémantique |
|---|---|---|
| Thing | Classe universel (top) | Δ |
| Nothing | Classe absurde (bottom) | ∅ |
Classes complexes : op. ensemblistes¶§
| Syntaxe | Appellation | Sémantique |
|---|---|---|
| not C | complément | { x | ¬C(x) } |
| C or D | union | { x | C(x) } ∪ { x | D(x) } |
| C and D | intersection | { x | C(x) } ∩ { x | D(x) } |
| {a} | extension | {a} |
Exemples
- not Menteur
- Personne or Voiture
- Crétois and Menteur
- Voiture and (Rouge or not Ferrari)
- {john, paul, george, ringo}
Classes complexes : restrictions (1)¶§
| Syntaxe | Appellation | Sémantique |
|---|---|---|
| p some C | qualificateur existentiel | { x | ∃ y, p(x, y) ∧ C(y) } |
| p only C | qualificateur universel | { x | ∀ y, p(x, y) → C(y) } |
| = { x | ∀ y, C(y) ∨ ¬p(x, y) } |
Exemples
- enfant some Personne
- conduit only Ferrari
- (conduit some Voiture) and (conduit only Ferrari)
Note
∀ p, C, (p some C) = not (p only (not C))
ce qui est une autre façon d’expliquer le “paradoxe” de “conduit only Ferrari”
Classes complexes : restrictions (2)¶§
| Syntaxe | Appellation | Sémantique |
|---|---|---|
| p exactly n C | quantificateur (=) | { x | #{y | p(x, y) ∧ C(y)} = n } |
| p max n C | quantificateur (≤) | { x | #{y | p(x, y) ∧ C(y)} ≤ n } |
| p min n C | quantificateur (≥) | { x | #{y | p(x, y) ∧ C(y)} ≥ n } |
NB : on omet généralement C lorsqu’il s’agit de Thing
Exemples
- conduit max 1
- conduit exactly 2 Ferrari
- connait min 2 (Crétois and Menteur)
Classes complexes et axiomes : exemples¶§
| SubClassOf | |
|---|---|
| conduit some Voiture | Adulte |
| inverse conduit some Thing | Véhicule |
| Personne | Adulte or Enfant |
| Personne | père exactly 1 Homme and mère exactly 1 Femme |
| Personne | not Voiture |
Propriétés complexes¶§
| Syntaxe | Appellation | Sémantique |
|---|---|---|
| inverse p | propriété inverse | { (x, y) | p(y, x) } |
| p ∘ q ⁽¹⁾ | propriété composée | { (x, y) | ∃ z, p(x, z) ∧ q(z, y) } |
| ¬p ⁽¹⁾ | complément | { (x, y) | ¬p(x, y) } |
Exemples :
- inverse conduit
- connait ∘ conduit ⁽¹⁾
- (connait ∘ conduit) some Ferrari ⁽¹⁾
⁽¹⁾ pas exprimable directement en syntaxe Manchester (cf. SubPropertyChain, DisjointWith)
Autres types d’axiomes¶§
OWL offre des axiomes « de haut niveau » qui visent à
- améliorer la lisibilité de la base de connaissance
- optimiser le raisonnement
- contraindre l’utilisation de certains constructeurs à certaines formes d’axiome selon les profils (e.g. Property Chain)
Sur les classes¶§
| Axiome | équivalent à |
|---|---|
| C EquivalentTo D | C SubClassOf D et D SubClassOf C |
| C DisjointWith D | C SubClassOf not D |
| C DisjointWith D, E, F... | C, D, E, F... disjointes deux à deux |
| C DisjointUnionOf D, E, F... | C EquivalentTo (D or E or F...) et D, E, F... disjointes deux à deux |
Sur les propriétés¶§
| Axiome | équivalent à |
|---|---|
| p EquivalentTo q | p SubPropertyOf q et q SubPropertyOf p |
| p DisjointWith q | p SubPropertyOf ¬q ⁽¹⁾ |
| p SubPropertyChain q o r o s | p SubPropertyOf q ∘ r ∘ s ⁽¹⁾ |
| p InverseOf q | p EquivalentTo inverse q |
⁽¹⁾ cet énnoncé n’est pas conforme à la syntaxe Manchester
Sur les propriétés (suite)¶§
| Axiome | équivalent à |
|---|---|
| p Transitive | p SubPropertyChain p o p |
| p Symmetric | p SubPropertyOf inverse p |
| p Asymmetric | p DisjointWith inverse p |
| p Functional | Thing SubClassOf p max 1 |
| p InverseFunctional | Thing SubClassOf (inverse p max 1) |
| p Reflexive | Thing SubClassOf p Self |
| p Irreflexive | Thing DisjointWith p Self |
Deux sortes de propriétés¶§
OWL définit en fait deux sortes différentes de propriétés :
- les object properties relient deux individus ;
- les datatype properties relient un individu à une valeur litérale (nombre, chaîne de caractère, booléen...).
Profils OWL 2¶§
| Full | aucune contrainte, indécidable |
| DL | minimum de contraintes, décidable mais très complexe |
| EL | quantifications existentielles (EL++), expressivité adaptée à certains domaines (biologie) |
| QL | peut s’implémenter au dessus d’un langage de requêtes (SQL) |
| RL | peut s’implémenter au dessus d’un langage à base de règles (Datalog) |
Raisonnement¶§
Rappels¶§
- Interprétation de F
- domaine du discours
- fonction d’interprétation
- Modèle
- axiomes → contraintes
- Implication
- F est satisfiable si elle a au moins un modèle
- F ⊧ G ssi tous les modèles de F sont des modèles de G
- ⇒ F ⊧ G ssi F ∧ ¬G est non satisfiable
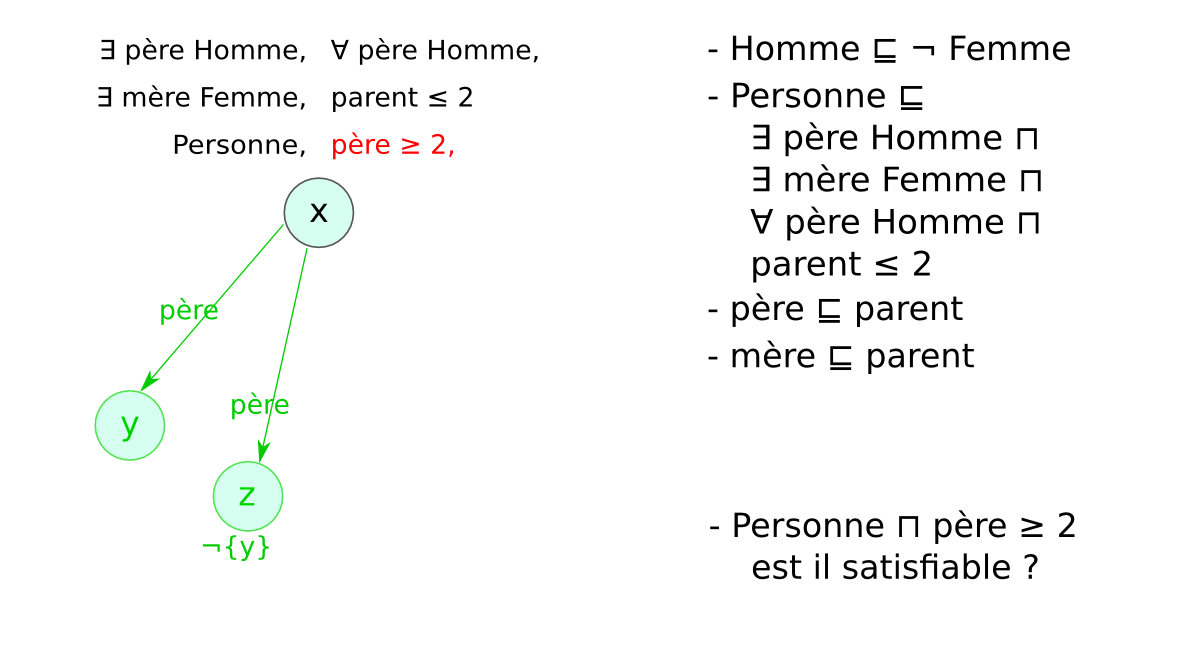
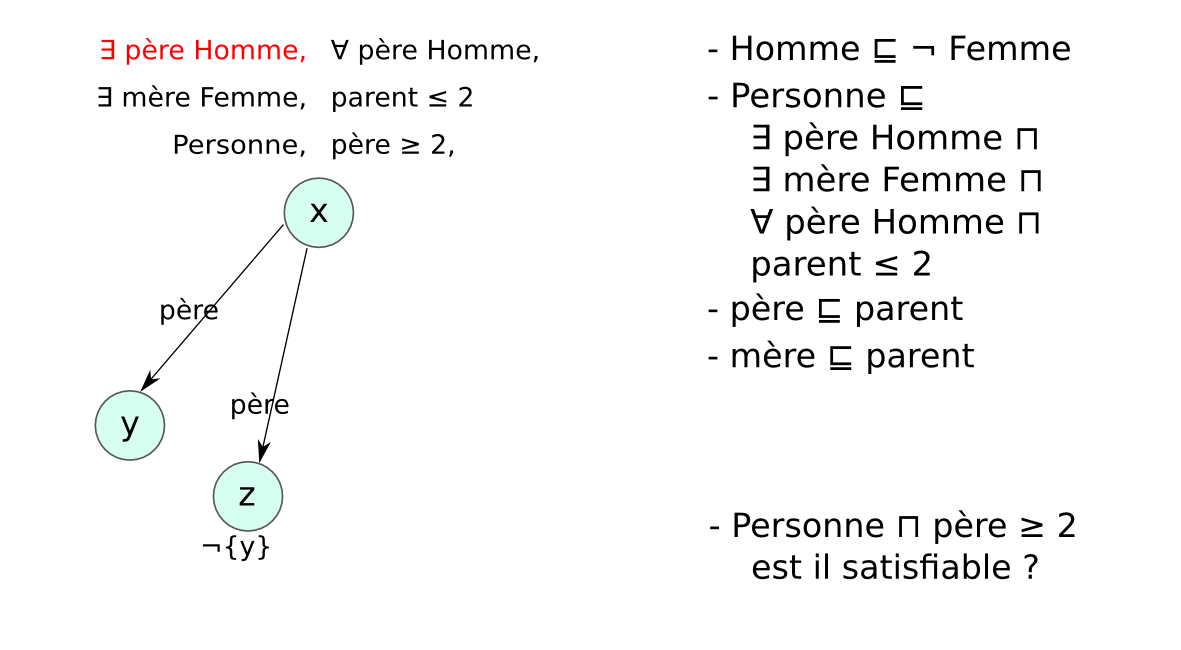
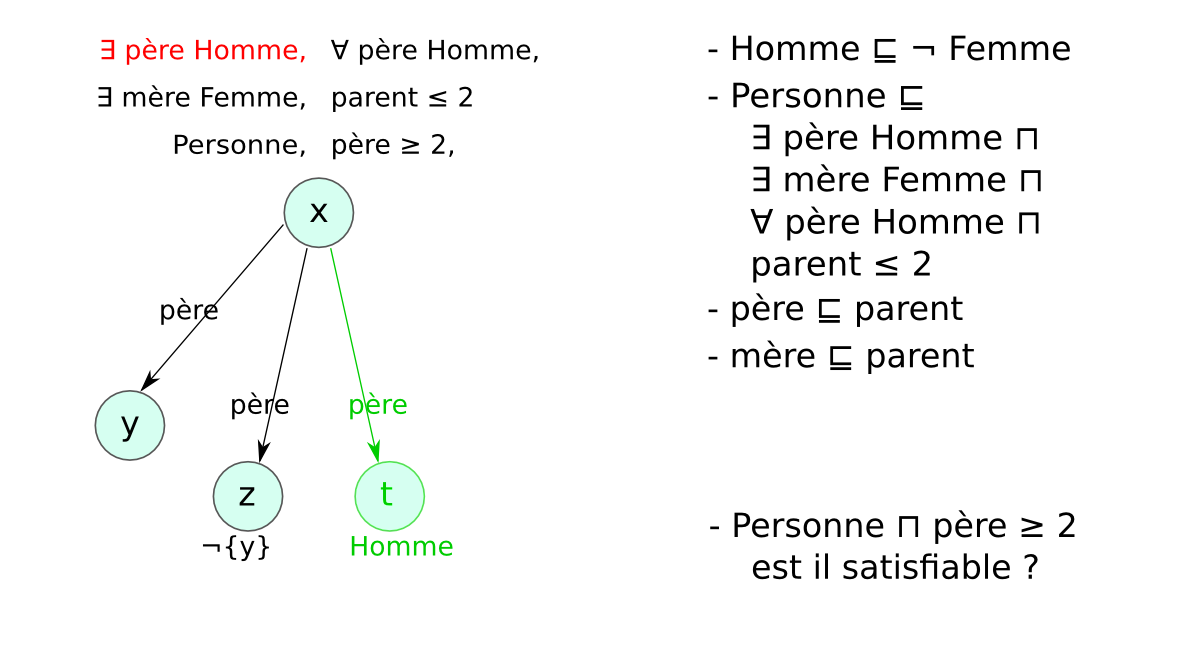
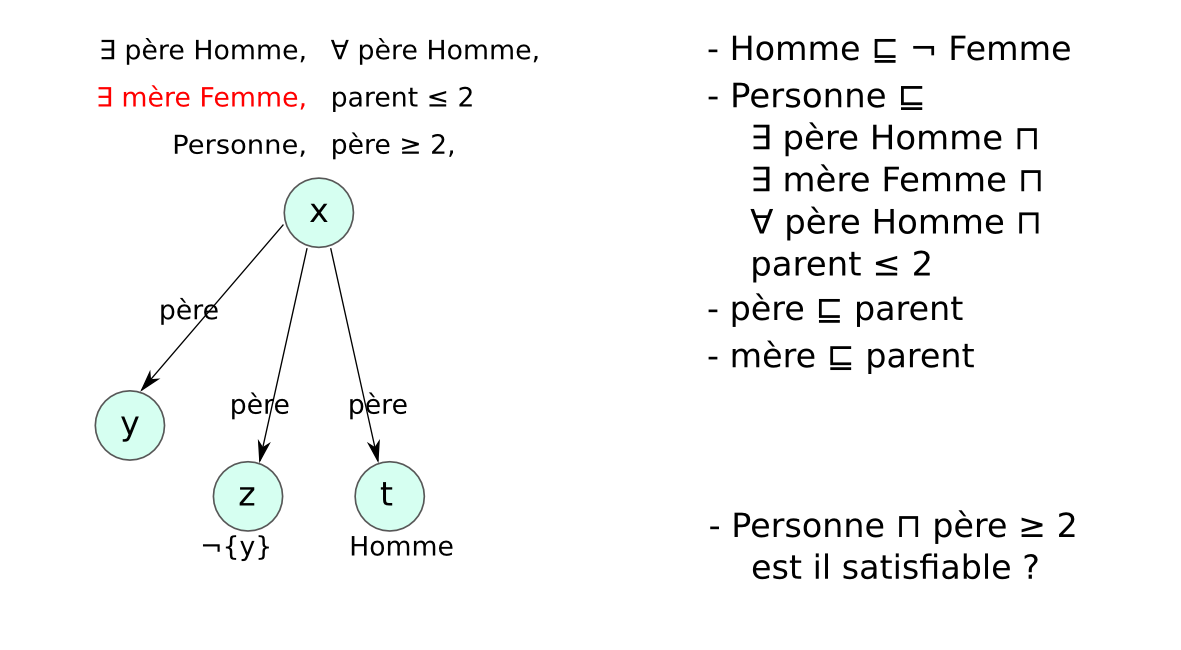
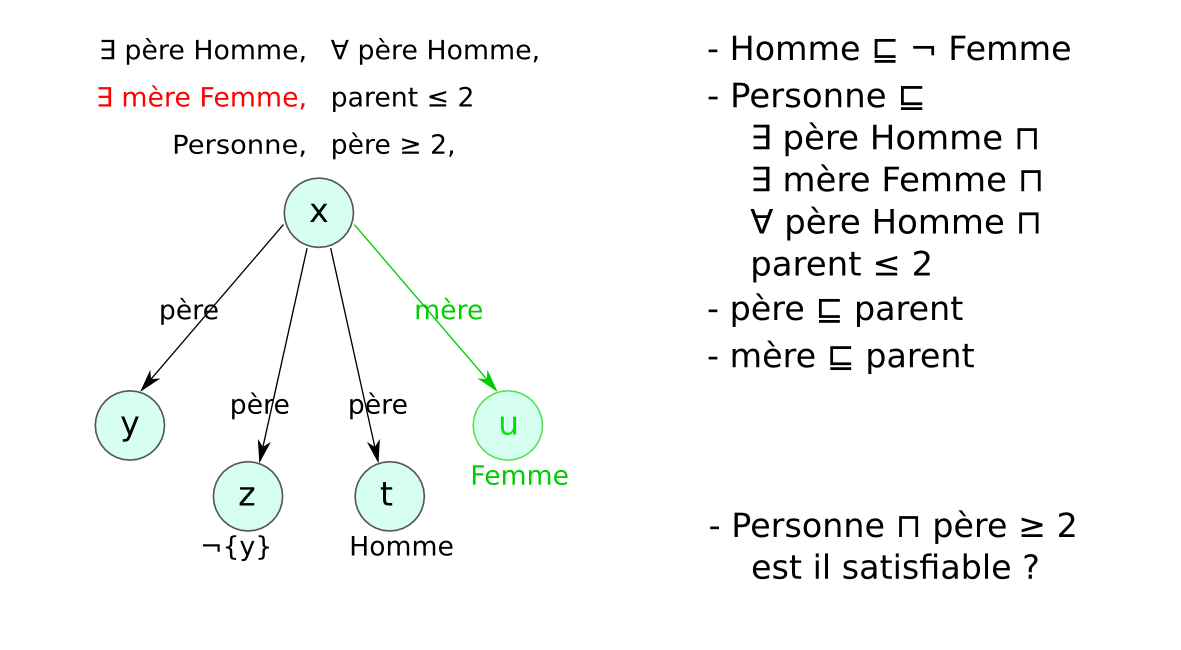
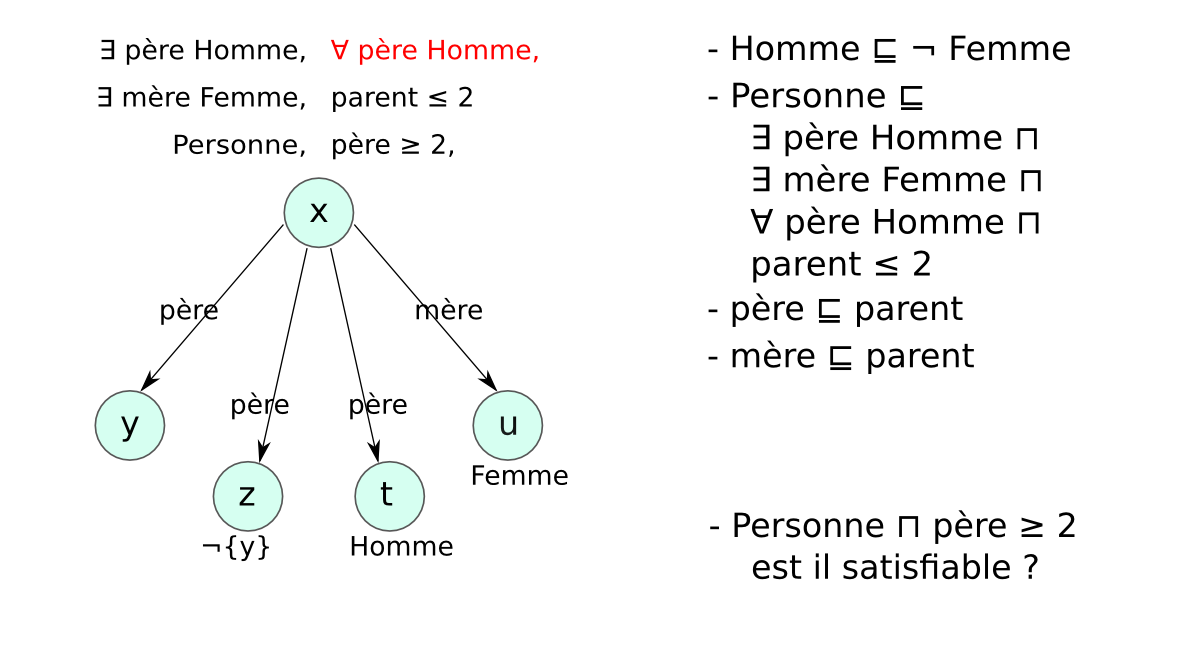
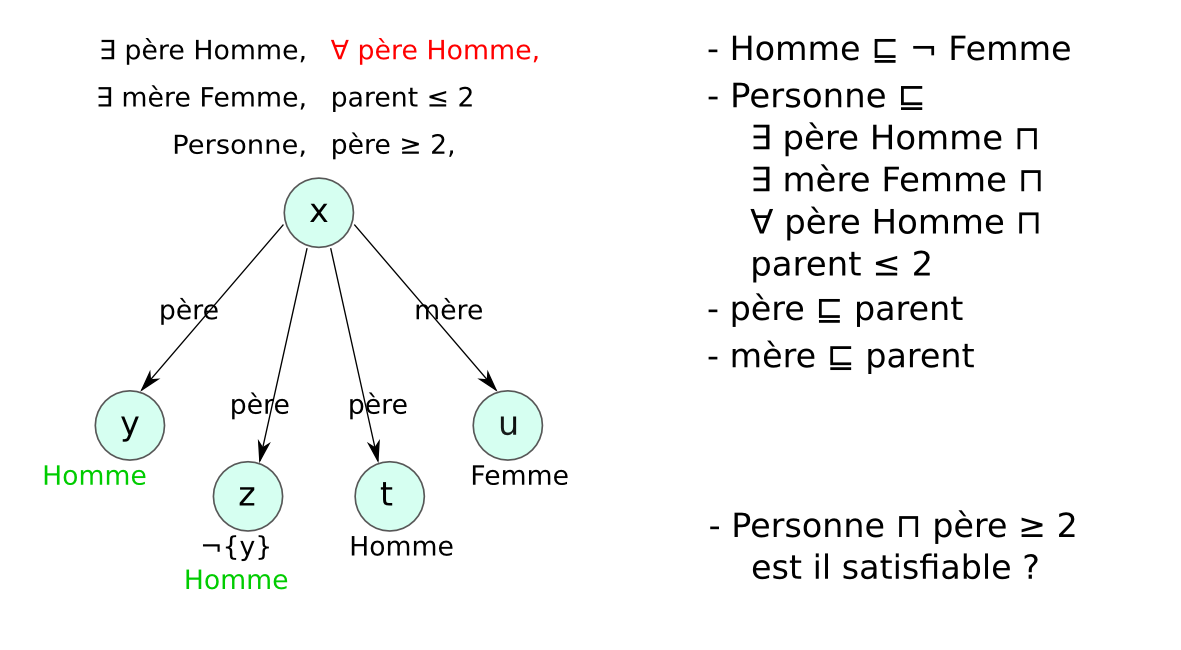
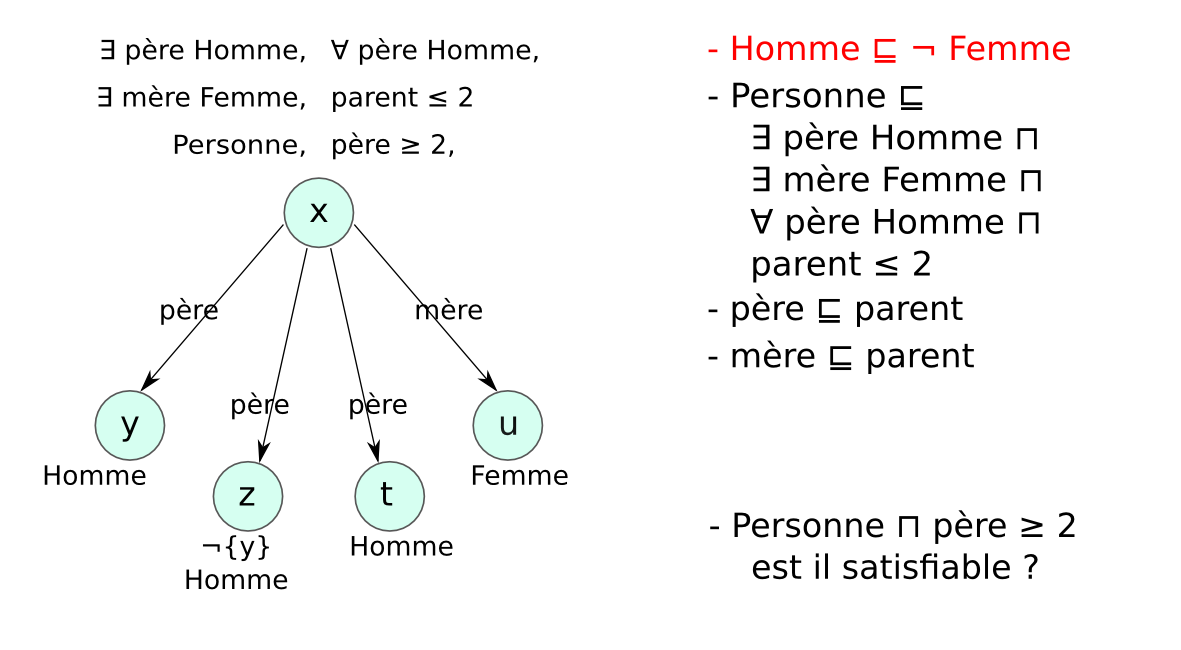
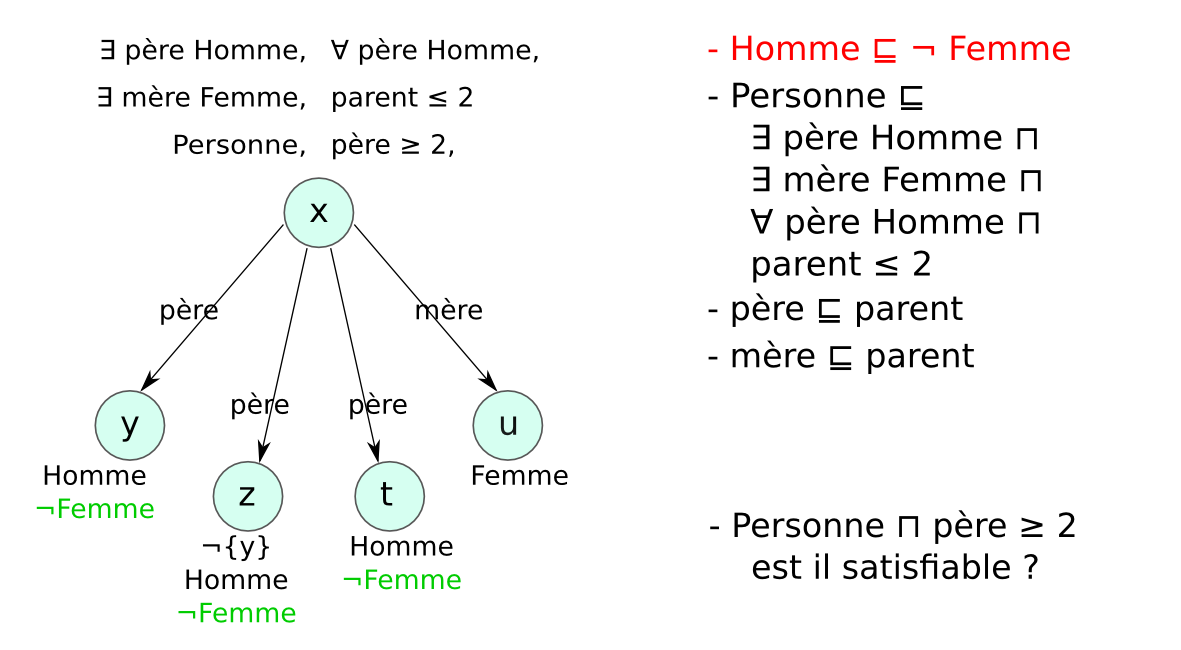
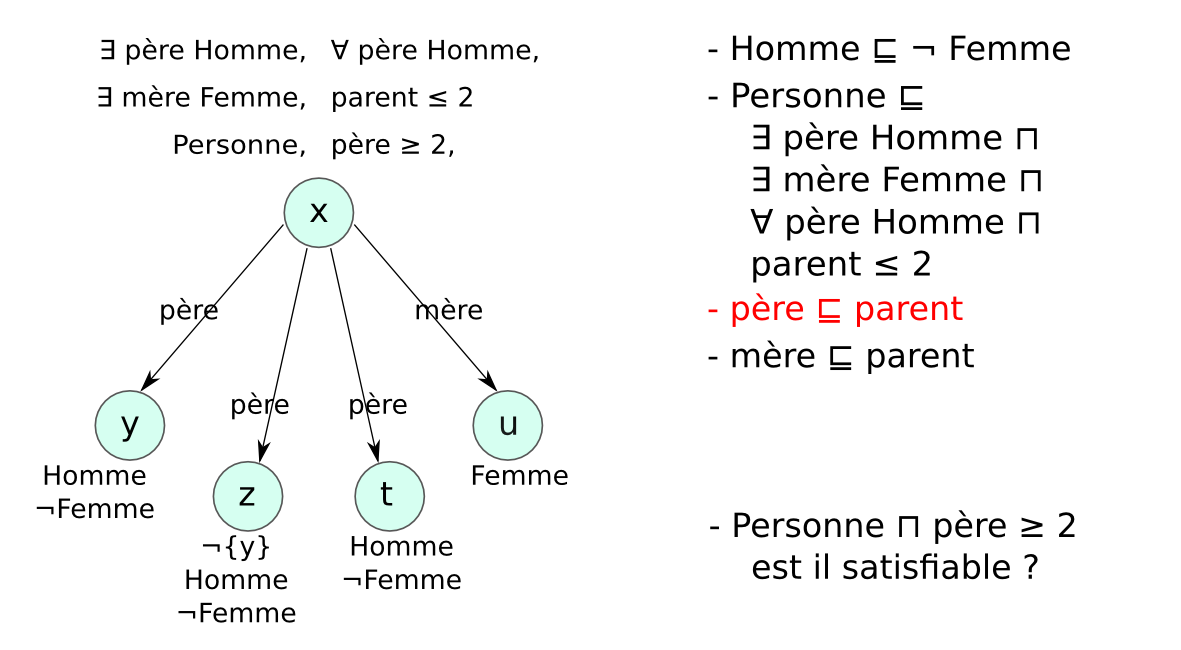
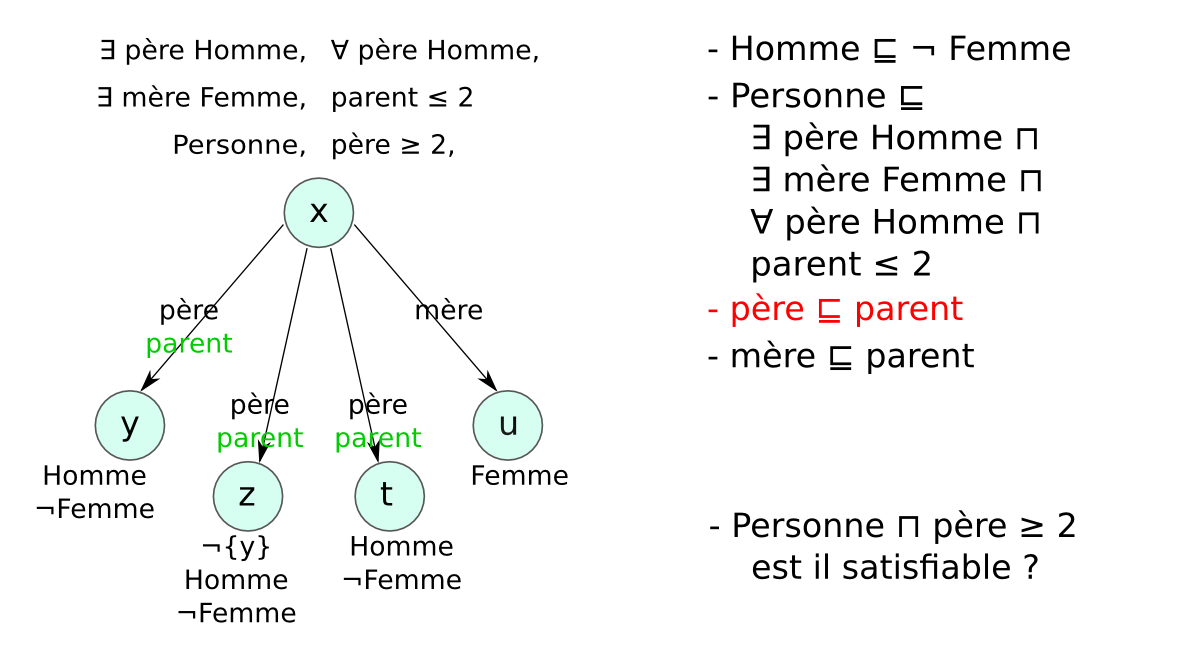
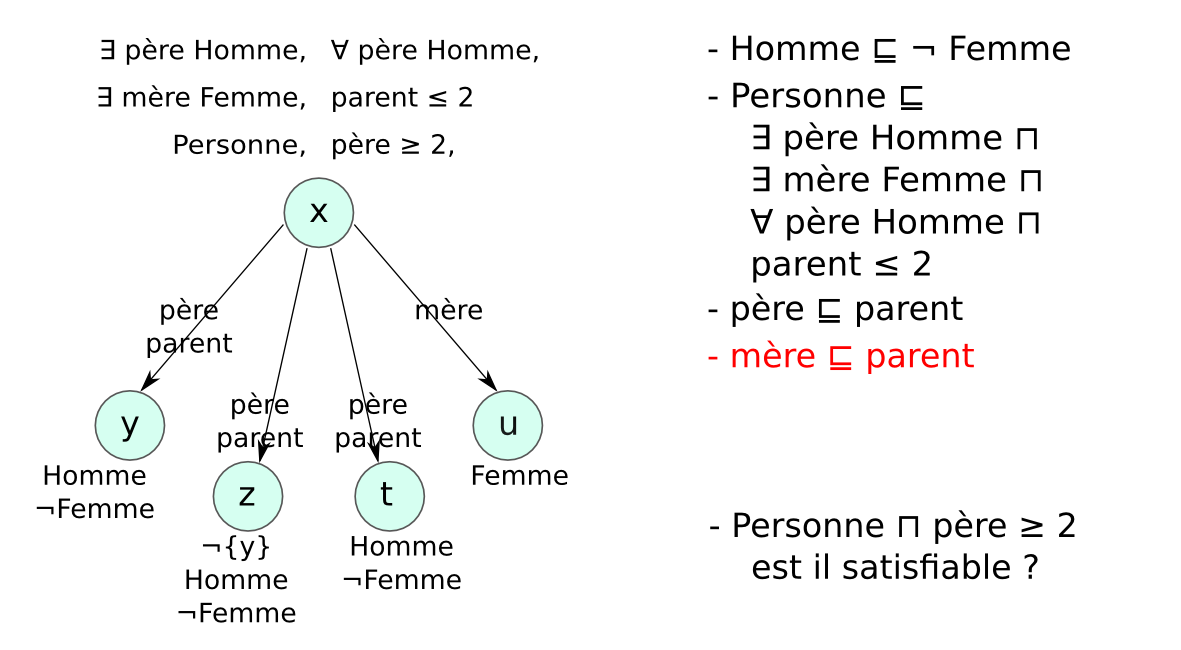
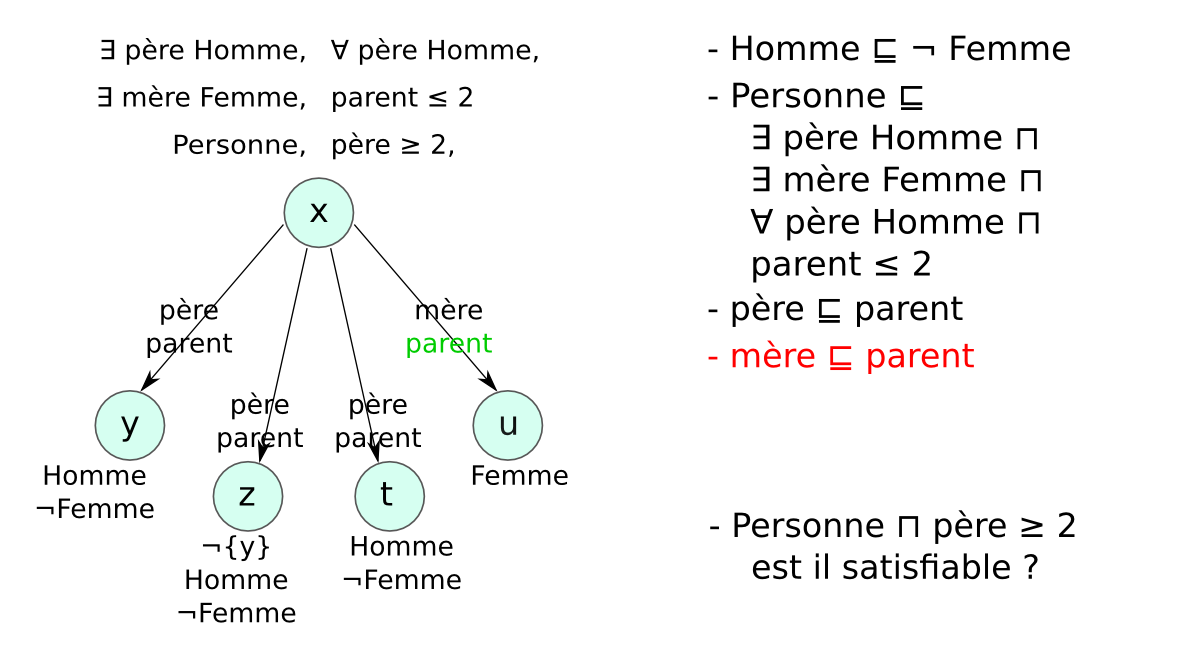
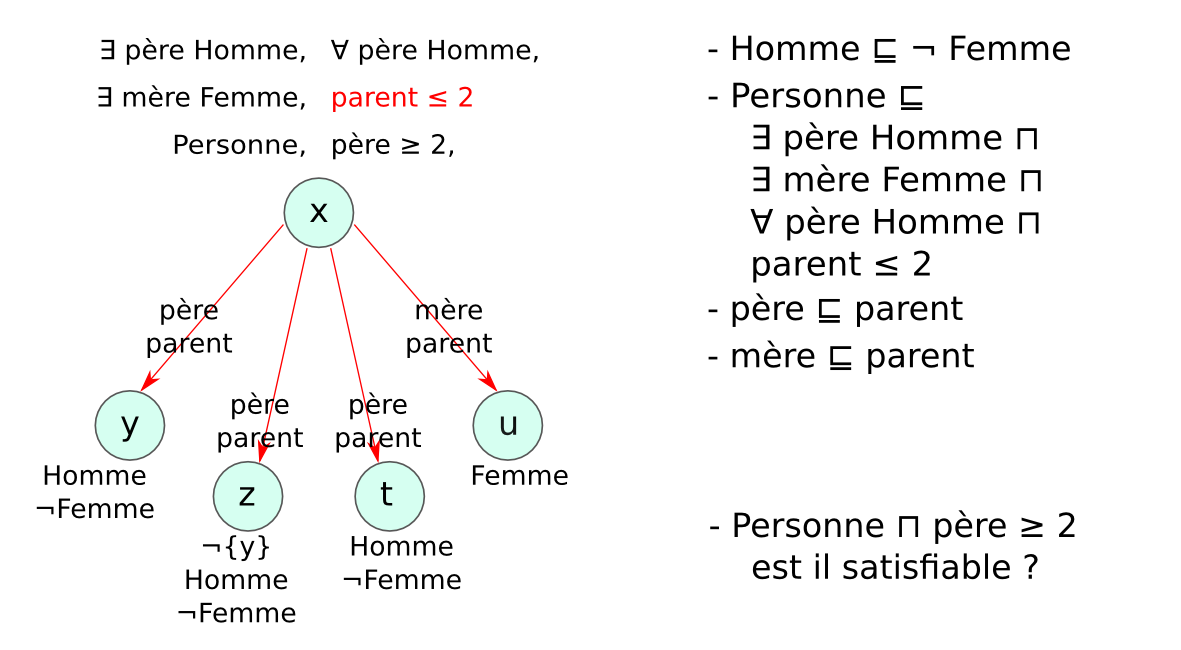
Méthode des tableaux¶§
- Un tableau est un arbre, représentant une famille de modèles
- Application systématique de règles pour explorer tous les modèles possibles (non déterministe)
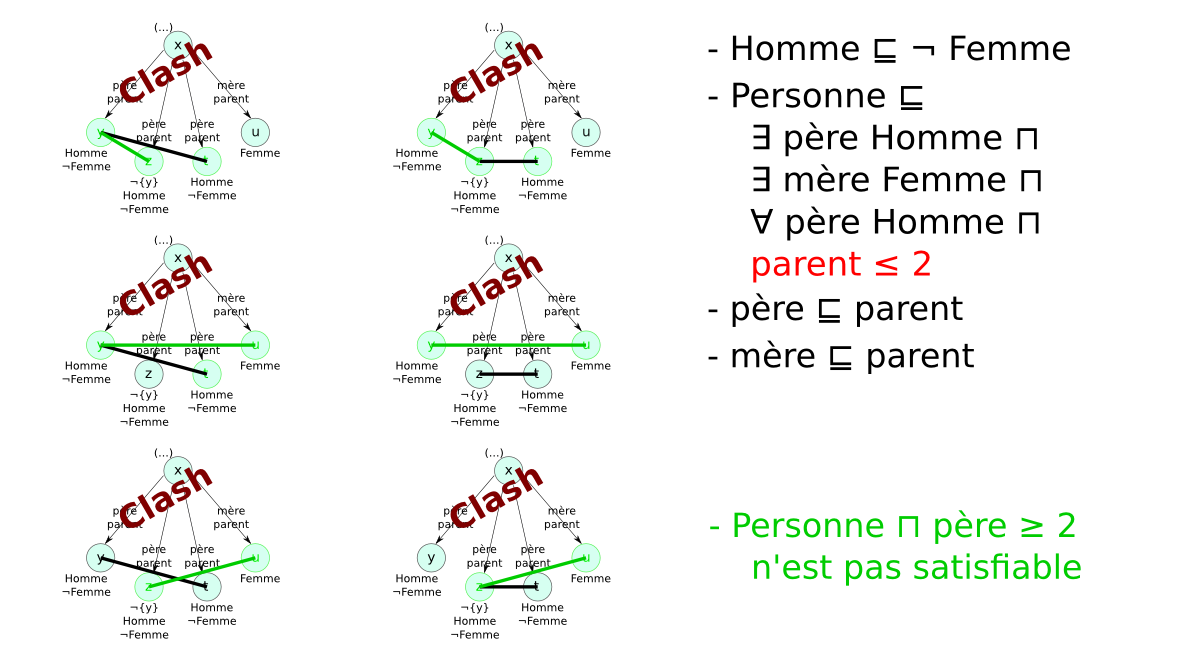
- Preuve par réfutation : classe non satisfiable
- A subClassOf B ⇔ A and not B est non satisfiable
Enjeux¶§
- Décidable : dépend du type de LD choisie
- Correct/complet : ensemble de règles de transformation
- Complexe : optimiser l’ordre d’application des règles
- Problème des modèles infinis : exemple
- Entier ⊑ (= 1 suivant Entier) ⊓ (≤ 1 suivant⁻)
- {zero} ⊑ Entier ⊓ (= 0 suivant⁻)
Méta-modélisation¶§
- En théorie : séparation stricte entre les individus, les classes et les propriétés
- En pratique : pas d’ambiguïté syntaxique sur la nature d’un terme
- Punning (calembour) : autorisation d’utiliser le même terme pour des éléments de nature différente
- aucun lien sémantique entre eux
- mais intérêt pragmatique
- ⚠ pas très bien supporté par Protégé :-(