Logiques de descriptions§

author:Pierre-Antoine Champin

Contrat Creative Commons

Historique§

Logique§

  • Logique des propositions (Boole)
  • Logique des prédicats (Frege, ...)
  • Calculabilité, complexité (Turing-Church)
  • Incomplétude (Gödel)

Règles§

  • Clauses de Horn

  • Systèmes experts (PROLOG)

    cretois(minos) .
menteur(X) :- cretois(X) .

?- menteur(minos)
yes
?- menteur(M)
M=minos

  • Difficulté à maintenir de grosses bases de règles

Logiques « intuitives »§

  • Réseaux sémantiques
    • représentation graphique
_images/reseau_semantique.jpg

Logiques « intuitives » (suite)§

  • Frames (Minsky)

    • approche « objet »

    • stéréotypes

    • valeurs par défaut

    • logique non monotone

      (tous les oiseaux volent, les autruches ne volent pas)

Remise en ordre§

  • graphes conceptuels (Sowa)
    • représentation graphique formalisée
  • logiques de descriptions
    • représentation logique simplifiée

Logiques de description§

  • Pas un langage, mais une famille de langage
  • Formalisme de plus haut niveau que la LPO
  • Compromis maîtrisé entre décidabilité et complexité
  • Autres appellations :
    • logiques descriptives
    • logiques terminologiques

Syntaxe et sémantique§

Éléments de base§

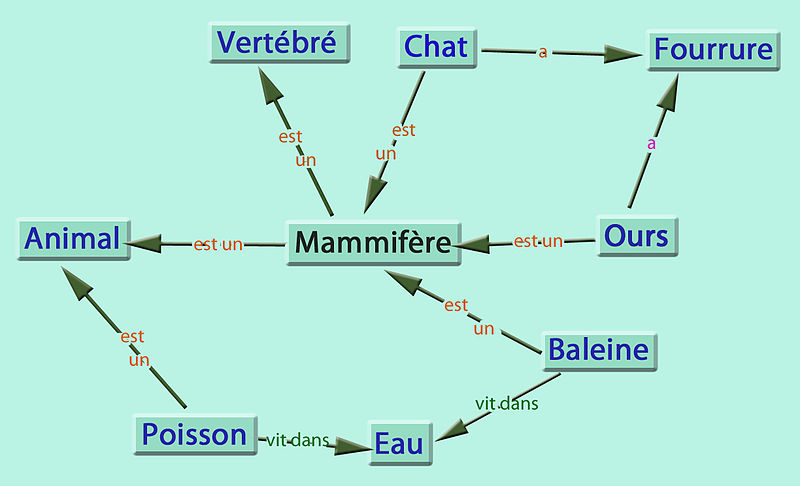
L’univers du discours est constitué d’individus, appartenant à des concepts (ou classes), et reliés entre eux par des rôles (ou propriété).

LD LPO
Individu Terme
Concept Prédicat 1-aire
Rôle Prédicat 2-aire

Exemples§

Concepts Rôles Individus
Homme connait john
Voiture (a pour) père jane
Rouge mère ab-123-cd
Menteur enfant  
Ferrari conduit  

Axiomes§

Syntaxe Appellation Sémantique
C ⊑ D subsomption de concepts ∀ x, C(x) → D(x)
r ⊑ s subsomption de rôles ∀ x, y, r(x, y) → s(x, y)

NB: l’équivalence peut s’exprimer par deux subsomptions symétriques : C ⊑ D et D ⊑ C

Axiomes : exemples§

  • Crétois ⊑ Menteur
  • ami ⊑ connait

Concepts complexes : constructeurs ensemblistes§

Syntaxe Appellation Sémantique
⊤ concept universel (top) Δ
⊥ concept absurde (bottom) ∅
¬C complément { x | ¬C(x) }
C ⊔ D union { x | C(x) } ∪ { x | D(x) }
C ⊓ D intersection { x | C(x) } ∩ { x | D(x) }
{a} extension {a}

Constructeurs ensemblistes : exemples§

  • ¬Menteur
  • Homme ⊔ Voiture
  • Crétois ⊓ Menteur
  • Voiture ⊓ (Rouge ⊔ ¬Ferrari)
  • {john, paul, george, ringo}

Concepts complexes : restrictions§

Syntaxe Appellation Sémantique
∃ r C qualificateur existentiel { x | ∃ y, r(x, y) ∧ C(y) }
∀ r C qualificateur universel { x | ∀ y, ¬r(x, y) ∨ C(y) }
= n r C quantificateur { x | #{y | r(x, y) ∧ C(y)} = n }
≤ n r C quantificateur (max) { x | #{y | r(x, y) ∧ C(y)} ≤ n }
≥ n r C quantificateur (min) { x | #{y | r(x, y) ∧ C(y)} ≥ n }

NB : on omet généralement C lorsqu’il s’agit de ⊤ ; e.g.

∃ r ,  ∀ r ,  = 1 r ...

Restrictions : exemples§

  • ∃ enfant
  • ∀ conduit Ferrari
  • (∃ conduit) ⊓ (∀ conduit Ferrari)
  • = 2 conduit Ferrari
  • ≥ 2 connait (Crétois ⊓ Menteur)

Rôles complexes§

Syntaxe Appellation Sémantique
r⁻ rôle inverse { (x, y) | r(y, x) }
r∘s rôle composé { (x, y) | ∃ z, r(x, z) ∧ s(z, y) }
¬r complément { (x, y) | ¬r(x, y) }

Exemples§

  • conduit⁻
  • connait ∘ conduit
  • connait ∘ connait

Axiomes complexes : exemples§

  • ∃ conduit ⊑ Adulte
  • ∃ conduit⁻ ⊑ Voiture
  • Personne ⊑ Adulte ⊔ Enfant
  • Personne ⊑ (= 1 père Homme) ⊓ (= 1 mère Femme)
  • Personne ⊑ ¬Voiture

Décidabilité et complexité§

Chaque LD impose des contraintes sur :

  • les axiomes autorisés,
  • les constructeurs autorisés,
  • la manière de les combiner,

afin de garantir que les mécanismes de raisonnement

  • seront décidables,
  • auront une complexité maximale.

→ compromis entre expressivité et complexité.

Raisonnement§

Rappels§

  • Interprétation de F
    • domaine du discours
    • fonction d’interprétation
  • Modèle
    • axiomes → contraintes
  • Implication
    • F est satisfiable si elle a au moins un modèle
    • F ⊧ G ssi tous les modèles de F sont des modèles de G
    • ⇒ F ⊧ G ssi F ∧ ¬G est non satisfiable

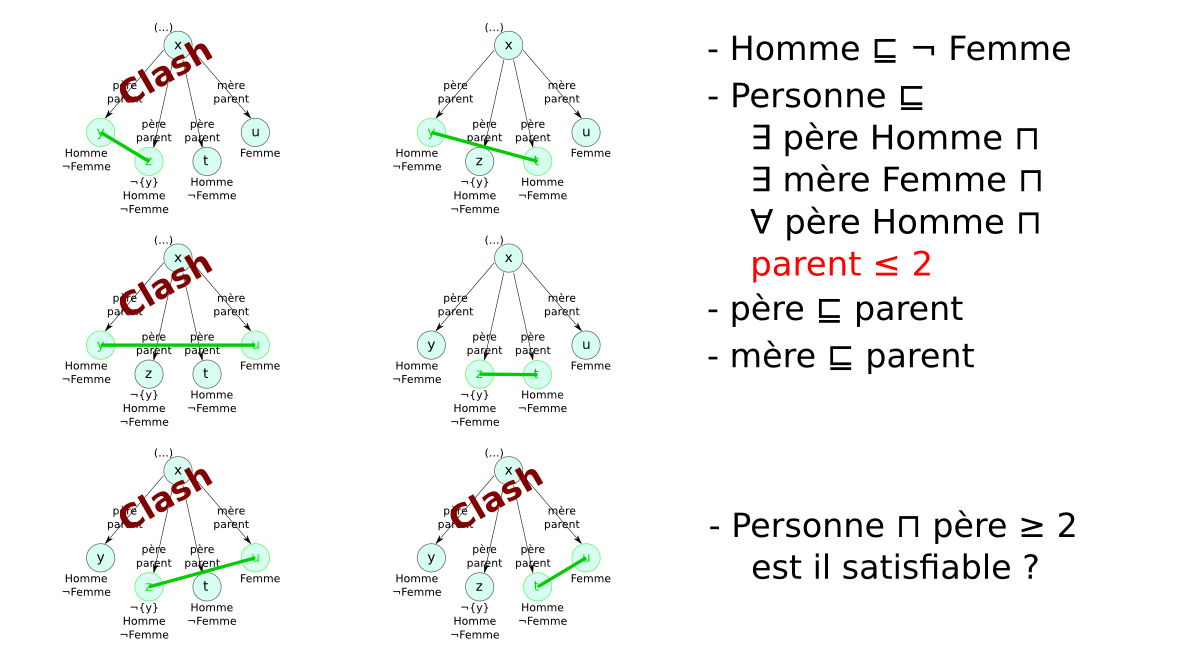
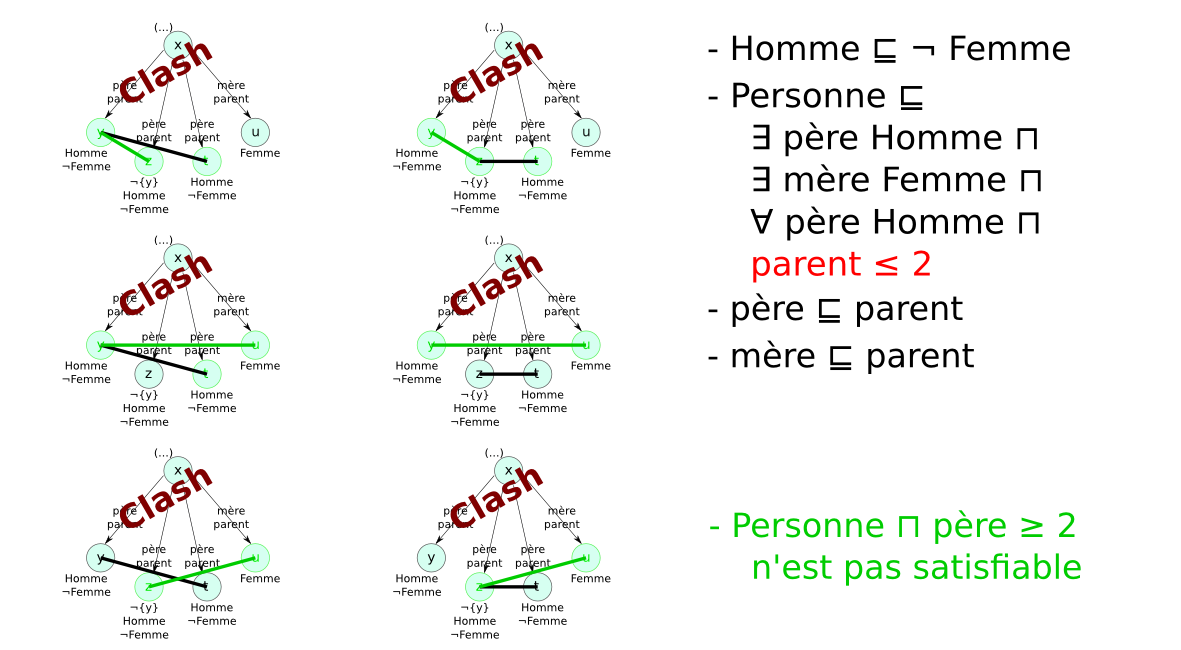
Méthode des tableaux§

  • Un tableau est un arbre, représentant une famille de modèles
  • Application systématique de règles pour explorer tous les modèles possibles (non déterministe)
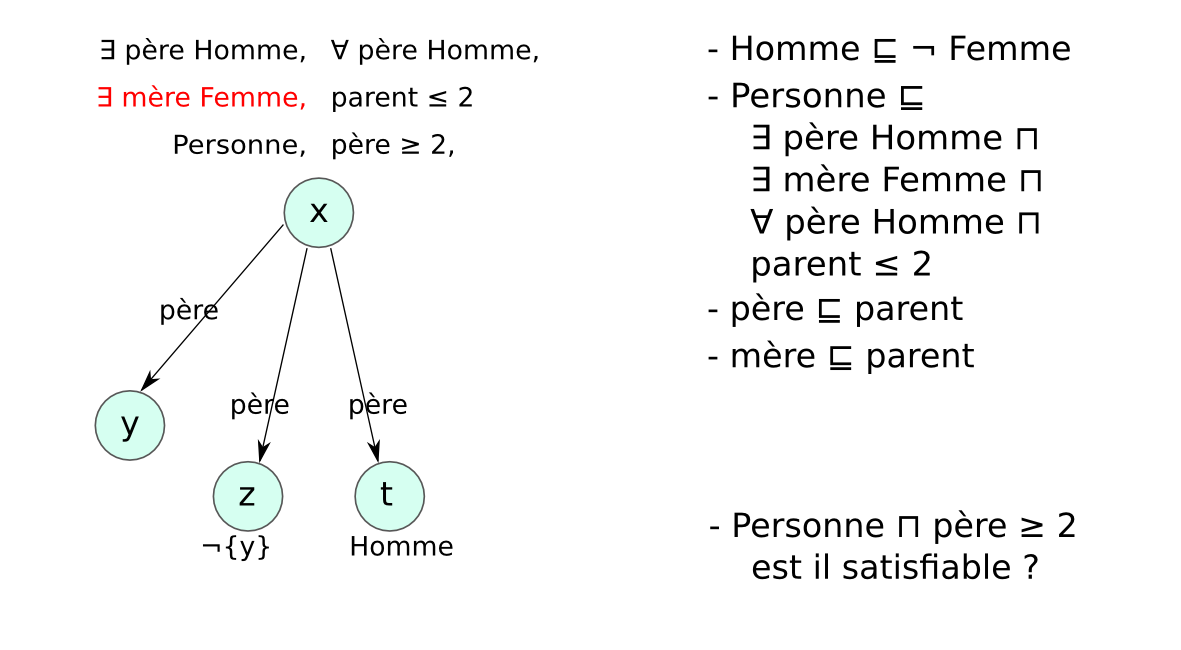
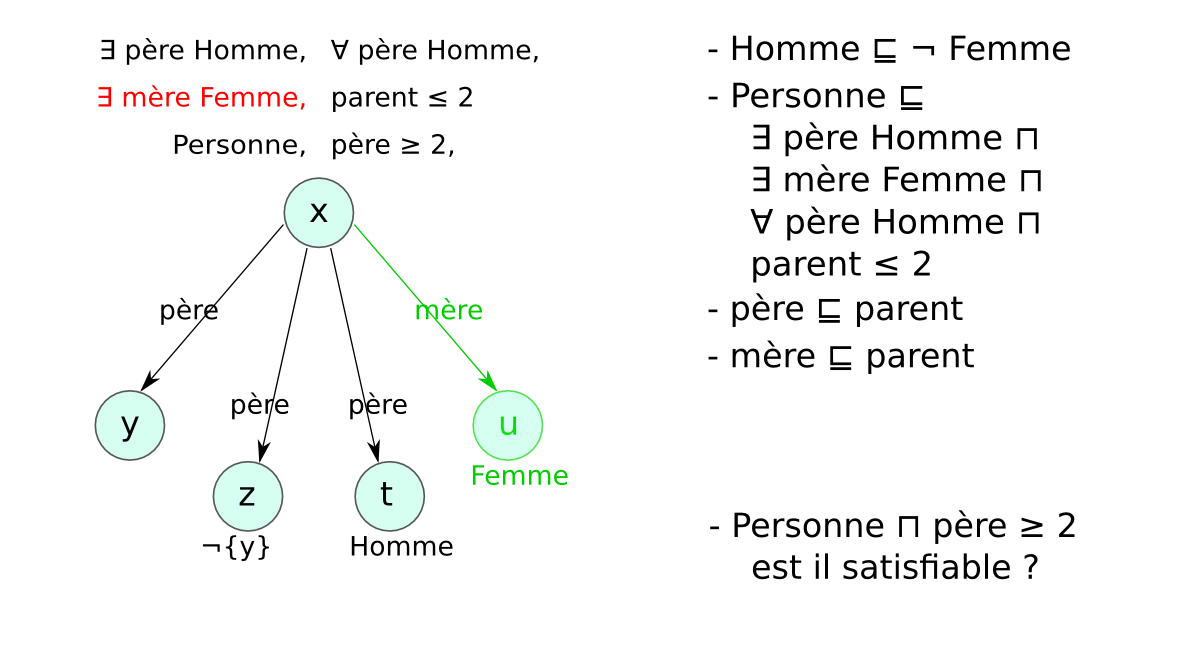
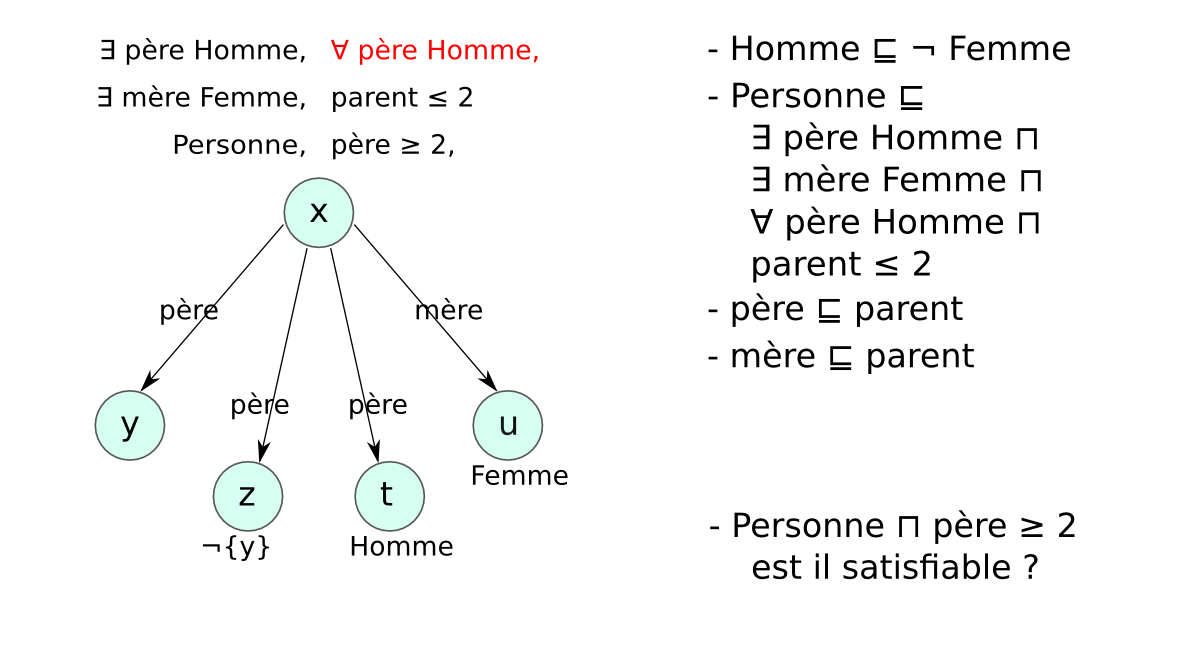
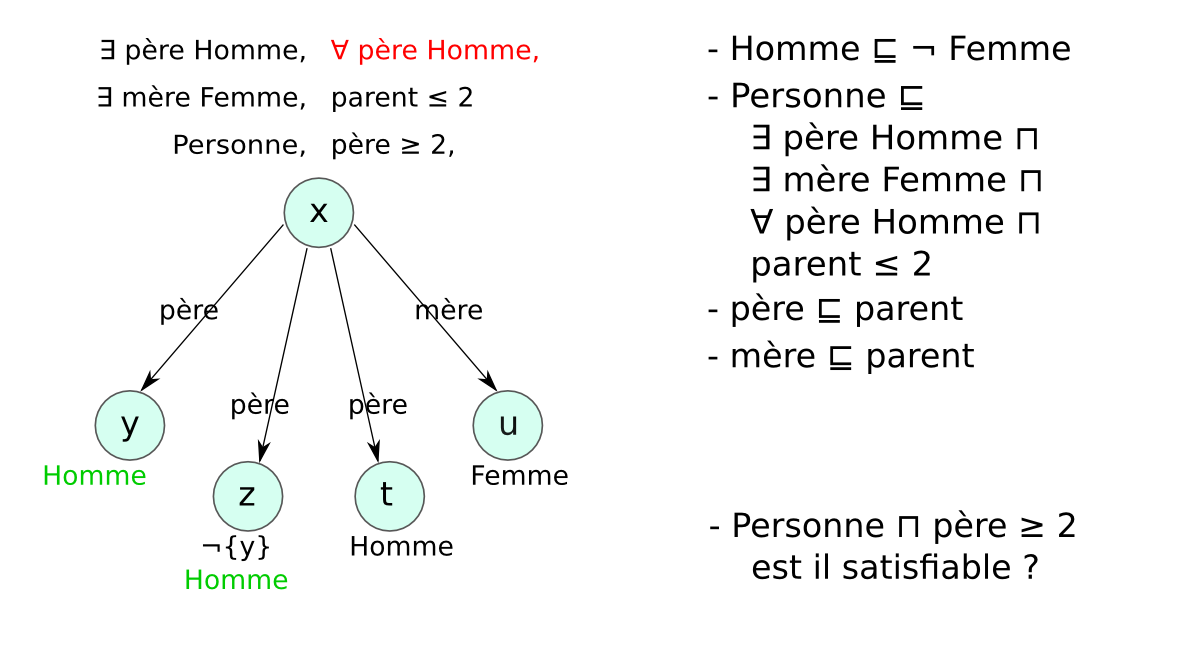
  • Preuve par réfutation : concept non satisfiable

Exemple§

_images/Frame00.png _images/Frame01a.png _images/Frame01b.png _images/Frame02a.png _images/Frame02b.png _images/Frame03a.png _images/Frame03b.png _images/Frame04a.png _images/Frame04b.png _images/Frame05a.png _images/Frame05b.png _images/Frame06a.png _images/Frame06b.png _images/Frame07a.png _images/Frame07b.png _images/Frame08a.png _images/Frame08b.png _images/Frame09a.png _images/Frame09b.png _images/Frame09c.png

Enjeux§

  • Décidable : dépend du type de LD choisie
  • Correct/complet : ensemble de règles de transformation
  • Complexe : optimiser l’ordre d’application des règles
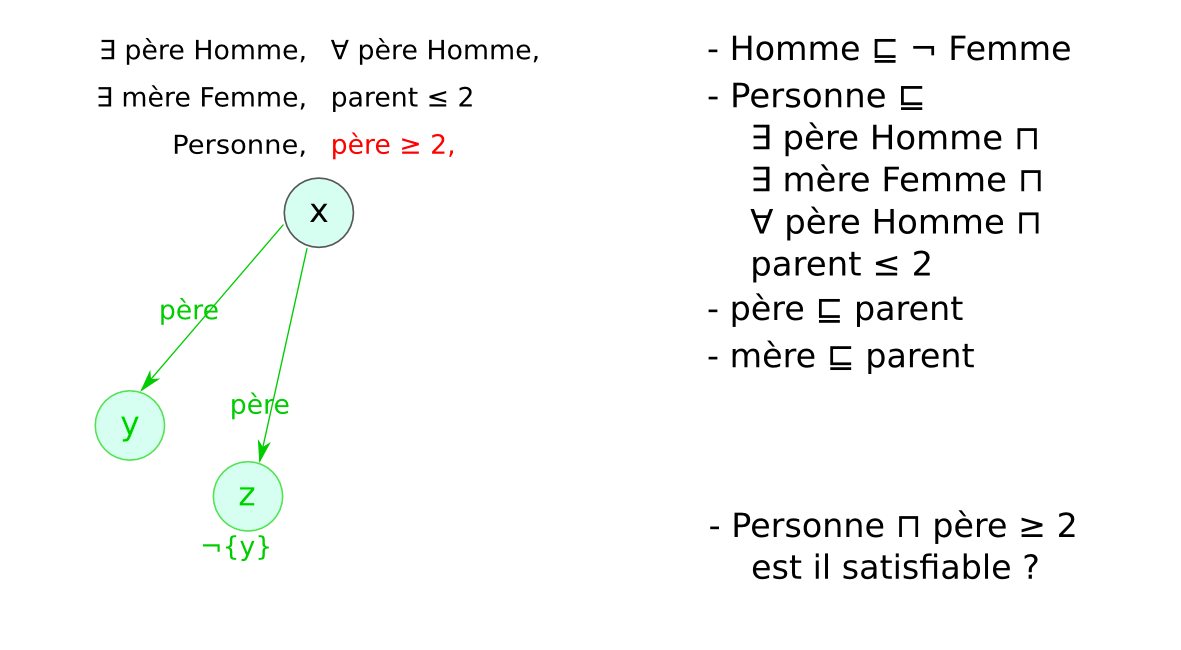
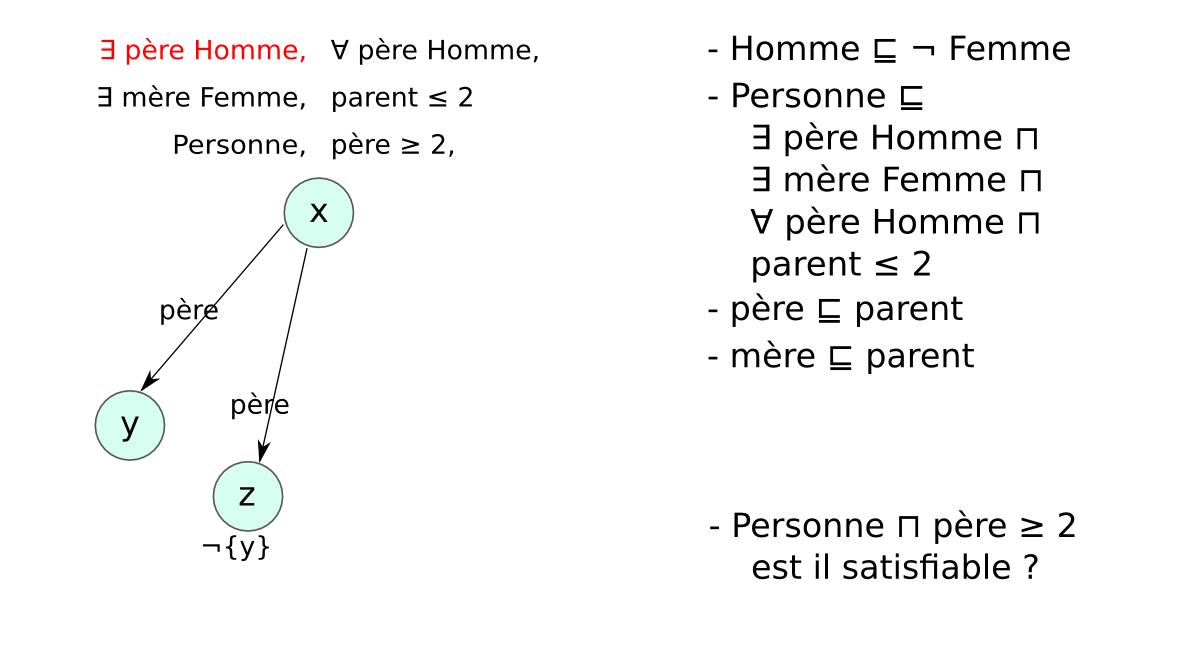
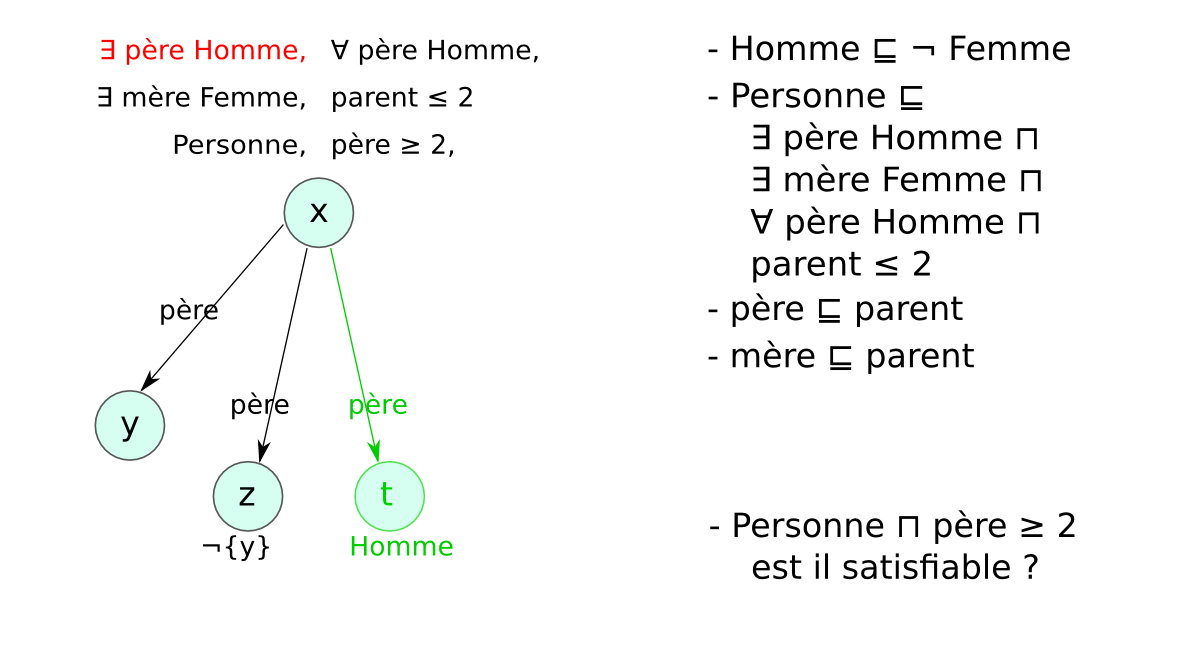
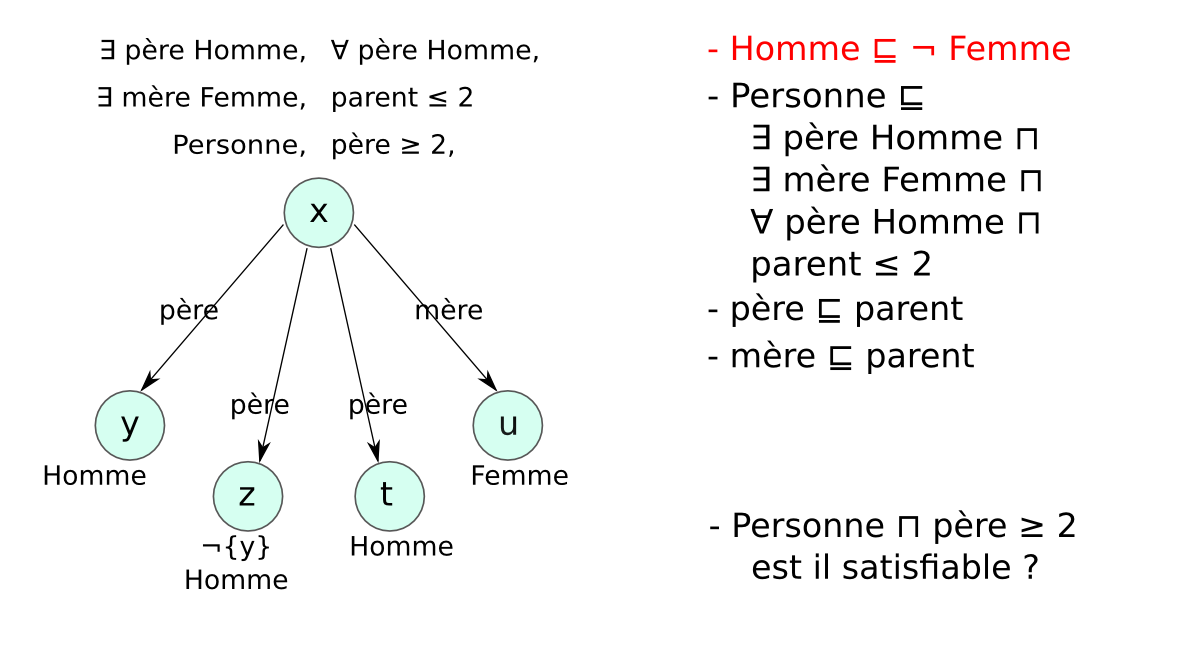
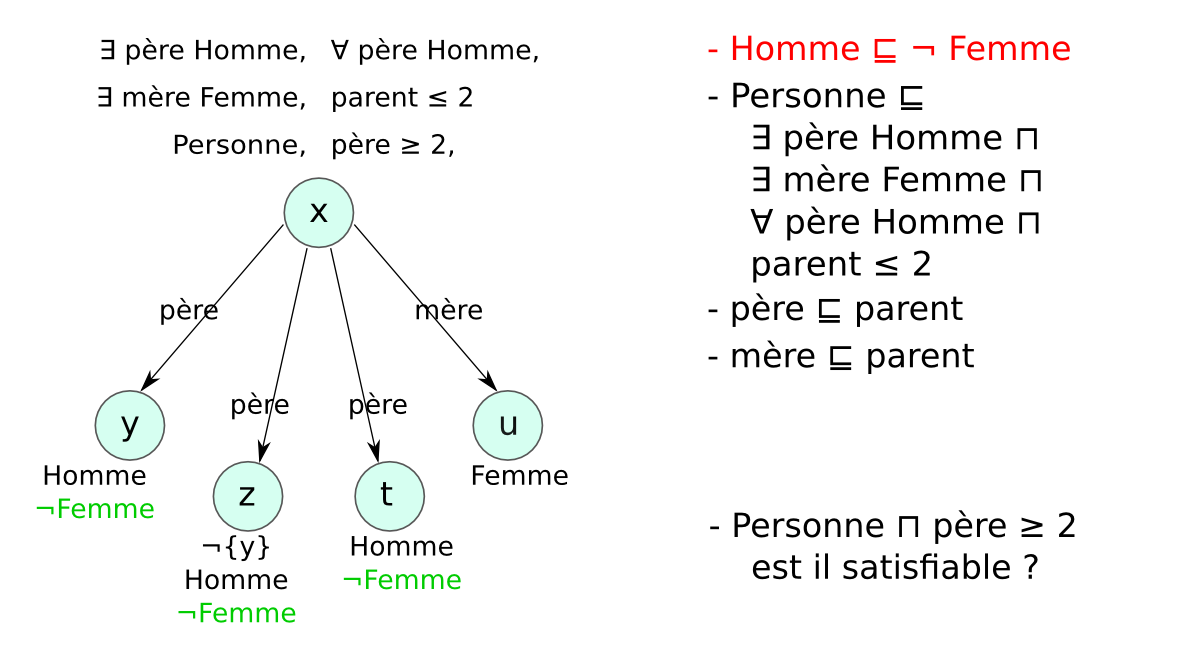
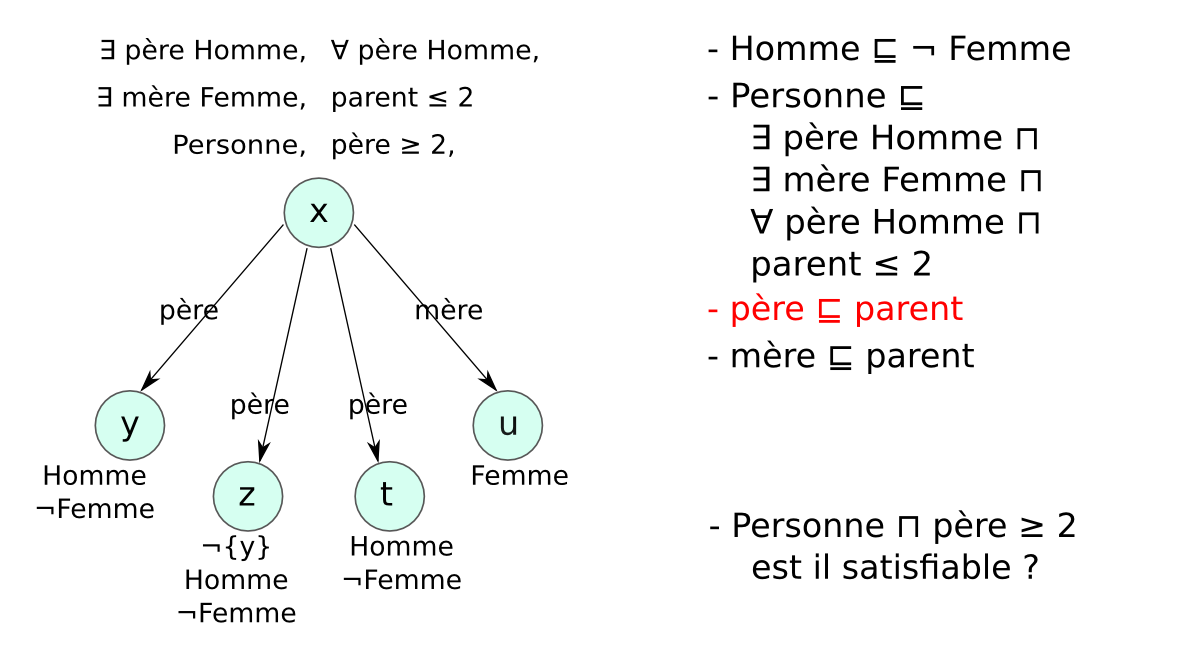
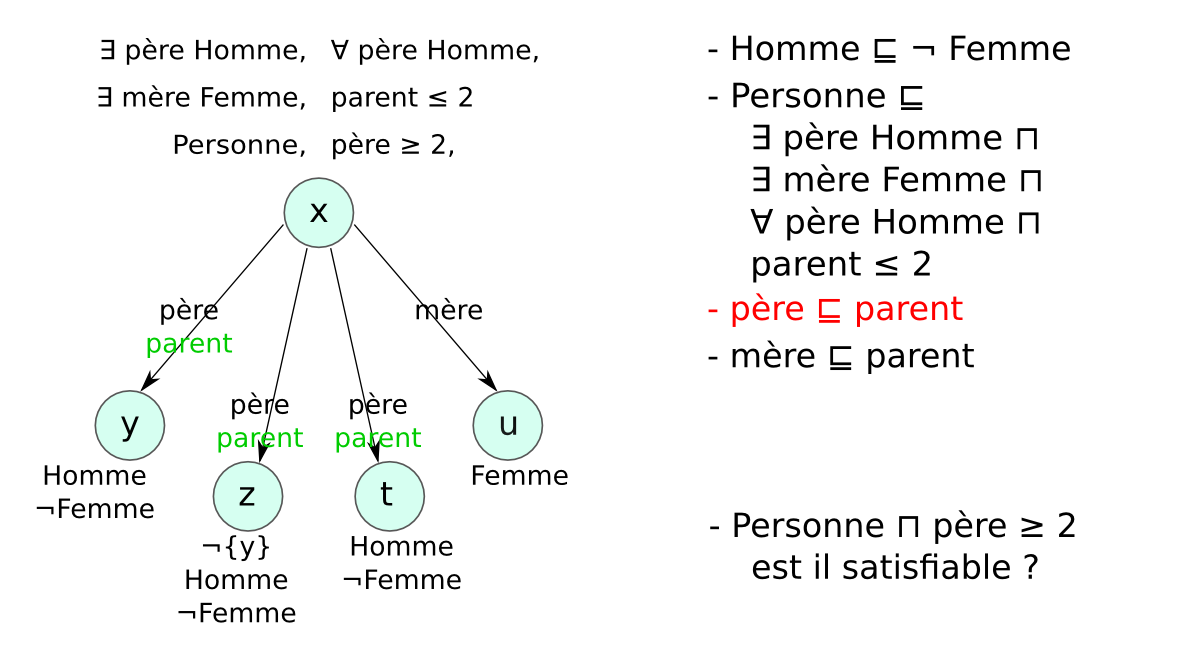
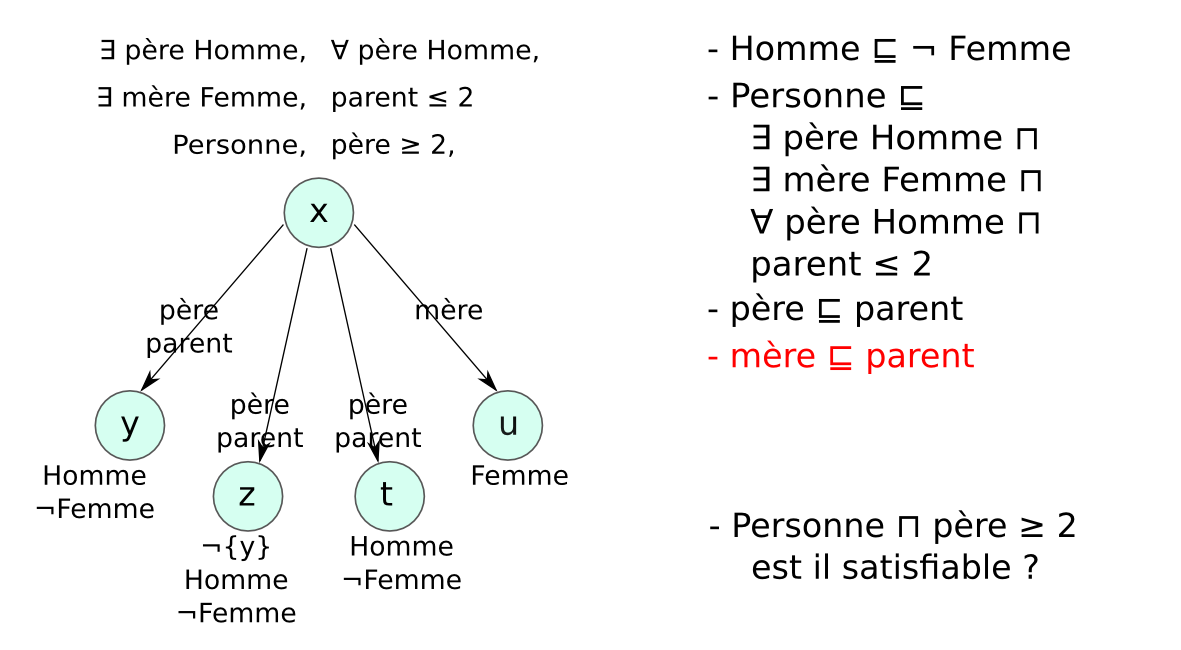
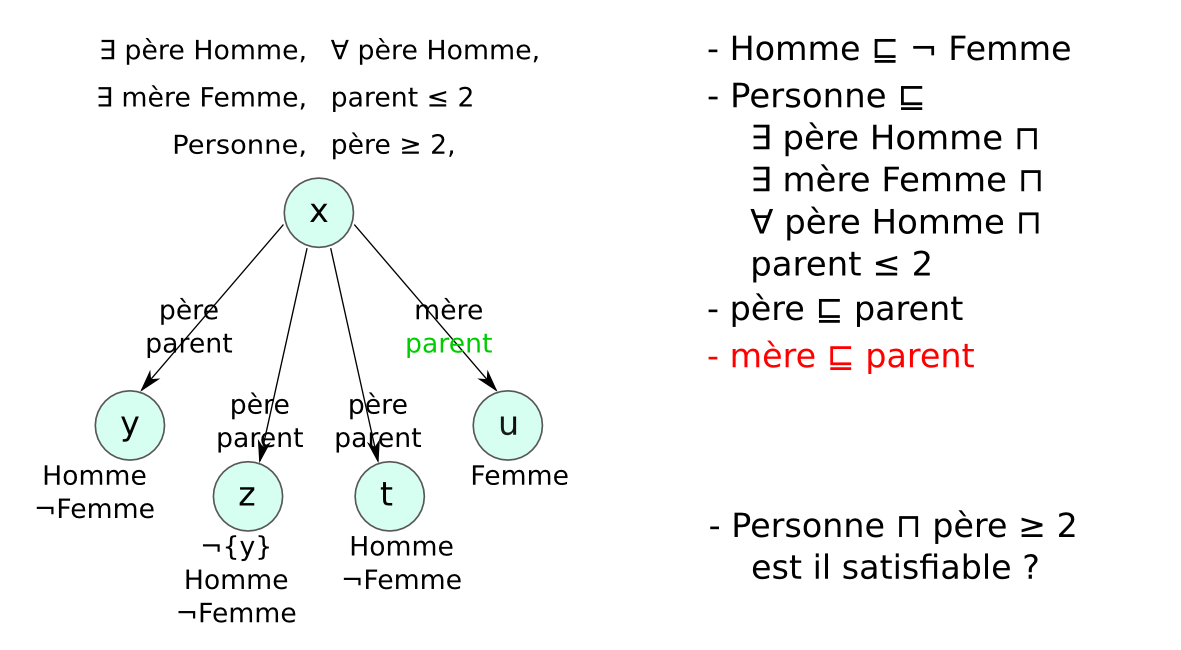
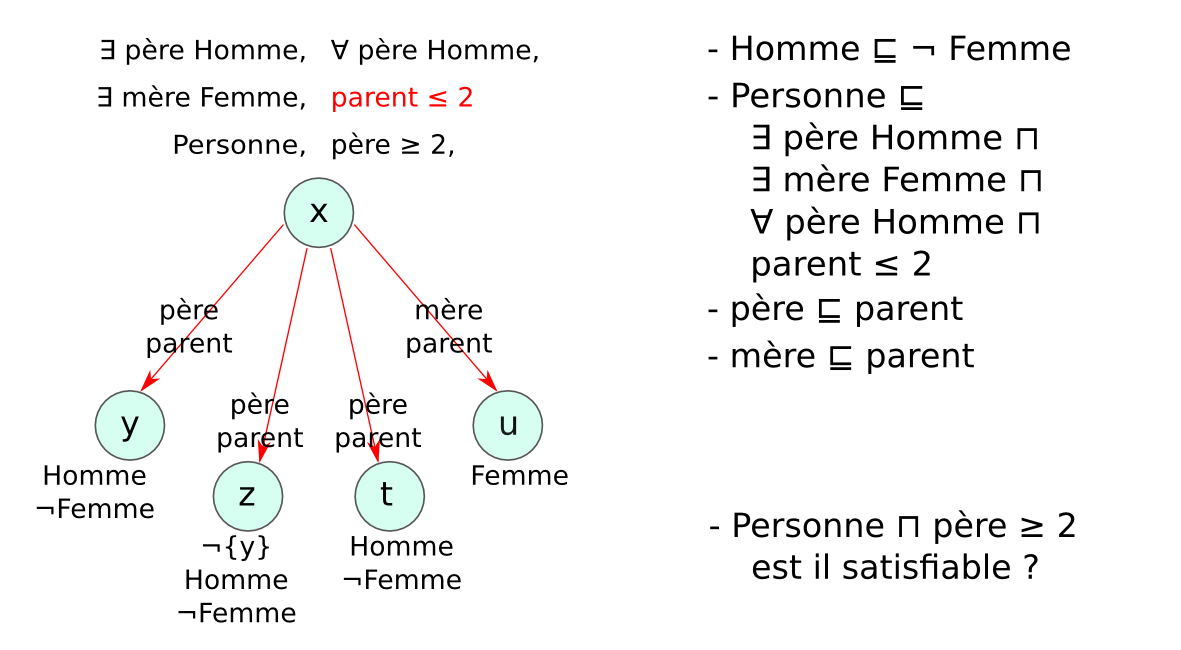
  • Problème des modèles infinis : exemple
    • Entier ⊑ (= 1 suivant Entier) ⊓ (≤ 1 suivant⁻)
    • {zero} ⊑ Entier ⊓ (= 0 suivant⁻)

Méta-modélisation§

  • En théorie : séparation stricte entre les individus, les concepts et les rôles
  • En pratique : pas d’ambiguïté syntaxique sur la nature d’un terme
  • Punning (calembour) : autorisation d’utiliser le même terme pour des éléments de nature différente
    • aucun lien sémantique entre eux
    • mais intérêt pragmatique
  • ⚠ pas très bien supporté par Protégé :-(

Annexe : Protégé§

Installation§

Téléchargement de Protégé (version ≥ 4)

Prise en main

Syntaxe de Protégé§

Protégé utilise une syntaxe alternative

  • inspirée de la syntaxe Manchester
  • n’utilisant que l’alphabet latin
  • donnes des phrases en pseudo-anglais → lisibilité

Concepts complexes : constructeurs ensemblistes§

Protégé LD
Thing ⊤
Nothing ⊥
C and D C ⊓ D
C or D C ⊔ D
not C ¬C
{a} {a}

Concepts complexes : restrictions§

Protégé LD
r some C ∃ r C
r only C ∀ r C
r exactly n C = n r C
r max n C ≤ n r C
r min n C ≥ n r C

Rôles complexes§

Protégé LD
inverse(r) r⁻
r o s r∘s

Axiomes dans Protégé-OWL§

Protégé offre des axiomes « de haut niveau » qui visent à

  • améliorer la lisibilité de la base de connaissance
  • optimiser le raisonnement
  • contraindre l’utilisation de certains constructeurs à certaines formes d’axiome selon les profils (e.g. Property Chain)

NB: ces axioms viennent en fait du langage OWL.

Sur les concepts§

Protégé LD
Equivalent class(C,D) C ⊑ D et D ⊑ C
Super class(C,D) C ⊑ D
Member(C,a) C(a)
Disjoint class(C,D) C ⊑ ¬D

Sur les rôles§

Protégé LD
Functional(r) ⊤ ⊑ (≤ 1 r)
Inverse functional(r) ⊤ ⊑ (≤ 1 r⁻)
Transitive(r) r ∘ r ⊑ r
Symmetric(r) r ⊑ r⁻
Asymmetric(r) r ⊑ ¬(r⁻)
Reflexive(r) ⊤ ⊑ (∃ r self)
Irreflexive(r) ⊤ ⊑ ¬(∃ r self)

Sur les rôles (suite)§

Protégé LD
Domain(r,C) ∃ r ⊑ C
Range(r,C) ∃ r⁻ ⊑ C
Equivalent property(r,p) r ⊑ p et p ⊑ r
Super property(r,p) r ⊑ p
Inverse property(r,p) r ⊑ p⁻ et p⁻ ⊑ r
Disjoint property(r,p) r ⊑ ¬p
Property chain(r,p,q...) p ∘ q ∘ ... ⊑ r