Logiques de descriptions§
| author: | Pierre-Antoine Champin |
|---|
Historique§
Logique§
- Logique des propositions (Boole)
- Logique des prédicats (Frege, ...)
- Calculabilité, complexité (Turing-Church)
- Incomplétude (Gödel)
Règles§
Clauses de Horn
Systèmes experts (PROLOG)
cretois(minos) . menteur(X) :- cretois(X) . ?- menteur(minos) yes ?- menteur(M) M=minos
Difficulté à maintenir de grosses bases de règles
Logiques « intuitives »§
- Réseaux sémantiques
- représentation graphique
Logiques « intuitives » (suite)§
Frames (Minsky)
approche « objet »
stéréotypes
valeurs par défaut
logique non monotone
(tous les oiseaux volent, les autruches ne volent pas)
Remise en ordre§
- graphes conceptuels (Sowa)
- représentation graphique formalisée
- logiques de descriptions
- représentation logique simplifiée
Logiques de description§
- Pas un langage, mais une famille de langage
- Formalisme de plus haut niveau que la LPO
- Compromis maîtrisé entre décidabilité et complexité
- Autres appellations :
- logiques descriptives
- logiques terminologiques
Syntaxe et sémantique§
Éléments de base§
L'univers du discours est constitué d'individus, appartenant à des concepts (ou classes), et reliés entre eux par des rôles (ou propriété).
| LD | LPO |
|---|---|
| Individu | Terme |
| Concept | Prédicat 1-aire |
| Rôle | Prédicat 2-aire |
Exemples§
| Concepts | Rôles | Individus |
|---|---|---|
| Homme | connait | john |
| Voiture | (a pour) père | jane |
| Rouge | mère | ab-123-cd |
| Menteur | enfant | |
| Ferrari | conduit |
Axiomes§
| Syntaxe | Appellation | Sémantique |
|---|---|---|
| C ⊑ D | subsomption de concepts | ∀ x, C(x) → D(x) |
| r ⊑ s | subsomption de rôles | ∀ x, y, r(x, y) → s(x, y) |
NB: l'équivalence peut s'exprimer par deux subsomptions symétriques : C ⊑ D et D ⊑ C
Axiomes : exemples§
- Crétois ⊑ Menteur
- ami ⊑ connait
Concepts complexes : constructeurs ensemblistes§
| Syntaxe | Appellation | Sémantique |
|---|---|---|
| ⊤ | concept universel (top) | Δ |
| ⊥ | concept absurde (bottom) | ∅ |
| ¬C | complément | { x | ¬C(x) } |
| C ⊔ D | union | { x | C(x) } ∪ { x | D(x) } |
| C ⊓ D | intersection | { x | C(x) } ∩ { x | D(x) } |
| {a} | extension | {a} |
Constructeurs ensemblistes : exemples§
- ¬Menteur
- Homme ⊔ Voiture
- Crétois ⊓ Menteur
- Voiture ⊓ (Rouge ⊔ ¬Ferrari)
- {john, paul, george, ringo}
Concepts complexes : restrictions§
| Syntaxe | Appellation | Sémantique |
|---|---|---|
| ∃ r C | qualificateur existentiel | { x | ∃ y, r(x, y) ∧ C(y) } |
| ∀ r C | qualificateur universel | { x | ∀ y, ¬r(x, y) ∨ C(y) } |
| = n r C | quantificateur | { x | #{y | r(x, y) ∧ C(y)} = n } |
| ≤ n r C | quantificateur (max) | { x | #{y | r(x, y) ∧ C(y)} ≤ n } |
| ≥ n r C | quantificateur (min) | { x | #{y | r(x, y) ∧ C(y)} ≥ n } |
NB : on omet généralement C lorsqu'il s'agit de ⊤ ; e.g.
∃ r , ∀ r , = 1 r ...
Restrictions : exemples§
- ∃ enfant
- ∀ conduit Ferrari
- (∃ conduit) ⊓ (∀ conduit Ferrari)
- = 2 conduit Ferrari
- ≥ 2 connait (Crétois ⊓ Menteur)
Rôles complexes§
| Syntaxe | Appellation | Sémantique |
|---|---|---|
| r⁻ | rôle inverse | { (x, y) | r(y, x) } |
| r∘s | rôle composé | { (x, y) | ∃ z, r(x, z) ∧ s(z, y) } |
| ¬r | complément | { (x, y) | ¬r(x, y) } |
Exemples§
- conduit⁻
- connait ∘ conduit
- connait ∘ connait
Axiomes complexes : exemples§
- ∃ conduit ⊑ Adulte
- ∃ conduit⁻ ⊑ Voiture
- Personne ⊑ Adulte ⊔ Enfant
- Personne ⊑ (= 1 père Homme) ⊓ (= 1 mère Femme)
- Personne ⊑ ¬Voiture
Décidabilité et complexité§
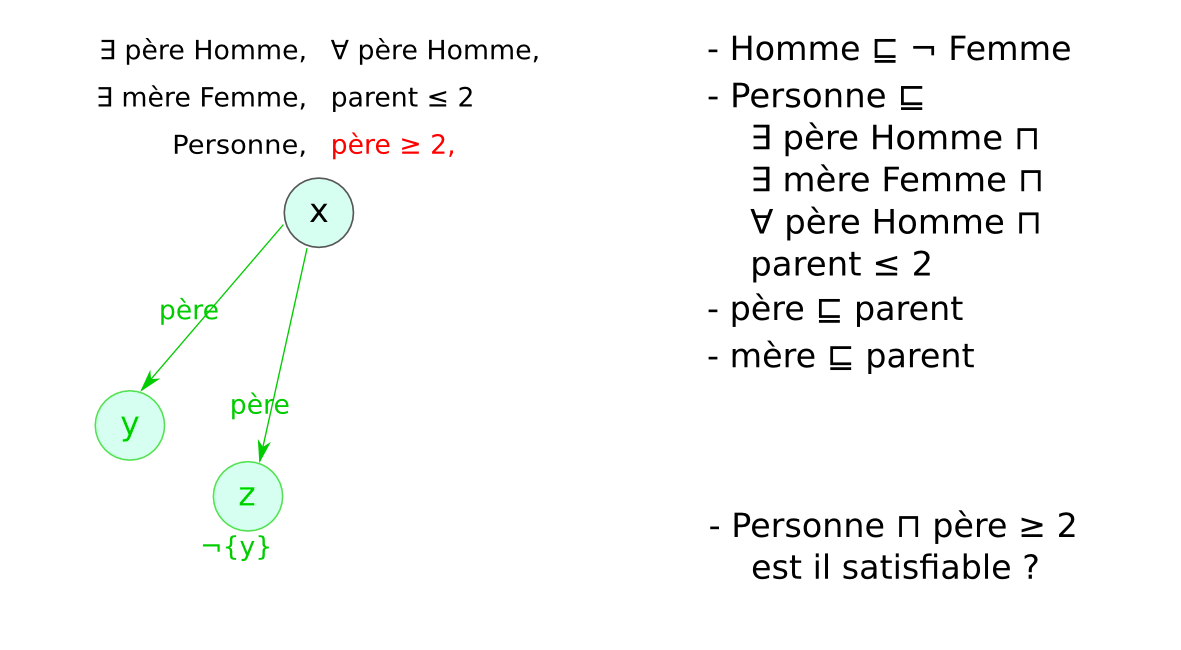
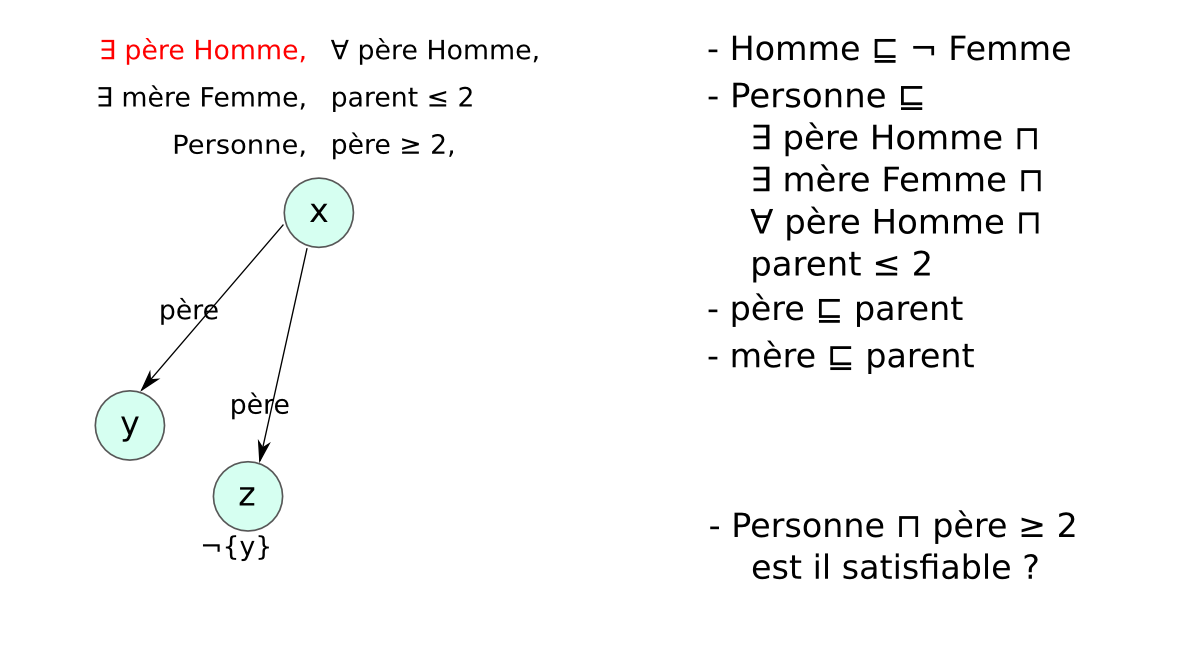
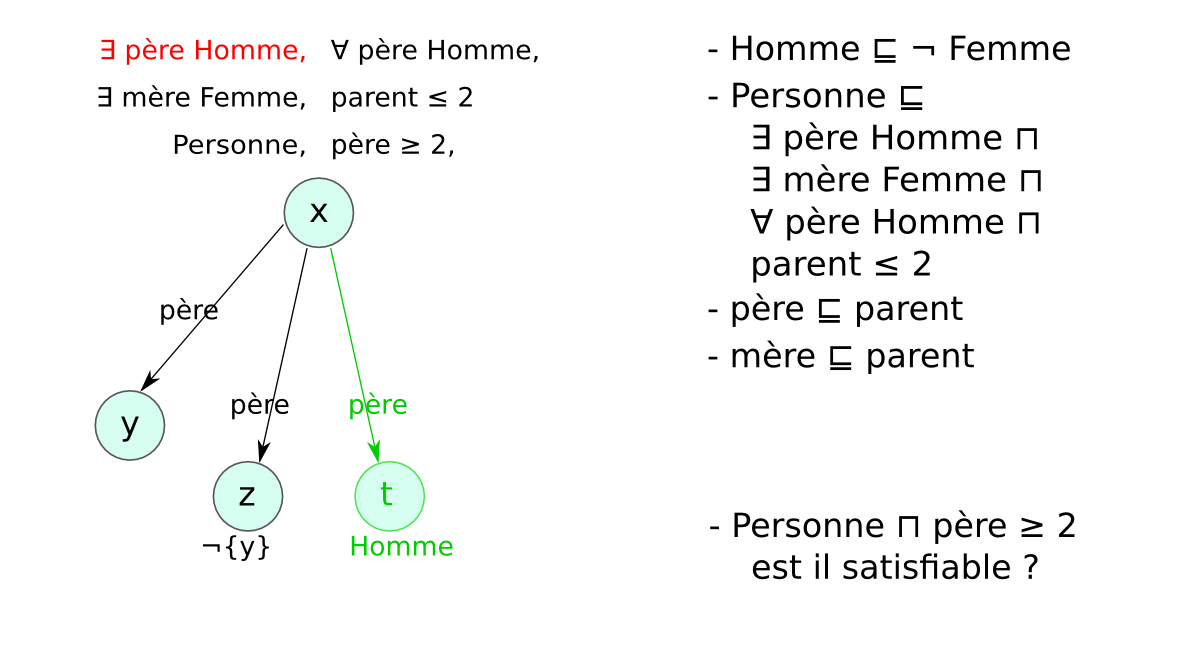
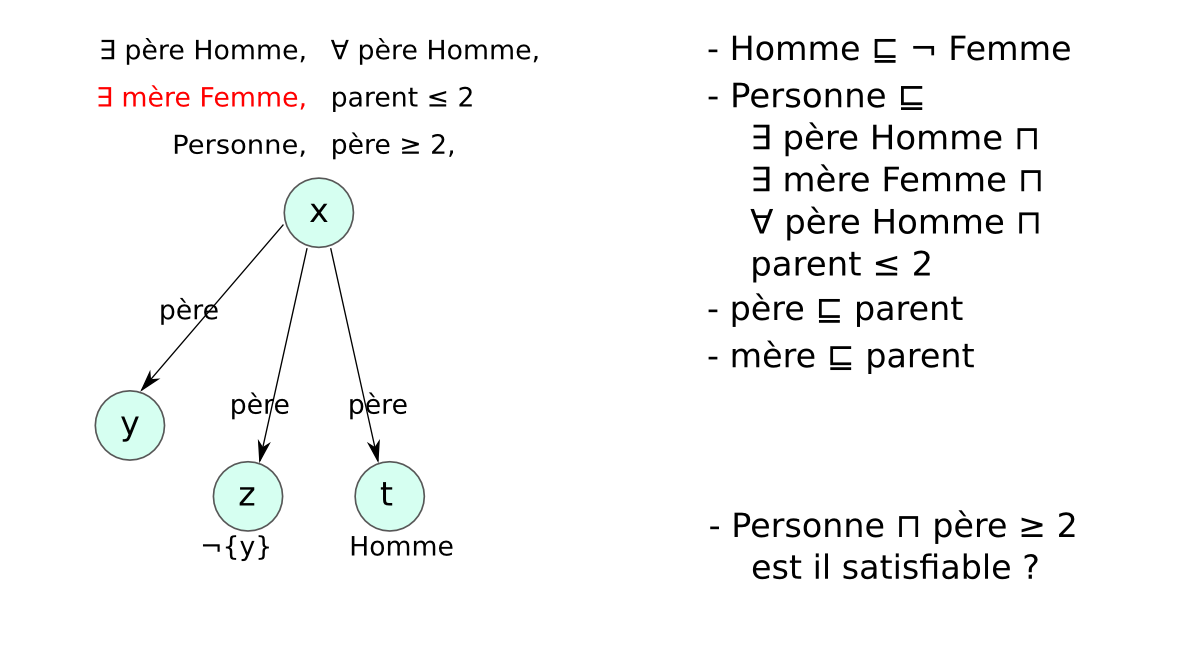
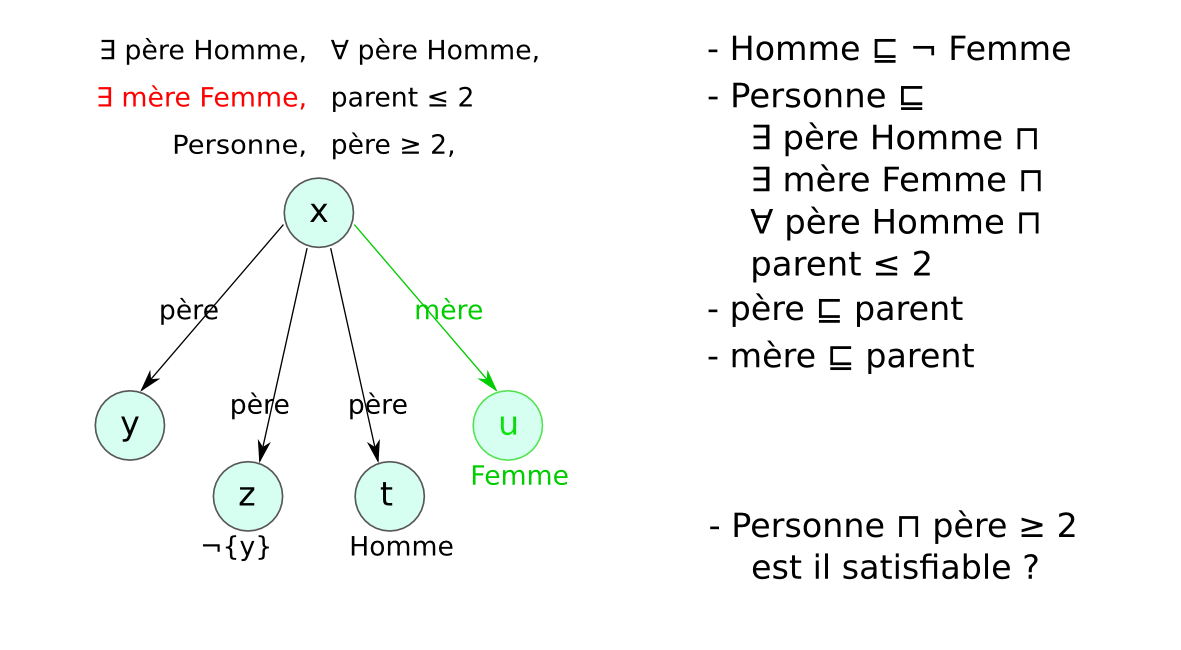
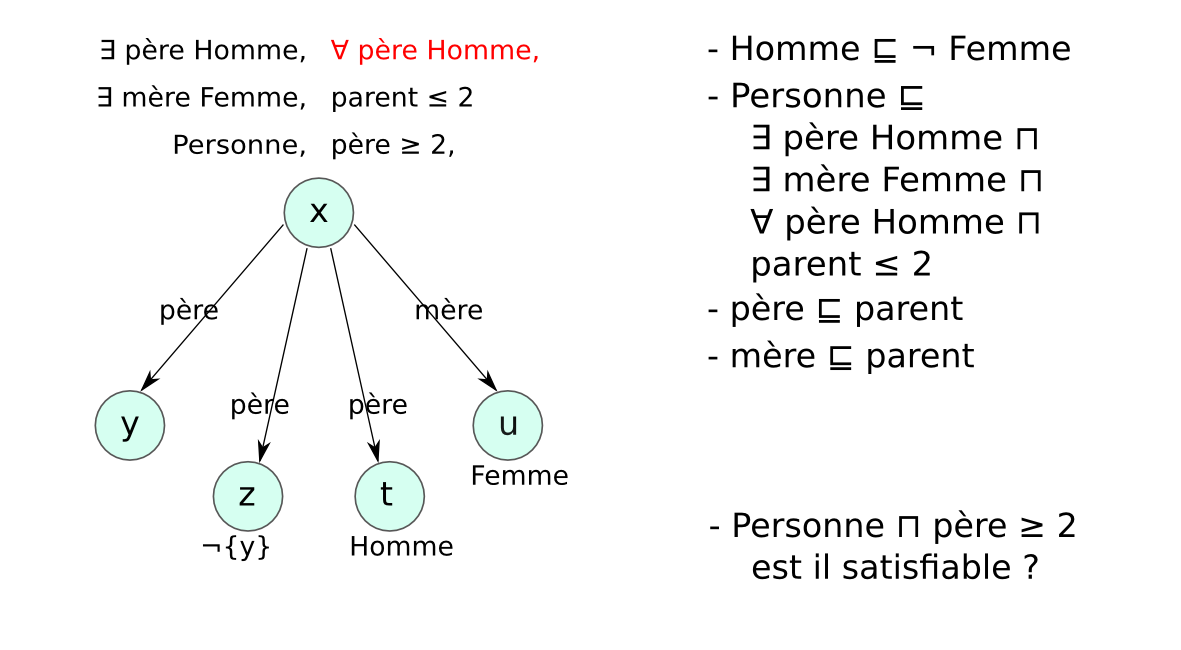
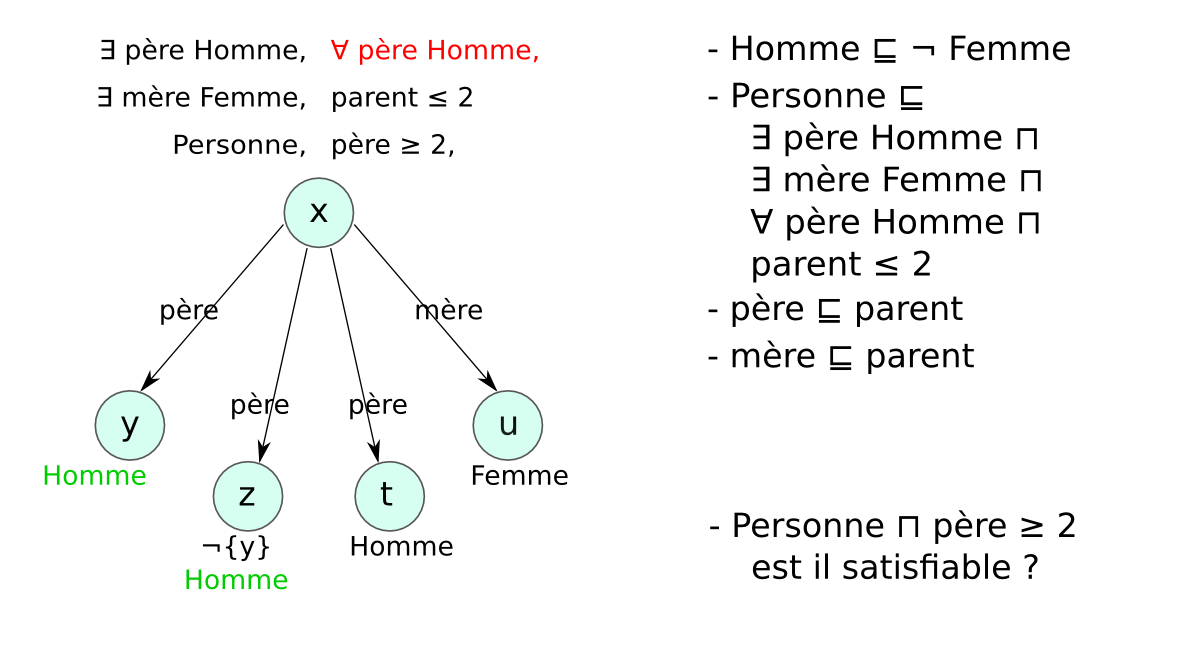
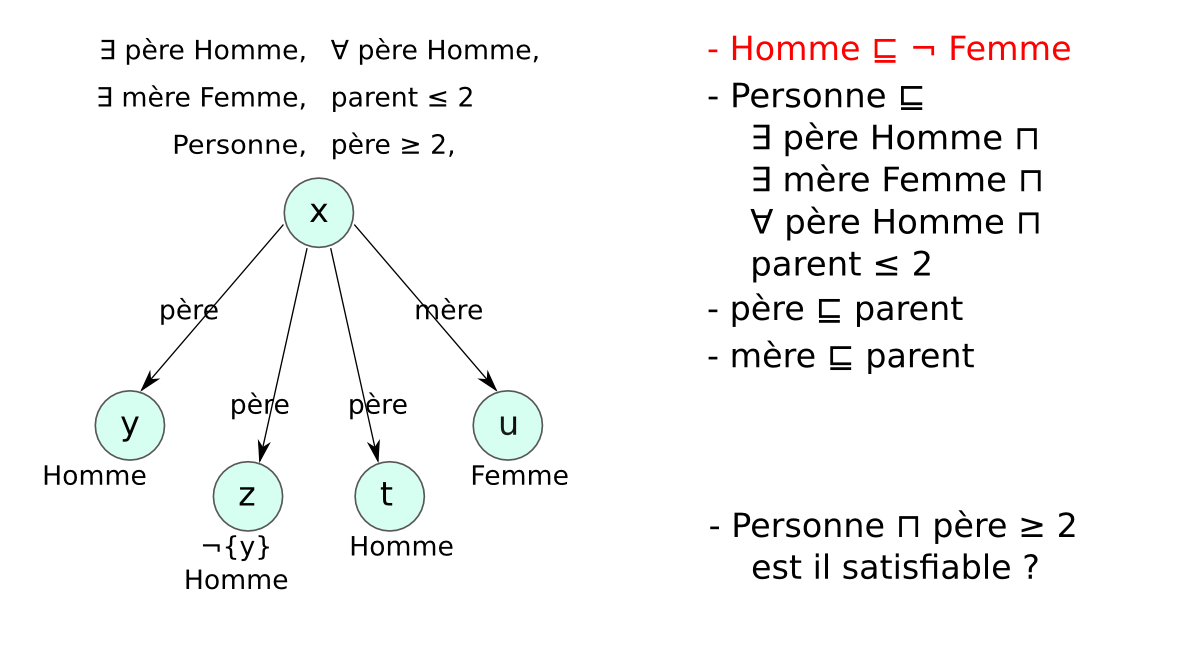
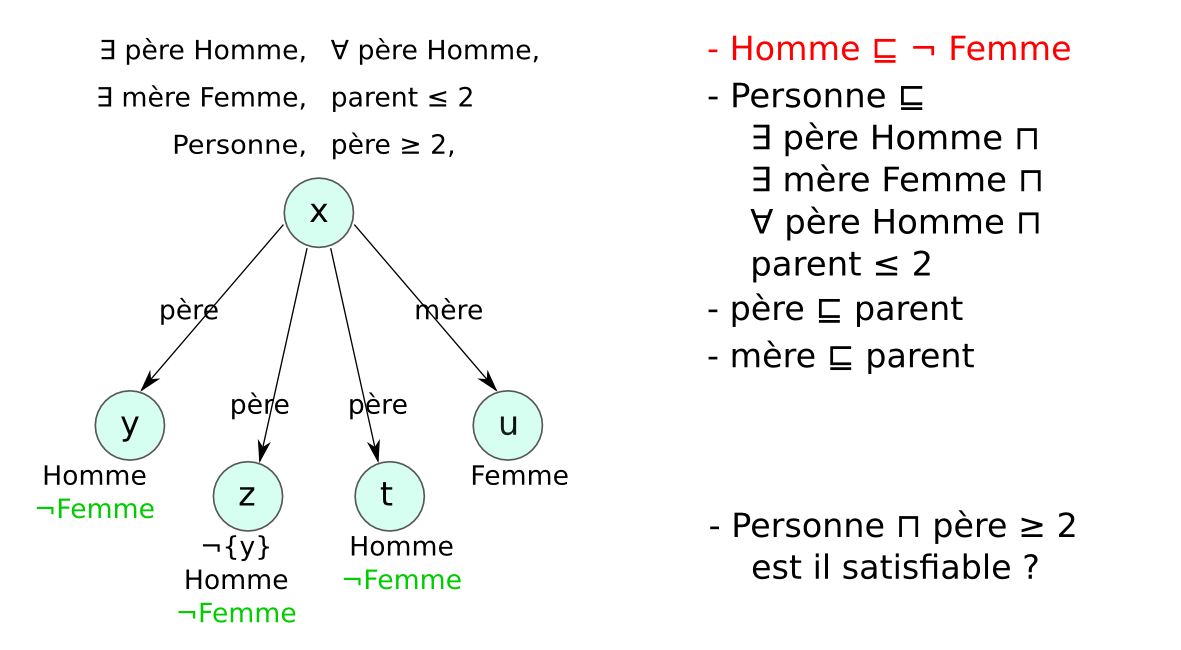
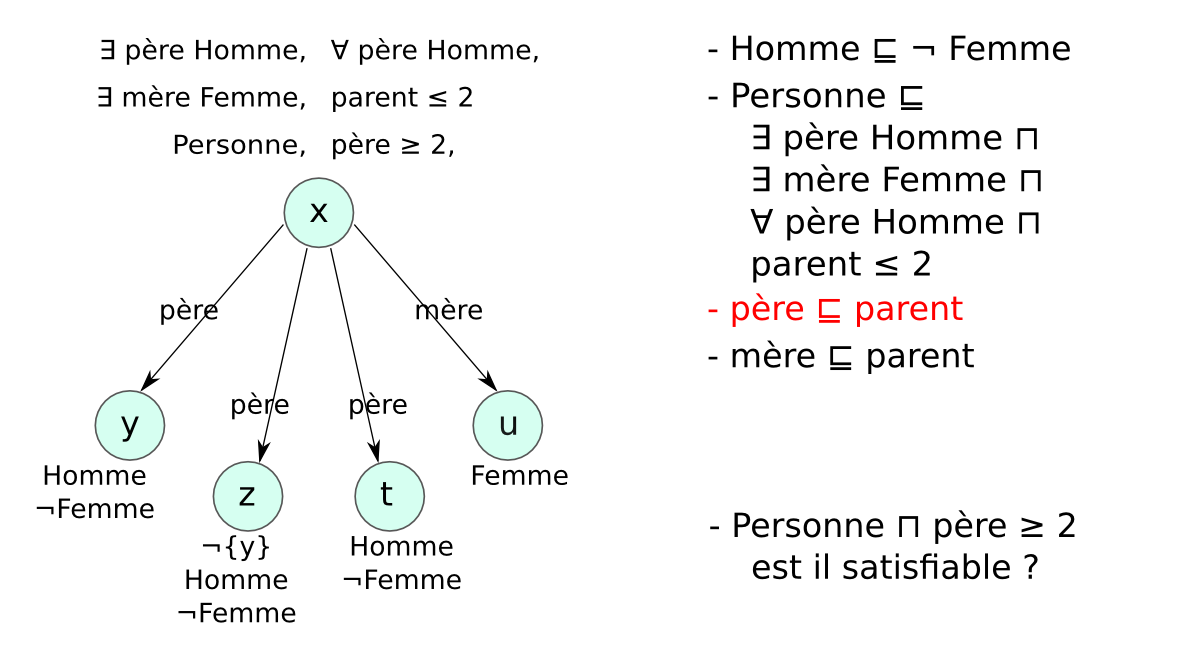
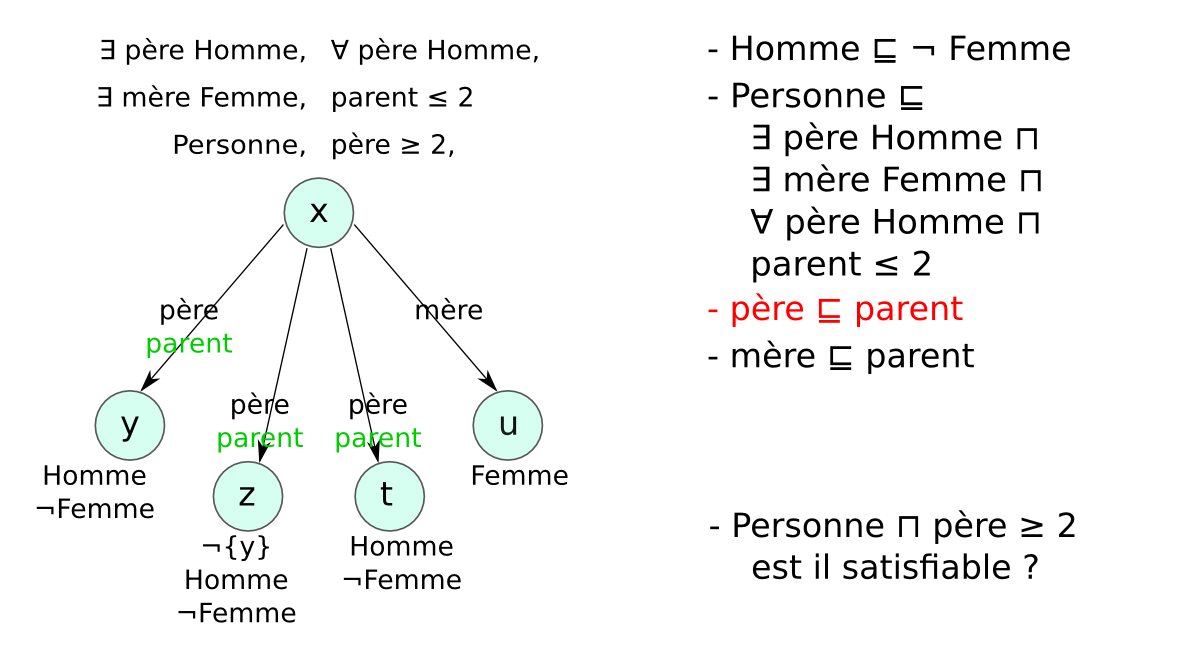
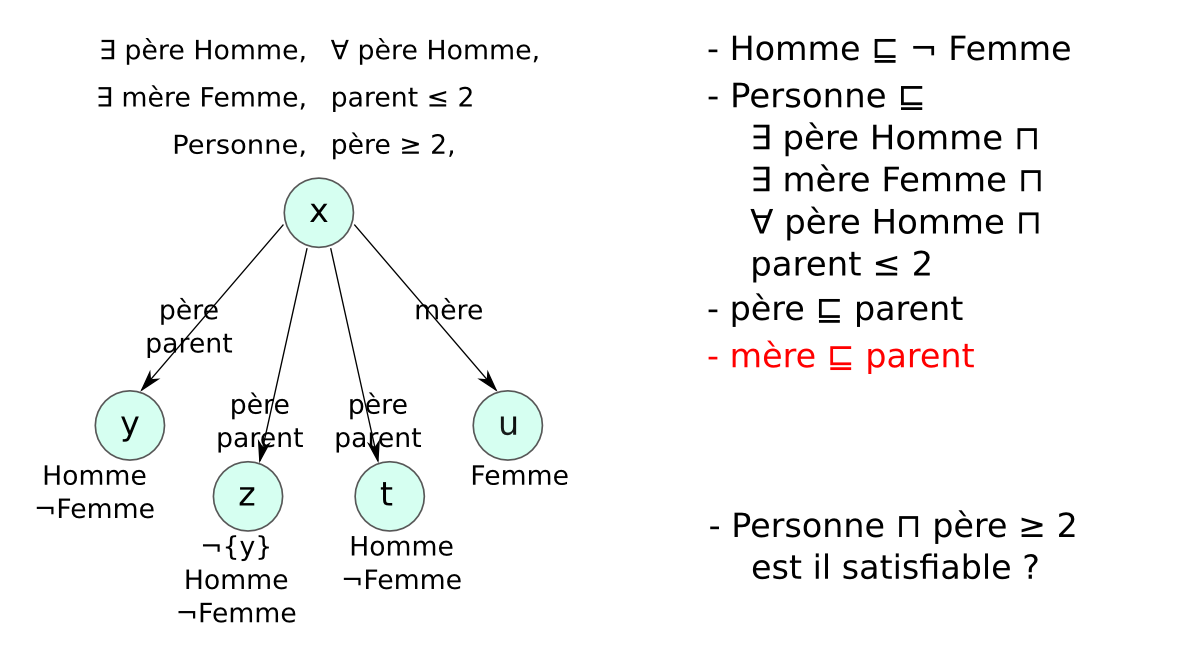
Chaque LD impose des contraintes sur :
- les axiomes autorisés,
- les constructeurs autorisés,
- la manière de les combiner,
afin de garantir que les mécanismes de raisonnement
- seront décidables,
- auront une complexité maximale.
→ compromis entre expressivité et complexité.
Raisonnement§
Rappels§
- Interprétation de F
- domaine du discours
- fonction d'interprétation
- Modèle
- axiomes → contraintes
- Implication
- F est satisfiable si elle a au moins un modèle
- F ⊧ G ssi tous les modèles de F sont des modèles de G
- ⇒ F ⊧ G ssi F ∧ ¬G est non satisfiable
Méthode des tableaux§
- Un tableau est un arbre, représentant une famille de modèles
- Application systématique de règles pour explorer tous les modèles possibles (non déterministe)
- Preuve par réfutation : concept non satisfiable
Exemple§
Enjeux§
- Décidable : dépend du type de LD choisie
- Correct/complet : ensemble de règles de transformation
- Complexe : optimiser l'ordre d'application des règles
- Problème des modèles infinis : exemple
- Entier ⊑ (= 1 suivant Entier) ⊓ (≤ 1 suivant⁻)
- {zero} ⊑ Entier ⊓ (= 0 suivant⁻)
Implémentations§
- Hermit
- http://hermit-reasoner.com/
- Pellet
- http://clarkparsia.com/pellet
- Racer
- http://www.racer-systems.com/
- FaCT
- http://www.cs.man.ac.uk/~horrocks/FaCT/
Méta-modélisation§
- En théorie : séparation stricte entre les individus, les concepts et les rôles
- En pratique : pas d'ambiguïté syntaxique sur la nature d'un terme
- Punning (calembour) : autorisation d'utiliser le même terme pour des éléments de nature différente
- aucun lien sémantique entre eux
- mais intérêt pragmatique
- ⚠ pas très bien supporté par Protégé :-(
Annexe : Protégé§
Installation§
Téléchargement de Protégé (version ≥ 4)
http://protege.stanford.edu/
Prise en main
http://protegewiki.stanford.edu/wiki/Protege4GettingStarted
Syntaxe de Protégé§
Protégé utilise une syntaxe alternative
- inspirée de la syntaxe Manchester
- n'utilisant que l'alphabet latin
- donnes des phrases en pseudo-anglais → lisibilité
Concepts complexes : constructeurs ensemblistes§
| Protégé | LD |
|---|---|
| Thing | ⊤ |
| Nothing | ⊥ |
| C and D | C ⊓ D |
| C or D | C ⊔ D |
| not C | ¬C |
| {a} | {a} |
Concepts complexes : restrictions§
| Protégé | LD |
|---|---|
| r some C | ∃ r C |
| r only C | ∀ r C |
| r exactly n C | = n r C |
| r max n C | ≤ n r C |
| r min n C | ≥ n r C |
Rôles complexes§
| Protégé | LD |
|---|---|
| inverse(r) | r⁻ |
| r o s | r∘s |
Axiomes dans Protégé-OWL§
Protégé offre des axiomes « de haut niveau » qui visent à
- améliorer la lisibilité de la base de connaissance
- optimiser le raisonnement
- contraindre l'utilisation de certains constructeurs à certaines formes d'axiome selon les profils (e.g. Property Chain)
NB: ces axioms viennent en fait du langage OWL.
Sur les concepts§
| Protégé | LD |
|---|---|
| Equivalent class(C,D) | C ⊑ D et D ⊑ C |
| Super class(C,D) | C ⊑ D |
| Member(C,a) | C(a) |
| Disjoint class(C,D) | C ⊑ ¬D |
Sur les rôles§
| Protégé | LD |
|---|---|
| Functional(r) | ⊤ ⊑ (≤ 1 r) |
| Inverse functional(r) | ⊤ ⊑ (≤ 1 r⁻) |
| Transitive(r) | r ∘ r ⊑ r |
| Symmetric(r) | r ⊑ r⁻ |
| Asymmetric(r) | r ⊑ ¬(r⁻) |
| Reflexive(r) | ⊤ ⊑ (∃ r self) |
| Irreflexive(r) | ⊤ ⊑ ¬(∃ r self) |
Sur les rôles (suite)§
| Protégé | LD |
|---|---|
| Domain(r,C) | ∃ r ⊑ C |
| Range(r,C) | ∃ r⁻ ⊑ C |
| Equivalent property(r,p) | r ⊑ p et p ⊑ r |
| Super property(r,p) | r ⊑ p |
| Inverse property(r,p) | r ⊑ p⁻ et p⁻ ⊑ r |
| Disjoint property(r,p) | r ⊑ ¬p |
| Property chain(r,p,q...) | p ∘ q ∘ ... ⊑ r |