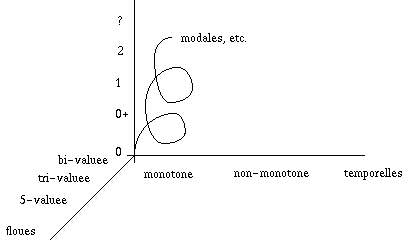
La première idée pour "représenter" des connaissances est de se rapprocher d'un système "logique", c'est-à-dire capable de dire le Vrai et le Faux en fonction d'axiomes de bases et de "théorèmes" de dérivation. On retrouve bien sûr la "patte" des mathématiciens logiciens, en particuliers des logiciens grecs, dont le plus célèbre est sans aucun doute Aristote (voir l'encyclopédie Yahoo par exemple).
Pour démontrer qu'une expression est un théorème, nous avons une procédure
(développer l'arbre) infaillible, qui répond en 2n/2, n étant
la longueur de la chaîne, donc en temps fini.
Par contre, pour démontrer qu'une expression est un non-théorème, il nous faut
"tricher". Dans les deux exemples ci-dessus, nous avons fait de l'arithmétique,
que faudrait-il faire sur un autre exemple?
Si, pour prouver qu'une expression est un théorème, il "suffit" d'explorer l'ensemble des thèorèmes qui peuvent être générés, il n'est pas possible de faire la même chose pour un non-théorème. En pratique, on utiliserait le raisonnement par l'absurde, en posant que l'expression est un théorème, et en cherchant s'il est possible de trouver les théorèmes qui ont été utilisés avec les règles pour produire ce nouveau théorème.
Supposons pupueuu comme expression à décider théorème ou non. Ce théorème peut provenir de l'application de la règle R1 ou R2. La règle R1 ajoute un u au début et à la fin du théorème dérivé. Je ne peux pas enlever un u en début de mot, il ne peut donc y avoir aucun théorème ayant produit celui-ci avec la règle R1. La règle R2 ajoute un u avant et après un e dans un théorème pour en produire un autre. Il est possible de trouver une expression d'origine qui aurait pu produire celle-ci par la règle indiquée : pupeu. Est-ce que cette expression est un théorème ? On peut démontrer facilement que cette expression n'est pas dérivable d'une expression quelconque par la règle R1 ou la règle R2. Il ne peut donc pas s'agir d'un théorème.
Donc les notions de "être un théorème" et de "être un non-théorème" ne sont pas symétriques. Notre système "peu" est semi-décidable : nous avons une procédure qui répond "oui" en temps fini, mais pas de procédure pour répondre "non".
EXERCICE 2_2
Ce que vous avez manipulé dans l'exercice 2 3 n'est pas un système formel
: le symbole "2" ne fait pas partie de l'alphabet. Ce que nous manipulons est
l'interprétation du système formel. "1+1+1=3", dans l'interprétation,
est vrai, bien que ce soit un non-théorème.
Une interprétation d'un S.F. n'est
en général pas équivalente au S.F., c'est-à-dire que les notions
de "être un théorème" et "être un non-théorème" d'une part, et de "être vrai"
et "être faux" d'autre part, peuvent ne pas se recouvrir.
Cependant, il ne faut pas rejeter l'interprétation : souvenez-vous, si vous
avez étudié un peu de Géométrie, la première fois qu'on vous a demandé "démontrer
que le triangle ABC est isocèle". Vous avez soigneusement mesuré les deux cotés,
et vous avez dit : "Oui, les deux cotés sont égaux". Et l'enseignant vous a
répondu : "NON! Ce n'est pas parce que c'est vrai sur la figure que c'est un
théorème". Mais vous n'avez pas pour autant cessé de faire des figures pour
résoudre les problèmes, parce qu'elles guident le raisonnement. Nous
y reviendrons.
Considérons un système formel quelconque, et l'ensemble (qui peut être infini) des expressions qu'on peut engendrer dans ce système en appliquant le procédé de formation des expressions. Nous pouvons partitionner cet ensemble en : les expressions qui sont des théorèmes, et celles qui sont des non-théorèmes.
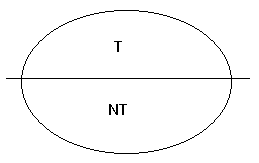
Nous pouvons également partitionner cet ensemble en : ce qu'une procédure peut
démontrer en temps fini, et ce qu'elle ne peut pas :
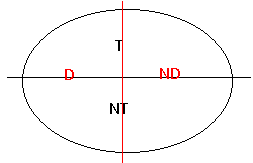
Si la partie ND (Non Démontrable) est vide, le système est dit décidable.
Si la partie TND est vide, il est semi-décidable. Si aucune partie n'est vide,
il est indécidable.
Nous pouvons par ailleurs partitionner l'ensemble en : les expressions dont
l'interprétation est "vrai", et celles dont l'interprétation est "faux" :
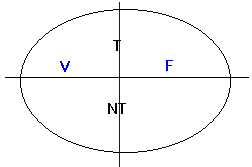
Si la partie TF n'est pas vide, nous dirons que notre interprétation est sans
intérêt (en effet, il ne sert à rien de dire ce qui est vrai si on peut
le démontrer à coup sûr). On montre en revanche que la partie
NTV n'est, en général, pas vide.
Lorsqu'une proposition "manifestement vraie" ne peut être démontrée, on est
donc en droit de se demander dans laquelle de ces zones on se trouve. Un cas
célèbre était la conjecture de Fermat, qui a tenu les mathématiciens en échec
pendant trois siècles : il n'existe pas d'entiers positifs x, y et z, et d'entier
n supérieur à 2, tels que x^n+y^n=z^n (^ représente l'opérateur
"puissance").
| alphabet | distance.<.2km distance.<.300km aller.à.pied prendre.le.train prendre.l'avion avoir.le.téléphone aller.à.l'agence téléphoner.à.l'agence acheter.un.billet durée.>.2.jours être.fonctionnaire ( ) non (négation) ^ (et, ou conjonction) -> (implique) |
| procédé de formation des expressions |
expression <= symbole expression <= ( expression ) expression <= non expression expression <= expression1 ^ expression2 expression <= expression1 -> expression2 |
| axiomes | R1 : distance.<.2km -> aller.à.pied
R2 : ((non distance.<.2km) ^ distance.<.300km) ->
prendre.le.train
R3 : (non distance.<.300km) -> prendre.l'avion
R4 : (acheter.un.billet ^ avoir.le.téléphone) ->
téléphoner.à.l'agence
R5 : (acheter.un.billet ^ (non avoir.le.téléphone)) ->
aller.à.l'agence
R6 : prendre.l'avion -> acheter.un.billet
R7 : (durée.>.2.jours ^ être.fonctionnaire) ->
(non prendre.l'avion)
F1 : (non distance.<.300km)
F2 : avoir.le.téléphone
|
| règle de dérivation |
Si A est un théorème, et si A -> B est un théorème, alors B est un théorèmeCette règle est connue sous le nom de "modus ponens" |
ça marche
tant que ça marche
ça ne marche pas
boucle sur les Ri
boucle sur les Fj
si Ri est de la forme "Fj -> Fk"
ajouter Fk à la BdF
ça marche
finsi
finboucle
finboucle
fintant
|
ça ne marche pas R1 et F1 : rien R1 et F2 : rien R2 et F1 : rien R2 et F2 : rien R3 et F1 : F3 (prendre.l'avion) et ça marche R3 et F2 : rien R3 et F3 : rien ... R6 et F3 : F4 (acheter.un.billet) et ça marche ... R7 et F4 : rien ça ne marche pas R1 et F1 : rien R1 et F2 : rien R1 et F3 : rien R1 et F4 : rien ... R4 et F4 et F2 : F5 (téléphoner.à.l'agence) Est-ce que cette règle va vraiment être tirée? (Exercice 2_4 : Réponse)
Pour que cette règle soit tirée, il aurait fallu une règle de dérivation du type ci-dessous :
| règle de dérivation |
Si A est un théorème, et si B est un théorème, alors A ^ B est un théorème |
La distinction entre "et" et "^" n'est pas un snobisme, pas plus que celle que nous faisons entre "si...alors..." et "->" . Corrigeons :
ça marche
tant que ça marche
ça ne marche pas
boucle sur les Ri
boucle sur les Fj
si Ri est de la forme "Fj -> Fk"
ajouter Fk à la BdF
ça marche
sinon
boucle sur les Fm
si Ri est de la forme "Fj ^ Fm ->..."
ajouter Fp = (Fj ^ Fm) à la BdF
ça marche
finsi
finboucle
finsi
finboucle
finboucle
fintant
|
ça ne marche pas
modus ponens avec R3 et F1 : F3 (prendre.l'avion) et ça marche
modus ponens avec R6 et F3 : F4 (acheter.un.billet) et ça marche
ça ne marche pas
règle du "et" avec F4 et F2 : F5 (acheter.un.billet ^ avoir.le.téléphone)
et ça marche
ça ne marche pas
modus ponens avec R4 et F5 : F6 (téléphoner.à.l'agence) et ça marche
ça ne marche pas
arrêt
NON! C'est
vrai en Logique, mais pas en Informatique ! Notre programme va continuer à produire
des faits.
Exercice 2_5 : Montrez-le et expliquez pourquoi (réponse)
Notre programme ne donne pas la solution en temps fini, car il boucle. Pour éviter cela, nous marquons les Fj au fur et à mesure que nous les utilisons :
ça marche
tant que ça marche
ça ne marche pas
boucle sur les Ri
boucle sur les Fj non marqués
si Ri est de la forme "Fj -> Fk"
ajouter Fk à la BdF
marquer Fj
ça marche
sinon
boucle sur les Fm
si Ri est de la forme "Fj ^ Fm ->..."
ajouter Fp = (Fj ^ Fm) à la BdF
marquer Fj
ça marche
finsi
finboucle
finsi
finboucle
finboucle
fintant
|
| axiomes | R1 : distance.<.2km -> aller.à.pied
R2 : ((non distance.<.2km) ^ distance.<.300km) ->
prendre.le.train
R3 : (non distance.<.300km) -> prendre.l'avion
R4 : (acheter.un.billet ^ avoir.le.téléphone) ->
téléphoner.à.l'agence
R5 : (acheter.un.billet ^ (non avoir.le.téléphone)) ->
aller.à.l'agence
R6 : prendre.l'avion -> acheter.un.billet
R7 : (durée.>.2.jours ^ être.fonctionnaire) ->
(non prendre.l'avion)
F1 : (non distance.<.300km)
F2 : avoir.le.téléphone
F3 : durée.>.2.jours
F4 : être.fonctionnaire
|
modus ponens avec R3 et F1 : F5 (prendre.l'avion) !! modus ponens avec R6 et F5 : F6 (acheter.un.billet) règle du "et" avec F3 et F4 : F7 (durée.>.2.jours ^ être.fonctionnaire) règle du "et" avec F4 et F2 : F5 (acheter.un.billet ^ avoir.le.téléphone) modus ponens avec R4 et F5 : F6 (téléphoner.à.l'agence) modus ponens avec R7 et F7 : F8 (non prendre.l'avion) !!L'"expert" va s'insurger : notre système a déduit, d'une part, qu'il fallait prendre l'avion (F5), et d'autre part qu'il ne fallait pas (F8).
Q : pourquoi F5? R : modus ponens avec R3 et F1 Q : pourquoi F8 ? R : modus ponens avec R7 et F7 Q : pourquoi F7? R : règle du "et" avec F3 et F4Nous savons à présent que l'erreur provient d'une contradiction entre R3 et R7, que nous montrons à l'expert. Comment corriger? En supprimant R3, et en le remplaçant par les bons axiomes, ceux qui traitent tous les cas. Où placer les nouveaux axiomes? N'importe où.
Dorénavant, nous appellerons "règles" les axiomes de type Ri,
c'est-à-dire les axiomes qui contiennent "->", et qui forment la BdC.
C'est regrettable, car cela entretient une confusion avec les règles de dérivation,
mais c'est l'usage.
Une règle a une partie gauche (LHS) et une partie droite (RHS).
La partie gauche est une conjonction de prémisses, c'est-à-dire que les prémisses
sont reliées par des ^. La partie droite est une conjonction de conséquents.
(F1^F2^...^Fn) -> (F'1^F'2^...^F'm) est une règle.
En Prolog, la partie droite est à gauche, et il n'y a qu'un seul conséquent.
F'1 : F1^F2^...^Fn
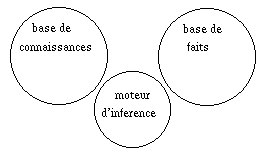
F1 : distance.=.500km F2 : avoir.le.téléphoneIl ne se passe rien. Le système ne sait pas, à partir du symbole distance.=.500km , affirmer
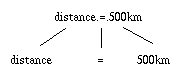
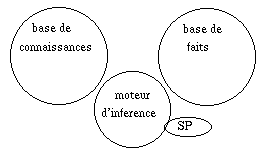
Nous avons quitté le Calcul des Propositions, ou Logique d'ordre 0, pour une
Logique que nous appellerons "0+", dans laquelle apparaissent des "trucs valuables",
des constantes, et des prédicats. Le prix à payer est de programmer la sémantique
des prédicats, c'est-à-dire d'écrire un programme capable, par exemple, de remplacer
"distance = 500km" par "non distance < 300km". D'où la verrue sur le nez
de Mickey.
| axiomes | R1 : distance.destination < 2km -> aller.à.pied.destination
R1a : distance.agence < 2km -> aller.à.pied.agence
R2 : ((non distance.destination < 2km)
^ distance.destination < 300km) ->
prendre.le.train.destination
R2a : ((non distance.agence < 2km)
^ distance.agence < 300km) -> prendre.le.train.agence
...
F1 : distance.destination = 500km
F2 : distance.agence = 1,5km
F3 : non avoir.le.téléphone
|
Mais supposons maintenant que je veuille travailler sur n objets : je
ne peux pas "n-pliquer" mon système. Il faut que je puisse écrire :
R1 : quelle que soit la destination, distance(destination) < 2km -> aller.à.pied(destination)
destination devient alors une variable, et j'ai introduit
d'autre part "quelle que soit", qu'on appelle le quantificateur universel,
noté 
.
Je suis à présent en Calcul des Prédicats du Premier Ordre, ou "Logique d'Ordre
1". Mon moteur d'inférence va se compliquer, puisqu'il va devoir chercher, non
plus à faire coller un "F" avec la partie gauche d'un "R", mais chercher quelles
valeurs des variables permettent cet appariement.
(En savoir plus cliquer ici)
R (x y
z (xRy) ^ (yRz) -> (xRz)) -> transitive
(R)) Supposons à présent que j'écrive :
fenêtre.ouverte ^ courant.d'air -> fermer.la.fenêtre
"fermer.la.fenêtre" est un théorème, qui doit s'entendre : "il faut fermer la
fenêtre". Mais ce qui m'interesserait, c'est qu'un robot domotique dispose de
telles connaissances, et qu'il aille effectivement fermer la fenêtre avec ses
petites mains. "fermer.la.fenêtre" devient alors une action. Mais
si mon robot ferme la fenêtre, il y aura contradiction entre l'état du monde
et sa Base de Faits, qui contiendra encore "fenêtre.ouverte". Donc, il faut
compléter :
fenêtre.ouverte ^ courant.d'air -> fermer.la.fenêtre ^ non fenêtre.ouverte
Ce qui revient à écrire : A ^ ... -> non A ^ ...
Or toute la Logique repose sur l'interdiction d'une telle formule !
Nous créons donc (dans les années 70), les Logiques non monotones, dans lesquelles
cela n'est plus interdit. (non monotone, par analogie avec l'Analyse : le nombre
de théorèmes n'est plus une fonction non-décroissante du temps).
Nous gagnons en puissance d'expression,
mais nous perdons quelque chose de très important : la certitude de terminer
en temps fini. En effet, la même situation peut se reproduire (quelqu'un ré-ouvre
la fenêtre), et il faudra appliquer à nouveau la même règle aux mêmes faits
; nous ne pouvons donc plus marquer comme au 2.2.2., et donc le système peut
boucler.
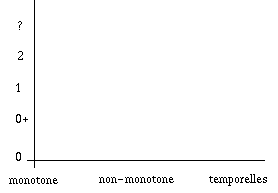
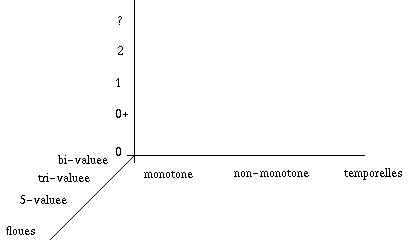
On remarquera que cette notion de monotonie/non-monotonie est indépendante de
l'Ordre de la Logique considérée :
X
A, A -> sait(X A).