Quad-Optimized Low-Discrepancy Sequences

Abstract

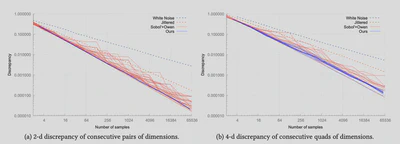
The convergence of Monte Carlo integration is given by the unifor- mity of samples as well as the regularity of the integrand. Despite much effort dedicated to producing excellent, extremely uniform, sampling patterns, the Sobol’ sampler remains unchallenged in production rendering systems. This is not only due to its reason- able quality, but also because it allows for integration in (almost) arbitrary dimension, with arbitrary sample count, while actually producing sequences thus allowing for progressive rendering, with fast sample generation and small memory footprint. We improve over Sobol’ sequences in terms of sample uniformity in consecutive 2-d and 4-d projections, while providing similar practical benefits – sequences, high dimensionality, speed and compactness. We base our contribution on a base-3 Sobol’ construction, involving a search over irreducible polynomials and generator matrices, that produce (1, 4)-sequences or (2,4)-sequences in all consecutive quadruplets of dimensions, and (0, 2)-sequence in all consecutive pairs of di- mensions. We provide these polynomials and matrices that may be used as a replacement of Joe & Kuo’s widely used ones, with computational overhead, for moderate-dimensional problems.