


La topologie algébrique (anciennement appelée topologie combinatoire) est une branche des mathématiques cherchant à étudier les espaces topologiques en leur associant un objet algébrique (groupe, espace vectoriel, …) dont les propriétés servent à déterminer un certain nombre d’invariants caractérisant la topologie de l’espace initial. Deux outils ont été beaucoup utilisés afin de réaliser cette étude : le groupe fondamental ou plus généralement la théorie de l’homotopie, et le groupe d’homologie ou groupe de co-homologie.
Le problème de la théorie de l’homotopie est que les groupes d’homotopie sont difficilement exploitables de manière simple. Une difficulté importante provient de la représentation de ces groupes qui est réalisée par un ensemble de mots et des relations sur ces mots. De ce fait, savoir si deux groupes sont isomorphes revient à résoudre le problème du mot1. Or, ce problème a été montré indécidable [Nov55] ce qui implique que le problème général de savoir si deux groupes fondamentaux sont isomorphes l’est également2. Pour s’affranchir de ce problème, nous nous intéressons donc ici à la théorie de l’homologie dans laquelle les représentations des groupes et les algorithmes de calcul peuvent être envisagés. Pour cette raison, nous n’étudions donc pas du tout par la suite le groupe fondamental mais uniquement les groupes d’homologie et les notions associées.
Dans nos travaux, nous nous intéressons aux partitions d’espaces en cellules comme les complexes simpliciaux ou les complexes cellulaires. Intuitivement, nous souhaitons représenter un sous-espace de ℝn de manière combinatoire c’est-à-dire en «oubliant» la forme. Il existe différentes manières de faire selon les propriétés des objets représentés (par exemple orientables ou non, simpliciaux ou cellulaires…), mais dans tous les cas, il est important de pouvoir contrôler la validité des objets représentés. C’est pour cette raison que la partie la plus importante dans la définition de modèles combinatoires concerne leurs contraintes de cohérence. Ce sont elles qui vont garantir que l’objet combinatoire correspond bien à son équivalent topologique. Elles peuvent également autoriser la vérification algorithmique qu’un objet donné est valide ou non. Dans ce cadre, nous nous sommes plus particulièrement aux cartes combinatoires et cartes généralisées, deux modèles permettant de représenter des partitions cellulaires nD, et autorisant un accès efficace aux cellules et aux relations entre celles-ci.
L’objectif de ce chapitre est de centraliser les principales notions autour des cartes combinatoires et généralisées. La plupart de ces notions sont issues des deux papiers de références [Lie91, Lie94] ainsi que du chapitre de livre [LFB07] ; les notions préliminaires sont souvent issues des livres [Spa66, Cro78, Mun84, Hat02] ; certains éléments proviennent de la lecture des thèses [Elt94, Lan95, Ala05, Pel06, Fav09, Dup09]. Certaines notions concernant le dual et les cartes ouvertes sont «re-découvertes» dans ce chapitre : soit car les notions originales ne correspondent pas exactement à celles utilisées ; soit car elles manquaient d’explications, d’illustrations ou de preuves. J’espère que ce chapitre pourra servir de référence pour un lecteur cherchant des explications précises sur les cartes, en regroupant en un même endroit les principales notions portant sur les cartes combinatoires et généralisées.
Ce chapitre est organisé de la manière suivante. Nous présentons Section 2.1 les notions de base de topologie algébrique, les notations utilisées dans ce mémoire, et quatre modèles topologiques classiques qui sont les complexes simpliciaux, les complexes cellulaires, les complexes simpliciaux abstraits et les complexes cellulaires abstraits. Nous introduisons Section 2.2 des structures combinatoires permettant de représenter ces modèles, ou certaines sous-classes, et décrivant directement les relations entre les éléments : les ensembles semi-simpliciaux qui sont une sous-classe des complexes simpliciaux ; les cartes combinatoires, en rappelant l’historique de leur définition en 2D, et les cartes généralisées, qui permettent de représenter des sous-classes de complexes cellulaires orientables pour les cartes combinatoires, et quelconques pour les cartes généralisées. Nous détaillons également les cartes combinatoires ouvertes, une extension des cartes pouvant représenter des complexes ouverts. La Section 2.3 détaille le lien entre les cartes et les ensembles semi-simpliciaux, ce qui permet de transposer des définitions basées sur les complexes simpliciaux vers les complexes cellulaires, comme par exemple le calcul de la caractéristique d’Euler-Poincaré.
Nous commençons par présenter quelques notions de base de topologie algébrique qui seront utiles dans la suite de ce mémoire.
Soit un ensemble E, une famille d’ensembles sur E (ou famille de sous-ensembles de E) est un ensemble de sous-ensembles de E. P(E) est l’ensemble des parties de E . C’est une famille d’ensembles sur E définie par P(E)={X ⊆ E}. Une partition P de E est une famille d’ensembles sur E telle que les éléments de P sont deux à deux disjoints et forment un recouvrement de E (cf. Def. 1).
Le couple (X,τ) est appelé espace topologique. Les éléments de X sont appelés les points, et les éléments de τ sont appelés les ouverts de la topologie. Un sous-ensemble de X est dit fermé si son complémentaire dans X est ouvert. Chaque élément de τ peut être ouvert, fermé, les deux à la fois, ou encore ni ouvert ni fermé. Par définition, ∅ et X sont toujours des ouverts et des fermés. Soit X un ensemble d’éléments, la topologie discrète sur X est la topologie (X,P(X)). De façon intuitive, c’est la topologie dans laquelle chaque point est «isolé». En effet, dans cette topologie, chaque point de X est à la fois ouvert et fermé. Une notion fondamentale en topologie est la notion de voisinage. Soit x ∈ X. V ⊆ X est un voisinage de x dans la topologie (X,τ) si il existe un ouvert inclus dans V contenant x. Le voisinage d’un point n’est jamais vide car X est un voisinage de tout point de X. Un espace topologique est dit séparé, ou espace de Hausdorff, si pour deux points distincts x et y quelconques, il existe un voisinage de x et un voisinage de y disjoints.
Bn est la boule unité nD : c’est l’ensemble des points x de ℝn tel que ||x|| ≤ 1 (avec si x=(x1,…,xn), ||x||=√x12+… xn2). La boule unité ouverte nD h(B)n est l’ensemble des points x de ℝn tel que ||x|| < 1. La demi-boule unité consiste à restreindre une coordonnée (la première dans ce qui suit) aux nombres positifs ou nuls. B1/2n = {x=(x1,…,xn) | ||x|| ≤ 1 et x1 ≥ 0}, et enfin la demi-boule unité ouverte3 est h(B1/2)n = {x=(x1,…,xn) | ||x|| < 1 et x1 > 0}. Sn−1 est la sphère unité nD : c’est l’ensemble des points x de ℝn tel que ||x|| = 1.
Par exemple Bn est une variété fermée, dont le bord est Sn−1, tandis que h(B)n est une variété ouverte, donc sans bord.
Une variété topologique nD est dite orientable s’il est possible de définir une direction «gauche» et «droite» globalement en tout point de la variété. Elle est dite non-orientable sinon. Deux exemples de 2-variétés non orientables sont présentés Fig. 2.1 : le ruban de Möbius à la Fig. 2.1.1, et la bouteille de Klein à la Fig. 2.1.1.
Après cette introduction aux notions topologiques de base, nous introduisons maintenant les notations et outils mathématiques que nous utilisons par la suite.
Soit E un ensemble non vide. Soit f une fonction de E dans E. f est une permutation sur E si c’est une bijection de E dans E. f est une involution sur E si c’est une bijection de E dans E telle que f=f−1, ce qui est équivalent à f ∘ f = IdE (une involution est donc une permutation particulière ; de ce fait, lorsque nous considérerons un ensemble de permutations, il pourra contenir des involutions). Soit e ∈ E, e est un point fixe de f si f(e)=e. Soit X ⊆ E, nous notons f(X)={f(x)|x ∈ X}. IdE est la fonction identité de E dans E .
Une relation d’ordre R pour un ensemble E est une relation binaire réflexive (x R x) transitive (x R y et y R z ⇒ x R z) et antisymétrique (x R y et y R x ⇒ x=y). Si pour tout couple d’éléments x,y dans E2, x et y sont comparables par R, la relation d’ordre est dite totale. Sinon elle est dite partielle.
Soit Φ={f1,…,fk} un ensemble de permutations sur un même ensemble E, et e ∈ E. Nous utilisons parfois la notation anglaise e f1 … fk pour fk(…(f1(e))). ⟨Φ⟩ est le groupe de permutations engendré par Φ. C’est l’ensemble des permutations qu’il est possible d’obtenir de Φ par application de la composition et de l’inverse. Ce groupe de permutations permet de définir la notion d’orbite d’un élément de E.
L’orbite d’un élément est l’ensemble des éléments de E qu’il est possible d’atteindre par application, à partir de e, de n’importe quelle suite de fi et fi−1. Étant donnée un ensemble de permutations Φ, nous notons z(⟨Φ⟩) le nombre d’orbites distinctes d’éléments de E, c’est-à-dire |{⟨Φ⟩(e)|e∈ E}| (cf. Section 2.2.3 pour des exemples d’orbites).
Un complexe simplicial [Spa66, Ago76, PBCF93, Hat02] peut être vu de manière constructive comme un espace topologique obtenu en collant entre eux des simplexes.
Un simplexe s de dimension n est un n-polyèdre5 formé par l’enveloppe convexe d’un ensemble P de n+1 points de ℝn affinement indépendants. Un sommet est un 0-simplexe, un segment un 1-simplexe, un triangle un 2-simplexe et un tétraèdre un 3-simplexe. Un n-simplexe est homéomorphe à la boule Bn. L’enveloppe convexe de n’importe quel sous-ensemble non vide de P est une face de s (donc une face est elle-même un simplexe). Un simplexe f est une coface de s si s est une face de f. Deux simplexes sont incidents si l’un est une face de l’autre, et deux i-simplexes s1 et s2 sont adjacents s’il existe un simplexe qui soit une face de s1 et une face de s2.
Par définition des simplexes comme enveloppe convexe de points affinement indépendants, un simplexe a nécessairement une géométrie linéaire (c-à-d chaque 1-simplexe est un segment de droite), et ne peut pas avoir de dégénérescence6. De plus, la définition d’un complexe simplicial interdit la présence de multi-incidence (c-à-d le cas de deux i-simplexes ayant pour intersection plus d’un simplexe. En effet, dans ce cas, l’intersection n’est pas une face des deux simplexes).
La Fig. 2.2 montre un exemple et un contre-exemple de complexe simplicial. Pour la Fig. 2.1.2, le complexe est composée de cinq sommets numérotés de 1 à 5, de six 1-simplexes et de deux 2-simplexes (donc le complexe contient en tout 13 simplexes). Il est facile de vérifier sur cet exemple que l’intersection de n’importe quel couple de simplexes est un simplexe ou est vide. Par contre, l’ensemble présenté Fig. 2.1.2 n’est pas un complexe simplicial car l’intersection des deux triangles n’est pas une face commune.
[a][b]
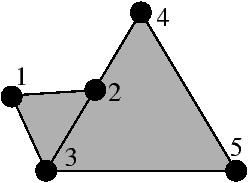
Figure 2.2: Un exemple (a) et un contre-exemple (b) de complexe simplicial. (a) L’ensemble contenant les deux 2-simplexes de sommets {a,b,c} et {a,b,d}, le 1-simplexe de sommets {b,e}, et toutes leurs faces est un complexe simplicial contenant cinq sommets, six 1-simplexes et deux 2-simplexes. (b) L’ensemble contenant les deux 2-simplexes et toutes leurs faces n’est pas un complexe simplicial car l’intersection des deux 2-simplexes de sommets {1,2,3} et {3,4,5} est l’arête de sommets {2,3} qui n’est pas une face du simplexe de sommets {3,4,5}.
La Def. 10 de pseudo-variétés7 permet de vérifier de manière combinatoire si un complexe simplicial représente une variété [Sti80].
Mais cette notion de pseudo-variété n’est pas équivalente à la notion de variété. Considérons l’exemple de la Fig. 2.3. C’est un ensemble de triangles formant une surface homémorphe à la sphère S2, dans lequel deux sommets de la surface sont identifiés. Ce complexe simplicial est une pseudo-variété (car chaque 1-simplexe est bien la face d’au plus deux 2-simplexes), mais n’est pas une variété car le voisinage du point résultat de l’identification n’est pas homéomorphe à la boule ouverte h(B2) ni à la demi-boule ouverte h(B1/2)2.
Les complexes simpliciaux ont été étendus pour pouvoir utiliser des éléments de base plus généraux que les simplexes : ce sont les CW-complexes (appelés parfois complexes cellulaires) défini par [Whi49]. Il existe de nombreux travaux autour des CW-complexes et leur étude sort du cadre de ce travail. Nous introduisons simplement ici les notions intuitives. De manière informelle, un CW-complexe est obtenu en collant entre elles des cellules de base qui sont homéomorphes à des boules Bn, de telle sorte que le collage respecte des propriétés de continuité. Plus précisément, un CW-complexe est un espace de Hausdorff X, avec une décomposition de X en cellules, et une fonction continue entre chaque n-cellule et Bn qui doit vérifier des propriétés supplémentaires. Il faut noter que cette définition des CW-complexes rend difficile la mise en œuvre de structure de données pour les manipuler de par la présence de la fonction continue et de ses propriétés. La Def. 10 de pseudo-variété est étendue au CW-complexes en remplaçant les simplexes par des cellules.
Un complexe simplicial abstrait (CSA) correspond à l’information purement combinatoire qu’il est possible d’extraire d’un complexe simplicial.
Chaque élément A de K est un simplexe. Un sous-ensemble de A étant une face de A, cette définition peut se reformuler en disant que chaque face de chaque simplexe appartient au complexe. La dimension d’une face A est |A|−1. La dimension du complexe est la plus grande dimension d’un simplexe de K. Un simplexe est dit principal s’il n’est la face d’aucun simplexe du complexe.
À tout complexe simplicial abstrait peut être associé un complexe simplicial. Ce complexe simplicial est appelée la réalisation géométrique du complexe simplicial abstrait. Il faut noter que cette réalisation géométrique est unique à isomorphisme près. Lors de l’association de la géométrie à un complexe simplicial abstrait, il faut vérifier que les contraintes géométriques du complexe simplicial sont satisfaites. De manière réciproque, à chaque complexe simplicial peut être associé un complexe simplicial abstrait. Il suffit d’énumérer tous les simplexes par leurs ensembles de sommets pour construire le complexe simplicial abstrait correspondant.
Prenons comme exemple le complexe simplicial abstrait {{a,b,c},{a,b,d},{b,e}, {a,b},{a,c},{b,c},{a,d},{b,d},{a},{b},{c},{d},{e}}. Les trois premiers éléments de cet ensemble sont les simplexes principaux. L’ensemble des sommets est {a,b,c,d,e}. {a,b} est une face de dimension 1 de {a,b,c}, et la dimension du complexe est 2. Le complexe simplicial de la Fig. 2.1.2 est une réalisation géométrique de ce complexe simplicial abstrait.
Considérons maintenant le CSA {{a,b,c},{c,d,e},{a,b},{a,c},{b,c},{c,d},{d,e},{c, e},{a},{b},{c},{d},{e}}. Il est possible d’associer aux sommets a,b,c,d,e de ce CSA les sommets 1,2,3,4,5 de la Fig. 2.1.2 (dans l’ordre). Avec cette association, chaque simplexe du CSA correspond à un simplexe du complexe simplicial. Mais ce n’est pas une réalisation géométrique de ce CSA car dans ce cas les contraintes géométriques du complexe simplicial ne sont pas vérifiées. La Fig. 2.4 montre un complexe simplicial qui est la réalisation géométrique de ce CSA.
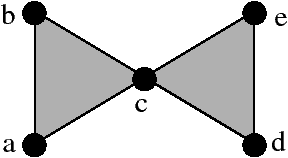
Figure 2.4: Un complexe simplicial qui est la réalisation géométrique du complexe simplicial abstrait {{a,b,c},{c,d,e},{a,b},{a,c},{b,c},{c,d},{d,e},{c,e},{a},{b},{c},{d}, {e}}.
Les complexes cellulaires abstraits [Mun84, Kle00, KR04, Kov08] étendent les complexes simpliciaux abstraits pour ne plus considérer uniquement des simplexes mais des cellules quelconques. Par rapport aux complexes simpliciaux abstraits, il faut désormais ajouter la notion de dimension qui était avant implicite de par la nature régulière des simplexes, et expliciter la relation de face entre les cellules.
Les éléments de C sont les cellules du complexe, et la relation ≼ est la relation de face. Les faces d’une cellule c sont toutes les cellules c′ tel que c′ ≼ c. Cette relation permet de définir la notion d’incidence et d’adjacence. Deux cellules sont incidentes si l’une est la face de l’autre, et deux cellules c et c′ sont adjacentes si dim(c)=dim(c′) et ∃ f ∈ C, tel que f est une face de c et une face de c′.
De manière similaire aux complexes simpliciaux abstraits, la dimension d’un complexe cellulaire abstrait C est la plus grande dimension d’une cellule de C, et une cellule est dite principale si elle n’est la face d’aucune cellule du complexe.
Un invariant topologique est une propriété qui se conserve par homéomorphisme : les invariants topologiques de deux objets homéomorphes sont égaux. La dimension de l’objet ou son nombre de composantes connexes sont deux exemples d’invariants topologiques.
La caractéristique d’Euler-Poincaré est le plus connu des invariants topologiques. Pour un complexe cellulaire, elle se définit simplement par la somme alternée du nombre de cellules de chaque dimension (cf. Def. 13). Comme cette caractéristique est un invariant topologique, elle ne dépend pas de la décomposition cellulaire. De plus, elle est réunion-additive, c’est-à-dire que la caractéristique d’Euler-Poincaré d’un objet qui est l’union disjointe de deux objets est la somme des deux caractéristiques de ces objets.
Nous présentons Fig. 2.5 un exemple de calcul de la caractéristique d’Euler-Poincaré pour deux subdivisions différentes d’un tore. Dans le premier cas, le complexe cellulaire est composé de neuf 0-cellules, dix-huit 1-cellules et neuf 2-cellules. χ=9−18+9=0. Dans le second cas, le complexe cellulaire est composé de seize 0-cellules, trente-deux 1-cellules et seize 2-cellules. χ est donc à nouveau égale à 0.
Les nombres de Betti (notés bi pour le nombre de Betti en dimension i) sont des invariants topologiques qui, intuitivement, comptent le nombre de «trous» dans chaque dimension. Par exemple, pour un objet 3D, b0 compte le nombre de composantes connexes, b1 compte le nombre de tunnels (appelés parfois anses) et b2 compte le nombre de cavités (appelées parfois trous). Pour un objet nD, les nombres de Betti bk pour k>n sont tous égaux à zéro. Pour l’exemple de la Fig. 2.1.4, b0=1, b1=3 et b2=2, et pour celui de la Fig. 2.1.4, b0=2, b1=3 et b2=1.
[a][b]

Figure 2.6: Nombres de Betti en dimension 3. Les objets représentés ici sont «pleins». (a) Complexe cellulaire 3D composé d’une composante connexe : b0=1 ; de trois tunnels : b1=3 ; et de deux cavités: b2=2 : χ=1. (b) Complexe cellulaire 3D composé de deux composantes connexes : b0=2 ; de trois tunnels : b1=3 ; et d’une cavité : b2=1 : χ=1.
La caractéristique d’Euler-Poincaré peut également être définie comme la somme alternée des nombres de Betti (Def. 14), et les deux définitions sont équivalentes (cf. [Hat02]).
Par cette définition, deux complexes cellulaires ayant mêmes nombres de Betti ont la même caractéristique d’Euler-Poincaré. Mais l’inverse n’est pas vrai : deux complexes ayant la même caractéristique d’Euler-Poincaré n’auront pas forcément les mêmes nombres de Betti comme nous pouvons le voir sur l’exemple de la Fig. 2.6. De ce fait, les nombres de Betti sont des invariants topologiques «plus puissants» que la caractéristique d’Euler-Poincaré car ils permettent de différencier plus de complexes cellulaires que la caractéristique d’Euler-Poincaré.
Les nombres de Betti sont liés aux groupes d’homologie, un autre invariant topologique. Plus précisément, le nombre de Betti bi est le rang du ième groupe d’homologie. Cet invariant est encore plus puissant que les nombres de Betti car il décrit les trous des objets en terme de cycles de cellules et pas uniquement en les comptant. De ce fait, il représente les torsions de l’objet (les parties d’un objet non orientable qui ont été recollées «à l’envers») qui ne sont pas prises en compte dans les nombres de Betti. Par contre la caractéristique d’Euler-Poincaré et les nombres de Betti sont plus simples à manipuler car ils sont définis directement comme des valeurs numériques.
En 2D, le Théorème 1 de classification des surfaces (qui date des années 1860, mais qui est donné par exemple dans [Lee00]) prouve que toute surface peut se caractériser par son orientation et sa caractéristique d’Euler-Poincaré.
La somme connexe de deux surfaces M et N, notée M#N, est obtenue en enlevant un disque (homéomorphe à B2) de chacune des deux surfaces, et en recollant les deux surfaces le long des deux bords créés. La caractéristique d’Euler-Poincaré de la somme connexe est calculée à partir de la somme des caractéristiques de chaque surface moins les deux disques : χ(M#N)=χ(M)+χ(N)−2.
Les deux premières familles du théorème de classification sont les surfaces orientables. Dans ces deux cas, le nombre g, appelé le genre, est le nombre de tores utilisés dans la somme connexe (donc 0 dans le cas de la sphère). Comme la sphère et le tore ont comme caractéristique d’Euler-Poincaré respectivement 2 et 0, en utilisant la formule précédente sur la caractéristique d’Euler-Poincaré d’une somme connexe, nous obtenons que χ(c)=2−2g (dans le cas d’un tore, cf. exemple de la Fig. 2.5, nous avons χ=0 et g=1).
Dans le troisième cas, la surface est non-orientable. La caractéristique d’Euler-Poincaré d’un plan projectif est 1, et en utilisant la formule sur la caractéristique d’Euler-Poincaré d’une somme connexe, nous obtenons que χ(c)=2−k.
De ce fait, toute surface 2D fermée est déterminée de manière unique par sa caractéristique d’Euler-Poincaré et son orientabilité, ce qui classifie totalement les surfaces 2D fermées. Cette classification s’étend aux surfaces ouvertes en ajoutant comme caractéristique le nombre de bords. Il faut noter que ce type de classification n’existe pas en dimension supérieure dans le cas général.
Manipuler les complexes simpliciaux ou cellulaires décrits dans la section précédente revient à manipuler des ensembles et à utiliser des opérations ensemblistes. De ce fait, les algorithmes permettant de retrouver les relations entre les cellules (comme par exemple toutes les cellules adjacentes à une cellule donnée) sont coûteux car non limités aux voisinages des cellules (pour les cellules adjacentes à une cellule donnée, nous devons parcourir toutes les cellules de l’ensemble).
Pour ces raisons, plusieurs travaux se sont intéressés à la définition de structures combinatoires permettant de représenter ces modèles. Pour chaque structure, l’important est d’être capable de représenter les cellules et les relations d’adjacence et d’incidence entre ces cellules, mais également d’avoir une interprétation topologique de la structure par rapport à l’espace représenté. C’est pour cette raison que des contraintes de cohérence sont définies.
Un ensemble semi-simplicial [May67, FP90, EL94, Lan95, LL95] est un modèle algébrique représentant des simplexes et des relations d’incidence. Il est possible d’associer un ensemble semi-simplicial à tout complexe simplicial, mais le contraire n’est pas vrai. En effet, un ensemble semi-simplicial présentant des relations de multi-incidence ne pourra pas être représenté par un complexe simplicial contenant la relation de multi-incidence (cf. exemple Fig. 2.2.1). La réalisation géométrique d’un tel ensemble sera alors un CW-complexe.
La Def. 15 donne la définition des ensembles semi-simpliciaux qui, contrairement aux complexes simpliciaux, contiennent explicitement les relations de face entre les simplexes.
Les éléments de Kp sont les simplexes de dimension p (ou p-simplexes), et les applications dip sont les opérateurs de face des simplexes donnant pour chaque p-simplexe les (p−1)-simplexes de son bord. Il y a p+1 (p−1)-simplexes dans le bord d’un p-simplexe, chacun est obtenu par un dip différent, pour i allant de 0 à p. De manière générale et afin de simplifier les notations, dip est parfois noté di. Les relations djp−1(dip(s))=di−1p−1(djp(s)) garantissent la cohérence de la structure simpliciale. Par exemple, ces relations garantissent qu’un triangle est bordé par trois sommets. Intuitivement, ces relations indiquent que le simplexe obtenu par le chemin djp−1(dip) est le même que celui obtenu par le chemin di−1p−1(djp). Sans ces contraintes, un triangle pourrait avoir jusqu’à six sommets dans son bord. Il faut noter que les ensembles semi-simpliciaux sont sans opérateur de dégénérescence10 contrairement aux ensembles simpliciaux (que nous ne détaillons pas ici).
Nous pouvons voir un exemple d’ensemble semi-simplicial Fig. 2.2.1, et vérifier que les contraintes de cohérence sont satisfaites : par exemple d1(d2(1))=d1(d1(1)) et d0(d2(1))=d1(d0(1)).
[a][b]
[c]
Figure 2.7: Exemple de complexe simplicial et d’ensemble semi-simplicial. (a) Un complexe simplicial C composé de cinq 0-simplexes (étiquetés de a à e), six 1-simplexes et deux 2-simplexes. (b) Un ensemble semi-simplicial correspondant à C. Les deux 2-simplexes sont numérotés 1 et 2. (c) Un ensemble semi-simplicial qui ne correspond pas à un complexe simplicial à cause de la multi-incidence.
Le bord d’un i-simplexe s est l’ensemble des j-simplexes s′, avec 0≤ j < i, tels que s′ est une face de s. L’étoile est la relation inverse : l’étoile d’un i-simplexe s est l’ensemble des j-simplexes s′, avec i< j ≤ n, tels que s est une face de s′.
Les premiers travaux autour des cartes combinatoires [Edm60, Tut63, Jac70, Cor73, Cor75] avaient pour objectif de définir une structure de données permettant de manipuler un graphe planaire11 plongé12 sur un plan. Ces travaux ont été réalisés au sein de la communauté de la théorie des graphes dans le cadre d’études de propriétés des graphes planaires. Nous présentons ici ces travaux uniquement dans le but de donner une vision de l’historique des cartes, car ces notions sont maintenant comprises dans la définition nD des cartes combinatoires présentées Section 2.2.3.
Lorsqu’un graphe est plongé dans le plan, les arêtes peuvent être ordonnées autour des sommets et il est possible alors de définir une application donnant pour chaque arête, l’arête suivante autour d’un sommet. Mais un problème se pose : une même arête a deux successeurs différents, un pour chacun de ses deux sommets. La solution à ce problème consiste à découper chaque arête du graphe en deux éléments (appelés donc demi-arêtes ou brins). De ce fait, un brin étant incident à un seul sommet, il a un unique successeur. Par contre, il faut ajouter une relation entre les deux brins issus de la même arête. La relation donnant, pour un brin, son brin successeur autour d’un sommet a été appelée σ (s pour sommet) et celle donnant l’autre brin issu de la même arête a été appelée α (a pour arête). Comme chaque arête est représentée par deux brins, appliquer α deux fois à partir d’un brin b redonne le brin b : α est une involution. Par contre, σ est une permutation : à partir d’un brin b, appliquer σ plusieurs fois (mais pas nécessairement deux fois) permet de revenir sur b.
Une carte combinatoire 2D est donc un ensemble de brins B plus une involution α et une permutation σ, notée C=(B,α,σ). Par construction, le nombre de brins d’une carte combinatoire est le double du nombre d’arêtes du graphe. Il faut noter que les sommets du graphe ne sont pas représentés explicitement dans la carte combinatoire. En effet, un sommet est l’ensemble des brins obtenus en partant d’un brin b et en utilisant l’application σ jusqu’à retomber sur le brin de départ b.
Comme une carte combinatoire représente un graphe planaire plongé, les cycles d’arêtes délimitent des zones de l’espace appelées faces. Étant donné un brin b, la face déterminée par b s’obtient en utilisant σ ∘ α (noté ϕ, f pour face) jusqu’à retomber sur le brin de départ b. Les faces parcourues à l’aide de la permutation ϕ sont toutes parcourues avec la même orientation, mais le choix d’une orientation est arbitraire. De plus, il faut noter la présence d’une face infinie (appelée également face externe ou face englobante) qui «entoure» les autres faces.
La Fig. 2.8 présente un exemple de graphe planaire (Fig. 2.2.2), et la carte combinatoire 2D correspondante qui peut être dessinée de deux manières différentes (Fig. 2.2.2 où deux brins en relation par α sont dessinés comme une arête du graphe, et Fig. 2.2.2 où deux brins en relation par α sont dessinés comme deux segments parallèle). Le sommet d du graphe correspond à l’ensemble de brins {6,8,14,15} obtenu par exemple à partir du brin 6 en utilisant l’application σ; la carte de cet exemple comporte sept sommets. La face délimitée par les sommets (c,d,f,e) du graphe correspond à l’ensemble de brins {2,4,6,7} et s’obtient par exemple à partir du brin 2 en tournant autour de la face à l’aide de ϕ : ϕ(2)=7, ϕ(7)=6, ϕ(6)=4 et ϕ(4)=2. Sur cet exemple, le choix d’orientation fait que l’intérieur de la face se trouve à droite de l’arête courante, en suivant cette arête selon son orientation. La face {1,3,10,12,14,16,18} est la face infinie. Notez que la règle d’orientation est vérifiée même pour la face infinie : l’intérieur de la face, qui se trouve à l’extérieur de l’objet, se situe bien à main droite de chaque arête de la face. Cette carte contient quatre faces : trois faces bornées et une face infinie.
[a][b]
[c]
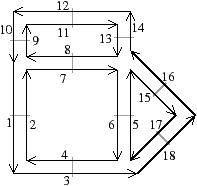
Figure 2.8: La représentation d’un graphe planaire à l’aide d’une carte combinatoire. (a) Un graphe planaire plongé dans le plan. (b) La carte combinatoire correspondante. Les brins sont numérotés de 1 à 18. La relation σ est représentée par les flèches grises (par exemple σ(1)=7), et deux brins en relation par α sont dessinés comme un seul segment avec une barre perpendiculaire séparant les deux éléments (par exemple α(1)=2). (c) Une seconde manière de dessiner la même carte combinatoire. Un brin est représenté par une flèche, deux brins en relation par α sont dessinés parallèlement, avec des orientations opposées (par exemple α(1)=2), et reliés par un petit segment gris. Deux brins en relation par ϕ sont dessinés de manière consécutive (par exemple ϕ(1)=3). Ce type de dessin fait apparaître plus clairement les faces de la carte, alors que la première manière fait apparaître plus clairement les sommets.
Une carte combinatoire est définie à l’aide d’une involution et une permutation, l’autre permutation étant implicite car c’est la composition des deux premières applications. Il existe deux cartes combinatoires duales l’une de l’autre selon que la permutation de la carte représente les sommets σ (comme dans le paragraphe et l’exemple précédent) ou ϕ comme dans l’exemple de la Fig. 2.9. Plus précisément, soit C=(B,α,σ) une carte combinatoire, la carte combinatoire duale est C=(B,α,ϕ). Ces cartes sont duales car les sommets de l’une correspondent aux faces de l’autre et réciproquement.
La Fig. 2.9 montre le graphe dual et la carte combinatoire duale du graphe et de la carte présentés Fig. 2.8. La carte est composée de quatre sommets et de sept faces, car la carte de la Fig. 2.2.2 est composée de sept sommets et de quatre faces. Nous pouvons vérifier sur cet exemple que σ de la carte duale égale ϕ de la carte initiale et réciproquement. Il faut faire attention à distinguer les deux représentations graphiques d’une même carte combinatoire (comme par exemple les deux cartes Fig. 2.2.2 et Fig. 2.2.2) et les deux cartes combinatoires duales (comme par exemple les deux cartes Fig. 2.2.2 et Fig. 2.2.2) qui ne sont pas les mêmes cartes.
[a][b]
[c]
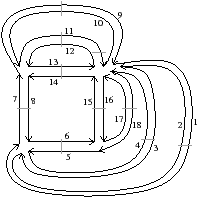
Figure 2.9: Carte combinatoire duale. (a) Le multi-graphe dual (en noir) du graphe de la Fig. 2.2.2 (dessiné ici en gris). Ce multi-graphe s’obtient en mettant un sommet par face du graphe initial et en mettant autant d’arêtes entre deux sommets que le nombre de fois que les deux faces correspondantes dans le graphe initial sont voisines. (b) La carte combinatoire correspondante qui est donc la carte duale de la carte présenté Fig. 2.2.2. (c) La même carte dessinée de la seconde manière.
Bien que définies initialement comme une représentation des graphes planaires plongés, les cartes combinatoires 2D permettent de représenter toute subdivision de n’importe quelle surface orientable fermée. Dans le cas des graphes planaires plongés, ce sont des subdivisions de la sphère (et non du plan à cause de la face infinie). Mais une carte combinatoire 2D peut représenter une subdivision d’un tore comme sur l’exemple de la Fig. 2.2.2 ou d’un tore à deux trous comme sur l’exemple de la Fig. 2.2.2 (de manière générale, le théorème de classification des surfaces dit que toute surface orientable fermée est homéomorphe soit à une sphère soit à un tore à k trous). Étant donnée une carte combinatoire 2D, le type de la surface correspondante peut se calculer en utilisant la caractéristique d’Euler-Poincaré.
[a][b]
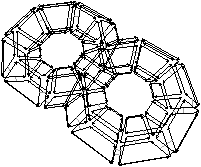
Figure 2.10: Deux exemples de cartes combinatoires 2D n’étant pas des subdivisions de la sphère (les nombres de cellules sont calculés par programme). (a) Une subdivision d’un tore. La carte est composée de 32 sommets, 64 arêtes et 32 faces : χ=0. (b) Une subdivision d’un tore à deux trous. La carte est composée de 82 sommets, 148 arêtes et 64 faces : χ=−2.
Enfin, une carte combinatoire 2D est équivalente à la structure des demi-arêtes [Wei85, Wei88] (en anglais half-edges) très utilisée en modélisation géométrique et en géométrie algorithmique. Il existe en effet une bijection entre les éléments de la structure en demi-arêtes (les demi-arêtes) et les éléments de la carte combinatoires 2D (les brins). Chaque demi-arête est associée avec la demi-arête suivante (ϕ dans la carte), éventuellement la demi-arête précédente (ϕ−1 dans la carte), et la demi-arête opposée (α dans la carte). Différentes implémentations des demi-arêtes ajoutent des relations liant chaque demi-arête avec le sommet incident, et/ou avec la face incidente. C’est également possible de manière équivalente pour les cartes combinatoires, et il est alors possible de formaliser les contraintes que doivent vérifier ces relations à l’aide de la notion d’orbite. Il existe plusieurs variantes de cette structure comme les arêtes ailées, les quad-edges, les DCEL…[Bau75, MP78, GS85, Män88, dBvKOS00] qui sont toutes très proches et peuvent être considérées comme des variantes du même principe original.
Les cartes combinatoires 2D ont été ensuite étendues en 3D [AK88, AK89, Lie88, Spe91] avant d’être définies de manière générique en nD [Lie89, Lie91, Lie94]. Elles permettent de représenter un complexe cellulaire orientable fermé, en décrivant les cellules du complexe ainsi que les relations d’adjacence et d’incidence entre ces cellules. Nous parlons de n-carte pour une carte combinatoire de dimension n.
Les cartes combinatoires permettent de représenter les quasi-variétés orientables fermées13. La notion de quasi-variété est introduite ici, comme une sous classe des pseudo-variétés [Elt94].
Cette notion est différente de la notion de variété topologique de dimension n classique [Ago76, Tak91] pour laquelle chaque point doit avoir un voisinage homéomorphe à une boule ouverte de dimension n (ou à une demi-boule ouverte si la variété topologique est à bord). De ce fait, une quasi-variété n’est pas forcément une variété [Lie93], excepté en dimension 2 (cf. exemple Fig. 2.11).
[a][b]
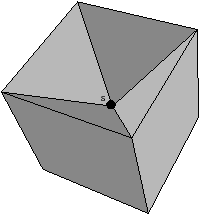
Figure 2.11: Exemple de quasi-variété qui n’est pas une variété. (b) Ce complexe cellulaire 3D est une quasi-variété car il est obtenu en collant les quatre pyramides de (a) le long de leurs faces (2-cellules). Par contre ce n’est pas une variété car le voisinage du point s n’est pas homéomorphe à la demi-boule ouverte h(B1/2)3 (c’est la demi boule qui est considérée car s est un point du bord).
Cette notion est incluse dans la notion de pseudo-variété présentée Section 2.1, mais n’est pas égale. En effet, dans la notion de quasi-variété, l’adjacence entre deux cellules de dimension n est nécessairement réalisée par une (n−1)-cellule, ce qui n’est pas le cas pour les pseudo-variétés. L’exemple de pseudo-variété donné Fig. 2.3 n’est pas une quasi-variété car il n’est possible à obtenir en collant des 2-cellules le long de 1-cellules.
Une n-carte peut s’obtenir de manière intuitive par décompositions successives des cellules d’un objet donné, comme présenté Fig. 2.12 pour un objet 2D.
[a][b]
[c]
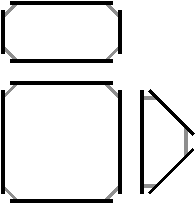
Figure 2.12: La décomposition d’un objet pour obtenir la carte combinatoire correspondante. (a) Un objet 2D (la face infinie n’est pas représentée). (b) Les faces de cet objet (sans la face infinie). (c) Les arêtes de ces faces.
À partir de l’objet à représenter Fig. 2.2.3, qui doit être fermé et orientable, nous commençons par distinguer les faces de cet objet Fig. 2.2.3, en conservant les relations d’adjacence entre chaque couple de faces (représentées par les traits noirs). Puis nous distinguons les arêtes de ces faces Fig. 2.2.3, en conservant les relations d’adjacence entre chaque couple d’arêtes (représentées par les traits gris).
L’objet initial a été décomposé en un ensemble d’éléments, les brins, qui constituent les briques de base de la définition des cartes combinatoires. Il faut ensuite reporter les différentes relations d’adjacence sur ces éléments. La relation d’adjacence entre les arêtes est représentée par une permutation, qui pour chaque brin donne le brin suivant de la même face (en respectant une orientation donnée). Cette relation est notée β1, car elle met en relation des arêtes qui sont des cellules de dimension 1. La relation d’adjacence des faces est représentée par une involution, β2, étant donné qu’elle met en relation des cellules de dimension 2 (par rapport aux notations 2D de la section précédente, β1 correspond à ϕ et β2 à α, l’intérêt de la notation βi étant sa généralisation en dimension quelconque).
Nous pouvons voir Fig. 2.2.3 la carte combinatoire de l’objet présenté Fig. 2.2.3 ainsi que la convention graphique généralement utilisée dans les schémas de cartes combinatoires.
[a][b]
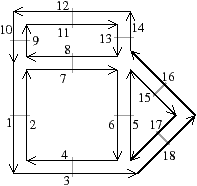
Figure 2.13: Exemple de carte combinatoire 2D et convention graphique. (a) Un objet 2D. (b) La carte combinatoire correspondante. Un brin est représenté par une flèche noire, éventuellement numéroté lorsque nécessaire. Deux brins en relation par β1 sont dessinés de manière consécutive (par exemple β1(1)=3). Deux brins en relation par β2 sont dessinés parallèles, proches et inversés, avec un petit segment perpendiculaire reliant les deux brins (par exemple β2(1)=2).
Cette méthode de décomposition d’un objet peut s’utiliser pour n’importe quelle dimension. Nous pouvons voir un second exemple de construction d’une carte combinatoire à partir d’un objet Fig. 2.14, mais cette fois pour la dimension 3.
[a][b]
[c]
[d]
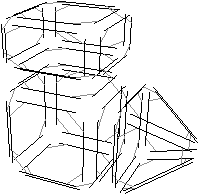
Figure 2.14: La décomposition d’un objet 3D pour obtenir la carte combinatoire correspondante. (a) Un objet 3D. (b) Les volumes de cet objet. (c) Les faces de ces volumes. (d) Les arêtes de ces faces.
L’objet présenté Fig. 2.2.3 est décomposé successivement pour distinguer ses volumes Fig. 2.2.3, puis les faces de ces volumes Fig. 2.2.3 et enfin les arêtes de ces faces Fig. 2.2.3. Les éléments obtenus sont les brins de la carte combinatoire représentant l’objet initial. Il faut maintenant reporter les relations d’adjacence entre chaque cellule sur les brins. Il existe, comme pour la dimension 2, une permutation β1 qui met en relation un brin et le brin suivant de la même face, et une involution β2 qui met en relation deux brins de deux faces adjacentes d’un même volume. Une involution supplémentaire β3 met en relation deux volumes adjacents. La carte combinatoire obtenue est représentée Fig. 2.2.3.
[a][b]
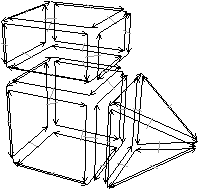
Figure 2.15: Exemple de carte combinatoire 3D et convention graphique (représentation partielle, le volume infini n’est pas dessiné). (a) Un objet 3D. (b) La carte combinatoire correspondante. La convention graphique utilisée est la même qu’en 2D. Généralement l’involution β3 n’est pas représentée car elle peut se retrouver sans ambiguïté par la forme des faces.
Cette méthode de construction permet d’appréhender les cartes combinatoires de manière intuitive. La Def. 17 donne la définition formelle des cartes combinatoires nD ce qui nous permettra par la suite d’utiliser ses propriétés algébriques. Nous trouvons cette définition par exemple dans [Lie94].
Les brins sont ici une notion abstraite, et servent uniquement de support pour les différentes applications. Seul β1 est une permutation, les autres βi sont des involutions. La dernière ligne de cette définition pose des contraintes sur la manière dont les brins sont mis en relation pour garantir que les objets représentés sont des quasi-variétés (cette contrainte ne s’applique pas pour n<3). Par exemple, en 3D, la contrainte ajoutée est que β1∘β3 doit être une involution, ce qui revient à dire que lorsque nous mettons deux brins de deux faces différentes en relation pour β3, nous devons obligatoirement mettre tous les autres brins de ces deux faces en relation deux à deux par β3.
Nous ajoutons dans cette définition la contrainte sur βi qui doit être sans point fixe, ∀ i: 2 ≤ i ≤ n qui n’est pas présente dans [Lie94], ceci pour éviter des configurations particulières, mais ausi pour être homogène avec la définition des G-cartes (présentée section suivante).
En effet, un brin b tel que βi(b)=b, pour un i: 2 ≤ i ≤ n correspond à replier une arête sur elle même. Nous obtenons alors une configuration où une arête n’a qu’un seul sommet dans son bord. Il est alors très difficile dans ce cas de faire un lien avec une représentation cellulaire
La deuxième raison concerne le lien avec les G-cartes. En effet, pour une G-carte, un brin b point fixe pour αi est un brin considéré sans successeur (et non comme son propre successeur). Ce cas est possible pour les G-cartes car elles peuvent représenter des objets ouverts, mais n’est pas possible ici car les cartes considérées doivent être fermées.
Interdire les points fixes évite les configurations particulières, et évite le problème de différentes interprétations pour les cartes et les G-cartes. Par contre, nous conservons la possibilité pour β1 de comporter des points fixes car un brin b tel que β1(b)=b correspond au cas des boucles (c-à-d une arête incidente deux fois au même sommet) qui n’est pas une configuration particulière (dans ce type de cas, l’arête a deux sommets dans son bord même si c’est deux fois le même).
Les motivations de [Lie94] pour autoriser les points fixes pour βi étaient de pouvoir convertir n’importe quelle G-carte orientable en carte combinatoire (cf. Section 2.2.4). Nous pensons que l’ajout de contraintes sur les βi qui doivent être sans point fixe rend les choses plus simples pour les cartes combinatoires et plus homogènes, mais cela a pour inconvénient de nous obliger à restreindre légèrement la convertion de G-carte en carte.
Revenons à la définition des cartes combinatoires. Comme les cartes sont fermées, nous allons avoir, de manière similaire à la dimension 2, la présence d’une n-cellule infinie par composante connexe de la carte qui «entoure» complètement la composante et permet de représenter une quasi-variété fermée. Nous notons β0 la permutation β1−1 , et βij la composition βj∘βi. Lorsque deux brins b1 et b2 sont tels que βi(b1)=b2, nous disons que b1 est i-cousu à b2. Étant donné que les βi, pour i ≠ 1, sont des involutions, si b1 est i-cousu à b2 alors b2 est i-cousu à b1. Remarquons que chaque brin possède forcément une image pour chaque βi, étant donné que ces βi sont des bijections. L’opération consistant à mettre en relation deux brins pour βi est appelée i-couture.
Une carte combinatoire est orientée. Le choix de l’orientation est une convention qu’il faut définir, puis conserver afin que toutes les opérations soient homogènes. La carte combinatoire d’orientation inverse (cf. Def. 18) est obtenue simplement en remplaçant β1 par son inverse β0. Par exemple, la carte de la Fig. 2.2.3 est l’inverse de la carte de la Fig. 2.2.3. Il est immédiat de prouver que l’inverse d’une carte combinatoire est une carte combinatoire, ainsi que de prouver que l’inverse de l’inverse d’une carte est la carte initiale.
Une carte combinatoire ne représente pas les cellules de manière explicite, mais de manière implicite comme des ensembles de brins obtenus à l’aide de la notion d’orbite. Chaque i-cellule est une orbite particulière (cf. Def. 19). Pour simplifier les écritures, nous notons ⟨h(βi1,…,βik)⟩ pour l’orbite contenant toutes les permutations possibles sauf celles-là, c-à-d ⟨{β1,…,βn}∖{βi1,…,βik}⟩. Nous utilisons également la notation ensembliste ⟨h(I)⟩, avec I={βi1,…,βik} pour l’orbite ⟨h(βi1,…,βik)⟩. Enfin, pour simplifier les notations des orbites, nous employons indifféremment ⟨{βi1,…,βik}⟩ ou ⟨βi1,…,βik⟩ car cela n’entraîne aucune ambiguïté.
Il y a deux cas différents. L’un pour la définition des 0-cellules (les sommets), et l’autre pour les autres cellules. Cela provient du fait que β1 est une permutation alors que les autres βi sont des involutions : les cartes combinatoires n’ont pas une définition homogène (ce problème est résolu dans la définition des cartes généralisées que nous présentons Section 2.2.4).
Une i-cellule incidente à un brin b peut se voir comme l’ensemble des brins que nous pouvons atteindre par un parcours d’origine b, en utilisant les β donnés dans l’orbite ainsi que leurs inverses. Dit autrement, c’est l’ensemble des brins b′ tel qu’il existe un chemin entre b et b′ utilisant uniquement les β donnés ainsi que leurs inverses. Les 0-cellules sont définies ainsi, car nous parcourons uniquement un brin sur deux, afin de n’atteindre que les brins «sortants» du sommet incident à b. Les autres i-cellules sont simplement l’orbite composée de tous les β sauf βi. En effet, comme βi permet de changer de i-cellule, en l’enlevant de l’orbite nous restons au cours du parcours sur les brins de la même i-cellule. Remarquons enfin que chaque ensemble de i-cellules est une partition de l’ensemble des brins de la carte. Chaque brin appartient donc exactement à chaque i-cellule, ∀ i∈{0,…,n}.
Sur l’exemple de la Fig. 2.2.3, le sommet incident au brin 7 est l’ensemble des brins de l’orbite ⟨β02⟩(7)= {5,7,13,16}. L’arête incidente au brin 7 est l’ensemble des brins de l’orbite ⟨β2⟩(7)= {7,8} (dans une carte combinatoire 2D, une arête est toujours composée de deux brins, ce n’est plus vrai en dimension supérieure). Enfin, la face incidente au brin 7 est l’ensemble des brins de l’orbite ⟨β1⟩(7)= {2,4,6,7}.
C’est la définition des 0-cellules qui rend nécessaire la condition dans la définition des cartes combinatoires que les βi, pour i>1, doivent être sans point fixe. En effet, si un brin b est tel que βi(b)=b, alors β0i−1(b)=βi1=β1(b) : le brin β1(b) appartient à la même orbite sommet que celle du brin b. Cela pose problème, car le fait d’enlever un brin d’une carte va avoir pour effet de bord de fusionner des orbites sommets, alors que cette modification simple n’est pas censée modifier les sommets (ce problème est résolu Section 2.2.5 avec l’introduction des cartes ouvertes).
Avec cette définition des i-cellules, la notion d’incidence se définit simplement en étudiant l’intersection des ensembles de brins des deux cellules (cf. Def. 20).
La Def. 21 définit alors la notion d’adjacence entre deux cellules en utilisant la notion d’incidence.
Pour n’importe quel brin b, βi(b) permet de changer de i-cellule (∀ i: 1≤ i≤ n), c’est-à-dire d’obtenir un brin b′ appartenant à la i-cellule adjacente à la i-cellule contenant b le long de la (i−1)-cellule contenant b15, mais change également de 0-cellule (pour i=1, car nous allons sur l’arête suivante de la même face, et pour i, 2≤ i≤ n, car deux brins en relation par βi sont d’orientations opposées). Comme dans le cas précédent cette seconde 0-cellule peut-être égale à la première dans le cas des boucles, c-à-d une arête incidente deux fois au même sommet.
Sur l’exemple de la Fig. 2.2.3, la 1-cellule c1(7)={7,8} est incidente à la 2-cellule c2(2)={2,4,6,7}, et la 2-cellule c2(9)={8,9,11,13} est adjacente à c2(2) car elles sont toutes deux incidentes à la 1-cellule c1(7). À partir du brin 8 incident à c0(8)={2,8,10} et c2(8)={8,9,11,13}, en effectuant β2(8) nous obtenons le brin 7 incident à c0(7)={5,7,13,16} et c2(7)={2,4,6,7} : nous avons changé de 0-cellule et de 2-cellule.
La notion de chemin entre deux brins se définit simplement comme une suite de brins en liaison deux à deux par des β (cf. Def. 22). Sur l’exemple de la Fig. 2.2.3, la séquence (1,2,4,6,5,15) est un chemin obtenu à partir du brin 1 et utilisant successivement β2, β1, β1, β2, β0.
Cette notion de chemin peut servir, comme en théorie des graphes, à définir la notion de connexité (cf. Def. 23).
La Def. 24 donne une seconde définition de la connexité, équivalente à la précédente, mais qui utilise la notion d’orbite au lieu de la notion de chemin.
Il suffit de tester la propriété pour un brin b ∈ B. En effet, si pour ce brin ⟨β1,…,βn⟩(b) =B, alors tous les brins de B appartiennent à cette orbite et la propriété est donc vraie pour chaque brin de B. Par contre si la propriété n’est pas vraie pour ce brin, alors il existe au moins un brin n’appartenant pas à la même orbite que b et donc quel que soit le brin considéré, son orbite ne contiendra jamais tous les brins.
La Def. 25 définit la notion de cartes isomorphes. Intuitivement deux cartes sont isomorphes s’il existe une bijection entre leur brins respectant les relations d’adjacence.
| ∀ i ∈ {1,…,n}, ∀ b ∈ B, f(βi(b))=βi′(f(b)) |
Un automorphisme est un isomorphisme entre une carte et elle même.
Lorsque nous considérons une subdivision d’un espace de dimension n, considérer l’espace dual revient à inverser les dimensions de l’espace de 0 à n en n à 0. De ce fait, une i-cellule dans l’espace initial va devenir une (n−i)-cellule dans l’espace dual. Cette transformation conserve les relations d’incidence et d’adjacence données dans les Def. 20 et Def. 21. Nous pouvons définir la carte combinatoire duale d’une carte donnée en gardant les mêmes brins, et en inversant l’ordre des permutations pour refléter ces changements de dimension. De plus, il faut composer les permutations βn−1, …, β1 avec βn pour obtenir une permutation (βn(n−1)) et des involutions (βni pour 1≤ i <n−1). Enfin, pour garantir que les βi, pour 2≤ i≤ n, sont sans point fixe, nous devons ajouter la contrainte que βn∘βi soit sans point fixe (ce qui revient à éviter un brin b tel que βn(b)=βi(b), ce qui un cas très particulier non utilisé dans les cas pratiques).
Un exemple de carte duale est donnée en 2D dans la Fig. 2.17. La 2-carte est C=(B,β1,β2) et sa carte duale C=(B,β21,β2). La Prop. 1 prouve la validité de la Def. 26 en montrant que la duale d’une carte combinatoire est une carte combinatoire.
[a][b]
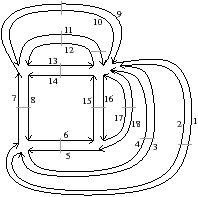
Figure 2.17: Exemple de cartes combinatoires duales. (a) Une 2-carte C=(B,β1,β2), composée de 7 sommets, 9 arêtes, et 4 faces. (b) La carte duale de C, C=(B,β1′,β2′)=(B,β21,β2), composée de 4 sommets, 9 arêtes, et 7 faces. Par exemple, β1′(6)=β21(6)=15.
Nous prouvons ici les deux propriétés principales liées à la définition des cartes duales : (1) la duale d’une carte est une carte ; (2) une i-cellule incidente à b d’une carte correspond à la (n−i)-cellule incidente à b dans la carte duale. Nous devons re-prouver ces propriétés déjà évoquées dans [Lie94] à cause de la contrainte supplémentaire que nous avons ajoutée.
Proof. Pour n=1, la preuve est immédiate car C=(B,β1), donc C=(B,β1−1) est une carte combinatoire.
Pour n>1. Tout d’abord, chaque βni, pour 1≤ i≤ n−2 est bien une involution par définition des cartes. βn est également une involution (car n ≥ 2), et βn(n−1) une permutation. Le fait que les involutions sont sans point fixe se déduit directement des préconditions sur les βn∘βi qui sont sans point fixe. Les 3 premières conditions de la Def. 17 sont donc vérifiées. En notant C=(B,β1′,…,βn′), la dernière condition de la définition des cartes combinatoires s’écrit ∀ i,j: 1 ≤ i<i+2≤ j ≤ n, βi′∘βj′ est une involution.
En re-écrivant les β′ en fonction des β, cette condition se re-écrit en βn(n−i)∘βn est une involution ∀ i: 1 ≤ i ≤ n−2, et βn(n−i)∘βn(n−j) est une involution ∀ i,j: 1 ≤ i <i+2≤ j≤ n.
Commençons par la première écriture : β(n−i)∘βn∘βn=β(n−i) (car βn est une involution). Comme 1 ≤ i ≤ n−2, alors 2≤ n−i ≤ n−1, donc βn−i est une involution par définition de C et donc βn(n−i)∘βn est une involution.
Pour la seconde écriture, nous étudions βn(n−j)n(n−i), pour 1 ≤ i < i+2 ≤ j ≤ n. Comme 2<j, βn(n−j) est une involution donc égale à son inverse β(n−j)n. Donc βn(n−j)n(n−i)=β(n−j)nn(n−i)= β(n−j)(n−i). Comme i < i+2 ≤ j, β(n−j)(n−i) est une involution et donc βn(n−j)n(n−i) aussi.
La propriété principale de la dualité, énoncée dans la Prop. 2, est que toute i-cellule d’une carte devient une (n−1)-cellule dans la carte duale. Grâce à cette propriété, nous pouvons directement déduire que les relations d’incidence et d’adjacence sont identiques dans une carte et dans sa carte duale.
Proof. Par définition de la carte duale, nous avons C=(B,βn(n−1),…,βn1,βn).
Considérons tout d’abord le cas 1≤ i<n : par définition des cellules, nous avons ci(b)=⟨β1,…,βi−1,βi+1,…,βn⟩(b), et c′n−i(b)=⟨β1′,…,βn−i−1′,βn−i+1′,…,βn′⟩(b). En re-écrivant les β′, nous obtenons c′n−i(b)=⟨βn(n−1),…,βn(i+1),βn(i−1),…,βn1,βn⟩. Lorsqu’une orbite contient une fonction f∘ g et la fonction f, alors par propriété des orbites, cette orbite est équivalente à la même orbite dans laquelle nous remplaçons f∘ g par g. En effet, dans les deux cas, comme nous effectuons toutes les compositions des fonctions de l’orbite et de leurs inverses, nous obtenons le même résultat. En utilisant ce principe, c′n−i(b) peut se re-écrire en ⟨βn−1,…,βi+1,βi−1,…,β1,βn⟩, qui est donc égal à ci(b) (car l’ordre des permutations dans une orbite n’importe pas).
Considérons maintenant le cas i=0. c0(b)=⟨β02,…,β0n⟩(b), et c′n(b)=⟨β1′,…,βn−1′⟩(b). En re-écrivant les β′, nous obtenons c′n(b)=⟨βn(n−1),…, βn1⟩(b). Si n=2, alors la preuve est directe car c0(b)=⟨β02⟩, et c′2(b)=⟨β1′⟩=⟨β21⟩=⟨β02⟩. Si n>2, En utilisant la même règle que précédemment, l’orbite est identique à la même orbite dans laquelle nous composons tout les éléments sauf le dernier avec βn1. Nous obtenons l’orbite ⟨βn1n(n−1),…,βn1n2,βn1⟩(b). Comme n>2, alors βn1 est une involution donc égal à son inverse β0n. Nous pouvons donc re-écrire l’orbite en ⟨β0nn(n−1),…,β0nn2,βn1⟩(b), et donc en ⟨β0(n−1),…,β02,β0 n⟩(b), ce qui prouve que c0(b)=c′n(b).
Reste le cas i=n. cn(b)=⟨β1,…,βn−1⟩(b), et c′0(b)=⟨β02′,…,β0n′⟩(b). En re-écrivant les β′, nous obtenons c′0(b)=⟨β(n−1)nn(n−2),…,β(n−1)nn1,β(n−1)nn⟩, donc en simplifiant les βnn, nous obtenons directement ⟨β(n−1)(n−2),…,β(n−1)1,β(n−1)⟩. En combinant chaque membre sauf le dernier avec β(n−1), nous obtenons ⟨β(n−2),…,β1,β(n−1)⟩ ce qui prouve que cn(b)=c′0(b).
Nous pouvons vérifier cette propriété sur l’exemple précédent en vérifiant que chaque i-cellule de la carte de la Fig. 2.2.3 se transforme bien en une (2−i)-cellule dans la carte de la Fig. 2.2.3. Par exemple le sommet c0(10)={2,8,10} se transforme bien dans la face c′2(10) dans la carte duale, l’arête c1(10)={9,10} se transforme bien dans l’arête c′1(10) dans la carte duale, et la face c2(8)={8,9,11,13} se transforme bien dans le sommet c′0(8) dans la carte duale.
Les cartes généralisées sont une extension des cartes combinatoires permettant de représenter les quasi-variétés orientables ou non avec ou sans bord [Lie89, Lie91, Lie94]. Leur principal avantage est que leur définition est homogène à toutes les dimensions, contrairement aux cartes combinatoires, ce qui simplifie les définitions et l’écriture des algorithmes. De plus, cette homogénéité fait que la définition des cartes généralisées est directement valide pour les brins avec ou sans point fixe, car nous n’avons plus le problème qui se posait dans les cartes combinatoires lors de la définition des sommets. Ces cartes généralisées sont proches de la structure de cell-tuple [Bri89, Bri93].
Pour définir une carte généralisée de manière intuitive, nous appliquons le même principe de décomposition que celui utilisé pour les cartes combinatoires, mais nous effectuons une décomposition supplémentaire afin de distinguer les sommets. Si nous reprenons le premier exemple utilisé pour les cartes combinatoires présenté Fig. 2.12, nous avons obtenu au final la décomposition rappelée Fig. 2.2.4.
[a][b]
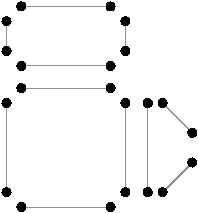
Figure 2.18: La décomposition supplémentaire d’un objet 2D pour obtenir une carte généralisée. (a) Les arêtes obtenues Fig. 2.12 après décompositions successives. (b) Les sommets de ces arêtes.
Nous décomposons ensuite les sommets, à partir de cette décomposition en arêtes et obtenons la décomposition présentée Fig. 2.2.4, où les relations d’adjacence entre les sommets d’une arête sont représentées par les segments gris. Les éléments obtenus sont les brins de la carte généralisée. Il suffit ensuite, comme pour les cartes combinatoires, de reporter les relations d’adjacence sur ces brins pour obtenir la carte généralisée présentée Fig. 2.2.4.
[a][b]
[c]
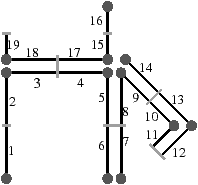
Figure 2.19: Exemple de carte généralisée 2D et convention graphique. (a) La carte combinatoire de la Fig. 2.13. (b) La carte généralisée représentant le même objet. Un brin est représenté par un segment avec un disque à une extrémité et un petit segment perpendiculaire à l’autre extrémité. Deux brins reliés par α0 sont dessinés de manière consécutive, alignés, et partagent le même petit segment perpendiculaire (par exemple α0(1)=2). Deux brins reliés par α1 partagent le même disque (par exemple α1(1)=6). Deux brins reliés par α2 sont dessinés de manière parallèle et partagent le même petit segment perpendiculaire (par exemple α2(1)=4). (c) Une 2G-carte ouverte (0-ouverte, 1-ouverte et 2-ouverte). Les brins 11, 12 et 19 sont 0-libres, les brins 1, 6, 7, 14 et 16 sont 1-libres et les brins 1, 2, 15, 16 et 19 sont 2-libres.
Étant donné que nous avons également séparé les sommets pour les cartes généralisées, nous n’avons plus besoin, comme pour les cartes combinatoires, d’utiliser une permutation pour parcourir les faces. En effet, chaque «côté» d’une arête sera lié avec l’arête suivante de la face pour ce sommet. Il existe donc une involution α0 qui met en relation les deux brins de la même face et de la même arête, une involution α1 qui met en relation les deux brins de la même face et du même sommet, et une involution α2 qui met en relation les deux brins de la même arête et du même sommet.
Comme pour les cartes combinatoires, nous ne représentons pas de manière explicite toutes les involutions et utilisons la représentation intuitive présentée Fig. 2.2.4. Deux brins cousus par α0 sont représentés par un seul segment portant un petit segment perpendiculaire en son milieu, deux brins cousus par α1 sont représentés de manière contiguë séparés par un disque, et deux brins cousus par α2 sont représentés parallèles et proches, avec la barre représentant α0 traversant les deux segments.
Nous pouvons voir Fig. 2.20 le même principe appliqué en dimension 3 à notre exemple de la Fig. 2.14. Pour les cartes combinatoires, nous avons obtenu au final la décomposition en arêtes rappelée Fig. 2.2.4.
[a][b]
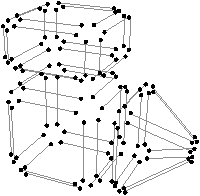
Figure 2.20: La décomposition supplémentaire d’un objet 3D pour obtenir la carte généralisée correspondante. (a) Les arêtes obtenues Fig. 2.14 après décompositions successives. (b) Les sommets de ces arêtes.
La décomposition en sommets des arêtes de cette figure est présentée Fig. 2.2.4, et la carte généralisée correspondante Fig. 2.2.4.
[a][b]
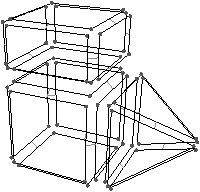
Figure 2.21: Exemple de carte généralisée 3D et convention graphique. (a) La carte combinatoire de la Fig. 2.15. (b) La carte généralisée représentant le même objet. La convention graphique utilisée est la même qu’en 2D. Généralement α3 n’est pas représenté car il peut se retrouver sans ambiguïté par la forme des faces.
La Def. 27 [Lie91] donne la définition des cartes généralisées en dimension n :
En comparaison avec les cartes combinatoires, il existe une involution supplémentaire, et il n’y a plus de différence entre les α qui sont tous des involutions. De plus, ces involutions peuvent maintenant toutes être avec ou sans point fixe sans que cela change la définition ni que cela pose de problème pour la définition des cellules. Les nG-cartes sont définies à partir de n=−1, afin de pouvoir définir la G-carte vide, composée uniquement d’un ensemble de brins sans aucune involution. Nous parlons de brin i-libre pour un brin b point fixe pour αi (c-à-d tel que αi(b)=b). C’est un brin n’ayant pas d’autre brin en relation par αi, et qui est alors considéré comme n’ayant pas de successeur pour αi et non pas comme étant son propre successeur. De manière similaire à la notation βij, nous notons αij=αj ∘ αj.
Nous disons qu’une G-carte est i-fermée si aucun de ses brins n’est i-libre. Une carte n’étant pas i-fermée est dite i-ouverte. Enfin, nous parlons de G-carte fermée pour une G-carte i-fermée pour toutes les dimensions de l’espace, et de G-carte ouverte sinon (par exemple la 2G-carte de la Fig. 2.2.4 est fermée, et celle de la Fig. 2.2.4 est ouverte).
Les G-cartes sont totalement homogènes, ce qui simplifie les définitions et les algorithmes comme nous pouvons le voir, par exemple, pour la Def. 28 des cellules. Comme pour les cartes combinatoires, nous utilisons la notation ⟨h(αi1,…,αik)⟩ pour l’orbite contenant toutes les involutions possibles sauf celles-là, c-à-d ⟨{α0,…,αn}∖{αi1,…,αik}⟩, ainsi que la notation ensembliste ⟨h(I)⟩, avec I={αi1,…,αik}, pour l’orbite ⟨h(αi1,…,αik)⟩.
Cette définition de cellule est maintenant homogène pour toutes les dimensions i∈{0,…,n} : il n’est plus nécessaire de distinguer les sommets des autres cellules. De ce fait, le cas des points fixes ne pose plus de problème car la définition des cellules n’utilise jamais la composition de deux involutions, ce qui était la raison du problème pour la définition des sommets comme nous l’avons vu dans la section précédente.
Les définitions d’incidence et d’adjacence données pour les cartes combinatoires (Defs. 20 et 21) sont toujours valides pour les G-cartes car elles se basent sur la notion de cellule, notion que nous venons de redéfinir pour les G-cartes. Les Defs. 22 et 25 de chemin et d’isomorphisme sont identiques pour les G-cartes, sous réserve de remplacer βi par αi, la Def. 23 de connexité est toujours valide car elle utilise la notion de chemin, tandis que pour la seconde définition de connexité (Def. 24), il faut remplacer l’orbite utilisée par ⟨α0,…,αn⟩(b)=B.
Mais pour représenter des quasi-variétés orientables, les G-cartes sont deux fois plus coûteuses en espace mémoire que les cartes combinatoires. Ce surcoût en mémoire peut être prohibitif, et c’est pour cette raison que selon les applications, nous utilisons les cartes combinatoires ou les cartes généralisées, pour privilégier la généricité des opérations ou l’espace mémoire.
En effet, lorsque nous travaillons avec des G-cartes orientables, les deux modèles sont équivalents : nous savons effectuer facilement la transformation permettant de passer aux cartes combinatoires, et lorsque nous travaillons avec une carte combinatoire, nous pouvons définir sans problème la carte généralisée correspondante. Afin de réaliser cette conversion, nous devons être en mesure de savoir si une G-carte est orientable ou non. C’est l’objet de la Def. 29 donnée initialement dans [Lie94], mais que nous modifions ici pour se restreindre aux nG-cartes sans point fixe pour αi∘α0, ∀ i: 2≤ i≤ n.
Nous ajoutons la contrainte sur l’absence de point fixe pour αi∘α0, ∀ i: 2≤ i≤ n, pour garantir que HG soit une carte combinatoire valide au sens de notre Def. 17, c’est à dire sans point fixe pour βi, ∀ i: 2≤ i≤ n. Cette contrainte n’était pas présente dans la définition de [Lie94] car l’auteur utilisait la définition étendue des cartes combinatoires ayant éventuellement des points fixes (il faut également noter que, dans ce même article, la définition à été étendue aux G-cartes pouvant avoir des points fixes pour αn). Cette restriction n’est pas limitante car elle interdit uniquement des configurations très particulières dans lesquelles un brin b est lié avec b′ à la fois par α0 et par un autre αi. De ce fait, nous avons une arête repliée auquel il est très difficile d’associer un sens dans le complexe cellulaire correspondant.
Cette définition permet facilement de tester, étant donné une G-carte, si elle est orientable ou non. De manière intuitive, une G-carte orientable contient les deux orientations possibles de la carte combinatoire correspondante (cf. l’exemple de la Fig. 2.2.4)). Cette définition est valable uniquement pour les G-cartes fermées connexes pour la même raison qui pose problème lors de la définition des sommets dans les cartes combinatoires ouvertes. En effet, nous composons ici deux involutions αi∘α0, ce qui va poser problème par exemple si α0 a un point fixe b car nous allons alors avoir α0i(b)=αi(b) (cf. l’exemple de la Fig. 2.2.4). Par contre, cette définition s’étend directement aux G-cartes fermées non connexes : une nG-carte fermée est orientable si chaque composante connexe est orientable.
[a][b]
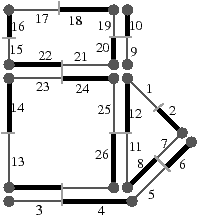
Figure 2.22: Orientation des cartes généralisées. (a) Une G-carte fermée orientable. Les brins en gras appartiennent à la même composante connexe de la n-carte HG=(B,α01,…,α0n). (b) Si la G-carte est ouverte, la n-carte HG à une seule composante connexe même lorsqu’elle est orientable. En effet, dès qu’un brin est i-libre pour n’importe quel i: 0≤ i ≤ n (par exemple le brin 1 qui est 2-libre), il existe un α0i qui va donner un brin de la seconde orientation de la G-carte (par exemple α02(1)=2 alors que les brins 1 et 2 appartiennent à deux orientations différentes de la G-carte).
La conversion entre une carte combinatoire et une carte généralisée peut s’effectuer sans contrainte, étant donné que le domaine de modélisation des cartes généralisées inclut celui des cartes combinatoires.
De manière informelle, pour convertir une carte en G-carte, nous «coupons» chaque brin bi de C en deux brins bi et ci. Nous pouvons voir Fig. 2.23 un exemple de conversion d’une carte en G-carte.
[a][b]
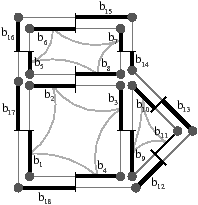
Figure 2.23: Un exemple de conversion de carte en G-carte. (a) Une carte combinatoire 2D. (b) La carte généralisée correspondante.
Chaque brin bi de la carte reste, dans la G-carte, le brin incident à la même face, à la même arête et au même sommet. Le brin de la même face, de la même arête et du sommet opposé est ci, qui est donc 0-cousu à bi. La définition des involutions de la G-carte se fait ensuite sans difficulté, en différenciant à chaque fois deux cas, suivant que le brin concerné est un brin de la carte, donc possédant des β coutures, ou un nouveau brin. De plus, il faut différencier la définition de α1 de la définition des autres α, du fait que les cartes ne sont pas homogènes.
La transformation inverse se fait de manière directe, étant donné que nous pouvons définir chaque β comme une composition de certains α. Mais pour cela, il faut nécessairement que la G-carte soit orientable. En effet, si elle ne l’est pas, il n’existe pas de carte représentant la même subdivision de l’espace. De plus, cette transformation est, comme la définition de G-carte orientable, valable uniquement pour les G-cartes connexes, fermées, et telles que ∀ i: 2≤ i≤ n, αi∘α0 soit sans point fixe. La carte combinatoire obtenue correspond à une composante connexe de la carte des orientations, c’est à dire à une orientation de la G-carte.
La carte C est définie en conservant un brin sur deux de la G-carte. En effet, comme nous savons que la G-carte est orientable et fermée, l’orbite ⟨α01,…,α0n⟩(b) va contenir un brin sur deux de la G-carte, ce qui n’est pas le cas sinon. La définition des différentes applications β sur cet ensemble de brins se fait directement : chaque βi étant simplement la composition de αi avec α0. Remarquons que la carte ainsi définie représente une orientation de la G-carte. Il est possible de définir la carte représentant l’autre orientation possible, en prenant comme brin de départ pour la définition de B′, un brin n’appartenant pas à la première orientation. Il est facile de prouver que nous obtenons bien une carte combinatoire valide. Notre condition supplémentaire sur l’absence de point fixe pour βi, ∀ i: 2≤ i≤ n découle directement de la condition ∀ i: 2≤ i≤ n, αi∘α0 est sans point fixe.
Concernant la définition de la G-carte duale, nous retrouvons ici tout l’intérêt des cartes généralisées qui grâce à leur définition homogène permettent une définition plus simple que pour les cartes combinatoires :
De plus, les preuves que la duale d’une G-carte est une G-carte, et que la cellule ci(b) dans G est égale à la cellule c′(n−i)(b) dans la carte duale G′ sont directes de par la définition des G-cartes et des cellules.
Comme nous venons de le voir, les cartes combinatoires ne peuvent pas représenter des objets ouverts. Cette limitation est due à la définition des 0-cellules qui utilise la notion d’orbite pour les compositions β0i, ∀ i, 1<i ≤ n, ce qui pose problème pour les brins étant points fixes (de manière similaire au problème de définition de l’orientation d’une G-carte avec points fixes).
Afin de régler ces problèmes, les cartes combinatoires ouvertes ont été récemment définies [PABL07], permettant de représenter des subdivisions orientables avec ou sans bord. Le principe utilisé ici pour représenter les brins libres n’est pas le même que celui utilisé dans les G-cartes qui consiste à utiliser des points fixes. En effet, cela n’est pas possible pour β1 car un point fixe pour β1 représente une boucle (une arête cousue avec elle-même) et non un brin sans successeur. De ce fait, nous considérons un élément spécifique є, en plus des brins, et autorisons les brins à être mis en relation avec є pour indiquer qu’ils sont 1-libres. Nous conservons ce même principe pour les autres βi dans le but d’avoir des définitions homogènes.
De par cette définition des brins libres, la contrainte sur les βi, pour i ≠ 1, qui doivent être sans point fixe, est conservée, comme dans la Def. 17 des cartes combinatoires, et pour les mêmes raisons.
Lorsque des brins sont i-cousus avec є, βi n’est plus une permutation ou une involution sur B, mais ce que nous appelons une permutation partielle ou involution partielle car seuls les brins d’un sous-ensemble X⊆ B sont liés à des brins de B, les brins de B ∖ X étant liés à є. La définition d’une permutation partielle et de son inverse est donnée Def. 34.
Une permutation partielle f sur E peut être vue comme une bijection entre deux sous-ensembles1 F et G de E telle que les éléments de E qui n’appartiennent pas à F sont liés avec є par f, et les éléments de E qui n’appartiennent pas à G sont liés avec є par f−1. Si ∄ e ∈ E tel que f(e)=є, alors la permutation partielle f est une permutation définie sur E.
Nous montrons dans la Prop. 3 que l’inverse est «correctement défini» car l’inverse de l’inverse d’une permutation partielle est bien la permutation partielle initiale.
Proof. Nous notons g=f−1 (qui est bien une permutation partielle) et nous étudions g−1. Soit e ∈ E, il y a deux cas :
Une involution partielle (cf. Def. 35) est une permutation partielle qui vérifie, pour les brins non libres, la propriété d’une involution (c-à-d f(f(e))=e).
Comme une involution partielle est une permutation partielle, son inverse est définie. La Prop. 4 prouve qu’un involution partielle est égale à son inverse.
Proof. Soit e ∈ E. Il y a deux cas.
Nous pouvons également vérifier que la composition de deux permutations partielles vérifie les propriétés classiques de la composition:
Proof. Prouvons tout d’abord que (f ∘ g) est une permutation partielle. Soit e ∈ E. Il y a deux cas.
(1) Si g(e)=є ou f(g(e))=є, il n’y a pas de condition dans la définition d’une permutation partielle dans ce cas.
(2) Sinon, g(e)=e′≠ є et f(e′)=e″ ≠ є. Alors par Def. 34, ∄ x ≠ e, tel que g(x)=e′, et ∄ y ≠ e′, tel que f(y)=e″. Donc ∄ x ≠ e tel que (f ∘ g)(x)=e″ et donc (f ∘ g) est une permutation partielle.
Prouvons maintenant que (f ∘ g)−1 = g−1 ∘ f−1. Soit e ∈ E. Il y a deux cas selon que (f ∘ g)−1(e)=є ou non.
(1) Par définition des permutations partielles, (f ∘ g)−1(e)=є si ∄ e′ ∈ E tel que (f ∘ g)(e′)=e. Supposons maintenant que g−1 ∘ f−1(e)=e′ ≠ є. Alors il existe e″ ∈ E tel que f(e″)=e et g(e′)=e″. Dans ce cas, nous avons (f ∘ g)(e′)=e ce qui est en contradiction avec (f ∘ g)−1(e)=є. Donc (f ∘ g)−1(e)=g−1 ∘ f−1(e).
(2) Si (f ∘ g)−1(e)=e′ ≠ є. Alors par définition f ∘ g(e′)=e. Donc il existe e″ ∈ E tel que g(e′)=e″ et tel que f(e″)=e. De ce fait f−1(e)=e″ et g−1(e″)=e′. Donc (f ∘ g)−1(e)=g−1 ∘ f−1(e).
Les cartes combinatoires ouvertes peuvent maintenant être définies :
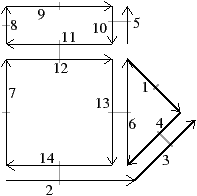
Les cartes ouvertes diffèrent des cartes sur trois points : (1) β1 est une permutation partielle et plus une permutation ; (2) les autres βi, 2 ≤ i ≤ n, sont des involutions partielles ; (3) la condition 4 est modifiée afin que βi∘βj soit une involution partielle, et cette condition doit également être testée pour β0∘βj. Un exemple de 2-carte ouverte est donné Fig. 2.24.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 β1 4 3 є 6 є 1 12 9 10 11 8 13 14 7 β2 є 14 4 3 10 13 є є є 5 12 11 6 2
Figure 2.24: Exemple de 2-carte ouverte. Les brins 3 et 5 sont 1-libres, et les brins 1, 7, 8 et 9 sont 2-libres.
Les deux premières différences proviennent directement du fait de vouloir représenter des brins libres. La troisième différence provient du fait que si β1∘βj est une involution partielle, alors β0∘βj n’est pas nécessairement une involution partielle. En effet, considérons une 3-carte composée de 3 brins : b1, b2, b3, avec β1(b2)=b1 et β3(b1)=b3 (et donc β3(b3)=b1 pour que β3 soit une involution partielle), les autres β étant tous reliés à є. Alors, pour tout brin b, nous avons β1∘β3=є donc β1∘β3 est une involution partielle. Par contre β0∘β3 n’est pas une involution partielle car β0∘β3(b3)=b2 tandis que β0∘β3(b2)=є.
Nous étudions maintenant les propriétés des cartes combinatoires ouvertes. La Prop. 3 implique directement que β0−1=β1. La Prop. 6 traite des propriétés des compositions des permutations et involutions partielles.
Proof. βi∘βj est une involution partielle par Def. 36, donc égal à son inverse (βi∘βj)−1 (par Def. 35). Étudions les 3 cas :
Nous allons maintenant utiliser cette proposition pour prouver la Prop. 7 montrant que les βj∘βi sont également des involutions partielles.
Proof. La preuve est directe en utilisant le fait que ∀ i,j: 0 ≤ i<i+2≤ j ≤ n et j ≥ 3, βi∘βj est une involution partielle par la Def. 36, et en utilisant la Prop. 6.
Le fait que βi∘βj et βj∘βi soient des involutions partielles montre la validité de la définition des cartes ouvertes pour les brins non libres puisque, pour ces brins, nous nous ramenons à l’équivalent de la définition des cartes originales. Mais nous devons également étudier l’impact de cette condition sur les brins libres. C’est ce qui est fait dans la Prop. 8 où nous prouvons que tout couple de brins (b, βi(b)) a le même «type» de voisinage pour βj (c-à-d ils sont soit tous deux j-libres, soit j-cousus).
Proof. Pour la première proposition, si b est non i-libre, soit b′=βi(b). Supposons b est j-libre et b′ non. Alors notons βj(b′)=b″, et donc βij−1(b″)=b tandis que βij−1(b)=є car b est j-libre et βj−1=βj car j≥ 3. Contradiction avec le fait que βij−1 soit une involution, donc b′ est j-libre. De manière symétrique, supposons b non j-libre et b′ j-libre. Alors notons βj(b)=b″, et donc βji(b″)=b′ alors que βji(b′)=є car b′ est j-libre. Contradiction avec βji est une involution, donc b′ n’est pas j-libre.
Pour la seconde proposition, nous effectuons une démonstration similaire avec b et b′=βj(b). Comme nous savons que βij et βji sont des involutions, et en utilisant les Props. 4 et 5 (sur l’inverse d’une involution partielle et sur l’inverse de la composition de deux permutations partielles) nous pouvons à chaque fois conclure.
Comme pour les G-cartes, nous employons les termes de carte i-fermée, i-ouverte, fermée et ouverte selon la présence ou non de brin i-libre. Dans la suite de ce manuscrit, pour alléger les écritures, nous parlerons de carte combinatoire ou carte pour désigner des cartes pouvant être ouvertes ou non, et nous préciserons si la carte est fermée lorsqu’il sera nécessaire de faire la distinction.
Nous devons maintenant modifier la notion d’orbite pour enlever l’élément є des éléments de l’orbite. En effet, dans la définition originale, l’orbite d’un brin est l’ensemble des éléments atteignables par application des permutations et de leurs inverses. Cet ensemble peut donc désormais contenir є, ce qui n’est pas correct.
Cette notion d’orbite sert, comme pour les cartes combinatoires fermées, à définir les cellules. De ce fait, la Def. 19 des i-cellules dans les cartes fermées est toujours valide pour les cartes ouvertes, pour i>1. En effet, l’orbite permet bien de récupérer tout les brins de la cellule, tout en évitant є. Par contre, nous devons modifier la définition des sommets (Def. 38 des 0-cellules), car la définition originale est incomplète à cause de la présence éventuelle de brins libres.
Par rapport à la définition originale, nous ajoutons dans l’orbite considérée les βij avec 2 ≤ i < j ≤ n pour garantir de ne pas rater de brins du fait de la présence de brins 0 ou 1-libres. Prenons l’exemple d’une 3-carte C={B,β1,β2,β3} composée de 3 brins numérotés 1,2 et 3, tel que β2(1)=2 et β3(2)=3 (et donc β2(2)=1 et β3(3)=2). Les brins 1 et 3 appartiennent au même sommet (le fait d’utiliser βi avec 2≤ i ≤ n fait changer de sommet, donc utiliser β2 puis β3 redonne le même sommet). Mais il n’existe pas de chemin allant du brin 1 au brin 3 en utilisant β02, β03 et leurs inverses β21 et β31. En effet, le brin 1 étant 0-libre, et les brins β2(1) et β3(2) étant 1-libres, la valeur de chacune de ces permutations pour le brin 1 est égale à є. Le fait d’ajouter β23 dans l’orbite sommet résout ce problème. Il faut noter que ce cas ne peut pas se produire pour les autres i-cellules, 0<i≤ n, car l’orbite n’utilise pas de composition de permutations.
Sur l’exemple de la Fig. 2.24, le sommet incident au brin 12 est {8,12}. L’arête incidente au brin 1 est <β2>(1) = {1} (car le brin 1 est 2-libre), tandis que l’arête incidente au brin 11 est <β2>(11) = {11,12}. La face incidente au brin 2 est <β1>(2) = {2,3}.
Les définitions de carte inverse, incidence, adjacence, chemin et carte connexe, données dans le cadre des cartes fermées, sont toujours valides dans le cadre des cartes ouvertes. La Def. 25 d’isomorphisme de cartes doit être modifiée uniquement pour ajouter la condition que f(є)=є.
La Def. 26 des cartes duales est toujours valide dans le cadre des cartes ouvertes, à condition que les cartes soient n-fermées. En effet, comme la définition de carte duale compose βn avec les autres β, si une carte est n-ouverte, cela peut avoir pour conséquence d’obtenir un résultat qui ne vérifie pas la condition 4 de la définition des cartes.
Prenons comme exemple une 3-carte C=(B,β1,β2,β3) composée de 3 brins numérotés 1, 2 et 3, et tel que β2(1)=2 et β3(1)=3 (donc β2(2)=1 et β3(3)=1), tous les autres β donnant є. Cette carte vérifie bien la condition 4 de la définition des cartes ouvertes (qui en 3D est que β13 est une involution partielle). La carte duale de cette carte est C=(B,β1′,β2′,β3′)=(B,β32,β31,β3). Nous avons donc β3′(1)=β3(1)=3, β1′(3)=β32(3)=2 et β3′(3)=β3(3)=1, tous les autres β donnant є. Ce n’est donc pas une carte combinatoire car β03′ n’est pas une involution partielle (car β03′(2)=1 et β03′(1)=є).
En ajoutant un brin 4 à la carte C tel que β3(2)=4 (et donc β3(4)=2) sans changer les β des autres brins, la carte C est maintenant 3-fermée. Pour la carte duale C=(B,β1′,β2′,β3′)=(B,β32,β31,β3), nous avons maintenant β1′(3)=2, β1′(4)=1, β3′(1)=3, β3′(2)=4, β3′(3)=1, et β3′(4)=2, tous les autres β étant liés à є. C est ici une 3-carte : β03′ est bien une involution partielle (β03′(1)=2 ; β03′(2)=1 ; β03′(3)=є et β03′(4)=є).
Les preuves faites par rapport aux cartes duales dans le cadre des cartes fermées sont similaires, mais elles doivent être légèrement modifiées car la composition d’une involution partielle avec elle-même n’est plus l’identité (c’est l’identité seulement pour les brins non libres), et cela est utilisé souvent dans les démonstrations. Mais résoudre ce problème se fait simplement en distinguant à chaque fois les cas des brins reliés à є des autres cas. C’est le cas pour la Prop. 1 disant que la duale d’une carte est une carte, et pour la Prop. 2 qui prouve qu’une i-cellule incidente à b dans une carte est égale à la (n−i)-cellule incidente à b dans la carte duale. Il faut noter que comme la carte est désormais ouverte, lorsqu’une i-cellule est ouverte (un de ses brins est libre pour un βj, j≠ i) dans la carte initiale, la (n−i)-cellule correspondante est également ouverte dans la carte duale.
Nous présentons un exemple de carte ouverte duale Fig. 2.25. Sur cet exemple, la 2-carte est ouverte mais 2-fermée. Nous pouvons voir par exemple que β1′(5)=β21(5)=7, tandis que β1′(1)=є car β21(1)=є. Nous pouvons également vérifier sur cet exemple que les i-cellules de la carte de la Fig. 2.2.5 se transforment bien en (2−i)-cellules dans la carte de la Fig. 2.2.5. Par exemple la 0-cellule c0(5)={5,7,9} de la carte initiale se transforme bien en la 2-cellule c′2(5) dans la carte duale ; la 1-cellule c1(5)={1,5} de la carte initiale se transforme bien en la 1-cellule c′1(5) dans la carte duale ; et la 2-cellule c2(8)={8,9,10} de la carte initiale se transforme bien en la 0-cellule c′0(8) dans la carte duale.
[a][b]
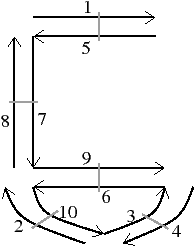
Figure 2.25: Exemple de duale d’une carte combinatoire ouverte. (a) Une 2-carte combinatoire ouverte, mais 2-fermée. (b) La 2-carte combinatoire duale.
Le problème évoqué ci-dessus de non-validité de la carte duale d’une carte n-ouverte ne se pose pas dans ces termes pour n≤ 2. En effet, pour ces cartes, la condition 4 ne s’applique pas, et donc n’importe quel ensemble de brins, avec n’importe quelles applications β, est une carte combinatoire valide en 0, 1 et 2D. Mais par contre, comme nous pouvons voir Fig. 2.26, le problème qui se pose alors est qu’il peut ne plus y avoir de correspondance entre les i-cellules de la carte et les (n−i)-cellules de la carte duale. Par exemple la face c2(8)={8,9,10,11} de la carte de la Fig. 2.2.5 est éclatée dans les deux sommets c′0(8)={8,10,11} et c′0(9)={9} dans la carte duale de la Fig. 2.2.5. De ce fait, la contrainte sur la carte qui doit être n-fermée est nécessaire pour tout n, y compris n≤ 2.
[a][b]
Figure 2.26: Exemple de problème pour la duale d’une carte combinatoire 2-ouverte. (a) Une 2-carte combinatoire 2-ouverte. (b) La 2-carte combinatoire duale correspondante. C’est une carte combinatoire valide, mais il n’y a pas correspondance entre les i-cellules de la première carte et les (n−i)-cellules de la carte duale (par exemple la face c2(8)={8,9,10,11} est éclatée dans les deux sommets c′0(8)={8,10,11} et c′0(9)={9}.
Comme nous venons d’introduire les cartes combinatoires ouvertes, nous pouvons maintenant re-considérer le problème de conversion entre carte et G-carte. En effet, la définition initiale imposait que la G-carte soit fermée afin que la carte combinatoire le soit également. Mais cette contrainte n’est désormais plus nécessaire. Mais pour supprimer cette contrainte, nous devons au préalable étendre la Def. 29 permettant de tester si une G-carte est orientable aux G-carte ouvertes, car cette définition est utilisée dans la définition de la conversion.
Pour cela, nous devons considérer différemment les brins points fixes de la G-carte des autres brins. Pour cela, nous définissons la conversion d’une involution en involution partielle sans point fixe, qui va transformer la convention utilisée pour les brins libres dans les G-cartes (c-à-d les brins points fixes) en la convention utilisée pour les brins libres dans les cartes ouvertes (c-à-d les brins liés à є).
Il est facile de prouver que si f est une involution sur E, alors f• est une involution partielle. Nous pouvons également remarquer que l’involution partielle f• est sans point fixe car tous les points fixes de f ont été transformés en éléments en relation avec є. Nous pouvons maintenant utiliser cette transformation pour re-définir la notion de G-carte orientable dans la Def. 40.
L’utilisation de la composition avec point fixe nous permet d’avoir la même définition que dans le cas des G-cartes fermées, après avoir transformé les involutions en involutions partielles. Cette définition semble montrer que si les cartes généralisées étaient définies de manière similaire aux cartes combinatoires ouvertes, avec des involutions partielles et є pour les points fixes, certaines définitions pourraient être plus simples. Il pourrait être intéressant d’étudier plus précisément cette possibilité en comparant les deux approches de manière approfondie.
La contrainte sur la nG-carte qui doit être 0-fermée est nécessaire afin de s’assurer que pour toute G-carte connexe, HG soit bien composée de deux composante connexes. En effet, sans cette contrainte, la G-carte peut-être composée de plusieurs parties reliées par des brins 0-libres. Dans ce cas, il ne sera pas possible de «passer» à travers ces brins car tous les αi•∘α0 vont donner є. De ce fait, le nombre de composantes connexes de HG ne serait plus lié à l’orientabilité de G. Prenons par exemple la 2G-carte G=(B,α0,α1,α2) composée de trois brins numérotés 1, 2 et 3, et tel que α2(1)=2, α1(2)=3 (et donc α2(2)=1, α1(3)=2) les autres relations étant libres. Cette G-carte est clairement orientable, et pourtant HG est composée de trois composantes connexes car chaque brin de HG est totalement isolé.
La n-carte HG est une carte combinatoire. En effet, nous savons que la composition de deux permutations partielles est une permutation partielle, et il est facile de prouver que les αi•∘ α0, pour 2≤ i≤ n, sont des involutions partielles sans point fixe (en utilisant la propriété des G-cartes disant que les αi ∘ α0 sont des involutions, le fait que α0 soit sans point fixe, et la contrainte sur les αi∘α0 qui sont sans point fixe).
Les deux définitions de G-carte orientable sont équivalentes dans le cas d’une G-carte fermée puisqu’il n’y a alors aucun brin b qui soit point fixe, et donc les αi• sont tous égaux aux αi. Par contre, pour une G-carte ouverte, le fait de transformer les involutions en involutions partielles modifie la liaison des brins libres qui sont maintenant reliés à є. De ce fait, la composition αi•∘ α0 pour ce type de brin sera égale à є (car є est lié avec lui même pour chaque involution partielle) et contrairement à précédemment nous n’obtenons pas un brin appartenant à l’orientation inverse.
La conversion de G-carte en carte s’étend maintenant directement pour les cartes ouvertes (cf. Def. 41), en utilisant à nouveau la conversion entre les involutions et les involutions partielles.
De manière informelle, pour convertir une G-carte G en carte, nous prenons seulement les brins de G appartenant à la même orientation et relions ces brins par les βi correspondant aux α0i. Nous pouvons voir Fig. 2.27 un exemple de conversion d’une G-carte en carte.
[a][b]
Figure 2.27: Un exemple de conversion de G-carte en carte. (a) Une carte généralisée 2D. (b) La carte combinatoire correspondante.
Nous pouvons vérifier sur cet exemple que la conversion est correctement effectuée pour les brins 1-libres et pour les brins 2-libres (les brins 0-libres étant interdits par définition, et pour les brins non libres la définition se ramène à la définition originale). Par exemple, α0(b10) est 1-libre, nous avons donc α1•∘ α0(b1)=є et donc β1(b10)=є ; α0(b1) est 2-libre, nous avons donc α2•∘ α0(b1)=є et donc β2(b1)=є.
Pour définir la conversion d’une carte en G-carte (cf. Def. 42), nous ne pouvons pas utiliser un principe similaire à celui utilisé pour la conversion de G-carte en carte qui consisterait à transformer une permutation partielle en permutation, car nous devons différencier les brins libres des autres. À part cette distinction, le principe de cette conversion est identique à la définition correspondante dans le cadre des cartes fermées.
| bi | si bi est 0-libre |
| α0(β0(bi)) | sinon |
| ci | si bi est 1-libre |
| β1(bi) | sinon |
| ∀ j: 2 ≤ j ≤ n : |
| |||||||
| ||||||||
Pour un brin bi non j-libre (1≤ j ≤ n), cette définition est identique à la définition initiale. Pour un brin bi j-libre, nous ne pouvons pas utiliser une conversion de la permutation partielle en permutation, car le résultat de cette conversion serait bi, et comme nous utilisons ensuite α0 nous obtiendrions αj(bi)=ci alors que nous devons avoir αj(bi)=bi. Pour éviter ce problème, nous testons simplement si le brin bi est j-libre et fixons dans ce cas les α correspondants de bi et de ci à bi et ci, ce qui indique que ces brins sont libres.
Pour illustrer cette transformation, il suffit de regarder l’exemple de la Fig. 2.27 dans l’autre sens : la carte combinatoire de départ est celle de la Fig. 2.2.5 et le résultat de la transformation est la G-carte de la Fig. 2.2.5. Nous pouvons vérifier sur cet exemple que la transformation est correcte pour les brins libres (le cas des brins non libres se ramène à la définition originale). Par exemple, b8 est 0-libre, nous avons donc α1(b8)=b8 ; b10 est 1-libre, et nous avons donc α1(c10)=c10 (avec c10=α0(b10)) ; et b1 est 2-libre, et donc α2(b1)=b1 et α2(c1)=c1 (avec c1=α0(b1)).
Comme n’importe quelle carte combinatoire ouverte peut être convertie en carte généralisée, et comme une G-carte représente une quasi-variété, cela prouve directement que n’importe quelle carte combinatoire ouverte correspond également à une quasi-variété. De plus, ces méthodes de conversion nous permettent, dans la suite de cette présentation, de travailler indifféremment avec une carte combinatoire ou une carte généralisée orientable. Cela nous permettra, par exemple, de travailler avec des G-cartes pour définir les opérations de base en dimension quelconque, afin de profiter de leur homogénéité, puis de travailler avec des cartes combinatoires pour définir les modèles de représentation d’images qui ont des contraintes d’espace mémoire.
Les cartes combinatoires et les cartes généralisées représentent seulement la topologie des objets, c’est-à-dire les cellules et les relations d’incidence et d’adjacence. Mais la plupart des applications ont besoin également de représenter la géométrie de ces objets, par exemple pour les afficher, pour calculer des caractéristiques de forme, de taille…Il nous faut donc associer un modèle géométrique aux cartes. Pour cela, nous pouvons associer un élément géométrique de dimension i à chaque i-cellule de la carte. Nous appelons plonger l’opération qui consiste à associer un modèle géométrique à un modèle topologique, et nous parlons du plongement d’un modèle topologique pour désigner le modèle géométrique associé.
Par exemple, en dimension 2, nous pouvons associer à chaque sommet topologique (0-cellule) un point de ℝ2. Ce plongement peut suffire pour représenter totalement la géométrie des objets ayant un plongement linéaire, c’est-à-dire tels que chaque arête corresponde à un segment de droite, chaque face soit une portion d’un plan…. Dans ce cas, le plongement de toutes les i-cellules, ∀ i: 1≤ i ≤ n, est implicite et se déduit à partir du plongement des sommets.
Si le plongement n’est pas linéaire, le plongement des sommets ne suffit pas pour déduire le plongement des autres cellules. Nous devons alors plonger chaque i-cellule topologique dans un objet géométrique ouvert de dimension i. Cet objet doit être ouvert, car le plongement du bord de la i-cellule topologique est représenté par le plongement de ses (i−1)-cellules incidentes. Il faut également satisfaire à des contraintes d’incidence pour que le plongement soit cohérent avec le modèle combinatoire (par exemple une contrainte liant le plongement d’un sommet avec l’extrémité du plongement des arêtes incidente à ce sommet). Pour cette même raison, les plongements ne doivent pas avoir d’intersections (en dehors de leurs bords) car nous n’avons alors plus de lien entre la partition du modèle combinatoire, et la partition géométrique donnée par le plongement.
Cette distinction topologie/géométrie est un des points fort des cartes. En effet, selon les algorithmes, nous allons pouvoir effectuer certains traitements en utilisant uniquement la topologie, en oubliant la géométrie correspondante (comme par exemple le calcul de propriétés topologiques comme la caractéristique d’Euler-Poincaré), et à l’inverse effectuer des traitements portant uniquement sur la géométrie, sans modifier la carte (comme par exemple la translation d’un objet). Même dans le cas d’un algorithme «mixte» travaillant à la fois sur la topologie et la géométrie, cette séparation va simplifier les accès aux informations et les modifications.
Le lien entre les cartes (combinatoires et généralisées) et les ensembles semi-simpliciaux est important car il permet de faire des rapprochements avec les nombreux travaux de topologie algébrique basés sur les complexes simpliciaux, et il permet de donner une interprétation topologique aux cartes. En effet, les ensembles (semi)-simpliciaux ont été beaucoup étudiés, et leurs propriétés topologiques sont bien connues. Ce lien permet par exemple, comme illustré dans la Section 2.3.3, d’utiliser cette conversion pour définir la caractéristique d’Euler-Poincaré des cartes (combinatoires et généralisées).
L’association entre carte généralisée et ensemble semi-simplicial est définie dans [Lie94] de la manière suivante.
Chaque brin est associé à un n-simplexe (cas où i=n ce qui implique I={α0,…,αn}). Deux brins b1 et b2 en relation par αj (0 ≤ j ≤ n) correspondent à deux n-simplexes s1=φn(b1) et s2=φn(b2) qui sont adjacents et partagent un (n−1)-simplexe s tel que djn(s1)=s et djn(s2)=s. En effet, la seconde condition pour i=n indique que ∀ j : 0≤ j≤ n, djn(φn(b1))=φn−1(⟨αj⟩(b1)) et que djn(φn(b2))=φn−1(⟨αj⟩(b2)). Comme b1=αj(b2), alors ⟨αj⟩(b1)=⟨αj⟩(b2) et donc djn(φn(b1))=djn(φn(b2)). De ce fait, chaque opérateur de face djn correspond à αj. Il est prouvé dans [Lie94] que K est bien un ensemble semi-simplicial en montrant que les opérateurs de face vérifient bien les contraintes nécessaires.
Nous montrons Fig. 2.28 un exemple de conversion de 2G-carte en ensemble semi-simplicial. Nous voyons sur cet exemple que les opérateurs de face di2 sont l’analogue des αi pour la G-carte. En 2D, les 0-simplexes correspondent aux orbites ⟨α0,α1⟩, ⟨α0,α2⟩, et ⟨α1,α2⟩ (par exemple le 0-simplexe a correspond à l’orbite ⟨α1,α2⟩(21)={21,24,26,27}, b correspond à l’orbite ⟨α0,α2⟩(26)={25,26,27,28} et c correspond à l’orbite ⟨α0,α1⟩(21)={15,16,17,18,21,22,25,26}), les 1-simplexes aux orbites ⟨α0⟩, ⟨α1⟩ et ⟨α2⟩ (par exemple le 1-simplexe [ab] correspond à l’orbite ⟨α2⟩(26)={26,27}, [ac] correspond à l’orbite ⟨α1⟩(21)={21,26}, et [bc] correspond à l’orbite ⟨α0⟩(25)={25,26}), et les 2-simplexes aux orbites ⟨⟩ (c-à-d aux brins).
[a][b]
Figure 2.28: Conversion d’une carte généralisée en un ensemble semi-simplicial. (a) Une carte généralisée 2D. (b) L’ensemble semi-simplicial correspondant. Chaque 2-simplexe est numéroté avec le numéro du brin correspondant. Trois 0-simplexes sont nommés a,b et c. Les opérateurs de face sur les 2-simplexes sont représentées par les flèches grises avec un numéro indiquant le i de l’opérateur de face di2.
Nous pouvons vérifier sur un second exemple, présenté Fig. 2.29, que la conversion est toujours valide pour les G-cartes ouvertes sans avoir de cas particulier ni de différence avec le cas des G-cartes fermées. C’est dû à la définition des orbites qui «fonctionne» de manière identique dans le cas des G-cartes fermées et ouvertes.
L’association entre carte combinatoire et ensemble semi-simplicial est définie dans [Lie94] en se basant sur la conversion des G-cartes en ESS, puis en utilisant le lien entre les G-cartes et les cartes. Comme nous avons étendu ici cette conversion à toute carte combinatoire ouverte ou non, nous obtenons directement l’association entre chaque carte combinatoire et un ensemble semi-simplicial correspondant. Il faut noter que comme nous passons par la conversion d’une carte en G-carte, chaque brin de la carte se retrouve associé à deux brins de la G-carte et donc à deux n-simplexes dans l’ensemble semi-simplicial. Nous montrons un premier exemple de ce type de conversion dans la Fig. 2.30.
Nous pouvons voir Fig. 2.31 un exemple de conversion de 2-carte ouverte en ensemble semi-simplicial. Nous pouvons effectuer les mêmes vérifications sur cet exemple par rapport aux liens entre les orbites et les simplexes que pour l’exemple de 2-carte fermée.
Ce principe de conversion à l’avantage d’être simple car il réutilise les travaux sur les G-cartes, mais possède comme inconvénient d’associer deux n-simplexes à chaque brin de la carte ce qui n’est pas naturel. De plus, cela rend plus difficile sa présentation car il faut nécessairement introduire les G-cartes avant de présenter cette conversion. Pour ces raisons, nous avons commencé à étudier une définition de conversion directe qui associerait un seul n-simplexe par brin de la carte. Mais cette définition semble complexe et ce travail n’a pour le moment pas encore abouti.
L’utilisation de la conversion entre les cartes (combinatoires ou généralisées) et les ensembles semi-simpliciaux nous fournit directement une manière de calculer la caractéristique d’Euler-Poincaré. En effet, la Def. 13 indique que cette caractéristique est la somme alternée du nombre de cellules de la subdivision, et l’ensemble semi-simplicial nous fournit directement le nombre de chaque i-cellule en comptant le nombre de i-simplexes.
De ce fait, que ce soit pour les cartes combinatoires ouvertes ou non, ou pour les cartes généralisées, la caractéristique d’Euler correspondante se calcule simplement en effectuant la somme alternée du nombre de simplexes de l’ensemble semi-simplicial correspondant. Nous donnons Def. 44 la définition de la caractéristique d’Euler-Poincaré d’une G-carte. Pour les cartes, il faudra préalablement passer par la phase de conversion en G-carte, puis utiliser la même définition.
| χ(G)= |
|
| (−1)iz(⟨h(αk0,…,αki)⟩). |
Cette formule est la somme alternée, pour i allant de 0 à n, du nombre de i-simplexes de l’ensemble semi-simplicial correspondant à la G-carte. Pour l’exemple de la Fig. 2.28, cette formule nous donne χ=(z(⟨α0,α1⟩)+z(⟨α0,α2⟩)+ z(⟨α1,α2⟩))−(z(⟨α0⟩)+z(⟨α1⟩)+z(⟨α2⟩))+ (z(⟨⟩)), donc χ=(4+9+7)−(18+18+18)+(36). Nous obtenons donc χ=2 : c’est la caractéristique d’Euler-Poincaré de la sphère, qui correspond bien à la subdivision représentée par la carte de la Fig. 2.3.1.
Une autre manière de calculer la caractéristique d’Euler-Poincaré d’une carte consiste à effectuer directement la somme alternée du nombre de cellules de la subdivision (cf. Def. 45 et [Lie94]).
| χc(G)= |
| (−1)iz(⟨h(αi)⟩). |
Nous notons cette deuxième version χc(G) pour caractéristique d’Euler-Poincaré cellulaire, en opposition avec la première définition qui peut-être vue comme la caractéristique d’Euler-Poincaré simpliciale, car elle utilise implicitement la conversion de G-carte en ensemble semi-simplicial.
Les deux caractéristiques sont équivalentes lorsque les trois conditions suivantes sont vérifiées [Lie94] :
Ces conditions sont nécessaires pour éviter des cas particuliers (par exemple de repliement) posant problème lors du calcul du nombre de cellules. Intuitivement, ces conditions reviennent à garantir que la G-carte représente bien un complexe cellulaire valide dans lequel il est possible d’utiliser la définition originale de la caractéristiques d’Euler-Poincaré (cf. Def. 13). La première condition évite les G-cartes ouvertes car dans ce cas il faudrait intégrer le nombre de bords au calcul. La seconde condition revient à éviter des repliements (par exemple en 3D, pour i=2, cette condition devient α2(b)∉ ⟨α0(b)⟩ ce qui revient à replier une arête sur elle-même. Cela pose un problème car nous avons alors une sorte de demi-arête qui est difficile à intégrer dans les nombres de cellules)). La troisième condition revient à imposer à chaque i-cellule d’avoir la même caractéristique d’Euler-Poincaré qu’une boule Bi (il faut noter que χ(C0)=0 pour toute composante d’une 0G-carte fermée, et que χ(C1)=2 pour toute composante d’une 1G-carte fermée). Ces explications sont pour le moment uniquement intuitives et ce travail doit être approfondi afin d’étudier plus précisément les conséquences de ces conditions. Il faut noter que la deuxième condition inclut notre condition supplémentaire pour la conversion de G-carte en carte (condition liée à l’interdiction de point fixe dans les cartes). C’est une raison supplémentaire indiquant que notre nouvelle condition n’est pas limitante.
Pour l’exemple de la Fig. 2.28, les trois conditions sont satisfaites et les deux définitions sont donc équivalentes. Nous avons χc(G)=7−9+4=2 (sommets-arêtes+faces) et nous avons bien χc(G)=χ(G). Par contre, dans le cas présenté Fig. 2.29, nous avons χ(G)=21−48+28=1, alors que χc(G)=7−9+5=3. Les deux caractéristiques ne sont pas égales car la G-carte n’est pas fermée. De ce fait la caractéristique cellulaire n’est ici pas valide.
L’avantage de cette seconde définition est que le nombre d’orbites à calculer est moindre que dans le premier cas (par exemple en 2D nous avons trois orbites à calculer au lieu de sept dans le cas simplicial). Il serait intéressant d’étudier plus en détail ces conditions pour mieux comprendre le lien entre les G-cartes les vérifiant et les complexes cellulaires. Cela amènerait peut-être à la définition d’une sous-catégorie de cartes qui auraient alors de «bonnes propriétés». En effet, les cellules non homéomorphes à des boules sont souvent la cause de problèmes, et définir cette catégorie de G-cartes serait intéressant car cela garantirait de les éviter. Il en est de même pour les repliements.
Dans ce chapitre nous avons tout d’abord présenté les notions de base de topologie algébrique qui vont servir durant tout ce mémoire, ce qui nous a permis d’introduire les complexes simpliciaux et cellulaires. Nous avons ensuite présenté les modèles combinatoires permettant de représenter ces notions abstraites : ils sont au cœur de nos travaux et nous avons donc détaillé les cartes combinatoires et les cartes généralisées en présentant la plupart des notions existantes et en montrant de manière précise le lien entre ces modèles et les ensembles semi-simpliciaux.
L’apport principal de ce chapitre est de regrouper en un même point la majeure partie des notions existantes autour des cartes. Nous avons essayé également d’éclaircir certaines de ces notions, soit en les illustrant, soit en détaillant certaines preuves. Nous avons également profité de ce chapitre pour présenter en détail les cartes combinatoires ouvertes et les notions associées. Cela nous a amené à revisiter légèrement les cartes combinatoires en ajoutant la contrainte sur les βi sans point fixe. De notre point de vue, cette contrainte est peu limitante car elle interdit uniquement des cas très particuliers, mais clarifie et homogénéise les relations entre les trois modèles à base de carte. De plus, nous avons présenté de manière détaillée les cartes combinatoires ouvertes qui généralisent les cartes combinatoires en autorisant les bords. De ce fait, cette notion devrait remplacer la notion précédente de carte combinatoire.
Nous aurions pu également parler des chaînes de cartes [EL93, EL94] qui permettent de représenter des complexes cellulaires quelconques, c’est-à-dire des objets dont chaque cellule est une quasi-variété, mais dont l’assemblage de ces cellules est quelconque, mais nous ne l’avons pas fait afin de ne pas alourdir encore plus ce chapitre, sachant que nous n’utilisons pas ces chaînes de cartes dans la suite de ce travail.
Ce chapitre étant principalement des rappels de notions existantes, il existe peu de perspectives, mais il en existe quand même une qui est très importante et qui concerne l’étude de la caractérisation combinatoire des boules. Ce problème transparaît lors de la définition de la caractéristique d’Euler-Poincaré cellulaire pour laquelle des contraintes ont été ajoutées. Nous souhaitons étudier plus précisément ces contraintes et leurs liens avec le complexe cellulaire sous-jacent. Cette étude passe éventuellement par la définition d’une sous-classe d’objets, et par une définition précise du lien entre les modèles à base de carte et les CW-complexes. Une seconde perspective concerne le lien entre les G-cartes et les cartes ouvertes. Nous avons évoqué le problème posé par les points fixes pour les cartes, qui se pose également pour les G-cartes lorsque nous composons des involutions. Nous souhaitons donc étudier la possibilité de modifier la définition des G-cartes pour remplacer l’utilisation des points fixes par l’utilisation d’involutions partielles. Il faut pour cela comparer précisément les deux possibilités et l’impact sur l’ensemble des définitions existantes afin de mesurer les avantages et inconvénients de cette possible deuxième approche. Une dernière perspective concerne le lien direct entre les cartes combinatoires et les ensembles semi-simpliciaux. Cette définition directe simplifierait les algorithmes de calcul de caractéristiques d’Euler-Poincaré d’une carte combinatoire en évitant la phase de conversion de carte en G-carte.
Nous avons maintenant toutes les connaissances nécessaires pour définir dans le chapitre suivant les opérations de base permettant de modifier une G-carte. De plus, les différentes preuves de conversion entre les cartes combinatoires et les cartes généralisées nous permettent de donner ces définitions uniquement pour les G-cartes, en sachant qu’elles seront alors automatiquement transposables aux cartes.


