


Afin de modifier une carte, nous définissons quatre opérations de base : la suppression de cellules, et l’opération duale, la contraction [DL03, DDLA05] qui permettent de simplifier la carte en diminuant son nombre de cellules. Nous définissons également les opérations inverses : l’insertion de cellules, et l’opération duale, l’éclatement [BDSM08] qui permettent d’ajouter des cellules (cf. la Fig. 3.1 pour le lien entre ces quatre opérations). Nous définissons ces opérations sur les cartes généralisées pour profiter de leur homogénéité, mais ces définitions se transcrivent de manière directe sur les cartes combinatoires en utilisant les algorithmes de conversion présentés au chapitre 2.
Pour chaque opération, nous privilégions la généricité en définissant ces opérations en toute dimension et pour des cellules quelconques, la seule contrainte étant que l’application de l’opération préserve les contraintes des cartes. Nous introduisons pour cela la notion de cellule supprimable (resp. contractible) pour une cellule qui peut être supprimée (resp. contractée) et donner comme résultat une G-carte valide. Par contre, en fonction des applications, il est ensuite souvent nécessaire d’ajouter des contraintes supplémentaires afin de préserver des propriétés spécifiques comme par exemple la connexité. Mais ajouter ces contraintes se fait simplement en testant certaines propriétés avant d’appliquer l’opération, qui elle reste inchangée. L’avantage de cette approche est de fournir une opération générique pouvant servir dans n’importe quel cadre. De plus, le fait de ne pas ajouter de contrainte permet à l’utilisateur de l’opération de factoriser le test de validité à un ensemble d’opérations ce qui permet d’optimiser les temps de calculs. Ces opérations peuvent être vues comme l’analogue des opérateurs d’Euler (cf. Section 3.4), généralisés en dimension quelconque. Un autre avantage de nos définitions génériques est que les quatre opérations de base englobent les nombreuses opérations d’Euler existantes (il en existe 99 en 2D).
Une dernière opération de base qui est un peu différente des quatre autres est le décalage d’arêtes [Dam01, Dam08]. Elle est différente car elle ne simplifie pas la subdivision, ni ne la complexifie, mais va la modifier en préservant certaines propriétés. Son principe consiste à «faire glisser» une arête le long d’une arête voisine. De ce fait, elle peut servir à rendre supprimable une cellule qui ne l’était pas. Cette opération est également spéciale car elle n’est pas générique. En effet, elle est pour le moment limitée aux arêtes en 2D et 3D, et liée aux conditions de la définition de cellule supprimable. Il serait intéressant de généraliser cette opération à toute dimension, à toute cellules (décalage de face, de volume...), mais aussi de proposer l’opération duale en lien avec la définition de cellule contractible.
Il faut noter que les quatre opérations de base existaient déjà (définies dans [Elt94]) de manière totalement générique, c’est-à-dire sans contrainte sur les cellules utilisées dans les opérations. De ce fait, les définitions sont très complexes et difficilement exploitables en pratique. De plus, le contrôle de ces opérations est délicat, car pour respecter les contraintes des cartes, l’application d’une opération peut avoir des conséquences difficile à prévoir sur de nombreuses autres cellules. C’est pour résoudre ces problèmes que nous avons re-défini ces opérations, en nous limitant aux cellules supprimable et contractible, afin d’obtenir une opération générale beaucoup plus simple à définir et à utiliser.
Ce chapitre est organisé de la manière suivante. Nous commençons Section 3.1 par introduire les notions préliminaires utilisées lors de la définition des opérations. Puis nous définissons, Section 3.2, les opérations de suppression et de contraction, que nous généralisons ensuite pour la suppression/contraction simultanées d’un ensemble de cellules. Dans la Section 3.3, nous définissons les opérations inverses d’insertion et d’éclatement, ainsi que la généralisation pour l’insertion/éclatement simultanées d’un ensemble de cellules. Nous montrons le lien entre les opérations de suppression et contraction en 2D et les opérations d’Euler dans la Section 3.4. L’opération de décalage d’arête est définie dans la Section 3.5. Enfin, la Section 3.6 conclut ce chapitre et présente des perspectives.
Lors de la définition des opérations de base, nous allons fixer des contraintes afin de garantir la validité de la carte obtenue après application de ces opérations. Ces contraintes sont basées sur les notions de degré et de co-degré d’une i-cellule.
Remarquons que le degré d’une n-cellule n’est pas défini pour une carte de dimension n. De plus, le degré d’une i-cellule c ne peut jamais être égal à zéro, car il existe au moins un brin dans cette cellule, et donc au moins une (i+1)-cellule incidente à c. Enfin, le degré d’une (n−1)-cellule dans une carte de dimension n, est forcément égal à un ou deux, étant donné que nous représentons uniquement des quasi-variétés (et il ne peut donc pas y avoir plus de deux n-cellules incidente à une (n−1)-cellule). Par définition des cellules, le degré d’une i-cellule c est égal à |{ci+1(b)|b ∈ c}|. En effet, comme deux (i+1)-cellules sont soit disjointes, soit confondues, l’ensemble considéré contient bien les cellules distinctes incidentes à c et son cardinal est bien le degré de c.
De manière duale, nous allons nous intéresser au nombre de (i−1)-cellules distinctes incidentes à une i-cellule donnée, c’est la notion de co-degré (appelé parfois degré inférieur ou degré dual).
De manière duale par rapport au degré, le co-degré d’une 0-cellule n’est pas défini et le co-degré d’une 1-cellule (donc une arête) est forcément égal à 1 ou 2 : une arête à toujours exactement un ou deux sommets incidents. Comme pour le degré, le co-degré d’une i-cellule c est égal à |{ci−1(b)|b ∈ c}|.
Nous pouvons voir des illustrations des notions de degré et co-degré sur la Fig. 3.2. Par exemple, la face f1 est de co-degré un car elle est incidente à une seule arête, et le sommet s1 est de degré deux car il est incident à deux arêtes distinctes.
Nous allons également utiliser par la suite la notion d’arête pendante présentée Def. 48. Intuitivement, une arête est pendante si une de ses extrémités n’est pas rattachée à une autre arête, tandis que l’autre extrémité est rattachée à une autre arête. Toujours intuitivement, une arête pendante peut-être vue comme l’extrémité d’un chemin. Plus formellement, cela veut dire qu’un de ses sommets est incident uniquement à cette arête, ou dit autrement que le degré d’un de ses sommets est 1. Dans cette définition, une boucle n’est pas considérée comme pendante car les deux sommets de l’arête sont incident uniquement à cette arête. Il en est de même pour une arête isolée qui n’est pas non plus considérée comme pendante.
Comme chaque cellule d’une carte est défini par un ensemble de brins, une cellule c1 est uniquement incidente à c2 si c1 ⊆ c2.
Sur l’exemple de la Fig. 3.2, l’arête a3 est pendante. En effet, le sommet s3 est incident uniquement à a3, et le second sommet s2 est incident à au moins une autre arête que a3 (dit autrement, s3 est de degré un et s2 est de degré supérieur à un).
Intuitivement et de manière générale dans une carte de dimension n, la suppression d’une i-cellule consiste à supprimer cette cellule, et à fusionner éventuellement entre elles les deux (i+1)-cellules lui étant incidentes (cf. exemples Fig. 3.3 et Fig. 3.4). La contraction d’une i-cellule est l’opération duale de la suppression. Elle consiste à contracter cette cellule en une (i−1)-cellule (cf. exemple Fig. 3.5). Dans une carte de dimension n, la suppression est donc définie pour les cellules de dimension 0 à n−1, et la contraction pour les cellules de dimension 1 à n.
Figure 3.3: Exemples de suppression en 2D. (a) Une subdivision 2D initiale. (b) Le résultat après la suppression de l’arête a2. Les deux faces f1 et f2 sont fusionnées en une seule face f. (c) Le résultat après la suppression du sommet s1: les deux arêtes a1 et a3 sont fusionnées en une seule arête a. La suppression n’est applicable qu’aux cellules de degré inférieur ou égal à deux : la suppression de s1 n’était donc pas possible dans la subdivision initiale, car son degré était trois, mais elle est devenue possible après la suppression de a2 qui a entraîné la diminution du degré de s1.
Figure 3.4: Exemples de suppression en 3D. (a) Une subdivision 3D initiale. (b) Le résultat après la suppression de la face grise foncée. (c) Le résultat après la suppression de l’arête a1.
Figure 3.5: Exemples de contraction en 2D. (a) Une subdivision 2D initiale. (b) Le résultat après la contraction de la face f. Les deux arêtes a1 et a2 ont fusionnées en une seule arête a. (c) Le résultat après la contraction de l’arête a: les deux sommets s1 et s2 ont fusionnés en un seul sommet s.
Pour qu’une i-cellule c puisse être supprimée, il faut qu’il y ait au plus deux (i+1)-cellules incidentes à c. En effet, il est autrement impossible de savoir automatiquement comment recoller entre elles les cellules incidentes à c en conservant la propriété de quasi-variété des cartes.
Par exemple, la suppression du sommet s1 de la Fig. 3.2 qui est incident aux trois arêtes a1, a2 et a3, devrait entraîner la création d’une hyper-arête étant l’union des trois, ce qui n’est pas représentable avec une carte.
Ajouter une précondition sur la cellule à supprimer permet de résoudre ces problèmes, sans limiter les possibilités offertes à l’utilisateur. En effet, il est ensuite possible de faire une opération de plus haut niveau enchaînant une suite d’opérations atomiques, chacune respectant les préconditions de l’opération de base (sur l’exemple de la Fig. 3.2, nous pouvons envisager une opération de plus haut-niveau permettant de supprimer s1 en commençant par supprimer une arête lui étant incidente).
Cette contrainte intuitive se traduit en pratique par la définition de cellule supprimable.
Remarquons que la précondition de l’opération ne s’applique pas pour i=n−1 (car n+1 n’existe pas dans une carte de dimension n) : une n−1 cellule peut toujours être supprimée dans une nG-carte. En effet, les cartes représentant des quasi-variétés, une (n−1)-cellule est toujours incidente à au plus deux n-cellules dans une nG-carte, et peut donc toujours être supprimée. Par contre une n-cellule c n’est jamais supprimable car il n’existe pas de (n+1)-cellules incidentes à c à fusionner.
L’opération de i-suppression dans une nG-carte peut maintenant être définie (cf. Def. 50). Pour supprimer une i-cellule c dans une G-carte donnée, il suffit de redéfinir les involutions αi des brins qui sont i-voisins de c (notés BV). Cette redéfinition est locale et nécessite uniquement un parcours des brins de c.
Lors de la redéfinition des αi pour les brins de BV, nous utilisons un chemin de brins défini par ( αi αi+1 )k αi. Ce chemin permet, à partir d’un brin de b′ ∈ BV, de rentrer dans la cellule supprimée (en utilisant αi) puis de traverser cette cellule (en utilisant αi+1 et αi jusqu’à sortir de la cellule supprimée). Il faut éventuellement itérer ces deux dernières involutions (ce qui explique le k) afin de traiter le cas où la cellule est repliée sur elle-même (cas des multi-incidences cf. l’exemple d’une boucle en 2D Fig. 3.9).
Remarquons que pour les brins b′ ∈ B′−BV, b′αi′=b′(αiαi+1)kαi avec k=0 qui est le plus petit entier tel que b′αi′ ∈ BV.
Nous pouvons voir différents exemples de suppression dans les Figs. 3.6 à 3.9 : tout d’abord un exemple de 0-suppression en 1D (Fig. 3.6), puis de 0-suppression en 2D (Fig. 3.7), de 1-suppression en 2D (Fig. 3.8) et enfin un cas de multi-incidence où k=2 (Fig. 3.9).
[a][b]
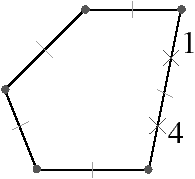
Figure 3.6: 0-suppression en 1D. (a) La 1G-carte initiale. c=⟨α1⟩(2)={2,3} (les brins marqués avec □), cα0={1,4} = BV (les brins marqués avec ×). (b) Le résultat après la 0-suppression. La 0-suppression consiste simplement à définir 1α0′=1(α0α1)α0=4 ∈ BV et 4α0′=4(α0α1)α0=1 ∈ BV.
Figure 3.7: 0-suppression en 2D. (a) La 2G-carte initiale. c=⟨α1,α2⟩(2) (les brins marqués avec □), cα0 = BV (les brins marqués avec ×). (b) Le résultat après la 0-suppression. Par exemple, 1α0′=1(α0α1)α0=4 ∈ BV
[a][b]

Figure 3.8: Cas général de la 1-suppression en 2D. (a) La 2G-carte initiale. Les brins de l’arête à supprimer sont marqués avec ∘. (b) Le résultat après la 1-suppression.
[a][b]
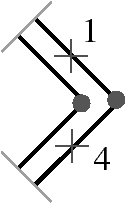
Figure 3.9: 1-suppression en 2D dans un cas de multi-incidence : ici une boucle. (a) La 2G-carte initiale. (b) Le résultat après la 1-suppression. Par exemple, 1α′1=1(α1α2)(α1α2)α1=4 ∈ BV (car 1(α1α2)α1 ∉BV, ce brin appartient à c et à cα1).
Dans le cas général, lorsque la i-cellule c supprimée est incidente à deux (i+1)-cellules distinctes c1 et c2, et qu’aucune (i−1)-cellule incidente à c n’est de degré un, l’opération de suppression entraîne la disparition de la cellule c et la fusion des deux cellules c1 et c2 en une seule cellule. Il n’y a pas d’autre disparition ou fusion de cellules. De ce fait, la caractéristique d’Euler-Poincaré généralisée reste inchangée au cours de l’opération car le nombre de cellules diminue d’un pour deux dimensions consécutives (i et i+1), et ces nombres sont additionnés avec des signes opposés dans la formule d’Euler-Poincaré.
Par contre, lorsque la i-cellule supprimée c est incidente deux fois à la même cellule c1=c2 (c-à-d c est de degré un), plusieurs cas peuvent se produire, entraînant ou non des modifications topologiques. Ces cas dépendent de la présence et de la position de (i−1)-cellules de degré un incidentes à c (ces configurations et l’impact des suppressions sur les modifications topologiques sont détaillés Section 6.2). Mais dans tout ces cas, même s’il y a changement de topologie, l’opération est valide car nous pouvons prouver que son résultat est toujours une nG-carte. Il en est de même si la suppression entraîne une déconnexion en plusieurs composantes connexes, voire même si le résultat est une carte vide (par exemple dans le cas d’une G-carte composée d’une seule arête qui est supprimée). Ce sera ensuite les applications qui selon le cadre d’utilisation auront à charge d’ajouter des contraintes pour satisfaire leurs besoins spécifiques.
L’opération de contraction se définit de manière similaire à l’opération de suppression. En effet, la i-suppression est l’opération duale de la (n−i)-contraction. En utilisant la définition de G-carte duale (Def. 32), nous pouvons transformer la définition de la i-suppression en définition de la (n−i)-contraction simplement en remplacant les indices i par (n−i), i+1 par (n−i−1) et i+2 par (n−i−2). Pour obtenir la définition de la i-contraction et non de la (n−i)-contraction, il faut ensuite renommer (n−i) en i, et donc remplacer (n−i−1) par i−1 et (n−i−2) par i−2. Ces remplacements doivent être faits dans la définition de cellule supprimable qui devient la définition de cellule contractible, ainsi que dans la définition de l’opération de suppression qui devient l’opération de contraction.
Nous pouvons voir deux exemples de contraction dans les Figs. 3.10 et 3.11 : le premier montrant la contraction d’une arête dans une 1G-carte et le second une contraction d’arêtes dans une 2G-carte.
[a][b]
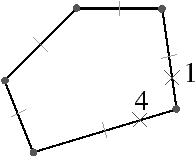
Figure 3.10: 1-contraction en 1D. (a) La 1G-carte initiale. Les brins de l’arête contractée sont marqués avec •, et ceux de BV avec ×. (b) Le résultat après la 1-contraction.
[a][b]
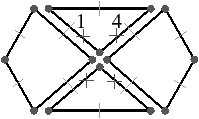
Figure 3.11: 1-contraction en 2D. (a) La 2G-carte initiale. Les brins de l’arête contractée sont marqués avec •, et ceux de BV avec ×. (b) Le résultat après la 1-contraction.
Comme pour la suppression, la contraction d’une i-cellule c peut entraîner des modifications topologiques ou non selon les configurations, et peut entraîner des suppressions d’autres cellules incidentes à c, la différence étant que par dualité, il faudra s’intéresser aux (i+1)-cellules incidentes à c (et non plus aux (i−1)-cellules comme pour la suppression)
Les deux définitions précédentes permettent d’effectuer la suppression ou la contraction d’une seule cellule. Il est intéressant de pouvoir effectuer plusieurs opérations simultanément, pour des raisons de flexibilité et d’efficacité. Pour cela, il faut marquer les cellules à supprimer et à contracter, avec la dimension et le type de l’opération. Les opérations peuvent être appliquées simultanément si les cellules sont disjointes et si chaque cellule vérifie la précondition éventuelle des opérations unitaires. La G-carte résultante peut alors être calculée directement, les α′ se définissant en une seule fois à l’aide de chemins de brins supprimés et contractés dans la carte initiale.
| i+1 si bj = b(αiαl1) … (αiαlj−1)αi ∈ Si, |
| i−1 sinon (bj ∈ Ci) . |
Chaque brin est marqué avec la dimension et le type de l’opération appliquée sur la cellule incidente. Tester si les cellules sont disjointes revient simplement à vérifier que chaque brin est marqué avec au plus une seule opération.
De manière intuitive, pour chaque brin b ∈ BVi, nous «parcourons» les brins de la G-carte en partant de bαi et appliquant soit (αi+1αi) si le brin courant appartient à une cellule supprimée, soit (αi−1αi) si le brin appartient à une cellule contractée. Nous arrêtons le parcours dès que le brin courant n’appartient ni à une cellule supprimée ni à une cellule contractée. Nous avons alors trouvé la nouvelle image par αi du brin de départ (nous retrouvons ici la notion de chemin de connexion introduite en 2D dans [BK02] et détaillée au chapitre 5).
Ce principe utilise le fait que les cellules sont disjointes : chaque brin rencontré durant le parcours est marqué avec au plus une seule opération, il n’y a donc aucune ambiguïté sur le type d’opération. Cette précondition implique que, à partir de b ∈ BVi, nous allons parcourir uniquement des i-cellules supprimées et/ou des i-cellules contractées. En effet, c’est le cas pour la première cellule rencontrée incidente à b αi (par définition de BVi) et c’est le cas de proche en proche pour les cellules parcourues. Plus précisément, soit b′ appartenant à une i-cellule supprimée (resp. contractée) : b″=b′αi+1 (resp. b″=b′αi−1) appartient à la même i-cellule (par définition des i-cellules). Supposons b‴=b″αi ∉ BVi et la dimension de l’opération associée à b‴ soit j ≠ i. Comme b″ et b‴ appartiennent à la même j-cellule (car ils sont reliés par αi), b″ est marqué avec deux opérations différentes ce qui contredit la précondition sur les cellules disjointes.
Pour la même raison, nous pouvons observer que les chemins reliant deux brins quelconques pour deux dimensions différentes sont disjoints, sauf éventuellement à leurs extrémités. En effet, un brin peut appartenir à plusieurs BVi différents lorsqu’il est voisin de plusieurs cellules de dimension différentes contractées ou supprimées. Par contre, les chemins sont disjoints grâce à la précondition sur les cellules disjointes.
Cette remarque nous permet de garantir que la carte résultante est indépendante de l’ordre dans lequel nous redéfinissons les α′i. En effet, en pratique, il est plus simple de modifier directement la G-carte en mettant à jour ses involutions, sans avoir à la dupliquer pour définir les nouvelles involutions α′i en fonction des anciennes αi. Cette possibilité est réalisable grâce à l’indépendance des chemins par rapport à l’ordre des redéfinitions. Cette indépendance permet également d’envisager l’application en parallèle des redéfinitions.
Enfin, nous pouvons montrer que la G-carte résultante de l’application simultanée d’un ensemble de suppressions et contractions est la même celle obtenue en appliquant chaque opération unitaire de manière successive, et ce dans n’importe quel ordre. Le principe de la démonstration repose à nouveau sur la propriété des cellules disjointes, mais utilise également le fait que pour deux i-cellules adjacentes, le chemin traversant les deux cellules est la concaténation des deux chemins unitaires traversant chaque cellule. De ce fait, la redéfinition simultanée d’un α′i peut-être ramenée à une suite de redéfinitions successives de α′i, un pour chaque opération unitaire.
Un exemple illustrant l’opération de suppression et contraction simultanées d’un ensemble de cellules est présenté Fig. 3.12. Sur cet exemple, les quatre opérations existantes en dimension deux sont simultanément utilisées : la 1- et 2-contraction, et la 0- et 1-suppression.
[a][b]
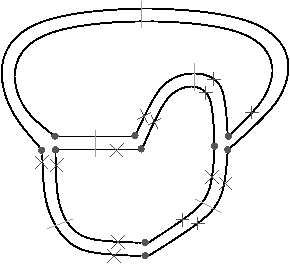
Figure 3.12: Un exemple 2D de suppression et contraction simultanées de cellules de différentes dimensions. (a) La 2G-carte initiale. Les brins appartenant à une 1-cellule supprimée (resp. 0-cellule supprimée, 1-cellule contractée, 2-cellule contractée) sont marqués avec ∘ (resp. □, •, filled square). Les brins marqués avec × appartiennent à ∪ BVi. Trois chemins de connexion sont représentés : C1 qui traverse une arête contractée, C2 qui traverse deux sommets contractés, et C3 qui traverse une arête contractée puis une arête supprimée. (b) La 2G-carte obtenue après application de l’opération.
Les deux autres opérations de base, qui sont l’insertion et l’éclatement, sont les opérations inverses des opérations précédentes. Ces opérations permettent de raffiner une subdivision en y ajoutant des cellules.
Des exemples d’insertion sont présentés en 2D Fig. 3.13 et en 3D Fig. 3.14 et des exemples d’éclatement en 2D Fig. 3.15. Une comparaison entre ces exemples et les exemples similaires de suppression et de contraction permet de voir que les paramètres d’entrées de ces nouvelles opérations sont plus complexes. En effet, pour les deux opérations précédentes, la donnée seule de la cellule suffit, les modifications sont ensuite guidées par la configuration des cellules voisines données dans la carte. Pour l’insertion et l’éclatement, la donnée de la cellule ne suffit plus car il y a plusieurs manières d’ajouter cette cellule dans la subdivision existante : il faut également fournir comme paramètre de l’opération la manière de relier la nouvelle cellule à la carte existante.
Figure 3.13: Exemples d’insertion en 2D. (a) Une subdivision 2D initiale. (b) Le résultat après l’insertion du sommet s1 sur l’arête a : l’arête a été découpée en deux arêtes a1 et a3. (c) Le résultat après l’insertion de l’arête a2 entre les sommets s1 et s2. La face f a été découpée en deux faces f1 et f2.
Figure 3.14: Exemples d’insertion en 3D. (a) Une subdivision 3D initiale. (b) Le résultat après l’insertion d’une arête entre les sommets s1 et s2. (c) Le résultat après l’insertion d’une face le long des arêtes a1, a2 et a3.
Figure 3.15: Exemples d’éclatement en 2D. (a) Une subdivision 2D initiale. (b) Le résultat après l’éclatement de s en arête. Le sommet s a été éclaté dans les deux sommets s1 et s2. (c) Le résultat après l’éclatement de a en face. L’arête a a été éclatée dans les deux arêtes a1 et a2.
La définition de l’insertion d’une i-cellule dans une nG-carte s’inspire directement de la i-suppression qui est l’opération inverse. La différence principale se situe dans les données de l’opération. Nous avons maintenant G une nG-carte, c la cellule à insérer, donnée dans une deuxième nG-carte, et une involution γ explicitant comment relier les brins de G et les brins de c.
Les contraintes de la Def. 54 obligent que la cellule c soit supprimable, ceci afin que le résultat de l’insertion soit une quasi-variété mais aussi pour que l’insertion soit bien l’opération inverse de la suppression.
Remarquons que dans la définition de G′, seul αi est redéfini pour les brins de BV ∪ BV′. En effet, l’insertion entraîne la couture des brins de BV avec les brins de BV′ par αi (qui est donnée par γ). Toutes les autres involutions restent inchangées. Enfin, nous avons prouvé dans [BDSM08] que cette opération est valide, c’est-à-dire que G′ est bien une nG-carte.
La Fig. 3.16 montre un exemple d’insertion pour une cellule vérifiant les trois préconditions de l’opération (cas Fig. 3.16(c)), ainsi qu’un exemple où la troisième précondition n’est pas vérifiée (cas Fig. 3.16(a)). Pour ce dernier exemple, 3α0=4 est différent de 3γ α1 γ=3. L’insertion d’une telle cellule donne un résultat qui n’est plus une G-carte car nous modifions α0 pour le brin 3, mais pas pour le brin 4.
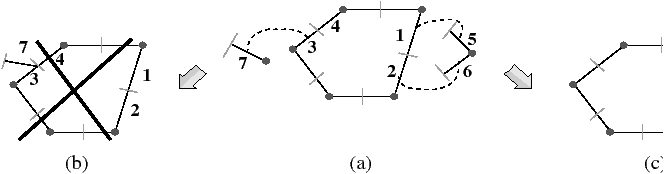
Figure 3.16: 0-insertion en 1D. (a) 1G-carte initiale G qui correspond à l’orbite ⟨α0, α1⟩ (1 ). Une 0-cellule c1 = ⟨α1⟩ ( 7) = {7}, BV1 = {3}, BV′1 = {7}. Une seconde 0-cellule c2 = ⟨α1⟩ ( 5) = {5, 6 }, BV2 = {1,2 }, BV′2 = {5,6 }. L’involution γ est représentée par les traits pointillés : γ relie respectivement les brins 1,2 et 3 avec les brins 5,6 et 7. (b) Résultat invalide après insertion de c1 dans G (α0 n’est plus une involution car 3 α0 = 7 et 4 α0 = 3). Ce cas est interdit par les préconditions de l’opération d’insertion. (c) Résultat valide après insertion de c2 dans G (la précondition b α0 = b γ α1 γ est satisfaite pour tout les brins de c2).
L’exemple de la Fig. 3.17 montre un autre cas où la troisième condition de la Def. 54 n’est pas vérifiée. En effet, 1α0=1 est différent de 1γ α1 γ=2. Dans ce cas, l’insertion de la cellule donne une G-carte valide, mais l’opération n’est alors pas l’inverse de la suppression.
[a][b]
[c]
Figure 3.17: Exemple où la troisième précondition de la 0-insertion n’est pas satisfaite. (a) Une 1G-carte G et un sommet à insérer c={3,4}. L’involution γ est représentée par les traits pointillés. BV = {1,2} et BV′ = {3,4} sont deux sous-ensembles de brins, chaque brin de ces ensembles étant 0-libre. (b) La 1G-carte G′ obtenue après insertion de c dans G. (c) La 1G-carte obtenue après suppression de c dans G′: les brins 1 et 2 sont maintenant 0-cousus alors qu’ils étaient 0-libres avant l’insertion : la suppression n’est pas l’inverse de l’insertion.
La Fig. 3.18 présente deux exemples de 0-insertion dans une 2G-carte. Dans les deux cas, les trois préconditions de l’opération sont vérifiées. Cet exemple montre que la donnée explicite de l’involution γ est nécessaire car il y a plusieurs manières d’insérer la même cellule dans la même G-carte, le long des mêmes brins. Sur cet exemple, la seule différence entre les deux cas porte sur la manière dont les brins de BV et BV′ sont mis en relation.
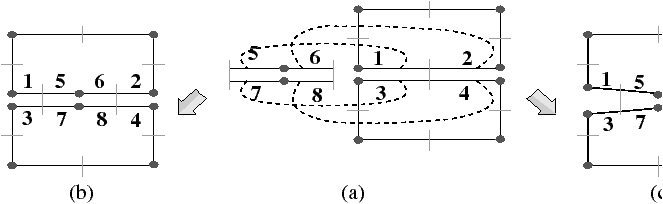
Figure 3.18: 0-insertion en 2D. (a) 0-cellule C=⟨α1,α2⟩ ( 5 ) = {5,6,7,8}, BV = {1,2,3,4}, BV′ = C. La 2G-carte initiale G égale à l’orbite ⟨α0, α1, α2⟩ ( 1). L’involution γ1 est représentée par les traits pointillés (respectivement entre les brins 1,2,3,4 et les brins 5,6,7,8) L’involution γ2 (non représentée sur la figure) relie respectivement les brins 1,2,3,4 avec les brins 5,8,7,6. (b) La 2G-carte obtenue après insertion de c dans G en utilisant l’involution γ1. (c) La 2G-carte obtenue après insertion de c dans G en utilisant l’involution γ2.
La Fig. 3.19 présente un exemple de 1-insertion dans une 2G-carte. Les trois préconditions de l’opération sont vérifiées, le résultat est une 2G-carte valide.
[a][b]
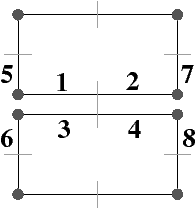
Figure 3.19: 1-insertion en 2D dans le cas général. (a) Les brins de l’arête à insérer sont numérotés de 1 à 4. L’involution γ est représentée par les traits pointillés. (b) Le résultat de l’insertion.
La Fig. 3.20 présente un second exemple de 1-insertion dans une 2G-carte mais cette fois pour un cas particulier : l’insertion d’une boucle. La seule différence avec l’exemple précédent est que ici, k=1 alors que dans les cas précédents, k était égal à 0. En effet, durant le parcours du chemin de redéfinition de α1′, il faut traverser l’arête avant de retomber sur un brin de BV′. Comme les trois préconditions de l’opération sont vérifiées, le résultat est une 2G-carte valide.
[a][b]
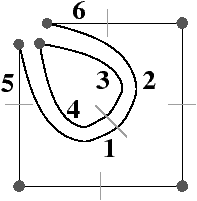
Figure 3.20: 1-insertion en 2D dans un cas particulier : ici l’insertion d’une boucle. (a) Les brins de l’arête à insérer sont numérotés de 1 à 4. L’involution γ est représentée par les traits pointillés. (b) Le résultat de l’insertion. La troisième précondition de l’opération est vérifiée car 5 α1 = 5 γ α2 ( α1 α2 ) γ =6.
De manière analogue à la contraction pour la suppression, l’opération d’éclatement se définit de manière similaire à l’opération d’insertion. En effet, le i-éclatement étant l’opération duale de la (n−i)-insertion, il suffit de remplacer les indices i+1 par (i−1) et i+2 par (i−2).
Les Figs. 3.21 et 3.22 montrent deux exemples d’éclatement, le premier en 1D et le second en 2D. Le principe est le même que pour l’insertion, la différence étant uniquement sur les préconditions de l’opération qui garantissent que l’éclatement est l’opération inverse de la contraction.
[a][b]
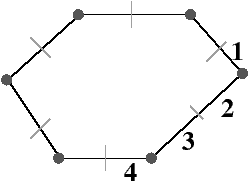
Figure 3.21: 1-éclatement en 2D. (a) Les brins de l’arête à insérer sont numérotés 2 et 3. L’involution γ est représentée par les traits pointillés. (b) Le résultat de l’éclatement.
[a][b]
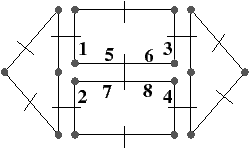
Figure 3.22: 1-éclatement en 2D. (a) La 2G-carte initiale et l’arête à insérer (brins numérotés de 5 à 8). L’involution γ est représentée par les traits pointillés. (b) Le résultat de l’éclatement.
Les deux définitions précédentes permettent d’effectuer l’insertion ou l’éclatement d’une seule cellule. Comme pour les opérations de suppression et contraction, il est intéressant de pouvoir effectuer plusieurs opérations simultanément. La donnée de l’opération généralisée est maintenant une nG-carte G et une seconde nG-carte G′ contenant l’ensemble des cellules à insérer et à éclater. Chaque brin de G′ est marqué avec la dimension et le type de l’opération (insertion ou éclatement). Les opérations peuvent être appliquées simultanément si les cellules sont disjointes et si chaque cellule vérifie la précondition éventuelle des opérations unitaires. La G-carte résultante peut alors être calculée directement, les nouvelles involutions se définissant en une seule fois à l’aide des involutions γ.
| i+1 si bj = b γi αl1 (αiαl2) … (αiαlj−1) ∈ I, |
| i−1 sinon (c-à-d bj ∈ E) . |
Comme pour l’opération de suppression et contraction simultanées, les cellules doivent être disjointes, et vérifier la contrainte d’être supprimables pour les cellules à insérer et contractibles pour les cellules à éclater. De plus, toutes les cellules de G′ doivent être marquées à insérer ou à supprimer. En effet, sans cette contrainte, l’opération ne serait pas l’opération inverse de la suppression et contraction simultanées car les brins n’appartenant à aucune cellule à insérer ou éclater ne seraient pas supprimés par l’opération de suppression et contraction. De ce fait, la carte obtenue après insertion et éclatement simultanés, puis suppression et contraction simultanées, ne serait pas isomorphe à la carte initiale.
Pour cette opération généralisée, il y a maintenant n+1 involutions γi, une par dimension de la subdivision. Chaque involution doit vérifier les préconditions de l’opération de base :
De plus, le fait que les γi soient des involutions entraîne qu’un brin b ne peut être utilisé que pour insérer ou éclater une unique i-cellule. Par contre, un même brin peut être utilisé pour plusieurs cellules de dimensions différentes.
La Fig. 3.23 montre un exemple de l’opération d’insertion et d’éclatement simultanés. Sur cet exemple, les quatre opérations existantes en dimension deux sont simultanément utilisées : les 1- et 2-éclatements, et les 0- et 1-insertions.
[a][b]
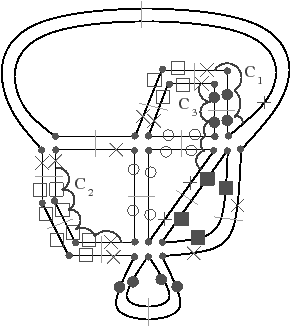
Figure 3.23: Un exemple en 2D d’insertion et éclatement simultanés de cellules de différentes dimensions. (a) La 2G-carte initiale et les cellules à insérer et éclater. Les brins appartenant à une 1-cellule insérée (resp. 0-cellule insérée, 1-cellule éclatée, 2-cellule éclatée) sont marqués avec ∘ (resp. □, •, filled square). Les brins marqués avec × appartiennent à ∪ BVi. Les involutions γi sont représentées par les traits pointillés, avec un numéro indiquant la dimension de l’opération. (b) La 2G-carte obtenue après application de l’opération.
Les opérateurs d’Euler sont les opérateurs de base permettant de modifier une variété 2D. L’intérêt de ces opérateurs est de pouvoir servir de brique de base pour modifier un objet, tout en contrôlant l’évolution de ses caractéristiques topologiques. Ces opérateurs ont été beaucoup étudiés [Bau74, EW79, BHS80, Män88, Str06] et il a été prouvé dans [Män84] que ces opérateurs forment un «ensemble complet», c’est-à-dire que n’importe quel polyèdre peut être construit par une séquence finie de ces opérateurs. Ces opérateurs sont classifiés en comptant :
La formule d’Euler-Poincaré peut s’étendre pour tenir compte des coques, des cycles internes et du nombre de bord : v − (e+l) + (f + b) = 2(s−g), avec g le genre de l’objet (cf. exemple Fig. 3.24). Intuitivement, une face est ajoutée pour chaque bord (afin de fermer les surfaces) ce qui explique le (f + b), et une arête est ajoutée pour chaque cycle interne (pour relier ce cycle au cycle externe pour se ramener au cas d’une face représenté par un seul cycle). Pour un complexe fermé b=0, ayant une seule coque s=1, et tel que chaque face soit décrite par un seul cycle l=0, nous retrouvons la formule classique donnée Section 2.1.4 : v − e + f = 2−2g.
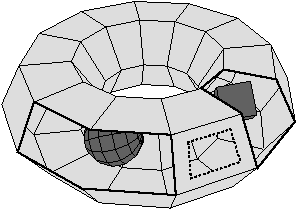
Figure 3.24: Exemple de complexe cellulaire illustrant la notion de coques, de cycles internes, et de bords. Cet objet est composé de trois coques c=3 (une pour le tore extérieur avec les faces en gris clair, une pour la sphère et une pour le cube intérieur avec les faces en gris foncé). Il y a un cycle interne l=1 (dessiné en pointillé), et trois bords b=3 (dessinés en gras, un bord correspond au cycle interne). Cet objet est composé de 158 sommets, 314 arêtes et 158 faces2. Nous obtenons donc 2(3−g)=158 − (314+1) + (158 + 3)=4 et donc g=1 : c’est bien le genre d’un tore.
Il existe 99 opérateurs d’Euler «atomiques» qui ne modifient qu’une seule des caractéristiques du complexe cellulaire (cf. [Str06] pour la liste exhaustive). Le nombre de ces opérateurs peut être réduit à 39 en considérant des combinaisons des opérateurs atomiques autorisant la modification de deux ou trois caractéristiques. Enfin, il est possible de sélectionner seulement 10 opérateurs et de prouver que n’importe quel polyèdre valide peut-être obtenu à partir de n’importe quel autre polyèdre valide en utilisant une séquence finie de ces opérateurs. Ces 10 opérateurs sont donnés Fig. 3.25. Il y a 5 opérateurs de type makeX qui ajoutent des éléments, et qui correspondent à nos insertions ou éclatements, et les 5 opérateurs inverses de type killY, qui correspondent à nos suppressions ou contractions.
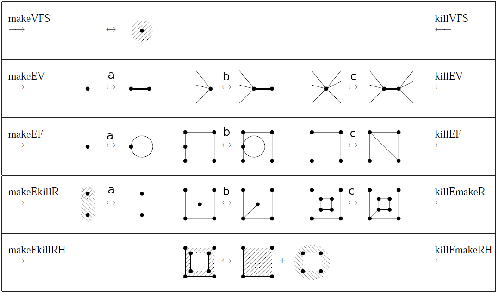
Figure 3.25: Les 10 opérateurs d’Euler permettant de créer n’importe quel complexe cellulaire. Image tirée de [Hav05].
Chaque opérateur peut s’écrire de la forme MaKb avec M pour make (construit) l’entité (ou les entités) a, et K pour kill (détruit) l’entité (ou les entités) b, et chaque entité pouvant être sommet V, arête E, face F, coquille S, bord H ou cycle interne R.
Op. Signification Op. inv. Signification MVFS make a vertex, a face and a shell KVFS kill a vertex, a face and a shell MEV make an edge and a vertex KEV kill an edge and a vertex MEF make an edge and a face KEF kill an edge and a face MEKR make an edge, kill a ring KEMR kill an edge, make a ring MFKRH make a face, kill a ring and a hole KFMRH kill a face, make a ring and a hole
Tableau 3.1: Tableau donnant la liste des 10 opérateurs d’Euler utilisés ici, et leur signification. Il y a 5 opérateurs de construction (makeX) et 5 opérateurs inverses de destruction (killY). Pour les 3 opérateurs au milieu de la Fig. 3.25, il y a 3 sous cas différents, numérotés a, b et c.
Il est facile de vérifier que chaque opérateur correspond à une de nos opérations. Tout d’abord, ces opérateurs étant défini dans le cadre des polyèdres, nous utilisons une 2G-carte. Nous allons maintenant donner pour chaque opérateur d’Euler son équivalent en terme d’opération sur cette 2G-carte.
Il arrive que dans certains cas, un même opérateur corresponde à deux opérations. En effet, dans des cas particuliers (par exemple pour une arête pendante), les cartes obtenues par l’application de deux opérations différentes sont isomorphes (la suppression ou la contraction d’une arête pendante), mais ce n’est pas vrai dans le cas général.
Pour les 5 opérateurs inverses (killY), comme nous avons vu que les suppressions et contractions sont les opérations inverses des insertions et éclatements, nous déduisons directement les opérations associées (par exemple pour l’opérateur KEF qui est l’inverse de MEF, dans les 3 cas (a), (b) et (c), 1-suppression de l’arête. Dans les cas (a) et (b), cela peut également être la 1-contraction de l’arête en sommet).
L’opération de décalage d’arête, illustrée Fig. 3.26, consiste à «pousser» le coté d’une arête le long de l’arête suivante de la même face (et du même volume si nous sommes en 3D). Cette opération est définie ici pour des configurations respectant certaines propriétés, et uniquement en 2D et en 3D.
[a][b]
[c]
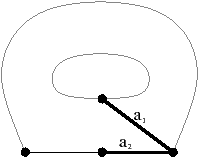
Figure 3.26: Un exemple 2D de décalage d’arête. L’arête a1 est décalée le long de l’arête a2. Il est possible de voir ce décalage comme une déformation continue passant de la configuration initiale (a) à la configuration finale (c).
Commençons tout d’abord par le cas 2D. Les contraintes à vérifier sont :
Ces contraintes assurent que la modification est locale à la face incidente à cette arête, qu’il existe bien une autre arête le long de laquelle décaler l’arête, et que l’arête le long de laquelle nous allons décaler c1(b) n’est pas une boucle.
Nous notons ac=⟨h(α0,α1)⟩(b), ce sont les brins de l’arête du coté du sommet incident à b, BV= ac α1 − ac, les brins 1-cousus à ac n’appartenant pas à ac, b2=bα2, d1=bα10 et d2=d1α1, et D={d1,d2}.
La 2G-carte obtenue en décalant l’arête a le long de l’arête suivant a du coté du sommet incident à b est G′=(B,α0′,α1′,α2′) définie par :
Cette opération de décalage d’arête peut être vue comme la suppression de l’arête, mais uniquement d’un coté de l’arête, puis comme l’insertion de cette arête sur le sommet suivant. Pour cette raison, nous retrouvons dans la Def. 57 les trois premiers points qui proviennent directement de la définition de la suppression d’arête, mais en se limitant à un seul côté de l’arête (ce qui se traduit en pratique par l’utilisation de l’orbite ⟨h(α0,α1)⟩(b) au lieu de l’orbite arête ⟨h(α1)⟩(b)), et les deux derniers points qui proviennent de la définition de l’insertion d’arête.
La Fig. 3.27 présente un exemple de décalage d’arête 2D dans le cas général. Nous souhaitons décaler l’arête incidente au brin b dans la G-carte initiale de la Fig. 3.5 sur l’arête suivante du côté du sommet incident au brin b. Ce décalage est réalisé en modifiant les relations α1′ pour les brins o1, o2, et les brins d1, d2. Le troisième point de la Def. 57 va fixer α1′(o1)=o2 et α1′(o2)=o1, et les deux derniers points de cette même définition vont fixer α1′(d1)=b2, α1′(b2)=d1, et α1′(d2)=b, α1′(b)=d2. Nous pouvons vérifier sur l’exemple que ces 6 modifications correspondent bien au décalage de l’arête.
[a][b]
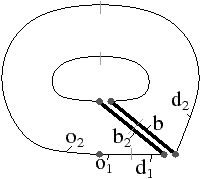
Figure 3.27: Le cas général de décalage d’arête en 2D. (a) La configuration initiale. L’arête c1(b) est à décaler. Les brins d1 et d2 donnent la position où l’arête va être décalée. Les brins o1 et o2 sont les voisins de l’arête qui vont être modifiés : BV={o1,o2}. (b) La G-carte obtenue après le décalage.
Nous pouvons vérifier sur les exemples des Figs. 3.28 et 3.29 que le décalage d’arête fonctionne correctement dans les cas particuliers où le brin b2 est 1-libre, et le cas où le brin bα10 est 1-libre. Les autres possibilités de brin libre sont interdites par les conditions de la Def. 57.
[a][b]
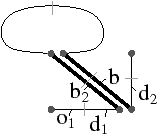
Figure 3.28: Un cas particulier de décalage d’arête en 2D lorsque le brin b2 est 1-libre. (a) La configuration initiale, avec l’arête c1(b) à décaler. (b) La G-carte obtenue après le décalage. Ce cas est traité correctement par le point 3 de la Def. 57 en fixant α1′(o1)=o1 avec k=2.
[a][b]
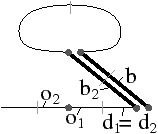
Figure 3.29: Un autre cas particulier de décalage d’arête en 2D lorsque le brin bα10 est 1-libre, ce qui entraîne d2=d1. (a) La configuration initiale, avec l’arête c1(b) à décaler. (b) La G-carte obtenue après le décalage. Ce cas est traité correctement par le point 5 de la Def. 57 en fixant α1′(b)=b.
La définition de décalage d’arête 2D s’étend directement en dimension 3. En effet, par définition des G-cartes, il existe deux cas possibles : soit l’arête à décaler est 3-libre, et alors tous les brins de la face sont 3-libres, soit l’arête à décaler n’est pas 3-libre et alors il existe deux demi-faces isomorphes ayant tout leurs brins reliés par α3 deux à deux. Dans le premier cas, la définition du décalage d’arête se ramène au cas 2D, et dans le second cas il faut effectuer deux redéfinitions : une pour chaque brin de la demi-face, et une seconde pour leurs images par α3. La Def. 58 présente cette opération de décalage d’arête en 3D.
Nous notons ac=⟨h(α0,α1)⟩(b), ce sont les brins de l’arête du coté du sommet incident à b, BV= ac α1 − ac, les brins 1-cousus à ac n’appartenant pas à ac, b2=bα2, b3=bα3 et b4=b2α3 ; d1=bα10, d2=d1α1, d3=d1α3 et d4=d2α3, et D={d1,d2,d3,d4}. La 3G-carte obtenue en décalant l’arête a le long de l’arête suivant a du coté du sommet incident à b est G′=(B,α0′,α1′,α2′,α3′) définie par :
Cette définition consiste simplement à considérer deux brins supplémentaires par rapport au cas 2D, qui sont les brins d3=d1α3 et d4=d2α3. La première partie de la définition (les points 1, 2 et 3) sont inchangés car la définition est générique. Pour les points 4 et 5, nous ajoutons la définition de α1′ pour ces deux brins supplémentaires, en s’assurant au préalable que nous ne sommes pas dans le cas d’un brin 3-libre (d3=d1 et d4=d2) puisqu’il n’y a alors rien à faire pour ces brins dans ce cas.
Nous montrons Fig. 3.30 un exemple de décalage d’arête 3D dans le cas général, lorsque la face concernée n’est pas 3-libre (autrement nous nous ramenons au cas 2D). Nous voyons bien sur cet exemple que, comme les deux demi-faces concernées par le décalage sont isomorphes, le décalage de l’arête 3D est équivalent à appliquer deux fois l’opération de décalage 2D, une fois par demi-face. De ce fait, les différents cas particulier présentés en 2D vont fonctionner de manière identique en 3D, et nous ne les détaillons pas à nouveau.
[a][b]
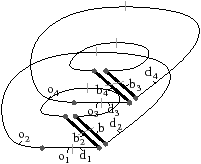
Figure 3.30: Le cas général de décalage d’arête en 3D. (a) La configuration initiale. L’arête c1(b) est à décaler. Les brins d1, d2, d3 et d4 donnent la position où l’arête va être décalée. Les brins o1, o2, o3 et o4 sont les voisins de l’arête qui vont être modifiés : BV={o1,o2,o3,o4}. (b) La G-carte obtenue après le décalage.
Dans ce chapitre, nous avons défini les quatre opérations de base permettant soit de simplifier une subdivision (pour la suppression et la contraction), soit à l’inverse de la raffiner (pour l’insertion et l’éclatement). Ces opérations sont définies de manière générique en dimension quelconque. Les seules contraintes sont celles nécessaires pour garantir que le résultat de l’opération soit bien une G-carte. Nous avons montré que ces opérations permettent de représenter les opérateurs d’Euler en 2D. Comme il a été prouvé que ces opérateurs sont complets (c’est-à-dire que n’importe quel polyèdre 2D peut être construit par une séquence finie de ces opérateurs), cela montre également que nos opérations sont complètes pour les 2G-cartes. Il serait intéressant d’étendre cette preuve aux dimensions supérieures, en montrant toute nG-carte peut être obtenue à partir de n’importe quelle nG-carte par une suite finie d’opérations de base.
Les quatre opérations définies dans ce chapitre peuvent être utilisées comme briques de base dans de nombreuses autres opérations et dans différents cadres. Il sera alors parfois nécessaire de rajouter des contraintes spécifiques, mais les opérations pourront s’appliquer sans aucune modification. Enfin, nous avons défini ces opérations sur les cartes généralisées afin de profiter de leur homogénéité, mais ces définitions se transcrivent pour les cartes combinatoires en utilisant les algorithmes de conversion présentés au chapitre 2.
Nous avons également défini l’opération de décalage d’arête permettant de modifier un sommet dans l’objectif de le rendre supprimable, tout en préservant les autres cellules et relations d’incidence. Contrairement aux quatre opérations précédentes, cette opération est définie dans un cas particulier (uniquement pour les arêtes) et seulement en 2D et 3D. Nous avons commencé à étudier l’extension de cette opération à d’autres types de cellules (par exemple pour décaler les faces) et en toute dimension, mais ce travail n’a pas encore totalement abouti. De plus, nous souhaitons également étudier l’opération duale qui permettrait de rendre possible la contraction d’une cellule en diminuant son co-degré.
Pour toutes ces opérations, il est assez simple de déduire l’algorithme correspondant à la définition. Nous ne l’avons pas fait dans ce chapitre afin de ne pas l’alourdir, mais certains de algorithmes ont été détaillés dans les références suivantes [Dam01, DBF04, Dam08], dans le cadre des cartes combinatoires. De plus, tout ces algorithmes sont locaux car les seules modifications concernent les brins voisins des cellules concernées. De ce fait, la complexité de ces algorithmes est à chaque fois linéaire en nombre de brins des cellules.
Nous verrons dans la suite de ce manuscrit que ces opérations sont au cœur de nos travaux et sont abondamment utilisés dans différents cadres comme par exemple le calcul d’une carte minimale représentant une image étiquetée, la segmentation d’images, ou le calcul de groupes d’homologie.
Nous souhaitons maintenant pouvoir étendre les deux généralisations présentées dans ce chapitre afin de fournir des opérations permettant encore plus d’opérations différentes de manière simultanée. Il est par exemple souhaitable de pouvoir supprimer en une seule fois une arête et le sommet incident à cette arête qui était de degré trois, mais devient de degré deux après la suppression de l’arête. Ce type d’opération est intéressant au niveau de la complexité de l’opération car elle évite plusieurs itérations, mais elle est surtout intéressante dans le cadre des pyramides de cartes, que nous allons présenter au chapitre 5, pour éviter la création de nombreux niveaux intermédiaires inutiles.
Nous allons maintenant nous intéresser à l’utilisation des cartes pour représenter des images 2D/3D. Nous allons voir que la définition du modèle, mais également les opérations que nous allons mettre en place s’appuient sur les opérations de base que nous venons de définir.


