Page d'accueil
Page d'accueil Recherches
Recherches Publications
Publications Enseignements
Enseignements Encadrement de Thèses
Encadrement de Thèses CV
CV Coordonnées
CoordonnéesBorder Operator for Generalized Maps
Proc. of 15th International Conference on Discrete Geometry for Computer Imagery (DGCI)
Lecture Notes in Computer Science 5810, pages 300-312, September 2009, Montréal, Canada
Lecture Notes in Computer Science 5810, pages 300-312, September 2009, Montréal, Canada
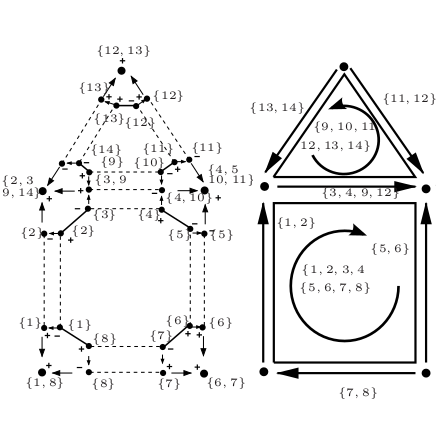
Abstract: In this paper, we define a border operator for the generalized maps, a data structure for representing cellular quasi-manifolds. The interest of this work lies in the optimization of homology computation, by using a model with less cells than models in which cells are regular ones as tetrahedra and cubes. For instance, generalized maps have been used for representing segmented images. We first define a face operator to retrieve the faces of any cell, then deduce the border operator and prove that it satisfies the required property : border of border is void. At last, we study the links between the cellular homology defined from our border operator and the classical simplicial homology.
Keywords: Border operation; Generalized maps; Cellular homology.
Keywords: Border operation; Generalized maps; Cellular homology.
BibTex references
@InProceedings{APDL09,
author = {Alayrangues, S. and Peltier, S. and Damiand, G. and Lienhardt, P.},
title = {Border Operator for Generalized Maps},
booktitle = {Proc. of 15th International Conference on Discrete Geometry for Computer Imagery (DGCI)},
series = {Lecture Notes in Computer Science},
publisher = {Springer Berlin/Heidelberg},
volume = {5810},
pages = {300-312},
month = {September},
year = {2009},
address = {Montr\éal, Canada},
keywords = {Border operation; Generalized maps; Cellular homology.},
url = {https://doi.org/10.1007/978-3-642-04397-0_26}
}
author = {Alayrangues, S. and Peltier, S. and Damiand, G. and Lienhardt, P.},
title = {Border Operator for Generalized Maps},
booktitle = {Proc. of 15th International Conference on Discrete Geometry for Computer Imagery (DGCI)},
series = {Lecture Notes in Computer Science},
publisher = {Springer Berlin/Heidelberg},
volume = {5810},
pages = {300-312},
month = {September},
year = {2009},
address = {Montr\éal, Canada},
keywords = {Border operation; Generalized maps; Cellular homology.},
url = {https://doi.org/10.1007/978-3-642-04397-0_26}
}
Image
 [Retour]
[Retour]