Fully Deformable 3D Digital Partition Model with Topological Control

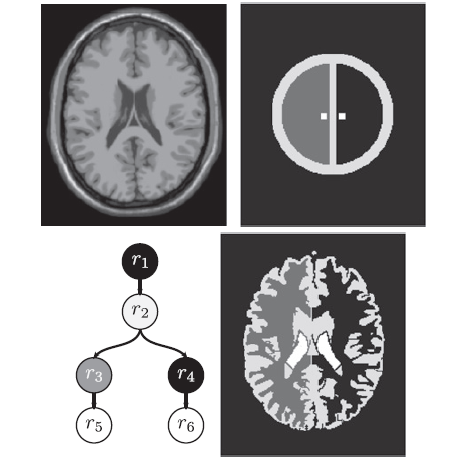
Abstract: We propose a purely discrete deformable partition model for segmenting 3D images. Its main ability is to maintain the topology of the partition during the minimization process. To do so, our main contribution is a new definition of multi-label simple points (ML simple point) that is easily computable. An ML simple point can be relabeled without modifying the overall topology of the partition. The definition is based on intervoxel properties, and uses the notion of collapse on cubical complexes. This work is an extension of a former restricted definition [DupasAl09] that prohibits the move of intersections of boundary surfaces. A deformation process is carried out with a greedy energy minimization algorithm. A discrete area estimator is used to approach at best standard regularizers classically used in continuous energy minimizing methods. We illustrate the potential of our approach with the segmentation of 3D medical images with known expected topology.

Keywords: 3D Image Segmentation; Simple Point; Deformable Model; Intervoxel Boundaries; Multi-Label Image; Cubical complexes.