Polynomial Algorithms for Subisomorphism of nD Open Combinatorial Maps

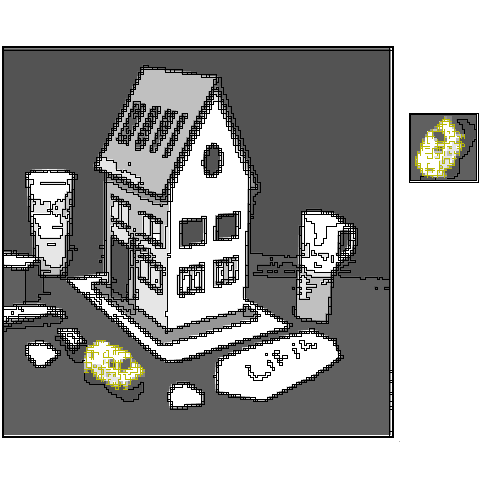
Abstract: Combinatorial maps describe the subdivision of objects in cells, and incidence and adjacency relations between cells, and they are widely used to model 2D and 3D images. However, there is no algorithm for comparing combinatorial maps, which is an important issue for image processing and analysis. In this paper, we address two basic comparison problems, i.e., map isomorphism, which involves deciding if two maps are equivalent, and submap isomorphism, which involves deciding if a copy of a pattern map may be found in a target map. We formally define these two problems for nD open combinatorial maps, we give polynomial time algorithms for solving them, and we illustrate their interest and feasibility for searching patterns in 2D and 3D images, as any child would aim to do when he searches Wally in Martin Handford's books.

Keywords: Open combinatorial maps; Isomorphism and subisomorphism; Pattern detection; 2D and 3D images.