Hierarchical Representation for Rasterized Planar Face Complexes

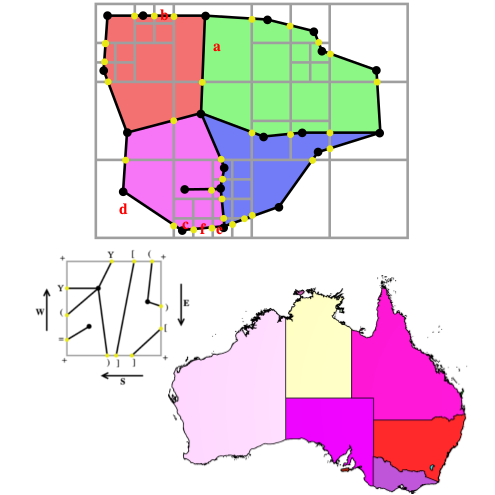
Abstract: A useful example of a Planar Face Complex (PFC) is a connected network of streets, each modeled by a zero-thickness curve. The union of these decomposes the plane into faces that may be topologically complex. The previously proposed rasterized representation of the PFC (abbreviated rPFC) (1) uses a fixed resolution pixel grid, (2) quantizes the geometry of the vertices and edges to pixel-resolution, (3) assumes that no street is contained in a single pixel, and (4) encodes the graph connectivity using a small and fixed number of bits per pixel by decomposing the exact topology into per-pixel descriptors. The hierarchical (irregular) version of the rPFC (abbreviated hPFC) proposed here improved on rPFC in several ways: (1) It uses an adaptively constructed tree to eliminate the “no street in a pixel” constraint of the rPFC, hence making it possible to represent exactly any PFC topology and (2) for PFCs of the models tested, and more generally for models with relatively large empty regions, it reduces the storage cost significantly.

Keywords: Planar polygonal meshes; Irregular representation; Hierarchical representation; Combinatorial maps; Compact representation; Topology preserving rasterization.