Silent MST approximation for tiny memory

Lélia Blin, Swan Dubois, Laurent Feuilloley.

SSS 2020: 22nd International Symposium on Stabilization, Safety, and Security of Distributed Systems, Austin, TX, USA, November 18-21, 2020
doi: 10.1007/978-3-030-64348-5_10

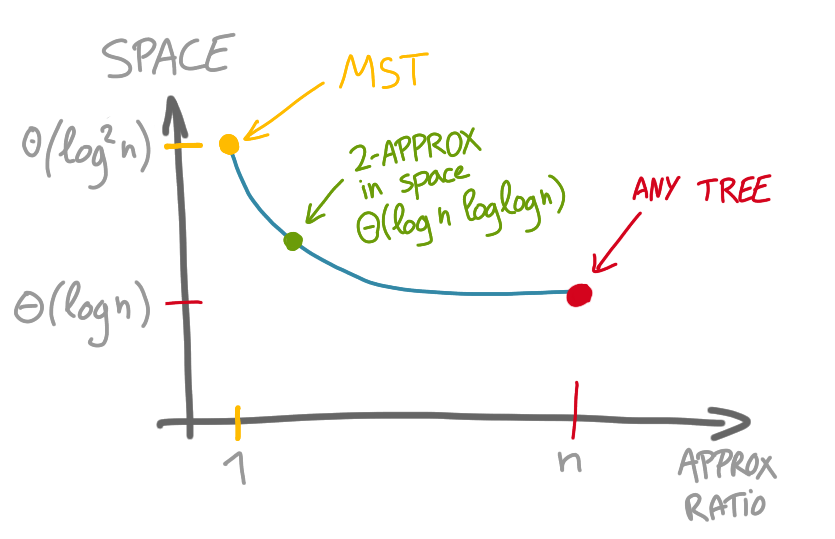
In this paper we show that approximation can help reduce the space used for self-stabilization. In the classic state model, where the nodes of a network communicate by reading the states of their neighbors, an important measure of efficiency is the space: the number of bits used at each node to encode the state. In this model, a classic requirement is that the algorithm has to be silent, that is, after stabilization the states should not change anymore. We design a silent self-stabilizing algorithm for the problem of minimum spanning tree, that has a trade-off between the quality of the solution and the space needed to compute it.

I presented the paper at SSS, in November 2020.

There is a general question that follows from the paper. Basically, what we do is to build the MST and, once it is built, to certify it, to ensure fault-tolerance. This is not classic, as one usually certifies a solution little by little during the computation. I think that this two-step proccess is necessary. I wrote a series of blog post about this, see the first post here.