Locally Optimal Load Balancing

Laurent Feuilloley, Juho Hirvonen Jukka Suomela

DISC 2015: 29th International Symposium on Distributed Computing, Tokyo, Japan, October 2015
doi:10.1007/978-3-662-48653-5_36

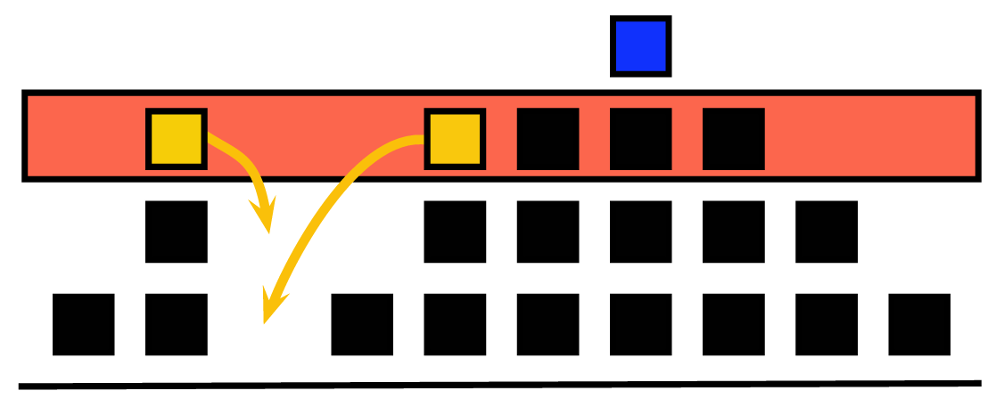
This work studies distributed algorithms for locally optimal load-balancing: We are given a graph of maximum degree $\Delta$, and each node has up to $L$ units of load. The task is to distribute the load more evenly so that the loads of adjacent nodes differ by at most 1.

If the graph is a path ($\Delta = 2$), it is easy to solve the fractional version of the problem in $O(L)$ communication rounds, independently of the number of nodes. We show that this is tight, and we show that it is possible to solve also the discrete version of the problem in $O(L)$ rounds in paths.

For the general case ($\Delta > 2$), we show that fractional load balancing can be solved in $\operatorname{poly}(L,\Delta)$ rounds and discrete load balancing in $f(L,\Delta)$ rounds for some function $f$, independently of the number of nodes.

The talk at DISC was given by Juho Hirvonen. I gave a talk about this paper at the annual meeting of the CNRS's GT COA. I presented the poster at another CNRS event (Journées du GdR IM), and at the seminar of the PHD students of the French Computer Science society (SIF).