Laurent Feuilloley, Pierre Fraigniaud.
SPAA 2015:
27th ACM Symposium on Parallelism in Algorithms and Architectures,
Portland, Oregon, USA, June 13 - 15, 2015
doi:
10.1145/2755573.2755596,
hal:
01247357
In this paper, we carry on investigating the line of research questioning the power of randomization for the design of distributed algorithms.
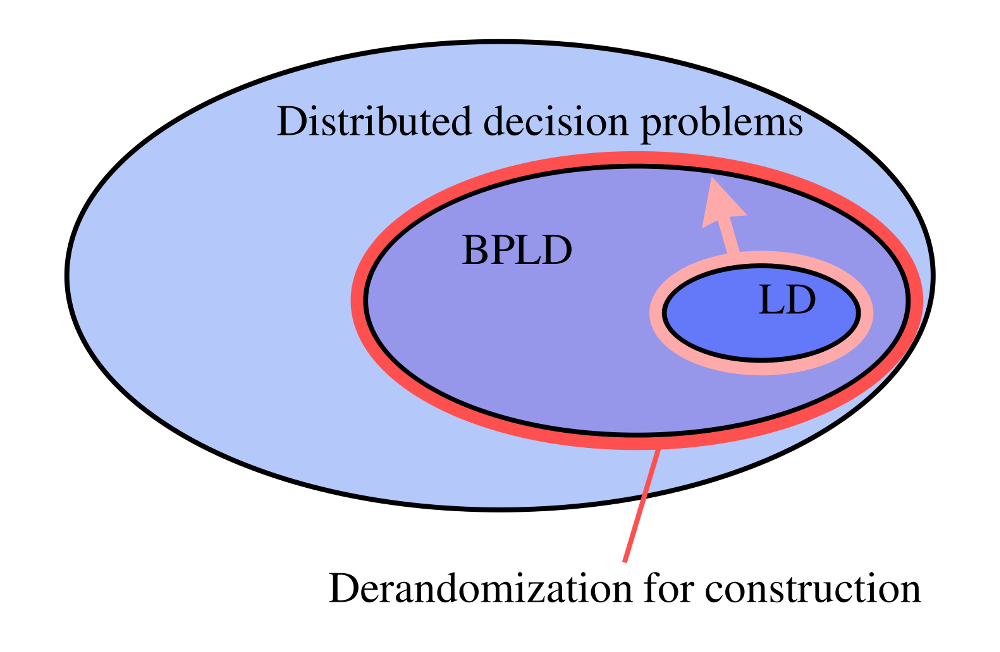
In their seminal paper, Naor and Stockmeyer [STOC 1993] established that, in the context of network computing, in which all nodes execute the same algorithm in parallel, any construction task that can be solved locally by a randomized Monte-Carlo algorithm can also be solved locally by a deterministic algorithm. This result however holds in a specific context. In particular, it holds only for distributed tasks whose solutions can be locally checked by a deterministic algorithm. In this paper, we extend the result of Naor and Stockmeyer to a wider class of tasks. Specifically, we prove that the same derandomization result holds for every task whose solutions can be locally checked using a 2-sided error randomized Monte-Carlo algorithm.
This extension finds applications to, e.g., the design of lower bounds for construction tasks which tolerate that some nodes compute incorrect values. In a nutshell, we show that randomization does not help for solving such resilient tasks.