Independent and Hitting Sets of Rectangles Intersecting a Diagonal Line: Algorithms and Complexity

José R. Correa, Laurent Feuilloley, Pablo Pérez-Lantero, José A. Soto.

Discrete & Computational Geometry
volume 53, pages 344-365 (2015)
doi:10.1007/s00454-014-9661-y

Given a set of n axis-parallel rectangles in the plane, finding a maximum independent set (MIS), a maximum weighted independent set (WMIS), and a minimum hitting set (MHS), are basic problems in computational geometry and combinatorics. They have attracted significant attention since the sixties, when Wegner conjectured that the duality gap, equal to the ratio between the size of MIS and the size of MHS, is always bounded by a universal constant.

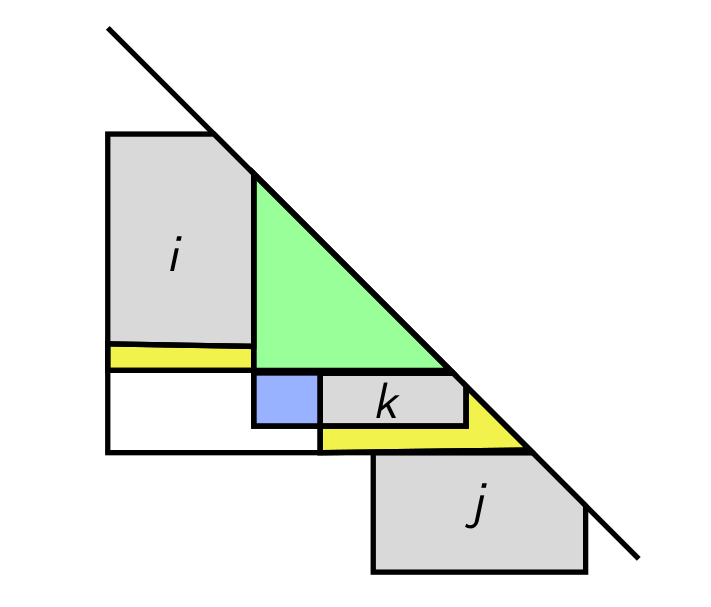
An interesting case is when there exists a diagonal line that intersects each of the given rectangles. Indeed, Chepoi and Felsner recently gave a 6-approximation algorithm for MHS in this setting, and showed that the duality gap is between 3/2 and 6. We consider the same setting and improve upon these results.

First, we derive an $O(n^2)$-time algorithm for the WMIS when, in addition, every pair of intersecting rectangles have a common point below the diagonal. This improves and extends a classic result of Lubiw, and gives a 2-approximation algorithm for WMIS. Second, we show that MIS is NP-hard. Finally, we prove that the duality gap is between 2 and 4. The upper bound, which implies a 4-approximation algorithm for MHS, follows from simple combinatorial arguments, whereas the lower bound represents the best known lower bound on the duality gap, even in the general setting of the rectangles.

The origin of this paper is an internship with José Correa at the Universidad de Chile, in Santiago de Chile. It first appeared at LATIN 2014 (see this page for the conference version, including my slides for the talk).

The main differences in content between the conference and the journal versions are : the proof that MIS on the class of graph we consider is NP-hard (Theorem 5), and the bound on the duality gap for general rectangle families (section 5). A more graph-theoretic part appears in both the conference version, and the arxiv version (section 6) but not in the journal version.